Goal-Driven Flexible
Bayesian Design
Frank Harrell
Department
of Biostatistics
Vanderbilt University School of Medicine
hbiostat.org/bayes/design
Resources:
hbiostat.org/bayes
Clinical Trial Goals &
Challenges
Frequentist
vs. Bayesian Decision Criteria & Operating Characteristics
Frequentist
- Decisions usually made on the basis of \(p\)-values
- OCs: \(\alpha, \beta\)
What may
happen under unknowable assumptions about the treatment effect
generating the data; built upon unobservables
- \(\alpha\) is not the probability
of making an error
- P(making an assertion | unobservable)
- \(\alpha\) does not condition on
the data so is affected by multiple looks
Bayesian
- Decisions based on posterior probability that a clinical assertion
is true
- OCs: correctness of decisions
Comparison
- Freq: Chance of a positive result when there is nothing
vs.
- Bayes: Chance that a positive result turns out to be nothing
- How often a conclusion is correct
- Positive errors: OK by definition if analysis prior = reviewer’s
prior
- Bayesian power affected by prior but dominated by \(N\) and uncertainty in MCID
- Simulations compute P(correct decision) when there is a disagreement
in priors
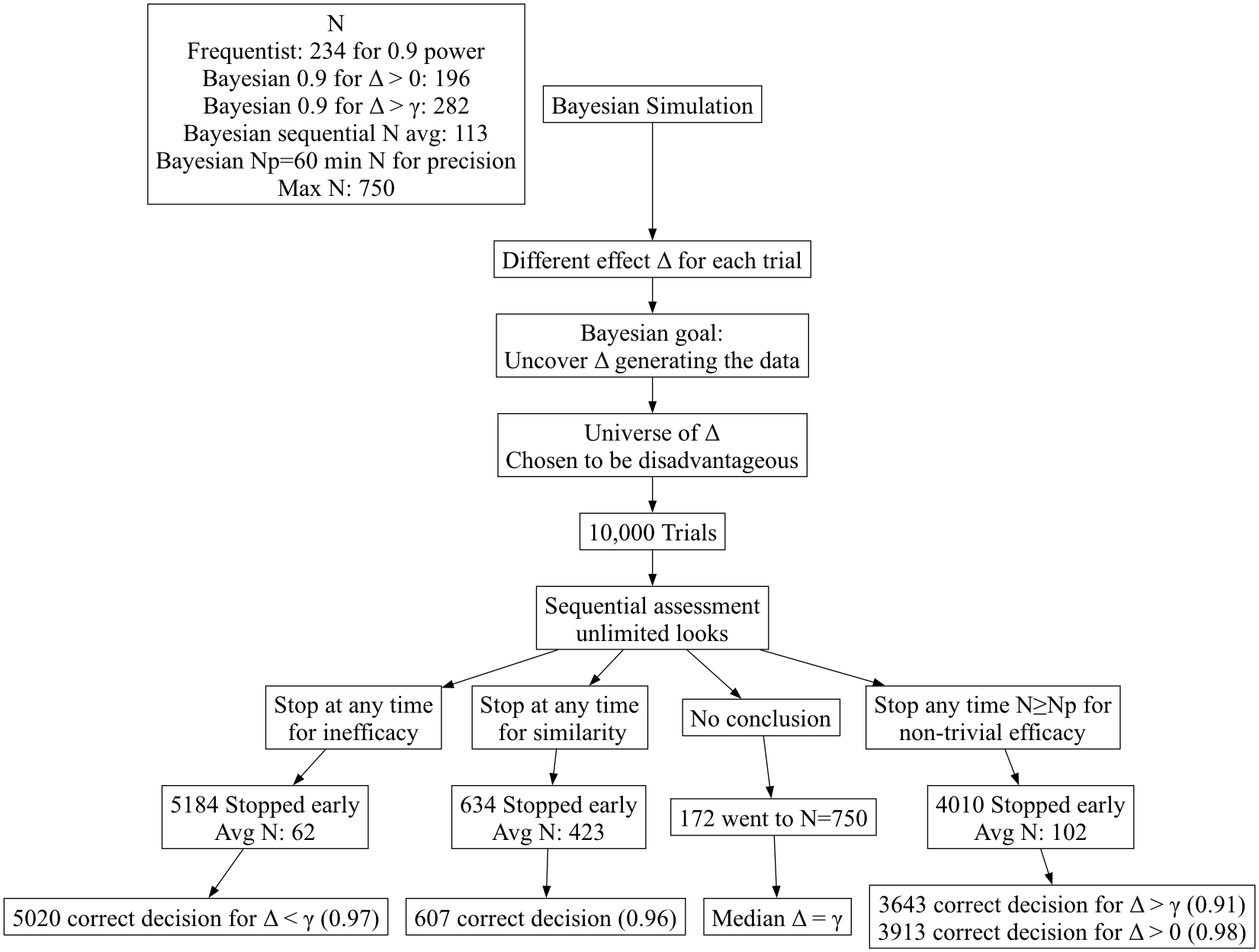
- Simulation setup: simulate 1000 RCTs with 1000 values of \(\Delta\)
- Bayes’ goal: uncover hidden truths behind the data generating
mechanism relying only on observables
- Of those 1000 in which a certain decision was made, count how often
the decision was correct, i.e.,
- Subset the trials to those in which decision \(D\) was made
- Reveal the \(\Delta\) generating
the data in those trials
- Check how often \(\Delta\) was in
the interval corresponding to \(D\)
- Accuracy is a post-data consideration
- Is conditional on the data and the decision, not \(\Delta\)
Simulation
Design Reveals Dramatic Differences Between Paradigms
- Frequentist simulations couldn’t be more different
- and have little to do with data-based decision making
- Simulate 1000 RCTs in which the treatment is irrelevant (\(\Delta=0\))
- Compute a test statistic and \(p\)-value
- Count how often \(p\)<0.05
- Likewise for a single all-too-arbitrary positive treatment
effect
- Multiplicities exist because \(p\)
= P(data extreme) instead of P(\(\Delta\))
more chances for data to be
extreme with more data looks
Extreme
Importance of Goal-Driven Sequential Designs
- Sample size calculations are voodoo
- MCID is gamed and should be recognized as having uncertainty
- Majority of RCTs are equivocal
- Equivocal studies on average could perhaps have been stopped for
futility \(\frac{1}{3}\) of the way
through
- Quiz: if the current treatment effect is harmful, how far along in
trial recruitment can you be for you to still have a good chance of
ultimately showing treatment benefit?
Bayes
Needs No Multiplicity Adjustment for \(\infty\) Data Looks
- Consider a posterior prob (PP) computed at the study end
- Interim analyses use the same construction of PP and same prior so
must also be valid
- Early PP are merely made obsolete by later data
- P(decision error) independent of stopping rules
- Expected sample size is minimized by maximizing # looks
- Demonstration
simulations
Example Bayesian
Sequential Multi-Goal Design
Two-Treatment
Parallel-Group Efficacy Design
Comparing Two Means, Known \(\sigma=1\)
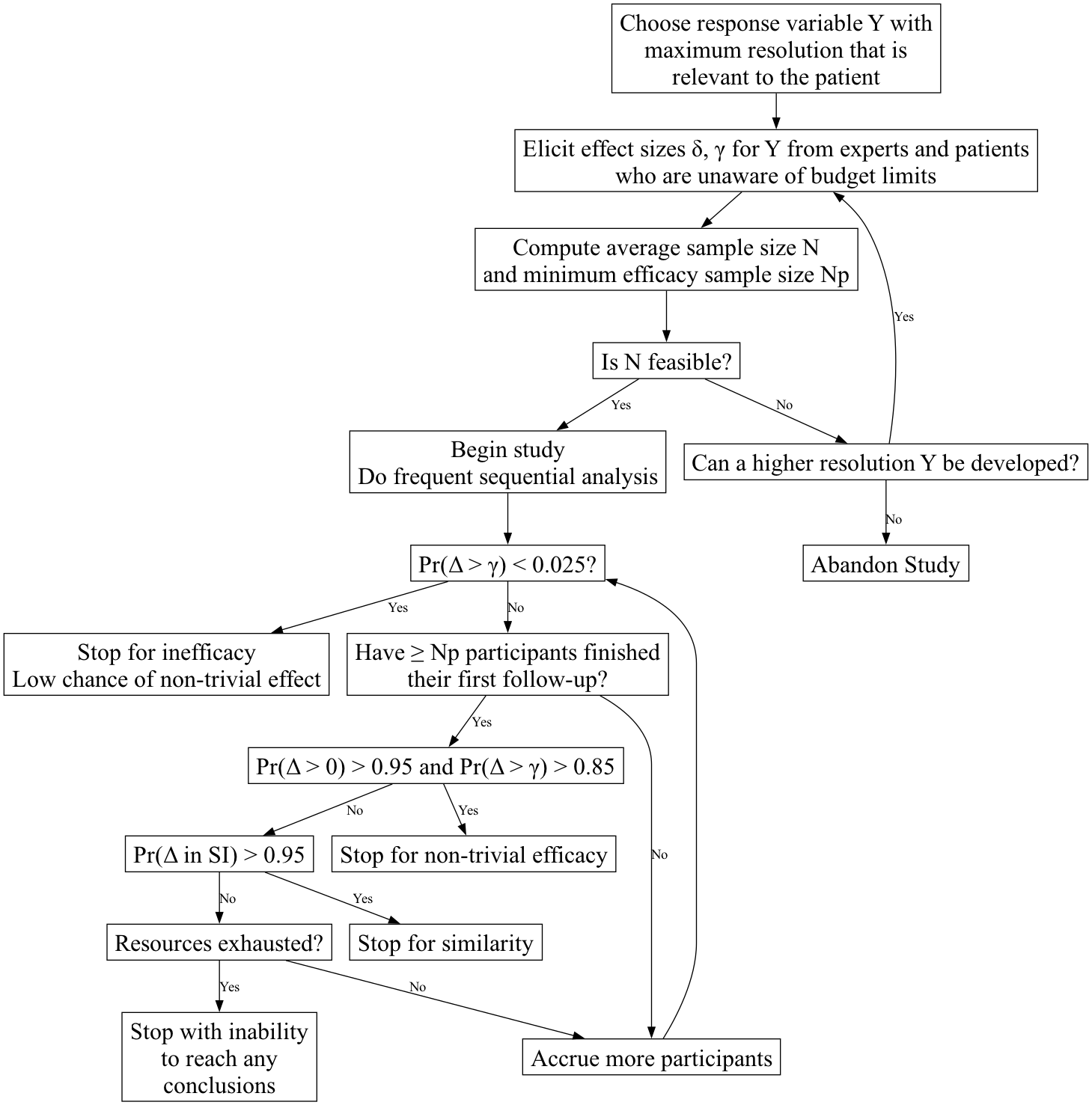
Goals
- Maximize the probability of making the right decision, with 4
decisions possible (efficacy, similarity, inefficacy, not possible to
draw any conclusion with available resources)
- Minimize the probability of an inconclusive result at study end
- Minimize the expected sample size
- Stop as early as possible if there is a very high probability that
the treatment’s effect is trivial or worse, even if the magnitude of the
effect cannot be estimated with any precision
- If stopping early for non-trivial efficacy, make sure that the
sample size provides at least crude precision of the effect estimate
- Do this by not making the first efficacy look until the lowest
sample size for which at least crude precision of the treatment effect
is attained
- Avoid gaming the effect size used in a power calculation
- Recognize that traditional sample sizes are arbitrary and require
too many assumptions
- Recognize that what appears to be a study extension to one person
will appear to be an interim analysis to another who doesn’t need to do
a sample size calculation
- Build clinical significance into the quantification of evidence for
efficacy
Definitions
- \(\Delta\): true treatment effect
being estimated
- \(\delta\): minimum clinically
important \(\Delta\)
- \(\gamma\): minimum detectable
\(\Delta\) (threshold for non-trivial
treatment effect, e.g. \(\frac{1}{3}\delta\))
- SI: similarity interval for \(\Delta\), e.g., \([-\frac{1}{2}\delta,
\frac{1}{2}\delta]\)
- \(N\): average sample size, used
for initial resource planning. This is an estimate of the ultimate
sample size based on assuming \(\Delta =
\delta\). \(N\) is computed to
achieve a Bayesian power of 0.9 for efficacy, i.e., achieving a 0.9
probability at a fixed sample size that the probability of any efficacy
exceeds 0.95 while the probability of non-trivial efficacy exceeds 0.85,
i.e., \(\Pr(\Delta > 0) > 0.95\)
and \(\Pr(\Delta > \gamma) >
0.85\).
- More than one \(N\) can be
computed, e.g., \(N\) such that if
\(\Delta = \gamma\) there is ever a
high probability of stopping for inefficacy
- \(N_p\): minimum sample size for
first efficacy assessment, based on required minimum precision of
estimate of \(\Delta\)
- Probability cutoffs are examples
- This design does not require a separate futility analysis, as
inefficacy subsumes futility
- Below, “higher resolution Y” can come from breaking ties in the
outcome variable (making it more continuous), adding longitudinal
assessments, or extending follow-up
Summary
- Disciplined choices of MCID, outcomes, and trivial effects margins
\(\uparrow\) likelihood of study
success or abandoning futile studies before any $ spent
- It’s best to not have a sample size calculation, especially if
assuming what we’re trying to learn from the study
- Sequential designs can easily have multiple explicit clinical goals
in the Bayesian framework
- They can greatly speed up research
- Bayesian OCs can be very impressive even with conflicting
priors