Code
load(url('https://hbiostat.org/data/repo/gusto.rda'))
setDT(gusto)
gusto <- gusto[tx %in% c('SK', 'tPA'),
.(day30, tx, age, Killip, sysbp, pulse, pmi, miloc, sex)]
gusto[, tx := tx[, drop=TRUE]]
Department of Biostatistics
Vanderbilt University School of Medicine
June 28, 2021
In a randomized clinical trial (RCT) with a binary endpoint Y it is traditional in a frequentist analysis to summarize the estimated treatment effect with an odds ratio (OR), risk ratio (RR), or risk difference (RD, also called absolute risk reduction). For any of these measures there are several forms of estimation:
ORs have some potential to simplify things and can easily be translated into RD, but are not without controversy, and tend to present interpretation problems for some clinical researchers. Marginal adjusted estimates may be robust, but may not accurately estimate RD for either any patient in the RCT or for the clinical population to which RCT results are to be applied, because in effect they assume that the RCT sample is a random sample from the clinical population, something not required and never realized for RCTs.
When Y is a Gaussian continuous response with constant variance, it is possible to reduce the results of an RCT treatment comparison to two numbers: the difference in mean Y and the between-subject covariate-adjusted variance (the latter being used for prediction intervals as opposed to group mean intervals). Things are much different with binary Y. Among other things, the variance of Y is a function of the mean of Y (P(Y=1)), and model misspecification will alter all of the coefficients in a logistic model. A rich discussion and debate about effect measures, especially ORs, has been held on datamethods.org. At the heart of the debate, as well stated by Sander Greenland, are problems caused by one attempting to reduce a treatment effect to a single number such as an OR or RD.
For individual patient decision making, when narrowing the focus to efficacy alone, the best information to present to the patient is the estimated individualized risk of the bad outcome separately under all treatment alternatives. That is because patients tend to think in terms of absolute risk, and differences in risks don’t tell the whole story. A RD often means different things to patients depending on whether the base risk is very small, in the middle, or very large. For this article, results for all patients and not just any one patient are presented, and the picture is simplified to estimation of RD and not its two component probabilities. But one full-information graphical representation of the component probabilities is also presented.
I propose that the entire distribution of RD from the trial be presented rather than putting so much emphasis on single-number summaries. Some single-number summaries are still needed, however, such as
The adjusted marginal RD is the mean over all estimated RDs. As exemplified in the GUSTO-I study, the mean RD may not be representative due to outliers, i.e., the mean RD may be dominated by a minority of high-risk patients. Median RD is more representative of the mortality reduction patients may achieve in this study.
The covariate-adjusted logistic regression model does not have to be perfect for estimates to be valid (either ORs or RDs). This model is recommended for obtaining the primary statistical evidence for any efficacy, by testing that the treatment OR is 1.0. In the absence of treatment \(\times\) baseline covariate interactions, there is only one p-value. What happens when our RCT presentation involves a distribution of 10,000 RDs for 10,000 patients? There is still only one p-value, because under the model assumptions the risk difference is zero if and only if OR=1.0.
When one moves from testing whether there is any efficacy vs. whether there is absolute efficacy beyond a certain level, e.g., RD > 0.02, the statistical evidence will vary depending not only on the RD cutoff but also on how high risk is the patient. For example, Bayesian posterior probabilities that RD > d are functions of d and baseline covariates.
As a side note, from an RD perspective, the treatment benefit that a patient gets from being high risk is indistinguishable from the benefit she gets due to a treatment \(\times\) baseline covariate interaction. But it does matter for quantifying statistical evidence.
For the remainder of the article I concentrate on summarizing trials using the entire RD distribution.
The 41,000 patient GUSTO-I study has been a gold mine for predictive modeling and efficacy exploration, spawning many excellent statistical re-analyses. The study goal was to provide evidence for whether or not t-PA lowered mortality over streptokinase (SK) for patients with acute myocardial infarction. Overall proportion of deaths at 30d was 0.07. I analyze a subset of 30,510 patients to compare the accelerated dosing of t-PA with streptokinase. Descriptive statistics may be found here.
Extensive analyses of the dataset have found no evidence for treatment interactions in this dataset, and that an additive (on the logit scale) binary logistic model with flexible modeling of continuous variables provides an excellent data fit.
Fit the full covariate-adjusted model.
Logistic Regression Model
lrm(formula = day30 ~ tx + rcs(age, 4) + Killip + pmin(sysbp,
120) + lsp(pulse, 50) + pmi + miloc + sex, data = gusto)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 30510 | LR χ2 3038.55 | R2 0.239 | C 0.818 |
| 0 28382 | d.f. 14 | R214,30510 0.094 | Dxy 0.636 |
| 1 2128 | Pr(>χ2) <0.0001 | R214,5938.7 0.399 | γ 0.637 |
| max |∂log L/∂β| 3×10-11 | Brier 0.055 | τa 0.083 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| Intercept | -0.4294 | 1.0148 | -0.42 | 0.6722 |
| tx=tPA | -0.2071 | 0.0530 | -3.91 | <0.0001 |
| age | 0.0231 | 0.0132 | 1.76 | 0.0792 |
| age' | 0.0928 | 0.0282 | 3.29 | 0.0010 |
| age'' | -0.2835 | 0.1011 | -2.80 | 0.0050 |
| Killip=II | 0.6155 | 0.0591 | 10.41 | <0.0001 |
| Killip=III | 1.1602 | 0.1215 | 9.55 | <0.0001 |
| Killip=IV | 1.9241 | 0.1626 | 11.84 | <0.0001 |
| sysbp | -0.0391 | 0.0019 | -20.23 | <0.0001 |
| pulse | -0.0240 | 0.0160 | -1.50 | 0.1331 |
| pulse' | 0.0427 | 0.0163 | 2.62 | 0.0087 |
| pmi=yes | 0.4834 | 0.0567 | 8.53 | <0.0001 |
| miloc=Other | 0.2818 | 0.1348 | 2.09 | 0.0366 |
| miloc=Anterior | 0.5484 | 0.0513 | 10.69 | <0.0001 |
| sex=female | 0.2886 | 0.0519 | 5.56 | <0.0001 |
Wald Statistics for day30 |
|||
| χ2 | d.f. | P | |
|---|---|---|---|
| tx | 15.27 | 1 | <0.0001 |
| age | 921.01 | 3 | <0.0001 |
| Nonlinear | 16.08 | 2 | 0.0003 |
| Killip | 280.96 | 3 | <0.0001 |
| sysbp | 409.43 | 1 | <0.0001 |
| pulse | 219.96 | 2 | <0.0001 |
| Nonlinear | 6.89 | 1 | 0.0087 |
| pmi | 72.81 | 1 | <0.0001 |
| miloc | 114.29 | 2 | <0.0001 |
| sex | 30.88 | 1 | <0.0001 |
| TOTAL NONLINEAR | 23.15 | 3 | <0.0001 |
| TOTAL | 2425.03 | 14 | <0.0001 |
The t-PA:SK odds ratio is 0.81. But let’s present richer results. Estimate the distribution of SK - t-PA risk differences from the above full covariate-adjusted model. But first show the full information needed for medical decision making: the estimated risks for individual patients under both treatment alternatives. One can readily see risk magnification in the absolute risk reduction as baseline risk increases. The points are all on a line because the logistic model allowed for no interactions with treatment (and no interactions were needed).
prisk <- function(fit) {
d <- copy(gusto) # otherwise next command will make data.table change the original dataset
d[, tx := 'SK']
p1 <- plogis(predict(fit, d))
d[, tx := 'tPA']
p2 <- plogis(predict(fit, d))
list(p1=p1, p2=p2)
}
pr <- prisk(f)
with(pr, ggfreqScatter(p1, p2, bins=1000) +
geom_abline(intercept=0, slope=1) +
xlab('Risk of Mortality for SK') +
ylab('Risk of Mortality for t-PA'))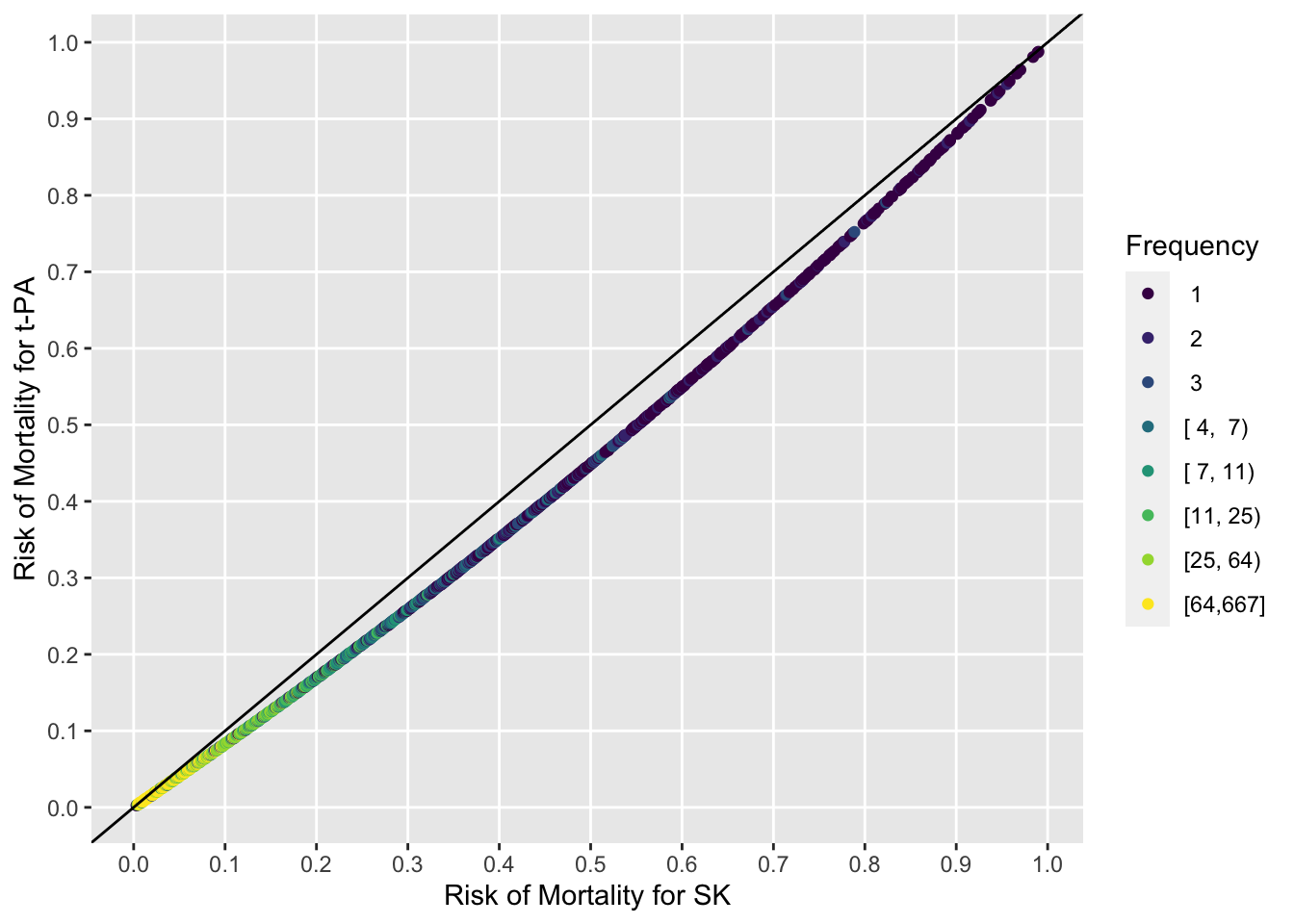
xl <- 'SK - t-PA Risk Difference'
d <- with(pr, p1 - p2)
hist(d, nclass=100, prob=TRUE, xlab=xl, main='')
lines(density(d, adj=0.4))
mmed <- function(x, pl=TRUE) {
mn <- mean(x)
md <- median(x)
if(pl) abline(v=c(mn, md), col=c('red', 'blue'))
round(c('Mean risk difference'=mean(x), 'Median RD'=median(x)), 4)
}
mmed(d)Mean risk difference Median RD
0.0111 0.0067 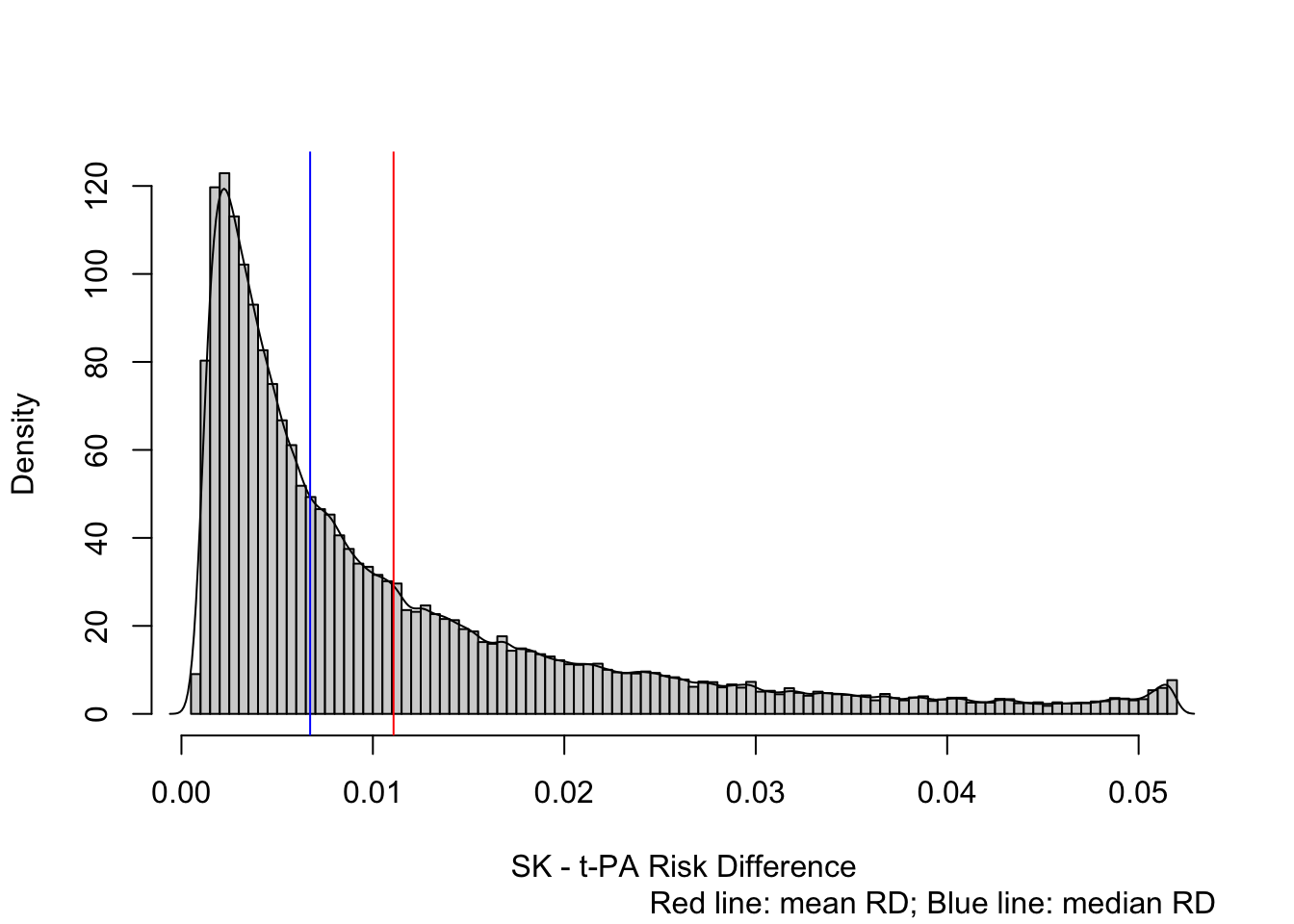
This graph provides a much fuller picture than an OR or than the blue or red vertical lines (median and mean RD). Clinicians can readily see that most patients are lower risk and receive little absolute benefit form t-PA, while a minority of very high-risk patients can receive almost an absolute 0.05 risk reduction. But the previous graph shows even more.
We can never make the data better than they are. We would like to know the RD distribution for a model that adjusts for all prognostic factors, but it is not possible to know or to measure all such factors. In the spirit of SIMEX (simulation-extrapolation) which is used to correct for measurement error when estimating parameters, we can make things worse than they are and study how things vary. Use a fast backwards stepdown procedure to rank covariates by their apparent predictive importance, then remove covariates one-at-a-time so that only the apparently most important variable (age) remains. For each model show the distribution of RDs computed from it. Keep treatment in all models though.
Deleted Chi-Sq d.f. P Residual d.f. P AIC
tx 15.27 1 1e-04 15.27 1 1e-04 13.27
sex 30.92 1 0e+00 46.19 2 0e+00 42.19
pmi 63.89 1 0e+00 110.09 3 0e+00 104.09
miloc 105.93 2 0e+00 216.02 5 0e+00 206.02
pulse 286.28 2 0e+00 502.30 7 0e+00 488.30
sysbp 292.69 1 0e+00 794.98 8 0e+00 778.98
Killip 633.77 3 0e+00 1428.75 11 0e+00 1406.75
age 996.28 3 0e+00 2425.03 14 0e+00 2397.03
Approximate Estimates after Deleting Factors
Coef S.E. Wald Z P
[1,] -2.101 0.02446 -85.89 0
Factors in Final Model
Noneforms <- list('full' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + pmi + miloc + sex,
'-sex' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + pmi + miloc,
'-pmi' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + miloc,
'-miloc' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50),
'-pulse' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120),
'-sysbp' =day30 ~ tx + rcs(age,4) + Killip,
'-Killip'=day30 ~ tx + rcs(age,4))
z <- u <- NULL; i <- 0; nm <- names(forms)
for(form in forms) {
i <- i + 1
f <- lrm(form, data=gusto, maxit=30)
d <- with(prisk(f), p1 - p2)
z <- rbind(z, data.frame(model=nm[i], d=d))
u <- rbind(u, data.frame(model=nm[i], what=c('mean', 'median'),
stat=c(mean(d), median(d))))
if(i > 1) cat('Mean |difference in RD| compared to previous model:',
round(mean(abs(d - dprev)), 4), '\n')
dprev <- d
}Mean |difference in RD| compared to previous model: 0.001
Mean |difference in RD| compared to previous model: 0.0011
Mean |difference in RD| compared to previous model: 0.002
Mean |difference in RD| compared to previous model: 0.0025
Mean |difference in RD| compared to previous model: 0.0024
Mean |difference in RD| compared to previous model: 0.0028 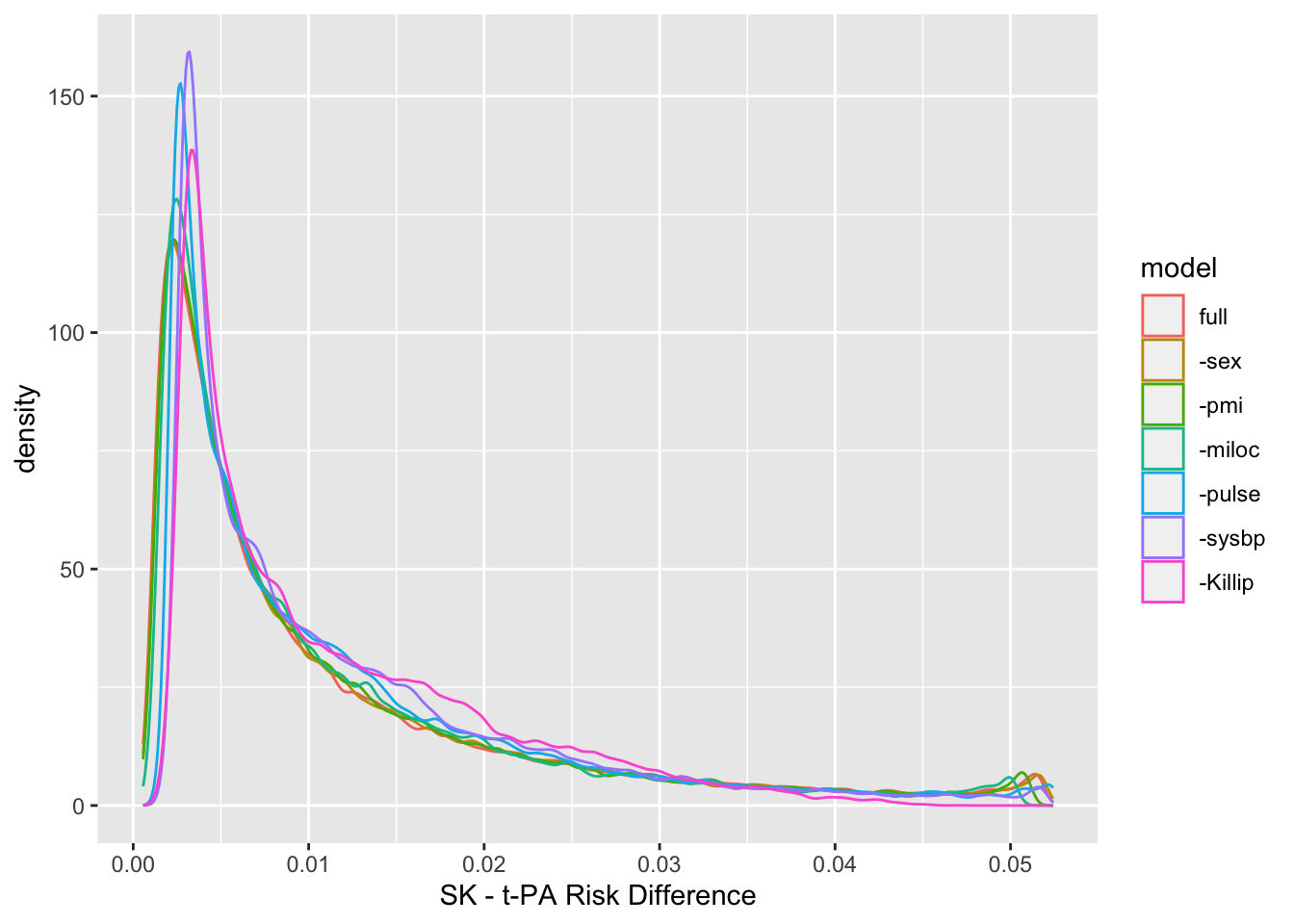
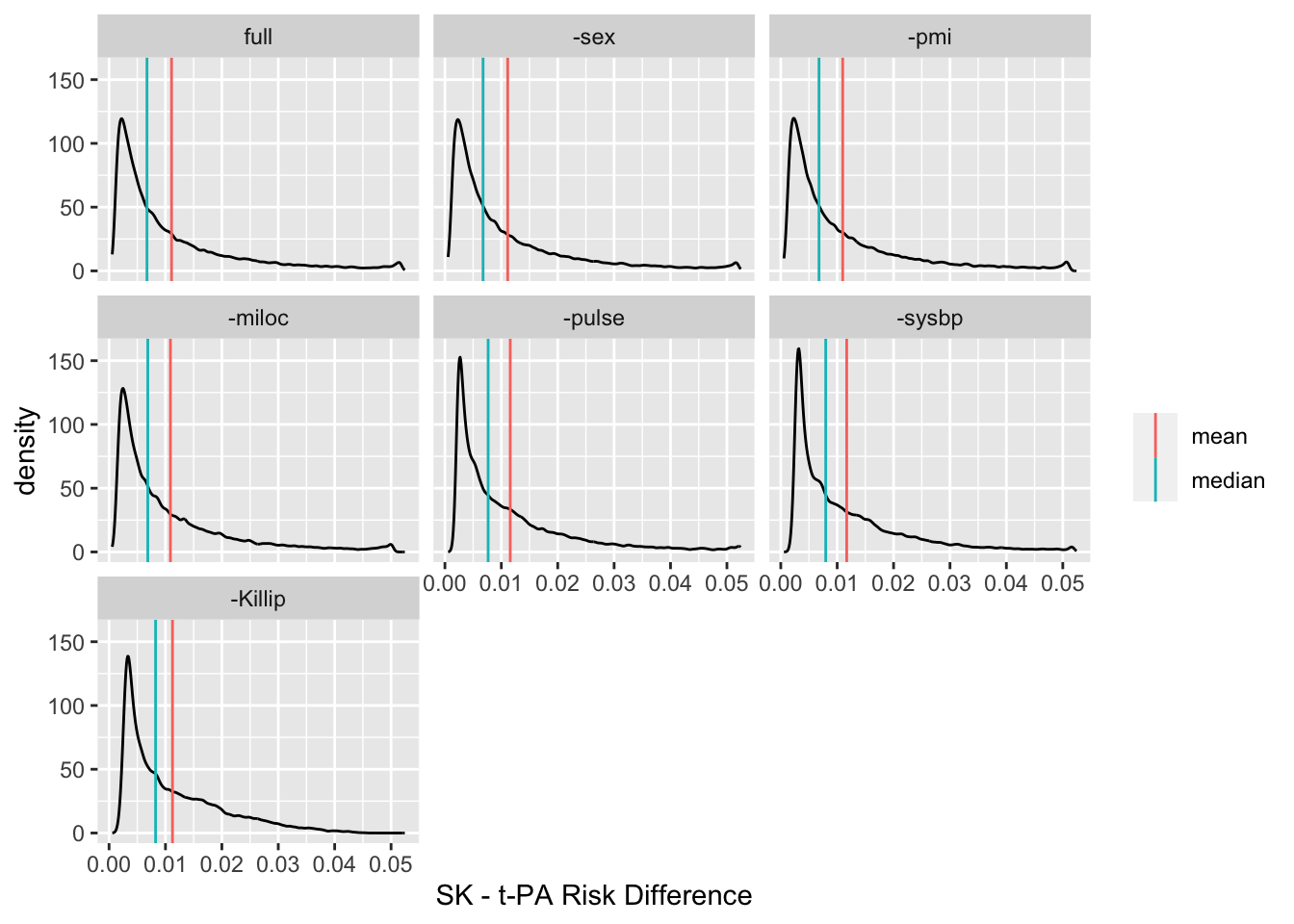
The final model (labeled -Killip) contains only age and treatment. The risk difference distribution is fairly stable over the various models.
The never-ending discussion about the choice of effect measures when Y is binary is best resolved by avoiding the oversimplifications that are required to make such choices. The proposed summarization of the main trial result is more clinically interpretable, more consistent with individual patient decision making, and embraces rather than hides outcome heterogeneity in the RD distribution. See this for some related discussions.
---
title: Avoiding One-Number Summaries of Treatment Effects for RCTs with Binary Outcomes
author:
- name: Frank Harrell
url: https://hbiostat.org
affiliation: Department of Biostatistics<br>Vanderbilt University School of Medicine
date: '2021-06-28'
modified: '2023-04-04'
categories: [2021, generalizability, RCT, regression]
description: "This article presents an argument that for RCTs with a binary outcome the primary result should be a distribution and not any single number summary. The GUSTO-I study is used to exemplify risk difference distributions."
---
```{r setup, include=FALSE}
require(rms)
require(knitr)
require(ggplot2)
require(data.table)
# knitrSet(lang='blogdown')
options(prType='html')
```
<style>
.table {
width: 50%;
}
</style>
# Background
In a randomized clinical trial (RCT) with a binary endpoint Y it is traditional in a frequentist analysis to summarize the estimated treatment effect with an odds ratio (OR), risk ratio (RR), or risk difference (RD, also called absolute risk reduction). For any of these measures there are several forms of estimation: [[Comments](https://hbiostat.org/comment.html)]{.aside}
* simple crude marginal estimates
* covariate-conditional estimates (the usual covariate adjustment approach using a single stage regression analysis)
* marginal adjusted estimate (average personalized RD using a two-stage approach)
ORs have some potential to simplify things and can easily be [translated into RD](/post/ehrs-rcts/), but are not without controversy, and tend to present interpretation problems for some clinical researchers. Marginal adjusted estimates may be robust, but [may not accurately estimate RD](/post/robcov) for either any patient in the RCT or for the clinical population to which RCT results are to be applied, because in effect they assume that the RCT sample is a random sample from the clinical population, something not required and never realized for RCTs.
When Y is a Gaussian continuous response with constant variance, it is possible to reduce the results of an RCT treatment comparison to two numbers: the difference in mean Y and the between-subject covariate-adjusted variance (the latter being used for prediction intervals as opposed to group mean intervals). Things are [much different](https://hbiostat.org/bbr/md/ancova.html) with binary Y. Among other things, the variance of Y is a function of the mean of Y (P(Y=1)), and model misspecification will alter all of the coefficients in a logistic model. A rich discussion and debate about effect measures, especially ORs, has been held on [datamethods.org](https://discourse.datamethods.org/t/should-one-derive-risk-difference-from-the-odds-ratio). At the heart of the debate, as well stated by Sander Greenland, are problems caused by one attempting to reduce a treatment effect to a single number such as an OR or RD.
For individual patient decision making, when narrowing the focus to efficacy alone, the best information to present to the patient is the estimated individualized risk of the bad outcome separately under all treatment alternatives. That is because patients tend to think in terms of absolute risk, and differences in risks don't tell the whole story. A RD often means different things to patients depending on whether the base risk is very small, in the middle, or very large. For this article, results for all patients and not just any one patient are presented, and the picture is simplified to estimation of RD and not its two component probabilities. But one full-information graphical representation of the component probabilities is also presented.
# Statistical Evidence for Efficacy
I propose that the entire distribution of RD from the trial be presented rather than putting so much emphasis on single-number summaries. Some single-number summaries are still needed, however, such as
* covariate-adjusted OR
* adjusted marginal RD (mean personalized predicted risk as if all patients were on treatment A minus mean predicted risk as if all patients were on treatment B)
* median RD
The adjusted marginal RD is the mean over all estimated RDs. As exemplified in the GUSTO-I study, the [mean RD may not be representative due to outliers](https://hbiostat.org/bbr/md/ancova.html), i.e., the mean RD may be dominated by a minority of high-risk patients. Median RD is more representative of the mortality reduction patients may achieve in this study.
The covariate-adjusted logistic regression model [does not have to be perfect](/post/robcov) for estimates to be valid (either ORs or RDs). This model is recommended for obtaining the primary statistical evidence for _any_ efficacy, by testing that the treatment OR is 1.0. In the absence of treatment $\times$ baseline covariate interactions, there is only one p-value. What happens when our RCT presentation involves a distribution of 10,000 RDs for 10,000 patients? There is still only one p-value, because under the model assumptions the risk difference is zero if and only if OR=1.0.
When one moves from testing whether there is _any_ efficacy vs. whether there is absolute efficacy beyond a certain level, e.g., RD > 0.02, the statistical evidence will vary depending not only on the RD cutoff but also on how high risk is the patient. For example, Bayesian posterior probabilities that RD > d are functions of d and baseline covariates.
As a side note, from an RD perspective, the treatment benefit that a patient gets from being high risk is indistinguishable from the benefit she gets due to a treatment $\times$ baseline covariate interaction. But it does matter for quantifying statistical evidence.
For the remainder of the article I concentrate on summarizing trials using the entire RD distribution.
# GUSTO-I
The 41,000 patient [GUSTO-I study](https://www.nejm.org/doi/full/10.1056/NEJM199309023291001) has been a gold mine for predictive modeling and efficacy exploration, spawning many excellent [statistical re-analyses](/post/covadj). The study goal was to provide evidence for whether or not t-PA lowered mortality over streptokinase (SK) for patients with acute myocardial infarction. Overall proportion of deaths at 30d was 0.07. I analyze a subset of 30,510 patients to compare the accelerated dosing of t-PA with streptokinase. Descriptive statistics may be found [here](/post/covadj).
[Extensive analyses](/post/varyor) of the dataset have found no evidence for treatment interactions in this dataset, and that an additive (on the logit scale) binary logistic model with flexible modeling of continuous variables provides an excellent data fit.
```{r gusto}
load(url('https://hbiostat.org/data/repo/gusto.rda'))
setDT(gusto)
gusto <- gusto[tx %in% c('SK', 'tPA'),
.(day30, tx, age, Killip, sysbp, pulse, pmi, miloc, sex)]
gusto[, tx := tx[, drop=TRUE]]
```
Fit the full covariate-adjusted model.
```{r model,results='asis'}
f <- lrm(day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) +
pmi + miloc + sex, data=gusto)
f
anova(f)
```
# Distribution of RDs in GUSTO-I
The t-PA:SK odds ratio is `r round(exp(coef(f)['tx=tPA']), 2)`. But let's present richer results. Estimate the distribution of SK - t-PA risk differences from the above full covariate-adjusted model. But first show the full information needed for medical decision making: the estimated risks for individual patients under both treatment alternatives. One can readily see risk magnification in the absolute risk reduction as baseline risk increases. The points are all on a line because the logistic model allowed for no interactions with treatment (and no interactions were needed).
```{r rd1,bot=1}
prisk <- function(fit) {
d <- copy(gusto) # otherwise next command will make data.table change the original dataset
d[, tx := 'SK']
p1 <- plogis(predict(fit, d))
d[, tx := 'tPA']
p2 <- plogis(predict(fit, d))
list(p1=p1, p2=p2)
}
pr <- prisk(f)
with(pr, ggfreqScatter(p1, p2, bins=1000) +
geom_abline(intercept=0, slope=1) +
xlab('Risk of Mortality for SK') +
ylab('Risk of Mortality for t-PA'))
xl <- 'SK - t-PA Risk Difference'
d <- with(pr, p1 - p2)
hist(d, nclass=100, prob=TRUE, xlab=xl, main='')
lines(density(d, adj=0.4))
mmed <- function(x, pl=TRUE) {
mn <- mean(x)
md <- median(x)
if(pl) abline(v=c(mn, md), col=c('red', 'blue'))
round(c('Mean risk difference'=mean(x), 'Median RD'=median(x)), 4)
}
mmed(d)
title(sub='Red line: mean RD; Blue line: median RD', adj=1)
```
This graph provides a much fuller picture than an OR or than the blue or red vertical lines (median and mean RD). Clinicians can readily see that most patients are lower risk and receive little absolute benefit form t-PA, while a minority of very high-risk patients can receive almost an absolute 0.05 risk reduction. But the previous graph shows even more.
# RD Distribution Under Different Models
We can never make the data better than they are. We would like to know the RD distribution for a model that adjusts for all prognostic factors, but it is not possible to know or to measure all such factors. In the spirit of [SIMEX](https://www.stata.com/merror/simex.pdf) (simulation-extrapolation) which is used to correct for measurement error when estimating parameters, we can make things worse than they are and study how things vary. Use a fast backwards stepdown procedure to rank covariates by their apparent predictive importance, then remove covariates one-at-a-time so that only the apparently most important variable (age) remains. For each model show the distribution of RDs computed from it. Keep treatment in all models though.
```{r bw}
fastbw(f, aics=100000)
forms <- list('full' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + pmi + miloc + sex,
'-sex' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + pmi + miloc,
'-pmi' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50) + miloc,
'-miloc' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120) + lsp(pulse, 50),
'-pulse' =day30 ~ tx + rcs(age,4) + Killip + pmin(sysbp, 120),
'-sysbp' =day30 ~ tx + rcs(age,4) + Killip,
'-Killip'=day30 ~ tx + rcs(age,4))
z <- u <- NULL; i <- 0; nm <- names(forms)
for(form in forms) {
i <- i + 1
f <- lrm(form, data=gusto, maxit=30)
d <- with(prisk(f), p1 - p2)
z <- rbind(z, data.frame(model=nm[i], d=d))
u <- rbind(u, data.frame(model=nm[i], what=c('mean', 'median'),
stat=c(mean(d), median(d))))
if(i > 1) cat('Mean |difference in RD| compared to previous model:',
round(mean(abs(d - dprev)), 4), '\n')
dprev <- d
}
z$model <- factor(z$model, levels=nm)
u$model <- factor(u$model, levels=nm)
ggplot(z, aes(x=d, color=model)) + geom_density(adjust=0.4) + xlab(xl)
ggplot(z, aes(x=d)) + geom_density(adjust=0.4) + geom_vline(data=u, aes(xintercept=stat, color=what)) +
facet_wrap(~ model) + xlab(xl) + theme(legend.title=element_blank())
```
The final model (labeled `-Killip`) contains only age and treatment. The risk difference distribution is fairly stable over the various models.
# Summary
The never-ending discussion about the choice of effect measures when Y is binary is best resolved by avoiding the oversimplifications that are required to make such choices. The proposed summarization of the main trial result is more clinically interpretable, more consistent with individual patient decision making, and embraces rather than hides outcome heterogeneity in the RD distribution. See [this](/post/robcov) for some related discussions.
# Further Reading
* [Unit-level contrasts in logistic regressions](https://vincentarelbundock.github.io/marginaleffects/articles/logit.html) by Arthur Aluquerque, edited by Vincent Arel-Bundock
* [Limitations of Applying Summary Results of Clinical Trials to Individual Patients](https://jamanetwork.com/journals/jama/article-abstract/208701) by David Kent and Rod Hayward
* [Risk ratio, odds ratio, risk difference... Which causal measure is easier to generalize?](https://arxiv.org/abs/2303.16008) by Colnet, Josse, Varoquaux, Scornet
* [The odds ratio is "portable" across baseline risk but not the relative risk: Time to do away with the log link in binomial regression](https://www.jclinepi.com/article/S0895-4356(21)00241-9/fulltext) by Doi, Furuya-Kanamori, Xu, Chivese, Lin, Musa, Hindy, Thalib, Harrell
* [Should one derive risk difference from the odds ratio?](https://discourse.datamethods.org/t/should-one-derive-risk-difference-from-the-odds-ratio)