9 Descriptive Statistics

flowchart LR
des[describe Function] --> ss[Statistical Summary] & dsh[Spike Histogram]
cat[Categorical Variables] --> dot[Frequency Dot Charts]
con[Continuous Variables] --> sh[Spike Histograms] & ebp[Extended Box Plots] & ecdf[Empirical Cumulative Distributions]
lon[Longitudinal Data] --> sg[Spaghetti Graphs] & rc[Representative Curves] & ol[Ordinal Transitions<br>and States] & mlong[Multiple<br>Longitudinal<br>Variables]
ev[Events] --> mc[Multi-category Event Charts] & tl[Timelines]
rel[Relationships] --> cm[Graphical Correlation Matrix] & vc[Variable Clustering]

9.1 Simple Descriptive Statistics

The Hmisc describe function is my main tool for getting initial descriptive statistics and quality controlling the data in a univariate fashion. Here is an example. The Info index is a measure of the information content in a numeric variable relative to the information in a continuous numeric variable with no ties. A very low value of Info will occur when a highly imbalanced variable is binary. Clicking on Glossary on the right will pop up a browser window with a more in-depth glossary of terms used in Hmisc package output. It links to hbiostat.org/R/glossary.html which you can link from your reports that use Hmisc.

Info comes from the approximate formula for the variance of a log odds ratio for a proportional odds model/Wilcoxon test, due to Whitehead.
Glossary

Gmd in the output stands for Gini’s mean difference—the mean absolute difference over all possible pairs of different observations. It is a very interpretable measure of dispersion that is more robust than the standard deviation.

require(Hmisc)
options(prType='html')   # have certain Hmisc functions render in html
require(qreport)
hookaddcap()   # make knitr call a function at the end of each chunk
               # to try to automatically add to list of figure

getHdata(stressEcho)
d <- stressEcho

describe Output

# The callout was typed manually; could have run
#  makecnote(~ describe(d), wide=TRUE)
w <- describe(d)
w

d Descriptives

d

31 Variables 558 Observations

bhr: Basal heart rate bpm

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	69	0.999	75.29	74.5	16.57	54.0	58.0	64.0	74.0	84.0	95.3	102.0

lowest : 42 44 45 46 47 , highest: 108 115 116 127 210

basebp: Basal blood pressure mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	94	0.998	135.3	134.5	23.35	104.0	110.0	120.0	133.0	150.0	162.3	170.1

lowest : 85 88 90 97 98 , highest: 192 194 195 201 203

basedp: Basal Double Product bhr*basebp bpm*mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	441	1	10181	10016	2813	6607	7200	8400	9792	11663	13610	14770

lowest : 5000 5220 5280 5400 5460 , highest: 17604 17710 17748 21082 27300

pkhr: Peak heart rate mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	105	1	120.6	121	25.36	81.85	90.70	106.25	122.00	135.00	147.00	155.15

lowest : 52 61 62 63 66 , highest: 170 171 176 182 210

sbp: Systolic blood pressure mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	142	1	146.9	145	40.72	96	102	120	141	170	200	210

lowest : 40 60 70 79 80 , highest: 240 250 274 283 309

dp: Double product pkhr*sbp bpm*mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	508	1	17634	17339	5765	10256	11341	14033	17060	20644	24536	26637

lowest : 5100 5940 7490 8100 8360 , highest: 32518 33400 33840 38205 45114

dose: Dose of dobutamine given mg

n	missing	distinct	Info	Mean	pMedian	Gmd
558	0	7	0.84	33.75	35	8.334

 Value         10    15    20    25    30    35    40
 Frequency      2    28    47    56    64    61   300
 Proportion 0.004 0.050 0.084 0.100 0.115 0.109 0.538

For the frequency table, variable is rounded to the nearest 0

maxhr: Maximum heart rate bpm

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	103	1	119.4	119.5	24.64	82.0	91.0	104.2	120.0	133.0	146.0	154.1

lowest : 58 62 63 66 67 , highest: 170 171 176 182 200

pctMphr: Percent maximum predicted heart rate achieved %

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	78	0.999	78.57	78.5	16.86	53	60	69	78	88	97	104

lowest : 38 39 40 41 42 , highest: 116 117 126 132 133

mbp: Maximum blood pressure mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	132	0.999	156	154	35.03	110.0	120.0	133.2	150.0	175.8	200.0	211.1

lowest : 84 90 92 93 96 , highest: 240 250 274 283 309

dpmaxdo: Double product on max dobutamine dose bpm*mmHg

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	484	1	18550	18267	5385	11346	12865	15260	18118	21239	24893	27477

lowest : 7130 8100 8360 9240 9280 , highest: 32518 33400 33840 38205 45114

dobdose: Dobutamine dose at max double product mg

n	missing	distinct	Info	Mean	pMedian	Gmd
558	0	8	0.941	30.24	30	10.55

 Value          5    10    15    20    25    30    35    40
 Frequency      7     7    55    73    71    78    62   205
 Proportion 0.013 0.013 0.099 0.131 0.127 0.140 0.111 0.367

For the frequency table, variable is rounded to the nearest 0

age: Age years

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	62	0.999	67.34	68	13.41	46.85	51.00	60.00	69.00	75.00	82.00	85.00

lowest : 26 28 29 30 33 , highest: 89 90 91 92 93

gender

n	missing	distinct
558	0	2

 Value        male female
 Frequency     220    338
 Proportion  0.394  0.606

baseEF: Baseline cardiac ejection fraction %

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	54	0.994	55.6	57	10.71	32	40	52	57	62	65	66

lowest : 20 21 22 23 25 , highest: 74 75 77 79 83

dobEF: Ejection fraction on dobutamine %

n	missing	distinct	Info	Mean	pMedian	Gmd	.05	.10	.25	.50	.75	.90	.95
558	0	60	0.992	65.24	67	12.38	40.0	49.7	62.0	67.0	73.0	76.0	80.0

lowest : 23 25 26 27 28 , highest: 86 87 89 90 94

chestpain: Chest pain

n	missing	distinct	Info	Sum	Mean
558	0	2	0.64	172	0.3082

restwma: Resting wall motion abnormality on echocardiogram

n	missing	distinct	Info	Sum	Mean
558	0	2	0.745	257	0.4606

posSE: Positive stress echocardiogram

n	missing	distinct	Info	Sum	Mean
558	0	2	0.553	136	0.2437

newMI: New myocardial infarction

n	missing	distinct	Info	Sum	Mean
558	0	2	0.143	28	0.05018

newPTCA: Recent angioplasty

n	missing	distinct	Info	Sum	Mean
558	0	2	0.138	27	0.04839

newCABG: Recent bypass surgery

n	missing	distinct	Info	Sum	Mean
558	0	2	0.167	33	0.05914

death

n	missing	distinct	Info	Sum	Mean
558	0	2	0.123	24	0.04301

hxofHT: History of hypertension

n	missing	distinct	Info	Sum	Mean
558	0	2	0.625	393	0.7043

hxofDM: History of diabetes

n	missing	distinct	Info	Sum	Mean
558	0	2	0.699	206	0.3692

hxofCig: History of smoking

n	missing	distinct
558	0	3

 Value           heavy   moderate non-smoker
 Frequency         122        138        298
 Proportion      0.219      0.247      0.534

hxofMI: History of myocardial infarction

n	missing	distinct	Info	Sum	Mean
558	0	2	0.599	154	0.276

hxofPTCA: History of angioplasty

n	missing	distinct	Info	Sum	Mean
558	0	2	0.204	41	0.07348

hxofCABG: History of coronary artery bypass surgery

n	missing	distinct	Info	Sum	Mean
558	0	2	0.399	88	0.1577

any.event: Death, newMI, newPTCA, or newCABG

n	missing	distinct	Info	Sum	Mean
558	0	2	0.402	89	0.1595

ecg: Baseline electrocardiogram diagnosis

n	missing	distinct
558	0	3

 Value         normal equivocal        MI
 Frequency        311       176        71
 Proportion     0.557     0.315     0.127

# To create a separate browser window:
cat(html(w), file='desc.html')
browseURL('desc.html', browser='firefox -new-window')

Better, whether using RStudio or not:

htmlView(w, contents(d))  # or htmlView(describe(d1), describe(d2), ...)
# Use htmlViewx to use an external browser window (see above)

Or just type contents(d) with options(prType='html') in effect. This will launch a browser window if you are not in RStudio.

Nicer output from describe is obtained by separating categorical and continuous variables. The special print method used here, with options(prType='html') in effect, creates interactive sparklines so that variable values and frequencies can be looked up in spike histograms without using plotly graphics but using more basic javascript. Hover over the lowest and highest points on the histograms to see the 5 most extreme data values. Note that to initialize javascript jQuery dependencies we must include sparkline::sparkline(0) somewhere in the report before creating the first sparkline output. The qreport maketabs function is helpful here.

sparkline::sparkline(0)

maketabs(print(w, 'both'), wide=TRUE, initblank=TRUE)

Continuous
Categorical

`d` Descriptives
13 Continous Variables of 31 Variables, 558 Observations
Variable	Label	Units	n	Missing	Distinct	Info	Mean	pMedian	Gini \|Δ\|	Quantiles .05 .10 .25 .50 .75 .90 .95
bhr	Basal heart rate	bpm	558	0	69	0.999	75.29	74.5	16.57	54.0 58.0 64.0 74.0 84.0 95.3 102.0
basebp	Basal blood pressure	mmHg	558	0	94	0.998	135.3	134.5	23.35	104.0 110.0 120.0 133.0 150.0 162.3 170.1
basedp	Basal Double Product bhr*basebp	bpm*mmHg	558	0	441	1.000	10181	10016	2813	6607 7200 8400 9792 11663 13610 14770
pkhr	Peak heart rate	mmHg	558	0	105	1.000	120.6	121	25.36	81.85 90.70 106.25 122.00 135.00 147.00 155.15
sbp	Systolic blood pressure	mmHg	558	0	142	1.000	146.9	145	40.72	96 102 120 141 170 200 210
dp	Double product pkhr*sbp	bpm*mmHg	558	0	508	1.000	17634	17339	5765	10256 11341 14033 17060 20644 24536 26637
maxhr	Maximum heart rate	bpm	558	0	103	1.000	119.4	119.5	24.64	82.0 91.0 104.2 120.0 133.0 146.0 154.1
pctMphr	Percent maximum predicted heart rate achieved	%	558	0	78	0.999	78.57	78.5	16.86	53 60 69 78 88 97 104
mbp	Maximum blood pressure	mmHg	558	0	132	0.999	156	154	35.03	110.0 120.0 133.2 150.0 175.8 200.0 211.1
dpmaxdo	Double product on max dobutamine dose	bpm*mmHg	558	0	484	1.000	18550	18267	5385	11346 12865 15260 18118 21239 24893 27477
age	Age	years	558	0	62	0.999	67.34	68	13.41	46.85 51.00 60.00 69.00 75.00 82.00 85.00
baseEF	Baseline cardiac ejection fraction	%	558	0	54	0.994	55.6	57	10.71	32 40 52 57 62 65 66
dobEF	Ejection fraction on dobutamine	%	558	0	60	0.992	65.24	67	12.38	40.0 49.7 62.0 67.0 73.0 76.0 80.0

`d` Descriptives
18 Categorical Variables of 31 Variables, 558 Observations
Variable	Label	Units	n	Missing	Distinct	Info	Sum	Mean	pMedian	Gini \|Δ\|
dose	Dose of dobutamine given	mg	558	0	7	0.840		33.75	35	8.334
dobdose	Dobutamine dose at max double product	mg	558	0	8	0.941		30.24	30	10.55
gender			558	0	2
chestpain	Chest pain		558	0	2	0.640	172	0.3082
restwma	Resting wall motion abnormality on echocardiogram		558	0	2	0.745	257	0.4606
posSE	Positive stress echocardiogram		558	0	2	0.553	136	0.2437
newMI	New myocardial infarction		558	0	2	0.143	28	0.05018
newPTCA	Recent angioplasty		558	0	2	0.138	27	0.04839
newCABG	Recent bypass surgery		558	0	2	0.167	33	0.05914
death			558	0	2	0.123	24	0.04301
hxofHT	History of hypertension		558	0	2	0.625	393	0.7043
hxofDM	History of diabetes		558	0	2	0.699	206	0.3692
hxofCig	History of smoking		558	0	3
hxofMI	History of myocardial infarction		558	0	2	0.599	154	0.276
hxofPTCA	History of angioplasty		558	0	2	0.204	41	0.07348
hxofCABG	History of coronary artery bypass surgery		558	0	2	0.399	88	0.1577
any.event	Death, newMI, newPTCA, or newCABG		558	0	2	0.402	89	0.1595
ecg	Baseline electrocardiogram diagnosis		558	0	3

There is also a plot method for describe output. It produces two graphics objects: one for categorical variables and one for continuous variables. The default is to use ggplot2 to produce static graphics. The result can be fed directly into maketabs described earlier. results='asis' must appear in the chunk header.

cap <- 'Regular `plot(describe)` output'
maketabs(plot(w, bvspace=2.5), basecap=cap, cap=1)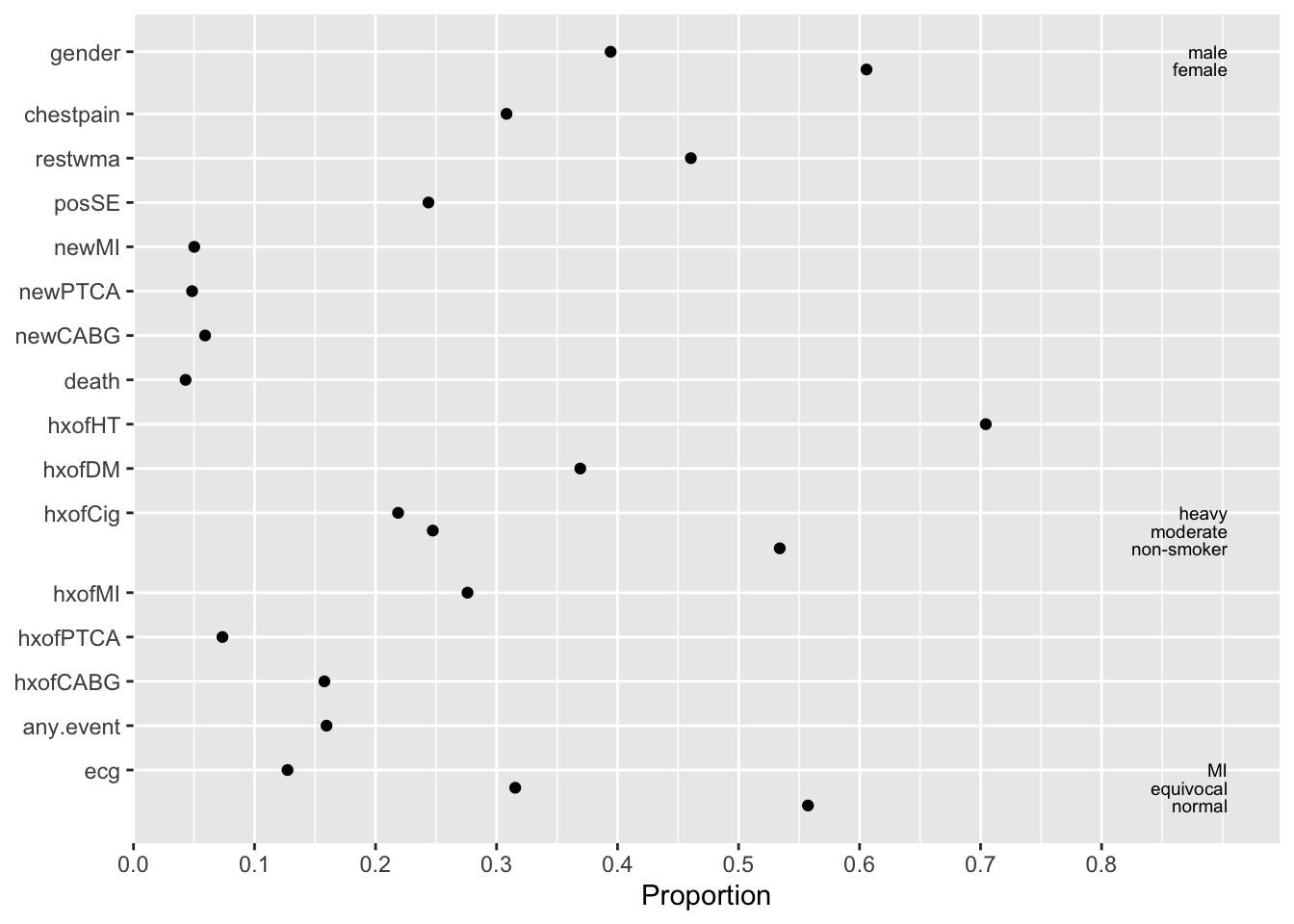

Categorical
Continuous

Figure 9.1: Regular `plot(describe)` output

By specifying grType option you can instead get plotly graphics that use hover text to show more information, especially when hovering over the leftmost dot or tick mark for a variable.

options(grType='plotly')
cap <- '`plotly` `plot(describe)` output'
maketabs(plot(w, bvspace=2.5), wide=TRUE, cap=1, basecap=cap)

Categorical
Continuous

plotly plot(describe) output

See this for other Hmisc functions for descriptive graphics and tables, especially for stratified descriptive statistics for categorical variables. The summaryM function prints a tabular summary of a mix of continuous and categorical variables. Here is an example where stratification is by history of myocardial infarction (MI).

require(data.table)
setDT(d)   # turn d into a data table
# tables() with no arguments will give a concise summary of all active data tables
w <- d
w[, hxofMI := factor(hxofMI, 0 : 1, c('No history of MI', 'History of MI'))]
vars <- setdiff(names(d), 'hxofMI')
form <- as.formula(paste(paste(vars, collapse='+'), '~ hxofMI'))
print(form)

bhr + basebp + basedp + pkhr + sbp + dp + dose + maxhr + pctMphr + mbp + dpmaxdo + dobdose + age + gender + baseEF + dobEF + chestpain + restwma + posSE + newMI + newPTCA + newCABG + death + hxofHT + hxofDM + hxofCig + hxofPTCA + hxofCABG + any.event + ecg ~ hxofMI

s <- summaryM(form, data=d, test=TRUE)
# Note: there is a problem with the width of the categorical variable
# plot.  Neither fig.size() nor options(plotlyauto=FALSE) fixed it.
maketabs(
  ` `                         ~ ` `,   # empty tab
  `Table 1`                   ~ print(s, exclude1=TRUE, npct='both', digits=3, middle.bold=TRUE),
  `Categorical Variable Plot` ~ plot(s, which='categorical', vars=1 : 4) +
                                caption('`summaryM` plots') +
                                fig.size(width=6),
  `Continuous Variable Plot`  ~ plot(s, which='continuous',  vars=1 : 4),
  wide=TRUE)

Descriptive Statistics (N=558).
	No history of MI N=404	History of MI N=154	Test Statistic
Basal heart rate bpm	65 74 85	63 72 84	F_1 556=1.41, P=0.235¹
Basal blood pressure mmHg	120 134 150	120 130 150	F_1 556=1.39, P=0.238¹
Basal Double Product bhrbasebp bpmmmHg	8514 9874 11766	8026 9548 11297	F_1 556=3.32, P=0.069¹
Peak heart rate mmHg	107 123 136	104 120 132	F_1 556=2.35, P=0.126¹
Systolic blood pressure mmHg	124 146 174	115 134 158	F_1 556=12.1, P<0.001¹
Double product pkhrsbp bpmmmHg	14520 17783 21116	13198 15539 18885	F_1 556=15, P<0.001¹
Dose of dobutamine given mg : 10	0.00 ²⁄₄₀₄	0.00 ⁰⁄₁₅₄	χ²₆=8.77, P=0.187²
15	0.05 ²¹⁄₄₀₄	0.05 ⁷⁄₁₅₄
20	0.10 ⁴⁰⁄₄₀₄	0.05 ⁷⁄₁₅₄
25	0.11 ⁴⁵⁄₄₀₄	0.07 ¹¹⁄₁₅₄
30	0.11 ⁴³⁄₄₀₄	0.14 ²¹⁄₁₅₄
35	0.11 ⁴⁵⁄₄₀₄	0.10 ¹⁶⁄₁₅₄
40	0.51 ²⁰⁸⁄₄₀₄	0.60 ⁹²⁄₁₅₄
Maximum heart rate bpm	107 122 134	102 118 130	F_1 556=4.05, P=0.045¹
Percent maximum predicted heart rate achieved %	69.0 78.0 89.0	70.0 77.0 87.5	F_1 556=0.5, P=0.479¹
Maximum blood pressure mmHg	138 154 180	130 142 162	F_1 556=13, P<0.001¹
Double product on max dobutamine dose bpm*mmHg	15654 18666 21664	14489 16785 19680	F_1 556=16.1, P<0.001¹
Dobutamine dose at max double product mg : 5	0.01 ⁴⁄₄₀₄	0.02 ³⁄₁₅₄	χ²₇=8.5, P=0.29²
10	0.01 ⁶⁄₄₀₄	0.01 ¹⁄₁₅₄
15	0.11 ⁴³⁄₄₀₄	0.08 ¹²⁄₁₅₄
20	0.14 ⁵⁸⁄₄₀₄	0.10 ¹⁵⁄₁₅₄
25	0.13 ⁵⁴⁄₄₀₄	0.11 ¹⁷⁄₁₅₄
30	0.13 ⁵¹⁄₄₀₄	0.18 ²⁷⁄₁₅₄
35	0.10 ⁴⁰⁄₄₀₄	0.14 ²²⁄₁₅₄
40	0.37 ¹⁴⁸⁄₄₀₄	0.37 ⁵⁷⁄₁₅₄
Age years	59.0 68.0 75.0	63.2 71.0 76.8	F_1 556=9.75, P=0.002¹
gender : female	0.68 ²⁷³⁄₄₀₄	0.42 ⁶⁵⁄₁₅₄	χ²₁=30, P<0.001²
Baseline cardiac ejection fraction %	55 59 63	40 54 60	F_1 556=56.4, P<0.001¹
Ejection fraction on dobutamine %	65.0 70.0 74.2	50.0 64.5 70.0	F_1 556=50.3, P<0.001¹
Chest pain	0.29 ¹¹⁹⁄₄₀₄	0.34 ⁵³⁄₁₅₄	χ²₁=1.29, P=0.257²
Resting wall motion abnormality on echocardiogram	0.57 ²³⁰⁄₄₀₄	0.18 ²⁷⁄₁₅₄	χ²₁=69.7, P<0.001²
Positive stress echocardiogram	0.21 ⁸⁶⁄₄₀₄	0.32 ⁵⁰⁄₁₅₄	χ²₁=7.56, P=0.006²
New myocardial infarction	0.03 ¹⁴⁄₄₀₄	0.09 ¹⁴⁄₁₅₄	χ²₁=7.4, P=0.007²
Recent angioplasty	0.02 ¹⁰⁄₄₀₄	0.11 ¹⁷⁄₁₅₄	χ²₁=17.8, P<0.001²
Recent bypass surgery	0.05 ²¹⁄₄₀₄	0.08 ¹²⁄₁₅₄	χ²₁=1.35, P=0.246²
death	0.04 ¹⁵⁄₄₀₄	0.06 ⁹⁄₁₅₄	χ²₁=1.23, P=0.267²
History of hypertension	0.69 ²⁸⁰⁄₄₀₄	0.73 ¹¹³⁄₁₅₄	χ²₁=0.89, P=0.346²
History of diabetes	0.36 ¹⁴⁷⁄₄₀₄	0.38 ⁵⁹⁄₁₅₄	χ²₁=0.18, P=0.674²
History of smoking : heavy	0.21 ⁸³⁄₄₀₄	0.25 ³⁹⁄₁₅₄	χ²₂=3.16, P=0.206²
moderate	0.24 ⁹⁶⁄₄₀₄	0.27 ⁴²⁄₁₅₄
non-smoker	0.56 ²²⁵⁄₄₀₄	0.47 ⁷³⁄₁₅₄
History of angioplasty	0.04 ¹⁵⁄₄₀₄	0.17 ²⁶⁄₁₅₄	χ²₁=28.4, P<0.001²
History of coronary artery bypass surgery	0.08 ³⁴⁄₄₀₄	0.35 ⁵⁴⁄₁₅₄	χ²₁=59.6, P<0.001²
Death, newMI, newPTCA, or newCABG	0.12 ⁴⁸⁄₄₀₄	0.27 ⁴¹⁄₁₅₄	χ²₁=18.1, P<0.001²
Baseline electrocardiogram diagnosis : normal	0.59 ²⁴⁰⁄₄₀₄	0.46 ⁷¹⁄₁₅₄	χ²₂=8, P=0.018²
equivocal	0.29 ¹¹⁷⁄₄₀₄	0.38 ⁵⁹⁄₁₅₄
MI	0.12 ⁴⁷⁄₄₀₄	0.16 ²⁴⁄₁₅₄
a b c represent the lower quartile a, the median b, and the upper quartile c for continuous variables. Tests used: ¹Wilcoxon test; ²Pearson test .

summaryM plots

9.1.1 Descriptive Graphics for Continuous Variables

Semi-interactive stratified spike histograms are also useful descriptive plots. These plots also contain a superset of the quantiles used in box plots, and the legend is clickable, allowing any of the statistical summaries to be turned off.

d[, histboxp(x=maxhr, group=ecg, bins=200)]

Figure 9.2: Spike histograms of heart rate stratified by ECG category

An advantage of spike histograms over regular histograms is that when no distinct values are very close together the plot shows actual data values instead of necessarily binning everything.

An exception is when the Hmisc package functions produce sparklines in tables, where uniform binning is required.

The Hmisc spikecomp function computes segment endpoints needed to construct a spike histogram. This makes it easy to draw spike histograms with ggplot2. Here histograms are annotated with quartiles.

g <- function(x) {
  z <- quantile(x, (1:3)/4, na.rm=TRUE)
  list(x=z, y1=-0.07, y2=-0.025)
}
s  <- d[, spikecomp(maxhr, tresult='segments'), by=ecg]
qu <- d[, g(maxhr), by=ecg]
ggplot(s) + geom_segment(aes(x=x, y=y1, xend=x, yend=y2, alpha=I(0.3))) +
  geom_segment(aes(x=x, y=y1, xend=x, yend=y2, col=I('red')), data=qu) +
  scale_y_continuous(breaks=NULL, labels=NULL) + ylab('') +
  facet_wrap(~ ecg) + xlab(hlab(maxhr))

1: spikecomp scales the \(y\)-axis from 0-1 for the spikes, so y1 and y2 are set to make small segments under the spikes.
2: The \(x\)-axis label was constructed from the label and units of maxhr by the Hmisc hlab function, which looked for a data table named d for this information.

Figure 9.3: Spike histograms by ECG category, with quartiles, drawn using `ggplot2`

Empirical cumulative distribution functions (ECDFs) also provide high-resolution data displays, and allow direct reading of quantiles. A large advantage of ECDFs is that they do not use binning. The Hmisc ecdfSteps function computes coordinates of the steps that make up ECDFs. This is recommended over built-in methods such as in ggplot2 because with ecdfSteps you can control how far to horizontally extend a plot at the extremes. The default is to extend the function horizontally at its 0.0 and 1.0 values to \(\frac{1}{20}^\text{th}\) of the data range on either side. For reference medians are added.

g <- function(x) {
  m <- as.double(median(x, na.rm=TRUE))
  list(x=m, y1=0, y2=0.5)
}
w <- d[, ecdfSteps(maxhr), by=ecg]
meds <- d[, g(maxhr), by=ecg]
ggplot(w, aes(x, y, color=ecg)) + geom_step() +
  geom_segment(aes(x=x, y=y1, xend=x, yend=y2, alpha=I(0.3)), data=meds) +
  xlab(hlab(maxhr)) + ylab('')

1: data.table requires consistency in the numeric storage mode. Since median can return an integer we store its result consistently in double precision floating point.

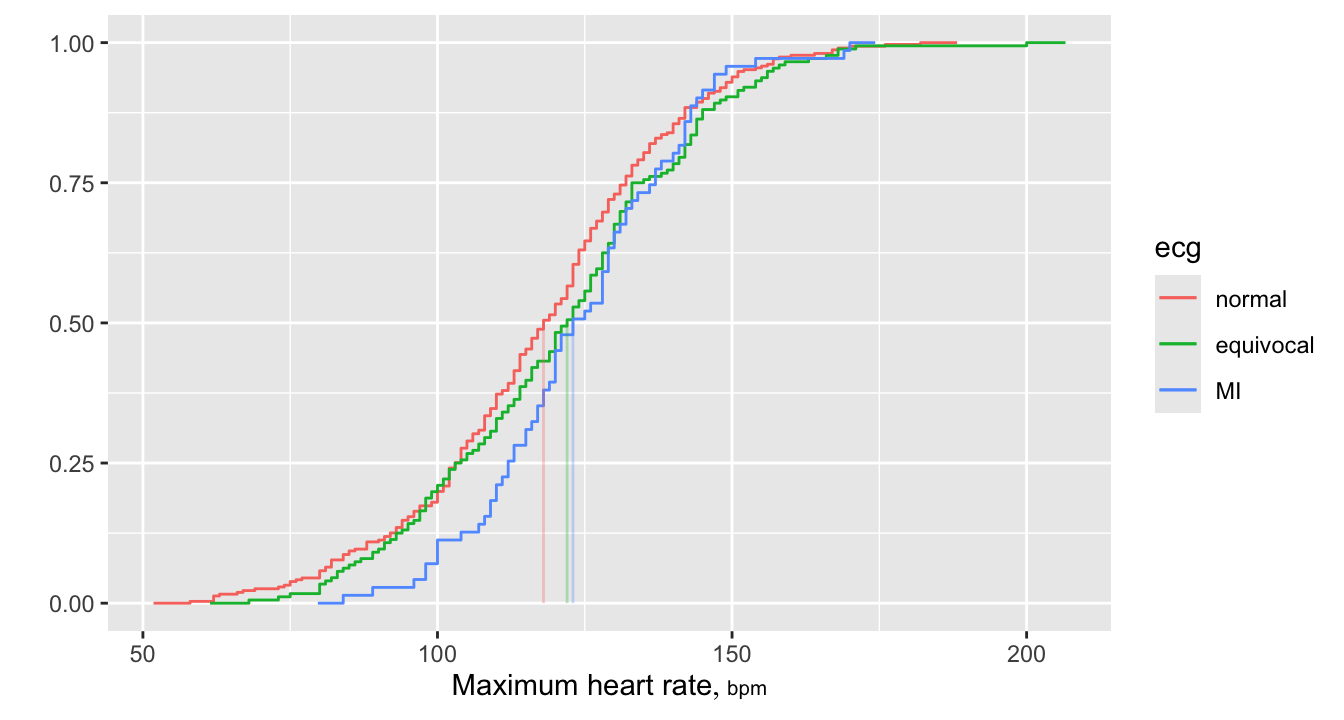
Figure 9.4: Empirical CDFs for maximum heart rate by ECG category, wth medians as vertical lines

9.2 Longitudinal Continuous Y

For a continuous response variable measured longitudinally, two of the ways to display the data are

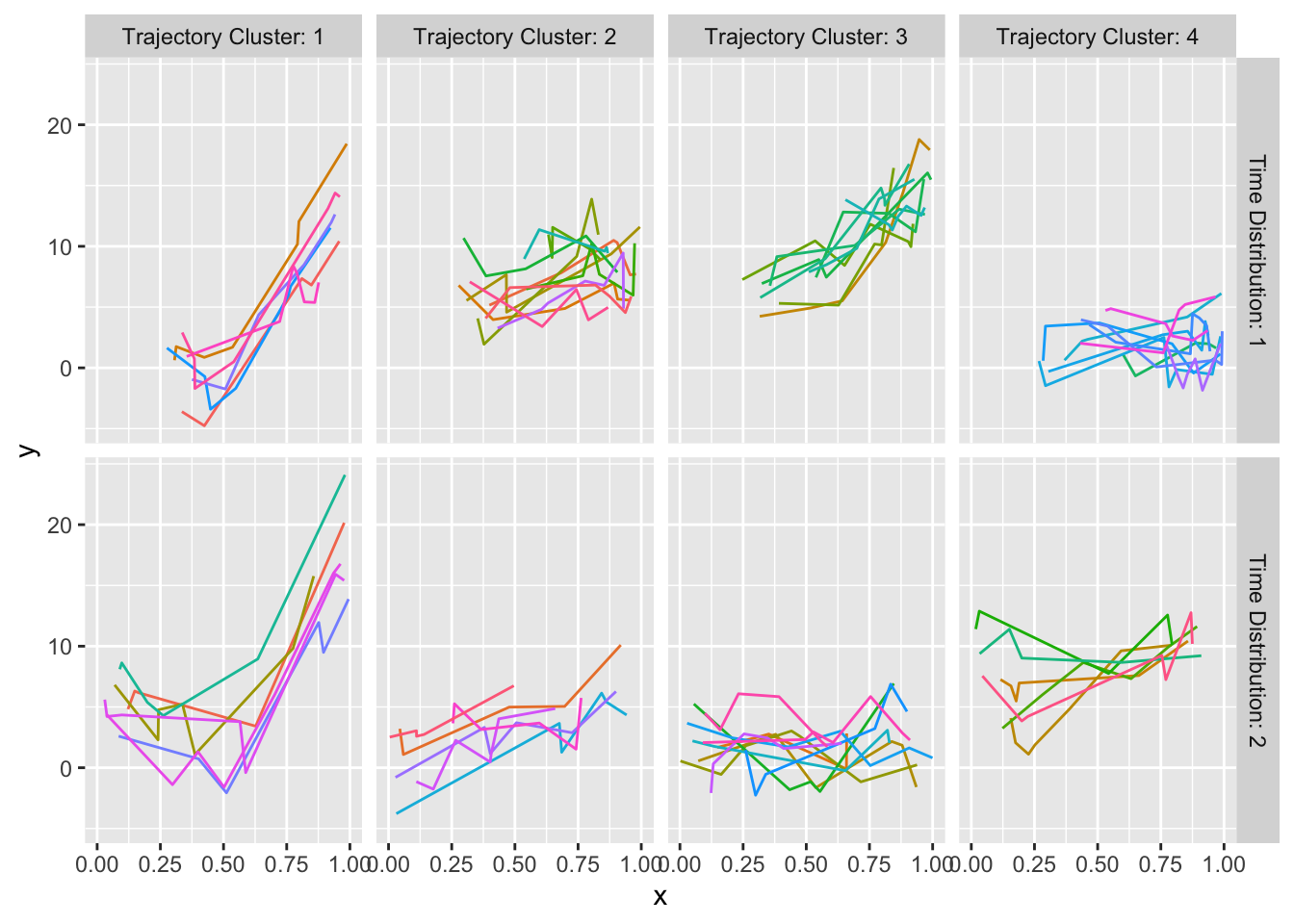
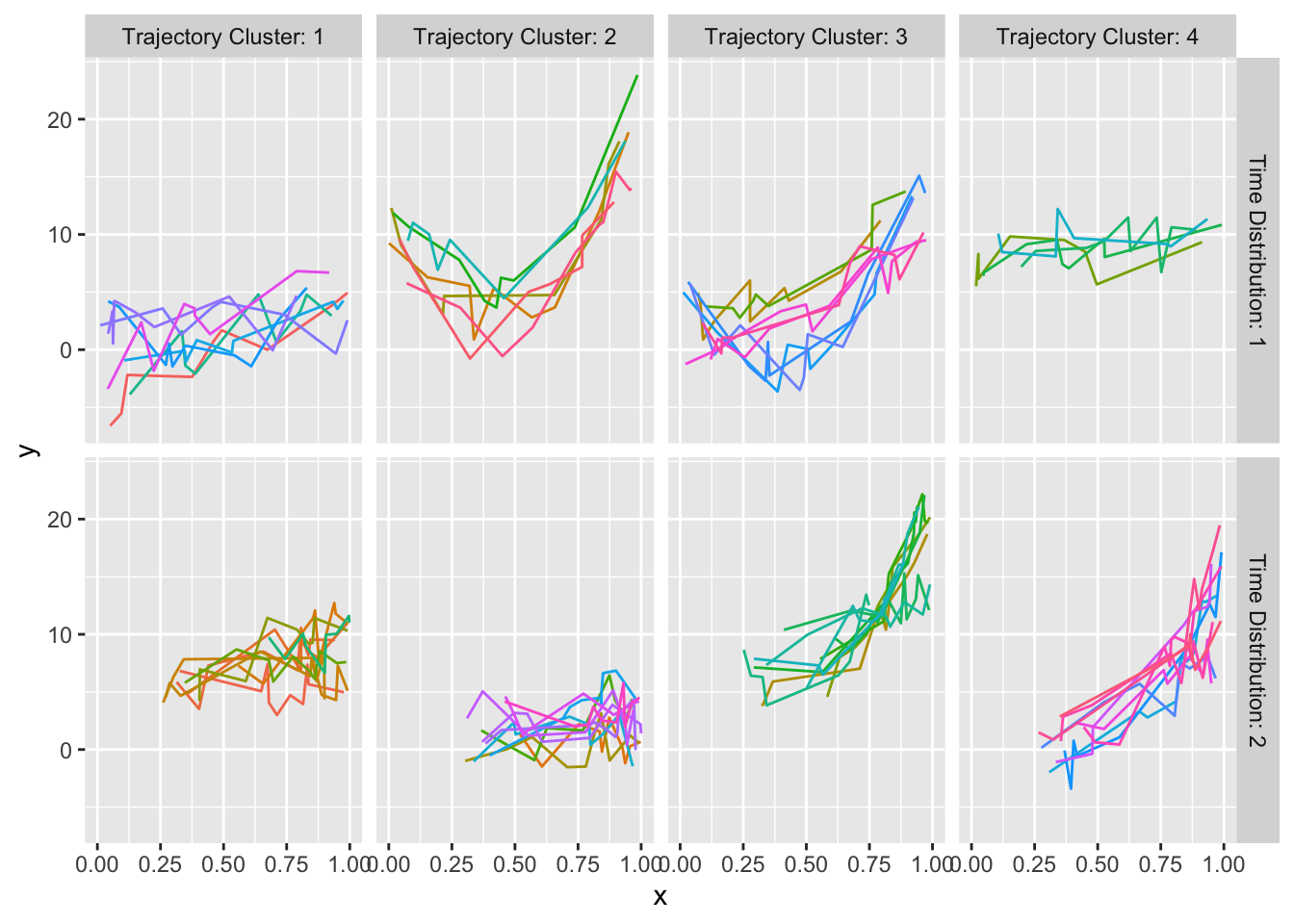
“spaghetti plots” showing all data for all individual subjects, if the number of subjects is not very large
finding clusters of individual subject curve characteristics and plotting a random sample of raw data curves within each cluster if the sample size is large

The Hmisc package curveRep function facilitates the latter approach using representative curves. It considers per-subject sample sizes and measurement time gaps as these will not only limit how we look at the data but may be informative, e.g., subjects who are failing may start to get more frequent measurements.

To demonstrate we simulate data in the following way.

Simulate 200 subjects (curves) with per-curve sample sizes ranging from 1 to 10
Make curves with odd-numbered IDs have a measurement time distribution that is random uniform [0,1] and those with even-numbered IDs have a time distribution that is half as wide but still centered at 0.5. Shift y values higher with increasing IDs
Make 1/3 of subjects have a flat trajectory, 1/3 linear and not flat, and 1/3 quadratic

Request curveRep to cluster the 200 curves on the following characteristics:

kn=3 sample size groups (curveRep actually used one more than this)
kxdist=2 time point distribution groups based here on the earliest and latest measurement times and the longest gap between any two measurements within a subject
k=4 trajectory clusters. Trajectories are determined by loess-smoothing each subject’s curve and linearly interpolating the estimates to the same evenly-spaced grid of time points, then clustering on these 10 y-estimates. This captures intercepts, slopes, and shapes.

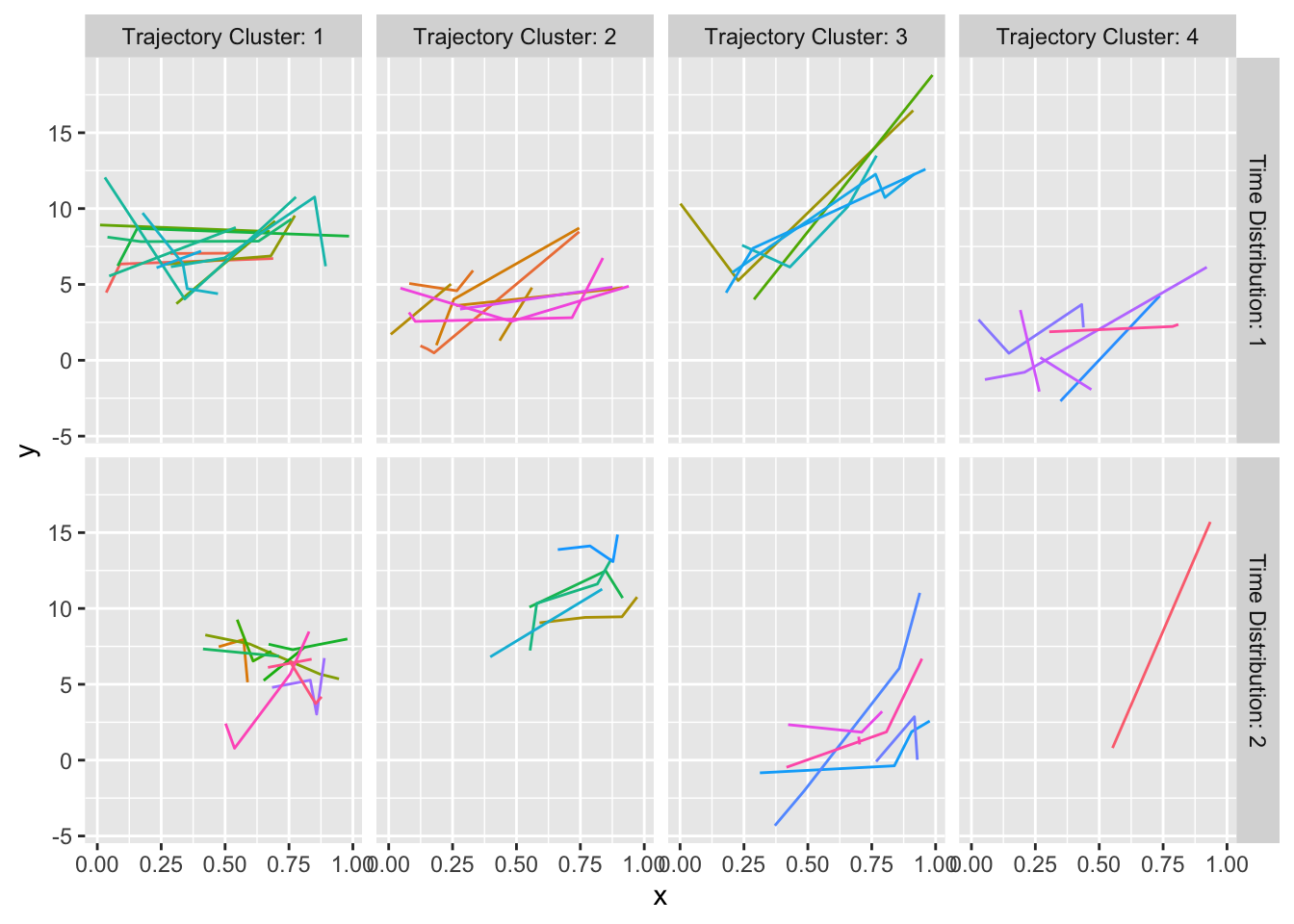
All subjects within each cluster are shown; we didn’t need to take random samples for 200 subjects. Results for the 4 per-curve sample size groups are placed in separate tabs.

set.seed(1)
N <- 200
nc <- sample(1:10, N, TRUE)
id <- rep(1:N, nc)
x  <- y <- id
# Solve for coefficients of quadratic function such that it agrees with 
# the linear function at x=0.25, 0.75 and is lower by -delta at x=0.5
delta    <- -3
cof      <- list(c(0, 0, 0), c(0, 10, 0), c(delta, 10, -2 * delta / (2 * 0.25^2)))

for(i in 1 : N) {
  x[id==i] <- if(i %% 2) runif(nc[i]) else runif(nc[i], c(.25, .75))
  shape    <- sample(1:3, 1)
  xc       <- x[id == i] - 0.5
  k        <- cof[[shape]]
  y[id == i] <- i/20 + k[1] + k[2] * xc + k[3] * xc ^ 2 +
                    runif(nc[i], -2.5, 2.5)
}
require(cluster)
w   <- curveRep(x, y, id, kn=3, kxdist=2, k=4, p=10)
gg  <- vector('list', 4)
nam <- rep('', 4)
for(i in 1 : 4) {
  z <- plot(w, i, method='data')  # method='data' available in Hmisc 4.7-1
  z <- transform(z,
                 distribution = paste('Time Distribution:', distribution),
                 cluster      = paste('Trajectory Cluster:', cluster))
  gg[[i]] <-
    if(i == 1)
      ggplot(z, aes(x, y, color=curve)) + geom_point() +
        facet_grid(distribution ~ cluster) +
        theme(legend.position='none')
  else
      ggplot(z, aes(x, y, color=curve)) + geom_line() +
        facet_grid(distribution ~ cluster) +
        theme(legend.position='none')
  nam[i] <- z$ninterval[1]
}
names(gg) <- nam
maketabs(gg, basecap='Representative curves determined by `curveRep` stratified by per-subject sample size ranges', cap=1)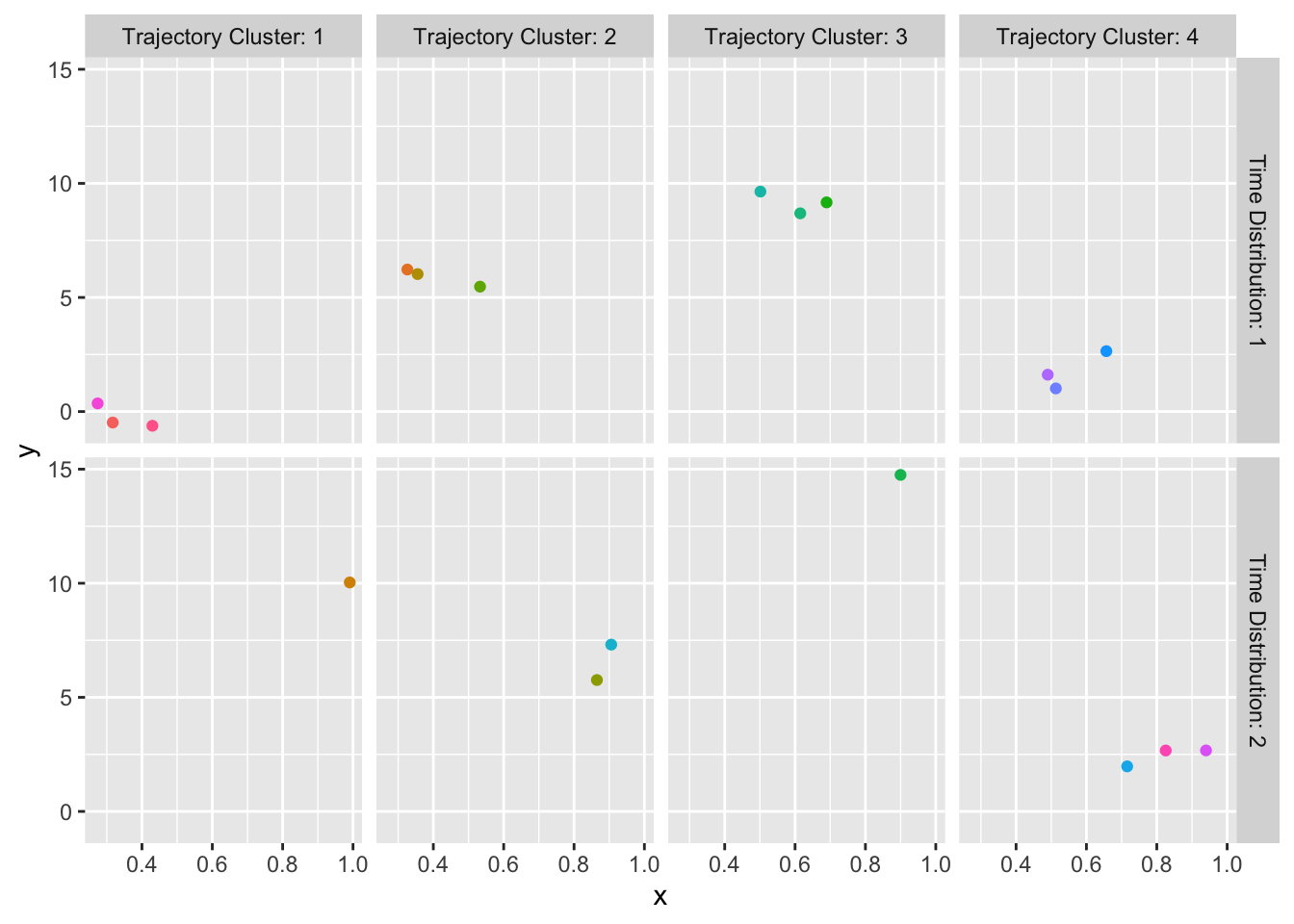

Figure 9.5: Representative curves determined by `curveRep` stratified by per-subject sample size ranges

9.3 Longitudinal Ordinal Y

Continuous longitudinal Y may be analyzed flexibly using semiparametric models while being described using representative curves as just discussed. Now suppose that Y is discrete. There are three primary ways of describing such data graphically.

Show event occurrences/trajectories for a random sample of subjects (Hmisc::multEventChart)
Show all transition proportions if time is discrete (Hmisc::propsTrans)
Show all state occupancy proportions if time is discrete (Hmisc::propsPO)

Thanks to Lucy D’Agostino McGowan for writing most of the code for multEventChart

Starting with a multiple event chart, simulate data on 5 patients, then display all the raw data.

pt1 <- data.frame(pt=1, day=0:3,
         status=.q(well, well, sick, 'very sick'))
pt2 <- data.frame(pt=2, day=c(1,2,4,6),
         status=.q(sick, 'very sick', coma, death))
pt3 <- data.frame(pt=3, day=1:5,
         status=.q(sick, 'very sick', sick, 'very sick', 'discharged'))
pt4 <- data.frame(pt=4, day=c(1:4, 10),
         status=.q(well, sick, 'very sick', well, discharged))
d <- rbind(pt1, pt2, pt3, pt4)
d <- upData(d, 
            status = factor(status, .q(discharged, well, sick,
                            'very sick', coma, death)),
            labels = c(day = 'Day'), print=FALSE)
kabl(pt1, pt2, pt3, pt4)

pt	day	status
1	0	well
1	1	well
1	2	sick
1	3	very sick

pt	day	status
2	1	sick
2	2	very sick
2	4	coma
2	6	death

pt	day	status
3	1	sick
3	2	very sick
3	3	sick
3	4	very sick
3	5	discharged

pt	day	status
4	1	well
4	2	sick
4	3	very sick
4	4	well
4	10	discharged

Figure 9.6: Multi-event chart for 4 patients

multEventChart(status ~ day + pt, data=d,
               absorb=.q(death, discharged),
               colorTitle='Status', sortbylast=TRUE) +
  theme_classic() + theme(legend.position='bottom')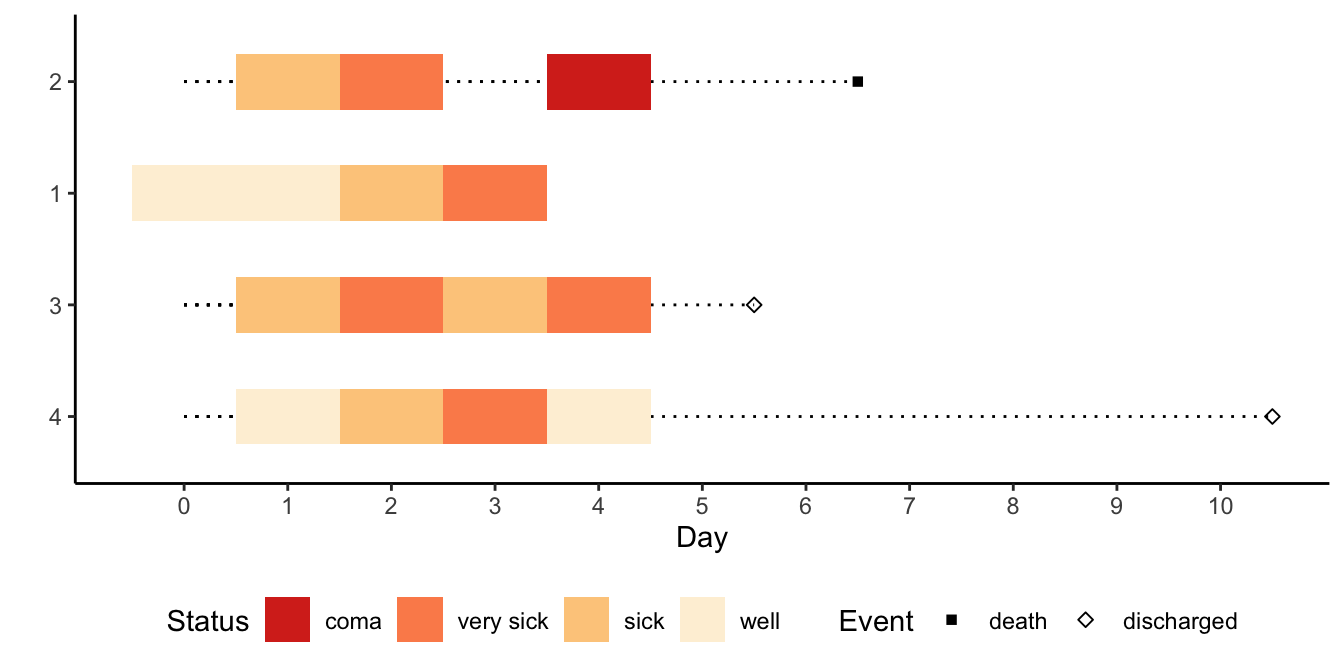

Figure 9.7: Multi-event chart for 4 patients

For an example of displaying transition proportions, whereby all the outcome information in the raw data is shown, simulate some random data. The result is a plotly graphic over which you hover the pointer to see details. The size of the bubbles is proportional to the proportion in that transition.

set.seed(1)
d <- expand.grid(id=1:30, time=1:7)
setDT(d)   # convert to data.table
d[, sex   := sample(c('female', 'male'), .N, replace=TRUE)]
d[, state := sample(LETTERS[1:4], .N, replace=TRUE)]
ggplotlyr(propsTrans(state ~ time + id, data=d))

Figure 9.8: State transition proportions

The final display doesn’t capture the within-subject correlation as done with the transition proportions, but is the most familiar display for longitudinal ordinal data as it shows proportions in the current states, which are cumulative incidence estimates for absorbing states.

Should absorbing states have occurred in the data you would need to carry these forward to the end of follow-up for propsPO to work properly, even though the real data file would terminate follow-up at an absorbing event.

ggplotlyr(propsPO(state ~ time + sex, data=d))

Figure 9.9: State occupancy proportions by time and male/female

9.4 Multiple Longitudinal Continuous Variables

When there are multiple longitudinal measurements, exploratory or descriptive analysis is more challenging. One can learn how the different longitudinal processes relate to each other by computing pairwise cross-correlations, time-stratified variable clustering, a matrix of pairwise correlation time-trends, and, in what may be called a third-order analysis, a thermometer-plot matrix of pairwise correlation coefficients where each correlation coefficient quantifies the correlation between time and the correlation coefficient between the indicated pair of variables.

Consider a longitudinal dataset of participants in a clinical trial safety study that was described here. The dataset is in the Vanderbilt Biostatistics data repository and is called safety. Fetch the data, keep only the needed variables, and show descriptive statistics.

getHdata(safety)   # Internal dataset name was All
d <- All[, .q(id, week,
              sbp, dbp, hr, axis, corr.qt, pr, qrs, rr, neutrophils,
              alat, albumin, alk.phos, asat, basophils, bilirubin, bun, 
              chloride, creatinine, eosinophils, ggt, glucose,
              hematocrit, hemoglobin, potassium, lymphocytes,
              monocytes, sodium, platelets, protein, rbc, uric.acid, wbc)]
setDT(d, key=.q(id, week))
sparkline::sparkline(0)

w <- describe(d)
maketabs(print(w, 'both'), wide=TRUE, initblank=TRUE)

Continuous
Categorical

`d` Descriptives
33 Continous Variables of 34 Variables, 16464 Observations
Variable	Label	Units	n	Missing	Distinct	Info	Mean	pMedian	Gini \|Δ\|	Quantiles .05 .10 .25 .50 .75 .90 .95
id			16464	0	2058	1.000	1030	1030	686	103.2 206.0 515.0 1029.5 1544.0 1853.0 1955.8
sbp	systolic blood pressure	mmHg	12460	4004	114	0.992	131.7	131	18.2	108 110 120 130 140 152 160
dbp	diastolic blood pressure	mmHg	12460	4004	79	0.978	78.07	78	10.51	60 68 70 80 84 90 94
hr	heart rate	bpm	12458	4006	87	0.996	76.15	76	12.12	60 63 68 76 83 90 96
axis		degree	12356	4108	326	1.000	34.43	39.5	52.36	-61 -37 7 48 70 81 88
corr.qt	corrected qt	msec	12355	4109	1832	1.000	424.2	422.2	24.27	397.3 400.6 408.0 419.6 436.4 454.7 467.1
pr		msec	12030	4434	121	0.997	158.7	156	27.08	124.0 132.0 144.0 156.0 172.0 188.0 201.5
qrs		msec	12356	4108	70	0.990	92.91	90	17.09	72 76 84 88 100 112 128
rr		msec	12356	4108	97	0.999	837.8	832.4	164.3	618.5 659.3 731.7 821.9 937.5 1034.4 1090.9
neutrophils	neutrophils absolute	10⁹/L	9079	7385	868	1.000	4.593	4.44	1.734	2.53 2.84 3.50 4.33 5.36 6.58 7.54
alat	alanine aminotransferase	IU/L	9129	7335	113	0.998	18.99	17	10.76	8 9 12 16 22 31 39
albumin		G/L	9118	7346	26	0.982	42.15	42	2.6	38 39 41 42 44 45 46
alk.phos	alkaline phosphatase	IU/L	9110	7354	185	1.000	76.3	74	24.44	46 52 61 73 87 104 118
asat	aspartate aminotransferase	IU/L	9123	7341	99	0.996	19.78	18.5	7.614	12 13 15 18 22 27 33
basophils		10⁹/L	2824	13640	596	0.999	0.03488	0.03105	0.03131	0.00000 0.00440 0.01420 0.02760 0.04900 0.07500 0.09265
bilirubin	total bilirubin	UMOL/L	9112	7352	67	0.997	10.5	10	4.72	5.13 6.00 7.00 10.00 12.00 16.00 19.00
bun	blood urea nitrogen	MMOL/L	9126	7338	174	1.000	5.776	5.65	2.051	3.200 3.600 4.500 5.500 6.783 8.200 9.000
chloride		MMOL/L	9167	7297	30	0.990	103.9	104	3.589	98 100 102 104 106 108 109
creatinine		UMOL/L	9122	7342	174	0.999	76.73	75.14	21.08	51 54 63 74 87 99 110
eosinophils		10⁹/L	2824	13640	1450	1.000	0.2289	0.207	0.1664	0.04805 0.07320 0.11800 0.19090 0.29677 0.43375 0.53868
ggt	gamma glutamyl transferase	IU/L	9114	7350	240	0.999	36.74	29.5	27.8	13 15 19 26 41 68 92
glucose	glucose - random	MMOL/L	8323	8141	349	1.000	6.055	5.678	1.797	4.200 4.500 5.000 5.600 6.384 7.900 9.688
hematocrit		%	9129	7335	265	1.000	43.83	43.85	4.356	37.5 38.9 41.3 43.9 46.3 48.6 50.1
hemoglobin		G/L	9129	7335	183	1.000	146.6	146.8	14.35	125.0 130.0 139.0 146.6 154.7 161.9 166.8
potassium		MMOL/L	9138	7326	48	0.993	4.516	4.5	0.4576	3.9 4.0 4.3 4.5 4.7 5.0 5.2
lymphocytes		10⁹/L	2824	13640	2228	1.000	1.902	1.852	0.7091	1.031 1.155 1.452 1.818 2.244 2.738 3.119
monocytes		10⁹/L	2824	13640	1492	1.000	0.4611	0.45	0.2053	0.1947 0.2451 0.3355 0.4413 0.5619 0.6911 0.7923
sodium		MMOL/L	9163	7301	33	0.985	140.8	141	3.022	136 137 139 141 143 144 145
platelets		10⁹/L	9124	7340	419	1.000	235.9	232	69.36	147 164 193 229 270 315 349
protein	total protein	G/L	9124	7340	42	0.995	70.44	70.5	4.963	63 65 67 70 73 76 78
rbc	red blood cell count	10¹²/L	9128	7336	143	0.995	4.673	4.65	0.5051	3.9 4.1 4.4 4.7 5.0 5.2 5.4
uric.acid	uric acid	UMOL/L	9142	7322	571	1.000	323.2	320.2	95.77	192.0 219.0 264.0 317.0 376.0 434.2 473.0
wbc	white blood cell count	10⁹/L	9129	7335	154	1.000	7.34	7.2	2.139	4.7 5.1 6.0 7.1 8.4 9.8 10.9

`d` Descriptives
1 Categorical Variables of 34 Variables, 16464 Observations
Variable	Label	n	Missing	Distinct	Info	Mean	pMedian	Gini \|Δ\|
week	Week	16464	0	8	0.984	7.875	8	7.782

Show the frequency distribution of the set of distinct time points per subject.

w <- d[, .(uw=paste(sort(week), collapse=' ')), by=.(id)]
w[, table(uw)]

uw
0 1 2 4 8 12 16 20 
              2058

Every subject has a record for every week. However there are many NAs for several of the variables.

plot(naclus(d))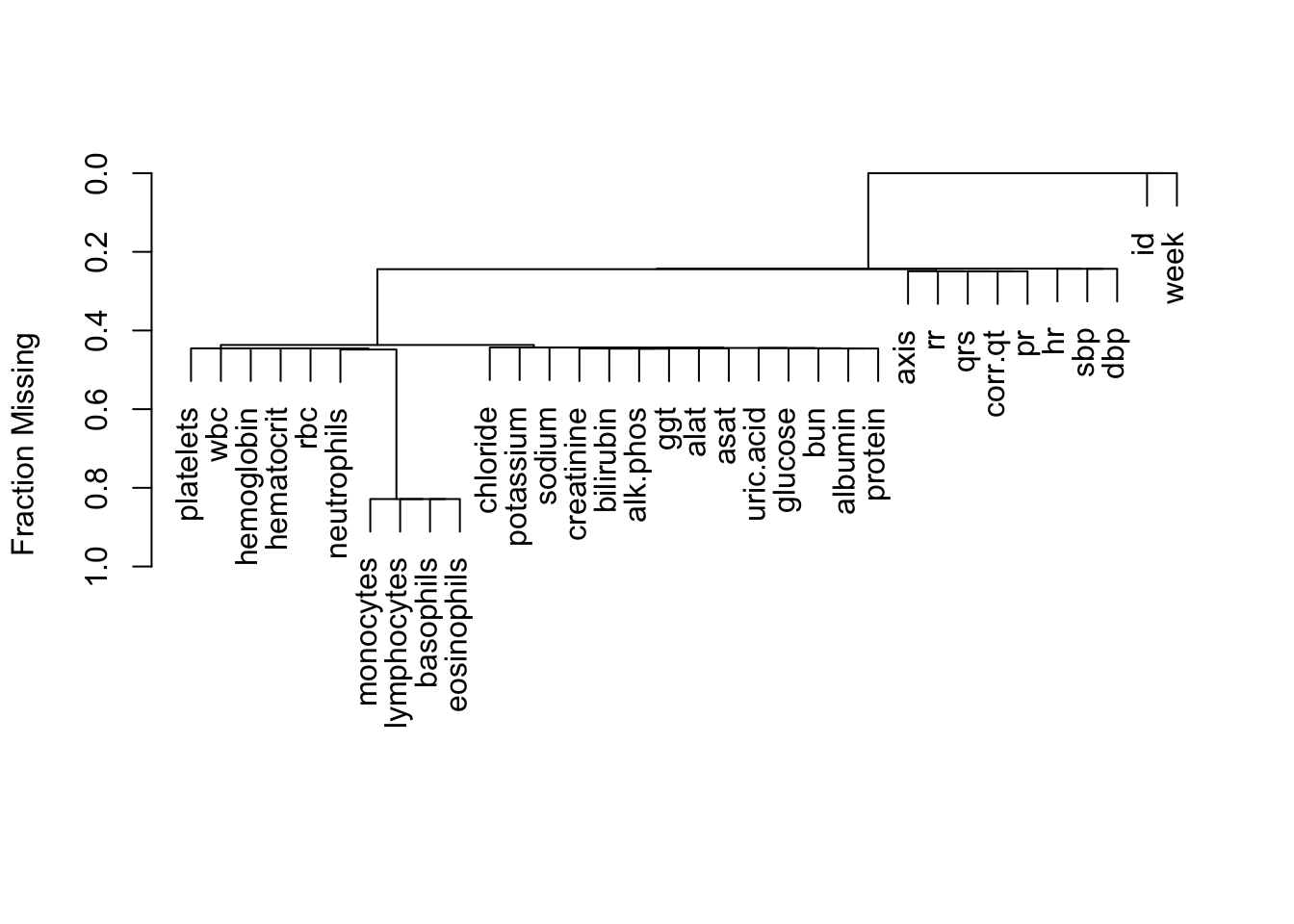

Let’s remove the variables that are missing more than 0.8 of the time.

set(d, j=.q(monocytes, lymphocytes, basophils, eosinophils), value=NULL)

9.4.1 Cross-Correlation

Compute all possible cross-correlations. The cross-correlation of two signals quantifies how closely the two signals track over time. It uses time-paired data but does not otherwise use the absolute times or the ordering of times. The dataset is a tall and thin dataset with one row per subject per time and one column per lab measurement, so it is already set up for computing cross-correlations. We just need to compute the correlations separately by subject, then average them over subjects. Spearman rank correlations are used throughout.

# Get variables to correlate
v <- setdiff(names(d), .q(week, id))
# Function to create a matrix of Spearman correlations using
# Hmisc::rcorr
r <- function(u) rcorr(as.matrix(u), type='spearman')$r
# Make a list weith raw data, one element per subject
s <- split(d[, ..v], d$id)
# Make a list of correlation matrices, one per subject
R <- lapply(s, r)
# Combine all these into an array with an extra dimension for subjects
R <- array(unlist(R), dim=c(length(v), length(v), length(R)),
           dimnames=list(v, v, NULL))
# Compute mean (separately by row and col var. combinations) 
# over subjects, ignoring NAs
R <- apply(R, 1:2, mean, na.rm=TRUE)
# Plot the matrix using Hmisc::plotCorrM
plotCorrM(R, xangle=45)[[1]]

The variables that move strongly together over time are WBC and neutrophils, RBC and hemotocrit, RBC and hemoglobin, hematocrit and hemoglobin, no surprises. Let’s see how this compares to the ordinary correlation matrix obtained by pooling all the subjects, and ignoring which measurements came from which subjects.

R <- r(d[, ..v])
plotCorrM(R, xangle=45)[[1]]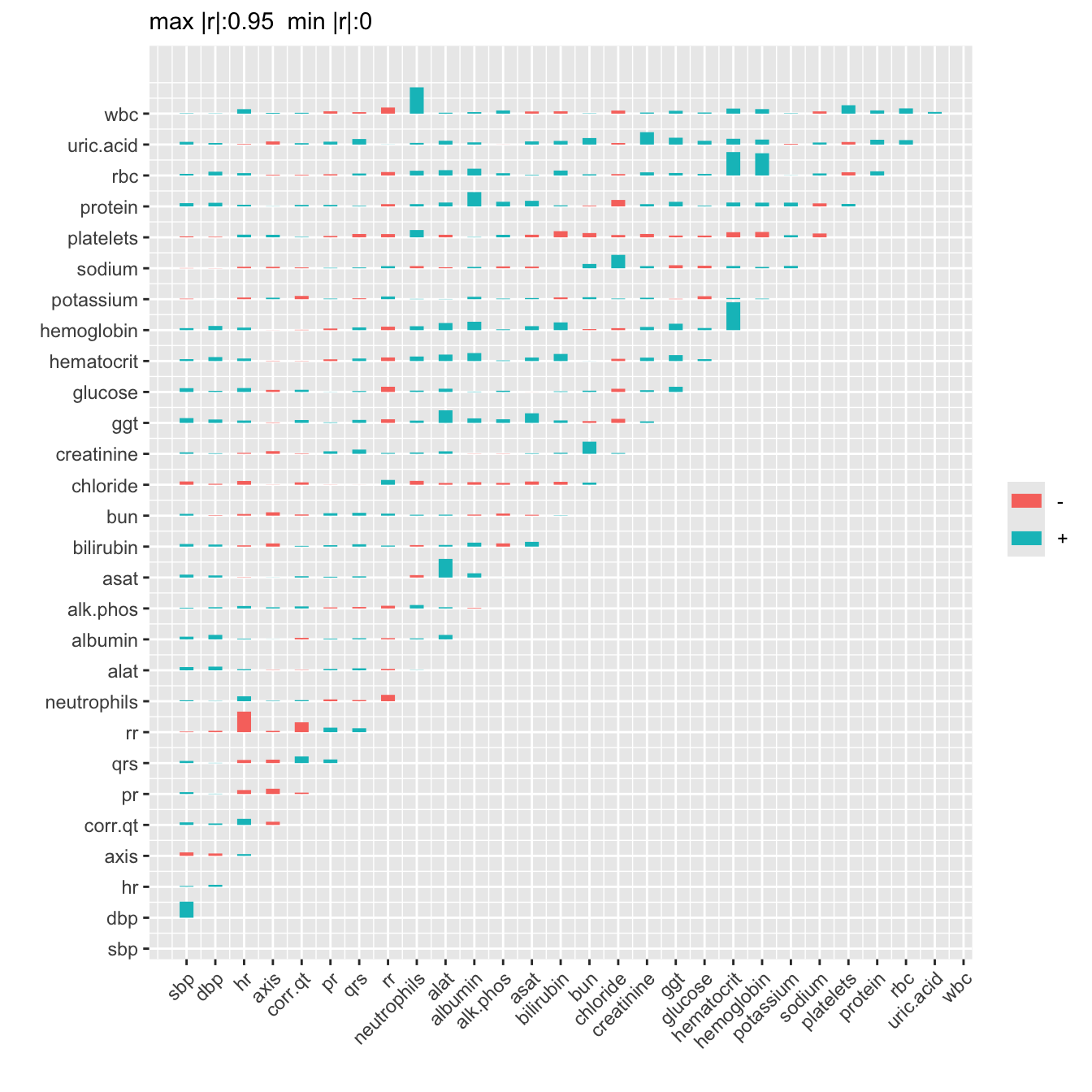

9.4.2 Time-Stratified Variable Clustering

Let’s describe how the relationships among variables appear to change over time, if they do. We do this by running variable clustering separately by follow-up time. Ignore week 1 when little data were collected.

par(mfrow=c(4,2))
g <- function(x, wk) {
  plot(varclus(as.matrix(x)))
  title(sub=paste('Week', wk), adj=0)
  invisible()
}
d[week != 1, g(.SD, week), by=.(week), .SDcols=v]

Empty data.table (0 rows and 1 cols): week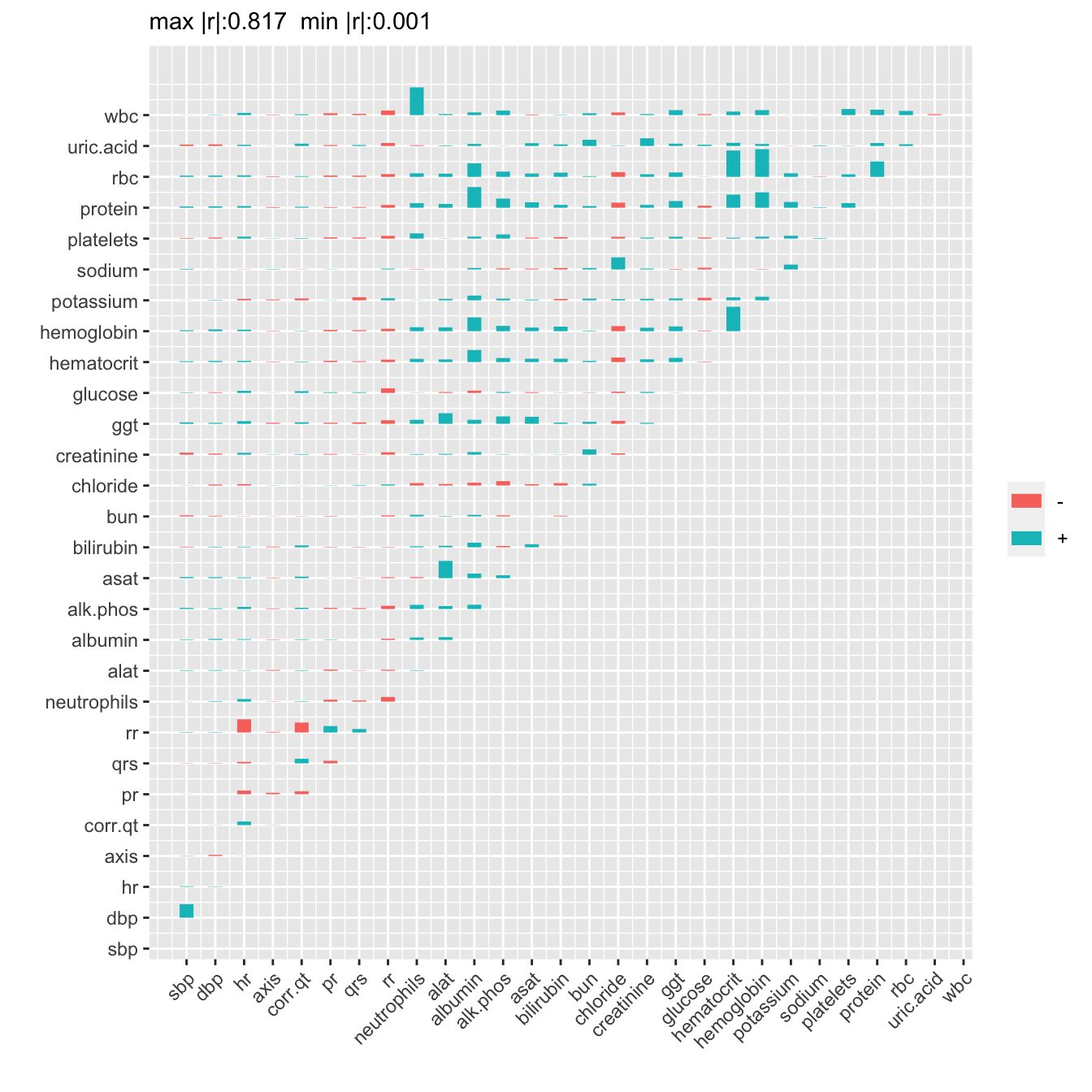

9.4.3 Time Trends in Correlations

The Hmisc package plotMultSim function takes a series of similarity matrices and plots trends in their components. The default similarity measure is the squared Spearman’s correlation coefficient. A 3-dimensional array s is used to hold similarity matrices computed for each week.

wks <- setdiff(sort(unique(d$week)), 1)
s <- array(NA, c(length(v), length(v), length(wks)),
           dimnames=list(v, v, NULL))
for(i in 1 : length(wks))
  s[, , i] <- varclus(as.matrix(d[week==wks[i], ..v]))$sim
plotMultSim(s, wks, slim=c(0,1), labelx=FALSE, xspace=5)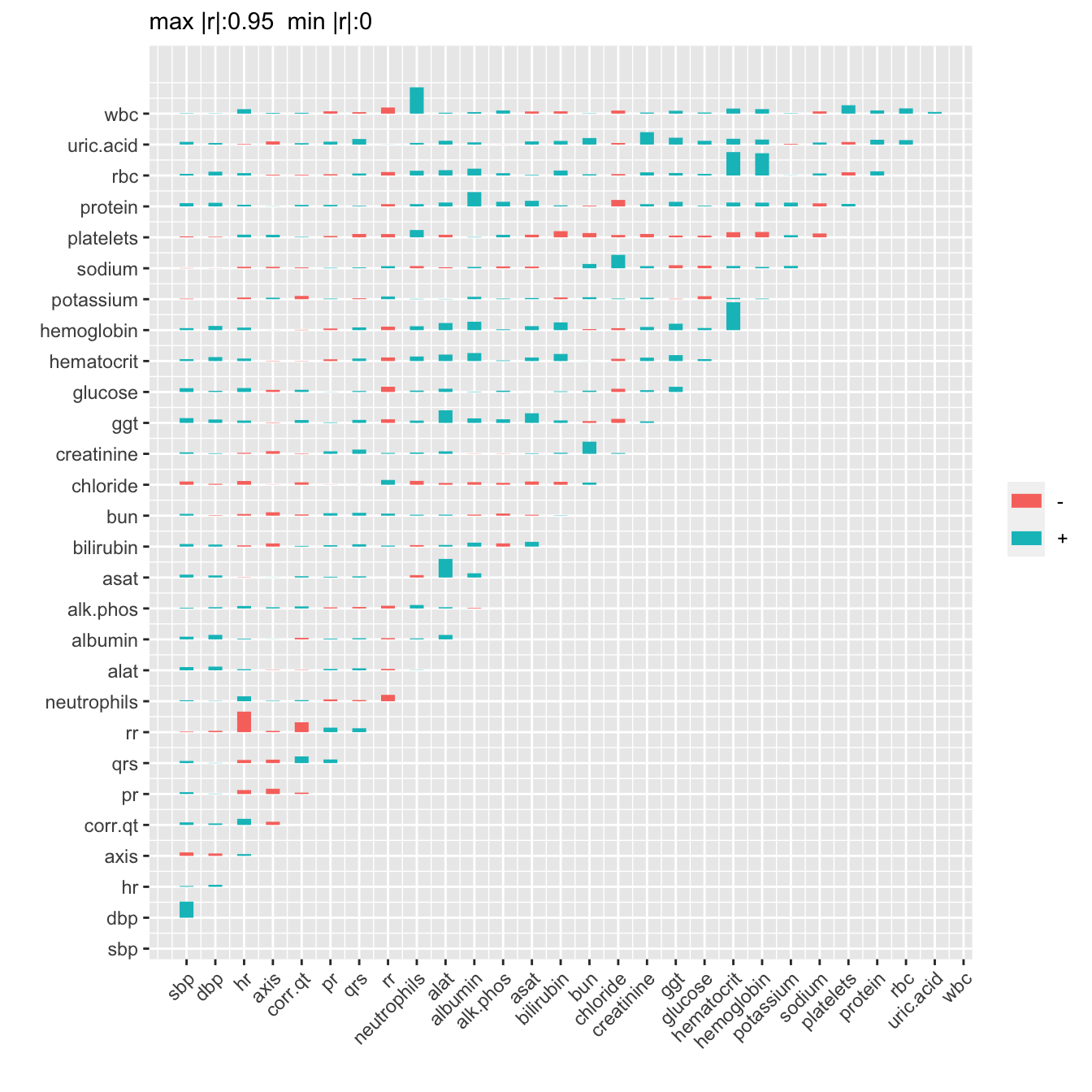

9.4.4 Correlation Time Trend Summaries

Take the similarity array just computed, and reduce it by one dimension by computing the linear correlation between time and Spearman’s \(\rho^2\).

k <- dim(s)
r <- matrix(0., nrow=k[1], ncol=k[2],
            dimnames=dimnames(s)[1:2])
for(i in 1 : k[1])
  for(j in 1 : k[2])
    if(i != j) r[i, j] <- cor(wks, s[i, j, ])
plotCorrM(r, xangle=45)[[1]]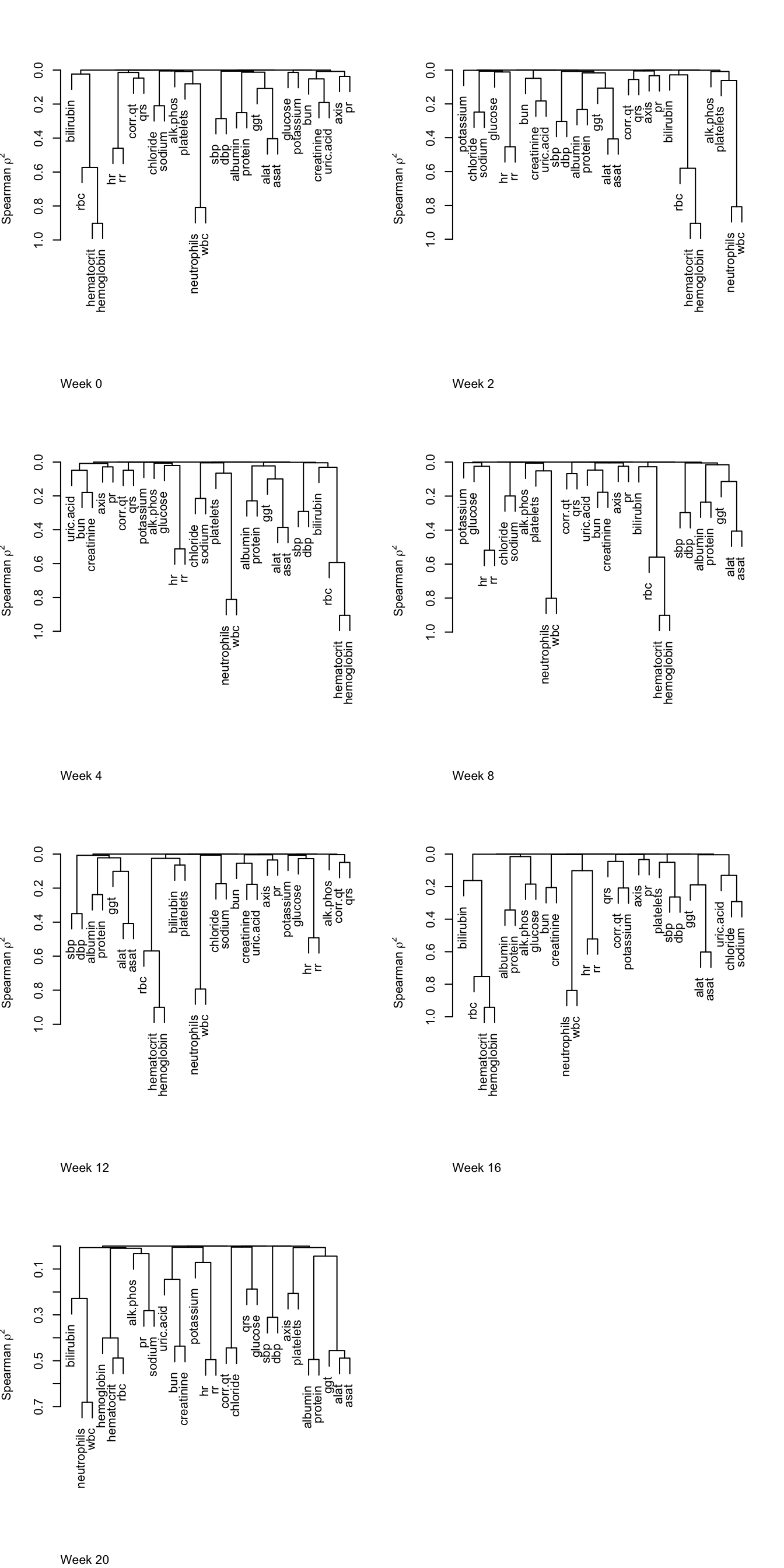

The correlation that is changing the most over time is correlation between the following two variables.

v[row(r)[abs(r) == max(abs(r))]]

[1] "wbc"       "platelets"

9.5 Adverse Event Chart

When there is a potentially large number of event types, such as adverse events (AEs) in a clinical trial, and the event timing is not considered, a dot chart is an excellent way to present the proportion of subjects suffering each type of AE. The AEs can be sorted in descending order by the difference in proportions between treatments, and plotly hover text can display more details. Half-width confidence intervals are used (see Section 15.6). An AE chart is easily produced using the aePlot function in qreport. aePlot expects the dataset to have one record per subject per AE, so the dataset itself does not define the proper denominator and this must be specified by the user (see denom below). The color coded needles in the right margin are guideposts to which denominators are being used in the analysis (details are here).

getHdata(aeTestData)  # original data source: HH package
# One record per subject per adverse event

# For this example, the denominators for the two treatments in the
# pop-up needles will be incorrect because the dataset did not have
# subject IDs.

ae <- aeTestData
# qreport requires us to define official clinical trial counts and 
# name of treatment variable
denom <- c(enrolled   = 1000,
           randomized =  400,
           a=212, b=188)

setqreportOption(tx.var='treat', denom=denom)
aePlot(event ~ treat, data=ae, minincidence=.05, size='wide')

Category	N	Used
enrolled	1000	400
randomized	400	400
a	212	212
b	188	188

Proportion of adverse events by Treatment sorted by descending risk difference. 3 events with less than 0.05 incidence in all groups are not shown (Hyperkalemia, Rash, Weight Decrease).

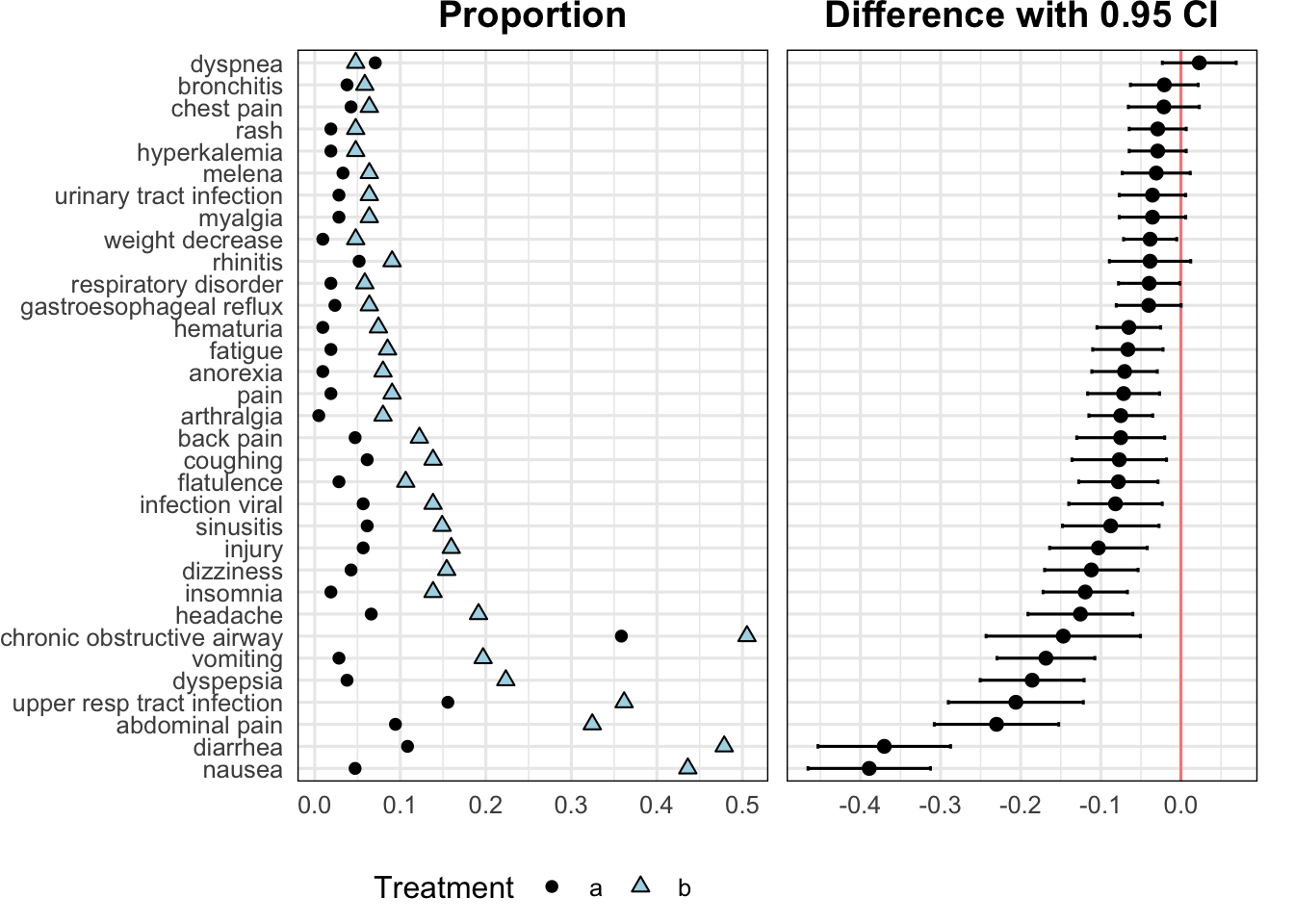
9.6 Continuous Event Times

For time-to-event data with possibly multiple types of events, an event chart is a good way to show the raw outcome data for a sample of up to perhaps 40 subjects. The Hmisc package offers the event.chart function written by Jack Lee, Kenneth Hess, and Joel Dubin. Here is an example they provided. Patients are sorted by diagnosis date.

getHdata(cdcaids)
event.chart(cdcaids,
  subset.c=.q(infedate, diagdate, dethdate, censdate),
  x.lab = 'Observation Dates',
  y.lab='Patients',
  titl='AIDS Data Calendar Event Chart',
  point.pch=c(1,2,15,0), point.cex=c(1,1,0.8,0.8),
  legend.plot=TRUE, legend.location='i', legend.cex=0.8,
  legend.point.text=.q(transfusion,'AIDS diagnosis',death,censored),
  legend.point.at = list(c(7210, 8100), c(35, 27)))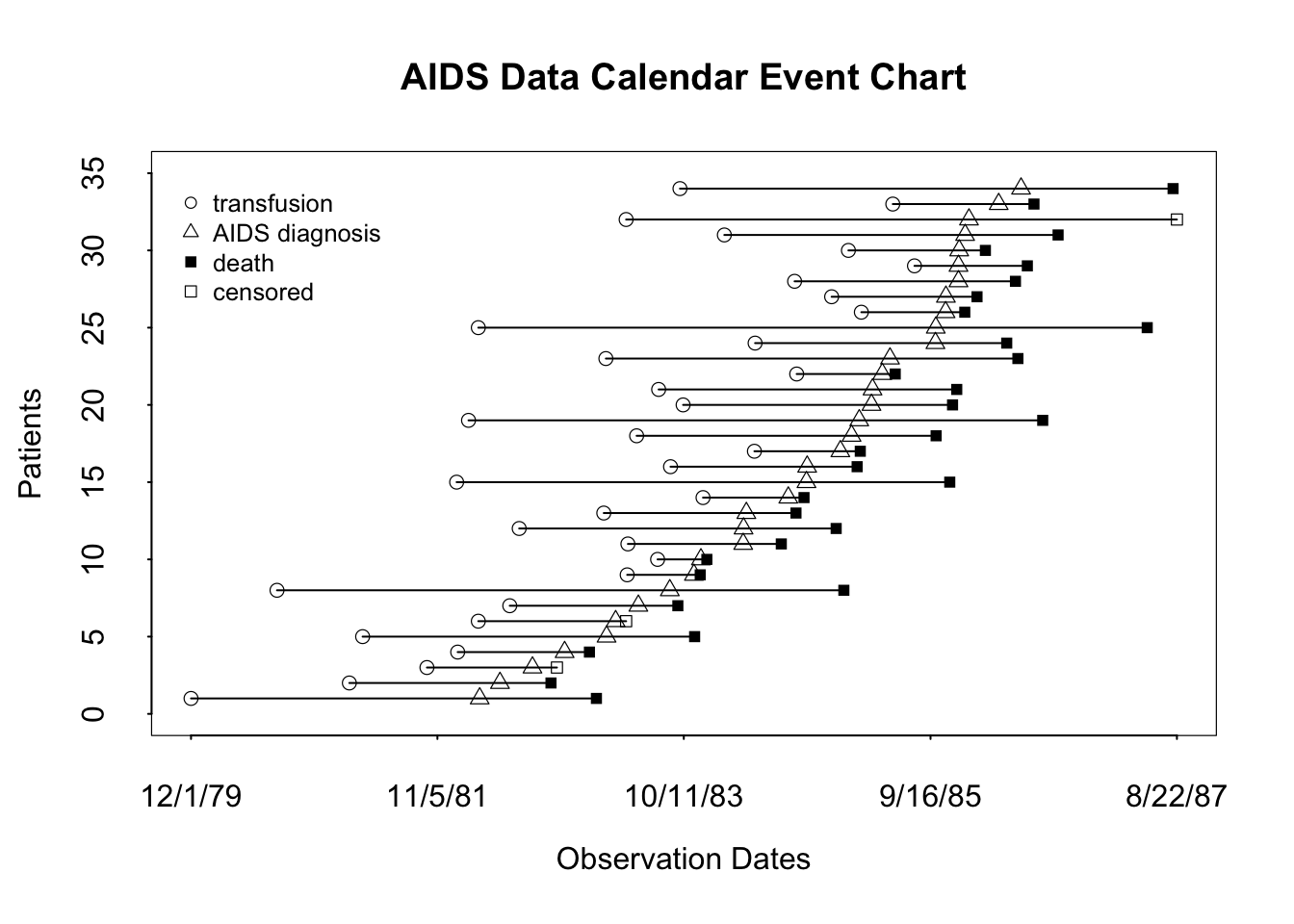

9.7 Describing Variable Interrelationships

The most basic way to examine interrelationships among variables is to graphically depict a correlation matrix. Below is an example on support using the Spearman’s \(\rho\) rank correlation coefficient. Another good descriptive analysis to help understand relationships among variables and redundancies/collinearities is variable clustering. Here one clusters on variables instead of observations, and instead of a distance matrix we have a similarly matrix. A good default similarity matrix is based on the square of \(\rho\). In order to restrict ourselves to unsupervised learning, also called data reduction, we restrict attention to non-outcome variables in both displays. The vClus function in qreport runs the dataset, after excluding some variables, through the Hmisc dataframeReduce function to eliminate variables that are missing more than 0.4 of the time and to ignore character or factor variables having more than 10 levels. Binary variables having prevalence < 0.05 are dropped, and categorical variables having < 0.05 of their non-missing values in a category will have such low-frequency categories combined into an “other” category for purposes of computing all the correlation coefficients.

Normally one would omit the fracmiss, maxlevels, minprev arguments as the default values are reasonable.

getHdata(support)
outcomes <- .q(slos,   charges, totcst,   totmcst, avtisst,
               d.time, death,   hospdead, sfdm2)
vClus(support, exclude=outcomes, corrmatrix=TRUE,
      fracmiss=0.4, maxlevels=10, minprev=0.05,
      label='fig-varclus')

Variables removed or modified
Variable	Reason
dzgroup	grouped categories
race	grouped categories
glucose	fraction missing>0.4
bun	fraction missing>0.4
urine	fraction missing>0.4
adlp	fraction missing>0.4

Correlation Matrix
Variable Clustering

Figure 9.11: Spearman rank correlation matrix. Positive correlations are blue and negative are red.

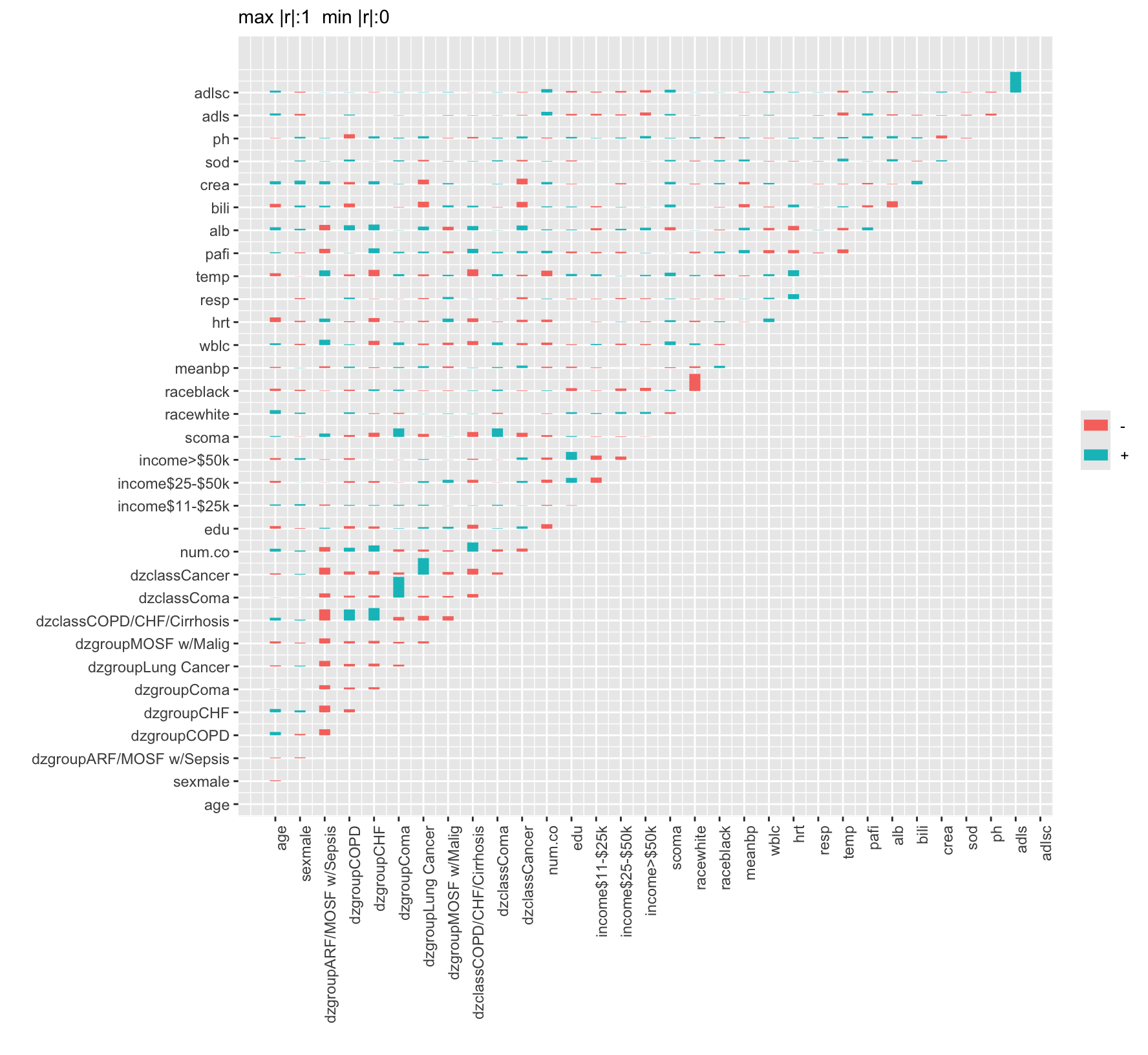
The most strongly related variables are competing indicator variables for categories from the same variable, scoma vs. dzgroup “Coma”, and dzgroup “Cancer” vs. dzclass “Cancer”. The first type of relationship generates a strong negative correlation because if you’re in one category you can’t be in the other.