Rare Degenerative Diseases & Statistics:
Methods for Analyzing Composite Patient Outcomes

Frank Harrell

Department of Biostatistics
Vanderbilt University School of Medicine
Expert Biostatistics Adviser FDA CDER

Consilium Scientific 2024-07-11
Regeneron Summer Mini-Symposium 2024-08-01

Analytical Overview

  • Many sponsors are still using minimum-power responder analysis
  • Time to event is a limited outcome
    • Time to first event ignores recurring events
    • Time to first of several events ignores severity of events
    • Time to recovery ignores unrecovery and is bothered by death

Analytical Overview, continued

  • Power gained by using a high-resolution outcome scale
    • For ordinal outcome power as # levels
  • Further gain by using multiple scales
  • Further gain by using longitudinal data
  • Need to take death + other clinical events formally into account
  • Power & making the most of N importance in rare diseases
  • A fundamental principle of statistics: maximize information extraction from raw data

RCT Outcome Overview

  • Function & symptoms important to the patient must be included
  • Results of analyzing an outcome that is masked by another are impossible to interpret
    • Example: functional status in survivors
  • Serious clinical events should be part of any outcome
  • Fundamental outcome unit: current state

RCT Outcome Overview, continued

  • On a given day, how bad is the worst thing that happened to the patient?
  • Fundamental analytical tool: longitudinal state transition models
  • Y = ordinal scale for a time period, including clinical event overrides

Analytical Options

WIN and DOOR

  • WIN ratio/odds and DOOR (desirability of outcome rankings) are longitudinal extensions of the Wilcoxon two-sample test
  • Gain power by breaking ties in time-to-event outcomes
  • Provide only within-study estimand; no clinical-scale readouts
    • Pr(randomly chosen pt on B has better outcome than pt on A)
    • How much better?
    • What is the outcome of pts on Tx B?

WIN and DOOR, continued

  • The relative ordering estimand is influenced by narrowness of study inclusion criteria
  • Similar to reporting -statistic without reporting difference in means
  • Very difficult to deal with missing component data + covariate adj.
  • Results depend on the distribution of censoring times
  • Assumes Tx affects all outcome categories equally

Ordinal Longitudinal Models (OLM)

  • Extension of Wilcoxon test and Cox model to allow covariate adjustment + repeated measures
  • Most flexible form uses a Markov process for an ordinal state transition model
  • Demonstrated to handle within-pt serial correlation almost perfectly in multiple RCTs
  • Better modeling of intra-pt correlation effective sample size
  • Elegantly handles missing components + absorbing states precluding pt scale assessment
    • Death and need for rescue therapy accounted for

OLM, continued

  • Underlying statistical parameter is a transition odds ratio for Tx
  • Huge variety of clinical readouts clinical significance
    • Pr(transitioning to state at time given in state at )
    • Pr(being at severity y or worse as a function of time, Tx)
    • Mean time in any set of states
    • Treatment difference in expected time in specified states (like time to recovery or time to loss of function)
  • Generalizes Wilcoxon test, Cox model, recurrent event analysis, and longitudinal analysis

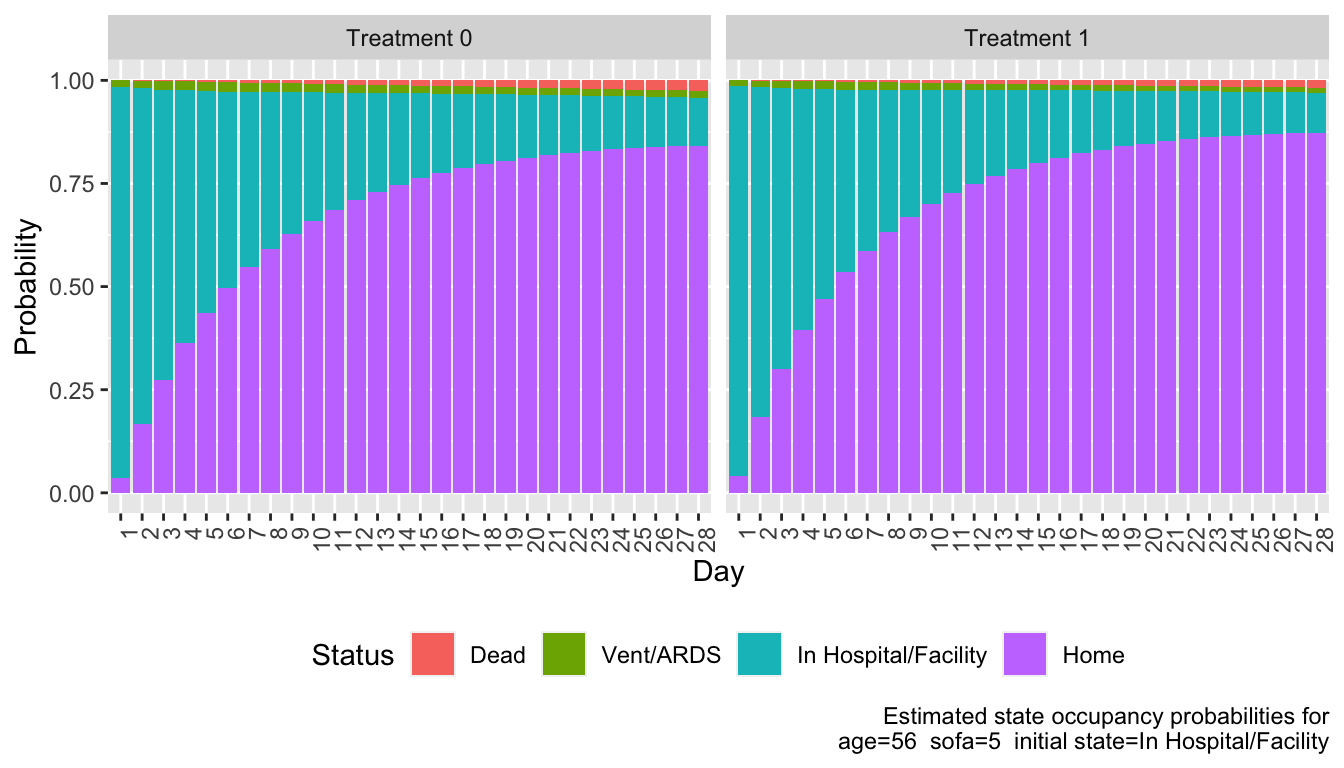
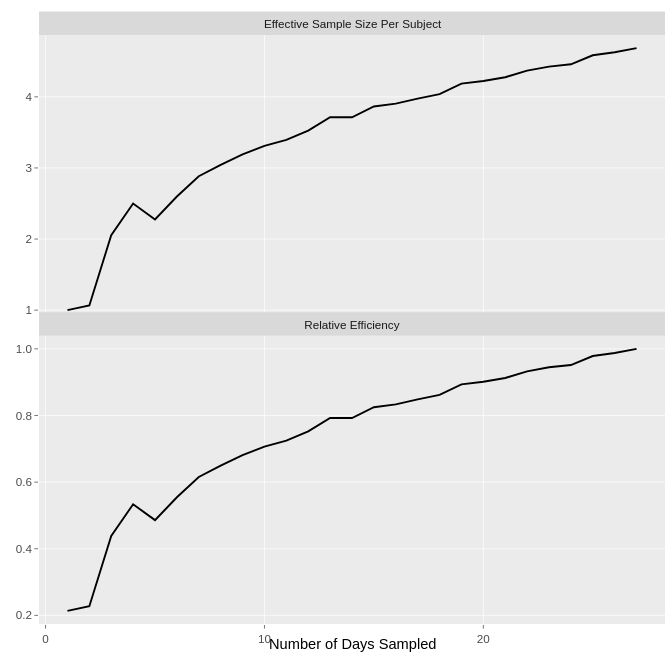
Efficiency Gain: # Visits

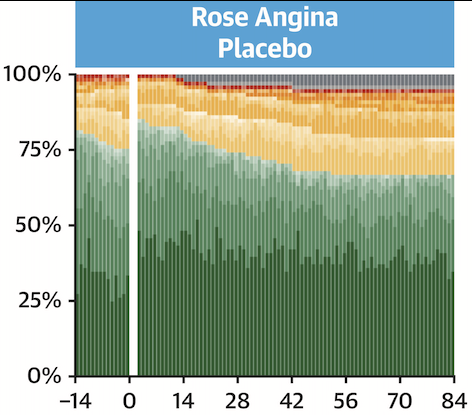
Another OLM Example: ORBITA-2

FA Simader et al (2024): Symptoms as a predictor of the placebo-controlled efficacy of PCI in stable coronary artery disease. JACC 84: 13-24.

  • Daily angina frequencies
  • Y = ordinal scale
    • Angina frequencies magnified by # units of anti-anginal meds required to control angina
    • Clinical event overrides at top of scale
    • Graphic design by Matthew Shun-Shin, Imperial College London

OLM, continued

  • OLM works for Tx that improves pt condition as well as for Tx for slowing progression
  • Detailed case study with complete R code at hbiostat.org/rmsc/markov
  • FDA CDER OB project underway to reanalyze an ALS trial using OLM

First-Order Discrete Time Markov Proportional Odds Model

  • Current state depends only on covariates, previous state
  • Let measurement times be , and the measurement for a patient at time be denoted
  • Transparent, verifiable assumptions

Markov OLM, continued

  • Simple sums of multiplied transition probabilities to uncondition on previous states state occupancy probabilities (SOPs)
  • SOPs are ITT quantities with standard causal interpretation
  • Example: death is the only outcome
  • Transition odds ratio hazard ratio
  • SOP = cumulative incidence of mortality

SOPs, continued

  • General example: SOP at 6 months
    • Probability that functional ability is worse than or patient is dead
    • Prob. that function is better than and pt is alive
  • Sum of SOPs over regularly-spaced times is mean time in state
    • Mean # days alive and well
    • Gain (difference) in mean # days alive and well due to treatment
  • Mean time in state is simple even with time treatment interaction present

Unified Approach

  • Standard longitudinal continuous
  • Longitudinal continuous or ordinal interrupted by clinical events
  • Easily handles multiple absorbing states
  • Serial correlation: condition on previous outcome
  • Random intercepts (compound symmetry correlation): condition on average of all previous outcomes

Examples of Longitudinal Ordinal Outcomes

  • 0=alive 1=dead
    • censored at 3w: 000
    • death at 2w: 01
  • 0=at home 1=hospitalized 2=MI 3=dead
    • hospitalized at 3w, rehosp at 7w, MI at 8w & stays in hosp, f/u ends at 10w: 0010001211

Examples, continued

  • 0-6 QOL excellent--poor, 7=MI 8=stroke 9=dead
    • QOL varies, not assessed in 3w but pt event free, stroke at 8w, death 9w: 12[0-6]334589
    • MI status unknown at 7w: 12[0-6]334[5,7]89
  • Can make first 200 levels be a continuous response variable and the remaining values represent clinical event overrides

Extension of OLM: Partial Proportional Odds Markov Model

  • Allows effect of Tx to vary over outcome categories
  • Example: Tx may affect mortality differently than how it affects function/Sx
  • Bayesian prior can specify limits on the amount of borrowing of Tx effects across outcomes
  • Example Bayesian posterior prob.: probability that Tx affects death by effect on function
  • See fharrell.com/post/yborrow

Composite Outcome Scales

  • Choice of scales is very important
  • Gold standard is pt utility for current status
  • OLM approximates the gold standard
  • Several ways to combine multiple scales

Analyzing Multiple Scales That Can't Be Combined Into an Ordinal Scale

  • Multiple functional / symptom / QOL scales at a given time
  • Not recommended: combining separate -values
  • Time-trade-off to arrive at overall utility, but difficult
  • Ordinal regression to relate all scales to an ultimate outcome or pt global scale
  • Projects all scales into a single global scale for OLM

How to Analyze Multiple Scales, continued

  • Take one outcome scale as an anchor, calibrate all scales to it
    • Compute optimum weighted average of scales
    • Treat as ordinal
    • Add clinical event overrides
  • Put all scales on the same Likert scale
    • Ask pt which scale is most important to them
    • Use that scale for that patient, as ordinal

A Completely Different Approach (Bayesian)

  • Bayesian multivariate model using all scales
    • Copula or correlated random effects to model scale dependencies
  • For outcome measures compute the Bayesian posterior probability that the treatment benefits pts on at least of these
  • Probability treatment has any effect on some of the outcomes and a major effect on one particular outcome

More Information

Usage: marp --html talk.md

See https://www.hashbangcode.com/article/seven-tips-getting-most-out-marp