Code
f <- orm(gh ~ rcs(age,5) + sex + re + rcs(bmi, 3), data=w, x=TRUE, y=TRUE)
ordParallel(f)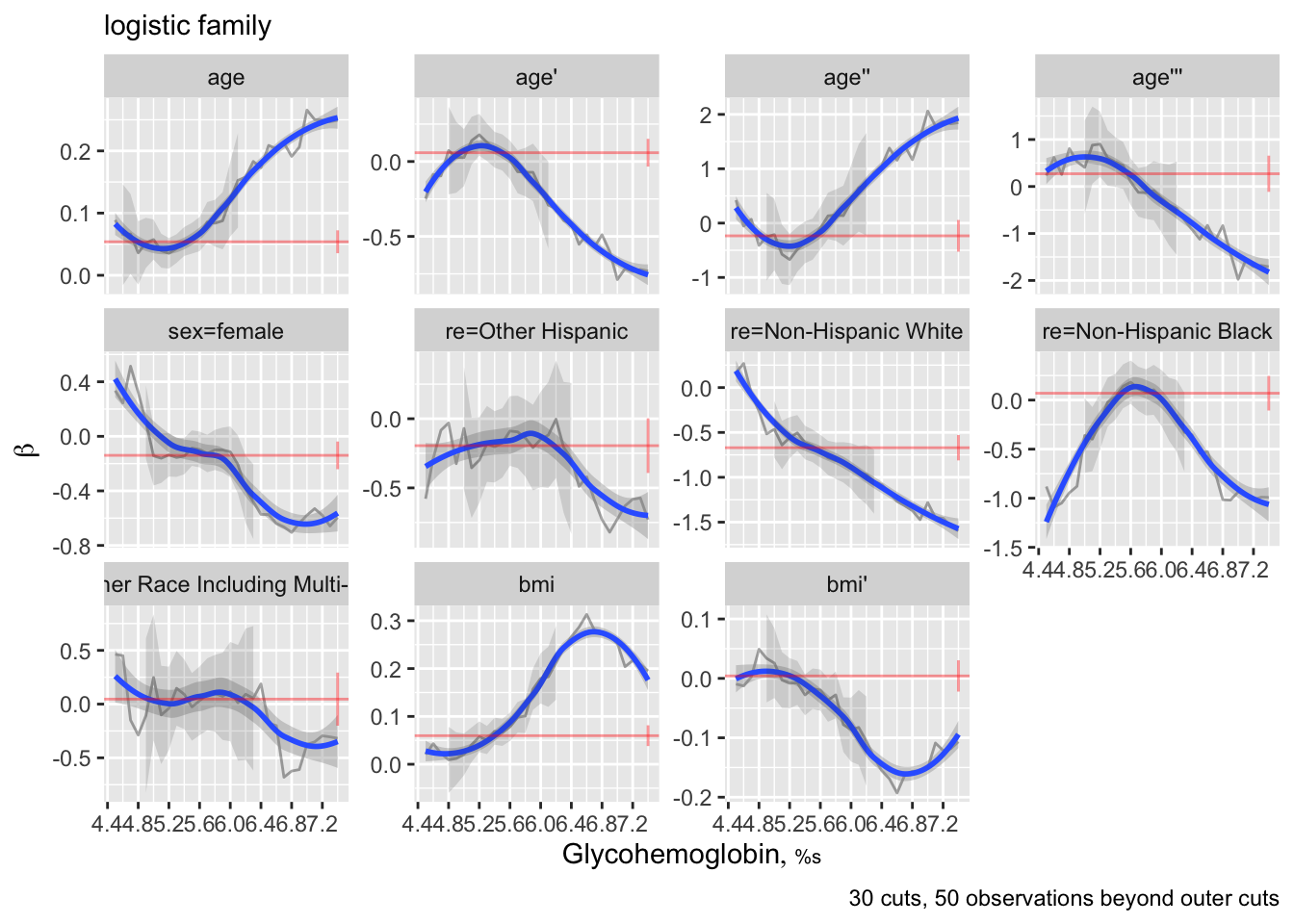
This chapter concerns univariate continuous \(Y\). There are many multivariable models for predicting such response variables.
Semiparametric models that treat \(Y\) as ordinal but not interval-scaled have many advantages including robustness and freedom of distributional assumptions for \(Y\) conditional on any given set of predictors. Advantages are demonstrated in a case study of a cumulative probability ordinal model. Some of the results are compared to quantile regression and OLS. Many of the methods used in the case study also apply to ordinary linear models.
bmi, just for the spike histogramsw Descriptives |
|||||||||||
| 15 Continous Variables of 18 Variables, 4629 Observations | |||||||||||
| Variable | Label | Units | n | Missing | Distinct | Info | Mean | pMedian | Gini |Δ| | Quantiles .05 .10 .25 .50 .75 .90 .95 |
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| seqn | Respondent sequence number | 4629 | 0 | 4629 | 1.000 | 56902 | 56902 | 3501 | 52136 52633 54284 56930 59495 61079 61641 | ||
| age | Age | years | 4629 | 0 | 703 | 1.000 | 48.57 | 48.29 | 19.85 | 23.33 26.08 33.92 46.83 61.83 74.83 80.00 | |
| wt | Weight | kg | 4629 | 0 | 890 | 1.000 | 80.49 | 78.9 | 22.34 | 52.44 57.18 66.10 77.70 91.40 106.52 118.00 | |
| ht | Standing Height | cm | 4629 | 0 | 512 | 1.000 | 167.5 | 167.4 | 11.71 | 151.1 154.4 160.1 167.2 175.0 181.0 184.8 | |
| bmi | Body Mass Index | kg/m2 | 4629 | 0 | 1994 | 1.000 | 28.59 | 28.02 | 6.965 | 20.02 21.35 24.12 27.60 31.88 36.75 40.68 | |
| leg | Upper Leg Length | cm | 4474 | 155 | 216 | 1.000 | 38.39 | 38.4 | 4.301 | 32.0 33.5 36.0 38.4 41.0 43.3 44.6 | |
| arml | Upper Arm Length | cm | 4502 | 127 | 156 | 1.000 | 37.01 | 37 | 3.116 | 32.6 33.5 35.0 37.0 39.0 40.6 41.7 | |
| armc | Arm Circumference | cm | 4499 | 130 | 290 | 1.000 | 32.87 | 32.65 | 5.475 | 25.4 26.9 29.5 32.5 35.8 39.1 41.4 | |
| waist | Waist Circumference | cm | 4465 | 164 | 716 | 1.000 | 97.62 | 96.9 | 17.18 | 74.8 78.6 86.9 96.3 107.0 117.8 125.0 | |
| tri | Triceps Skinfold | mm | 4295 | 334 | 342 | 1.000 | 18.94 | 18.7 | 9.463 | 7.2 8.8 12.0 18.0 25.2 31.0 33.8 | |
| sub | Subscapular Skinfold | mm | 3974 | 655 | 329 | 1.000 | 20.8 | 20.6 | 9.124 | 8.60 10.30 14.40 20.30 26.58 32.00 35.00 | |
| gh | Glycohemoglobin | % | 4629 | 0 | 63 | 0.994 | 5.533 | 5.5 | 0.5411 | 4.8 5.0 5.2 5.5 5.8 6.0 6.3 | |
| albumin | Albumin | g/dL | 4576 | 53 | 26 | 0.990 | 4.261 | 4.25 | 0.3528 | 3.7 3.9 4.1 4.3 4.5 4.7 4.8 | |
| bun | Blood urea nitrogen | mg/dL | 4576 | 53 | 50 | 0.995 | 13.03 | 12.5 | 5.309 | 7 8 10 12 15 19 22 | |
| SCr | Creatinine | mg/dL | 4576 | 53 | 167 | 1.000 | 0.8887 | 0.855 | 0.2697 | 0.58 0.62 0.72 0.84 0.99 1.14 1.25 | |
w Descriptives |
|||||
| 3 Categorical Variables of 18 Variables, 4629 Observations | |||||
| Variable | Label | n | Missing | Distinct | |
|---|---|---|---|---|---|
| sex | 4629 | 0 | 2 | ||
| re | Race/Ethnicity | 4629 | 0 | 5 | |
| income | Family Income | 4389 | 240 | 14 | |
The most popular multivariable model for analyzing a univariate continuous \(Y\) is the the linear model \[ E(Y | X) = X \beta, \] where \(\beta\) is estimated using ordinary least squares, that is, by solving for \(\hat{\beta}\) to minimize \(\sum (Y_{i} - X \hat{\beta})^{2}\).
1 The latter assumption may be dispensed with if we use a robust Huber-White or bootstrap covariance matrix estimate. Normality may sometimes be dispensed with by using bootstrap confidence intervals, but this would not fix inefficiency problems with OLS when residuals are non-normal.
gh would make a Gaussian residuals model fit gh to these strata and check for normality and constant \(\sigma^2\)f <- ols(gh ~ rcs(age,5) + sex + re + rcs(bmi, 3), data=w)
setDT(w) # make w a data.table
w[, pgh := fitted(f)]
w[, pgh6 := cut2(pgh, g=6)]
u <- w[, ecdfSteps(gh, extend=FALSE), by=pgh6] # ecdfSteps is in Hmisc
v <- rbind(data.table(trans='paste(Phi^-1, (F[n](x)))', u[, z := qnorm(1 - y) ]),
data.table(trans='logit(F[n](x))', u[, z := qlogis(1 - y) ]),
data.table(trans='-log(-log(F[n](x)))', u[, z := -log(-log(1 - y))]),
data.table(trans='log(-log(1-F[n](x)))', u[, z := log(-log(y)) ]))
v <- v[! is.infinite(z)]
ggplot(v, aes(x, z, color=pgh6)) + geom_step() +
facet_wrap(~ trans, label='label_parsed', scales='free_y') +
xlab(expression(HbA[`1c`])) + theme(legend.position='bottom')
# Get slopes of pgh for some cutoffs of Y
# Use glm complementary log-log link on Prob(Y < cutoff) to
# get log-log link on Prob(Y >= cutoff)
r <- NULL
for(link in c('logit','probit','cloglog'))
for(k in c(5, 5.5, 6)) {
co <- coef(glm(gh < k ~ pgh, data=w, family=binomial(link)))
r <- rbind(r, data.frame(link=link, cutoff=k,
slope=round(co[2],2)))
}
print(r, row.names=FALSE) link cutoff slope
logit 5.0 -3.39
logit 5.5 -4.33
logit 6.0 -5.62
probit 5.0 -1.69
probit 5.5 -2.61
probit 6.0 -3.07
cloglog 5.0 -3.18
cloglog 5.5 -2.97
cloglog 6.0 -2.51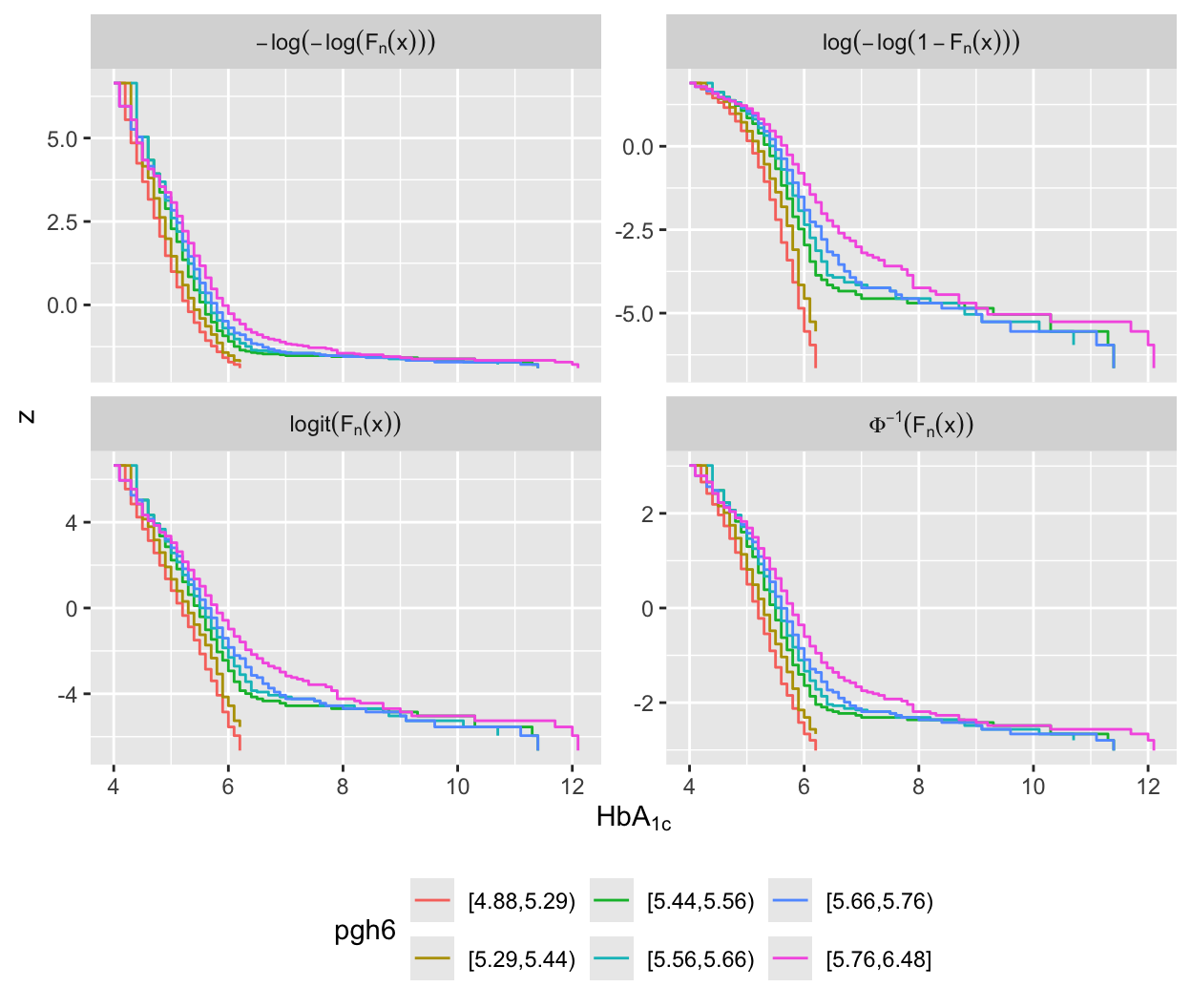
gh22 They are not parallel either.
The rms ordParallel function makes it easy to vary coefficients over a continuum of cutoffs, and it has a algorithm for choosing cutpoints given a specify maximum number of cutoffs. As this allows different predictors to have different amounts of non-parallelism, this may be preferred to the 6-tiles approach.
When there are multiple terms, it is difficult to interpret this plot. There is an option to combine all the terms for each predictor into a single partial linear predictor. Then y-varying effects are assessed with respect to this predictor summary measure. By default these partial linear predictors are scaled by their inter-quartile-range over observations so that weak predictors will not have exaggerated/irrelevant y-cutoff-dependencies.
The above two plots were for the logit link. Re-run using the log-log link.
Effects appear to be more constant.
ordParallel has an onlydata option to make it produce a data frame instead of a graphic. The data frame is a stacked version of all the one-number “terms” summaries. The number of observations in the stacked data frame will be the number of cuts multiplied by the number of observations. A variable obs is included in the data frame so that one can see which original observation numbers correspond to each row of the stacked data. obs can be used as the cluster argument to rms::robcov to get robust cluster sandwich variance-covariance matrix estimates. These can be used to get wald tests for interactions between cutoffs and covariate, i.e., tests of parallelism. The following example shows how to do this for the two link functions.
testpar <- function(form, link) {
f <- orm(form, data=w, family=link, x=TRUE, y=TRUE)
do <- ordParallel(f, onlydata=TRUE, maxcuts=30)
g <- orm(Yge_cut ~ (age + sex + bmi + re) * Ycut, data=do, x=TRUE, y=TRUE)
h <- robcov(g, do$obs)
print(anova(h))
invisible()
}
form <- gh ~ rcs(age,5) + sex + re + rcs(bmi, 3)
testpar(form, 'logistic') # Chunk test for global parallelism 151.17
testpar(form, 'loglog') # Chunk test 140.8Another approach to goodness of fit is internal calibration plots. For a series of gh cutoffs plot the estimated actual probability of exceeding the cutoff as a function of the predicted probability of exceeding it.
Calibration-in-the-large:
y Mean Predicted P(Y > y) Observed P(Y > y)
5.5 0.41770 0.42623
6.0 0.09299 0.09419
6.5 0.02870 0.02636
7.0 0.01650 0.01339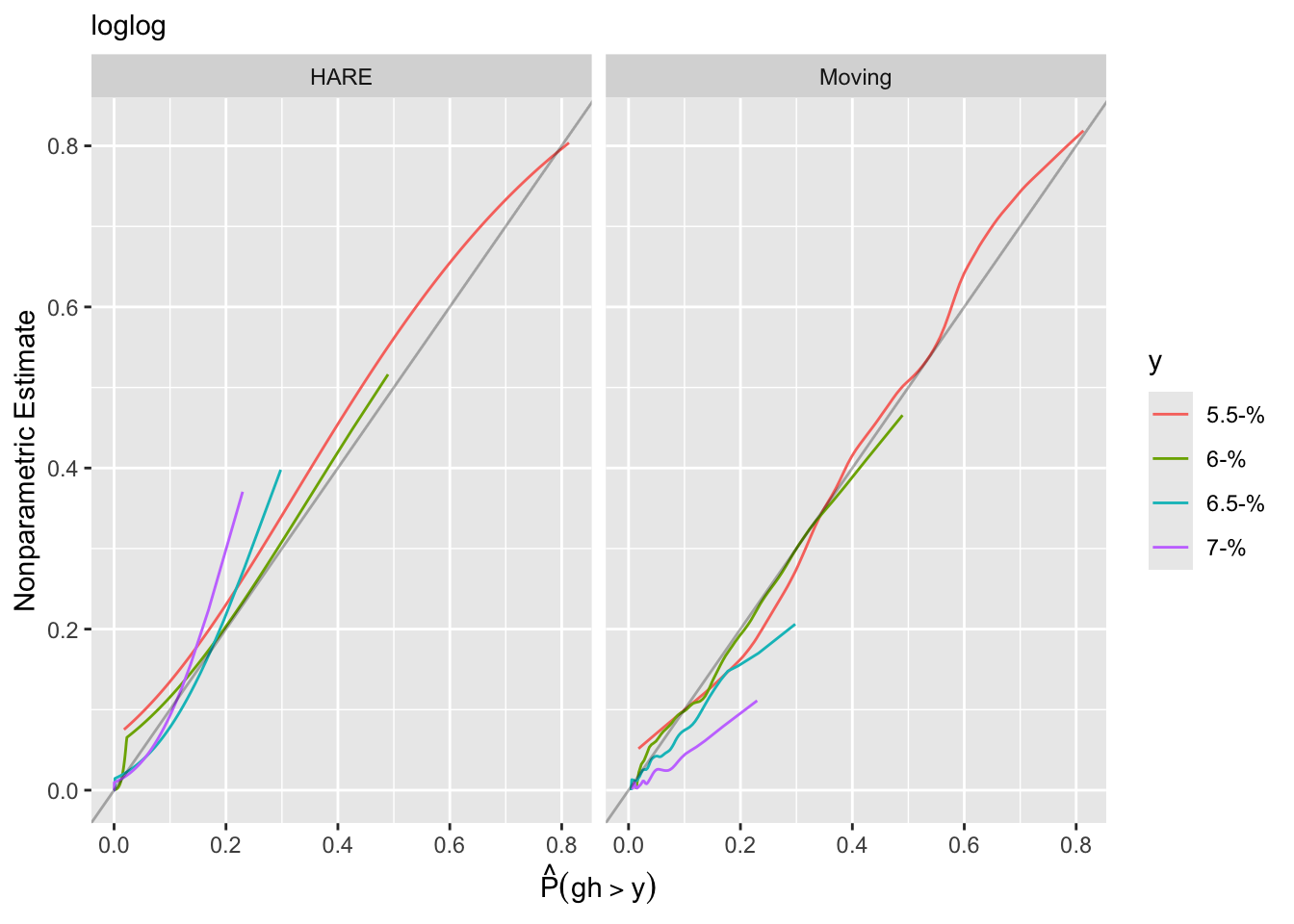
Calibration-in-the-large:
y Mean Predicted P(Y > y) Observed P(Y > y)
5.5 0.43578 0.42623
6.0 0.09590 0.09419
6.5 0.02646 0.02636
7.0 0.01338 0.01339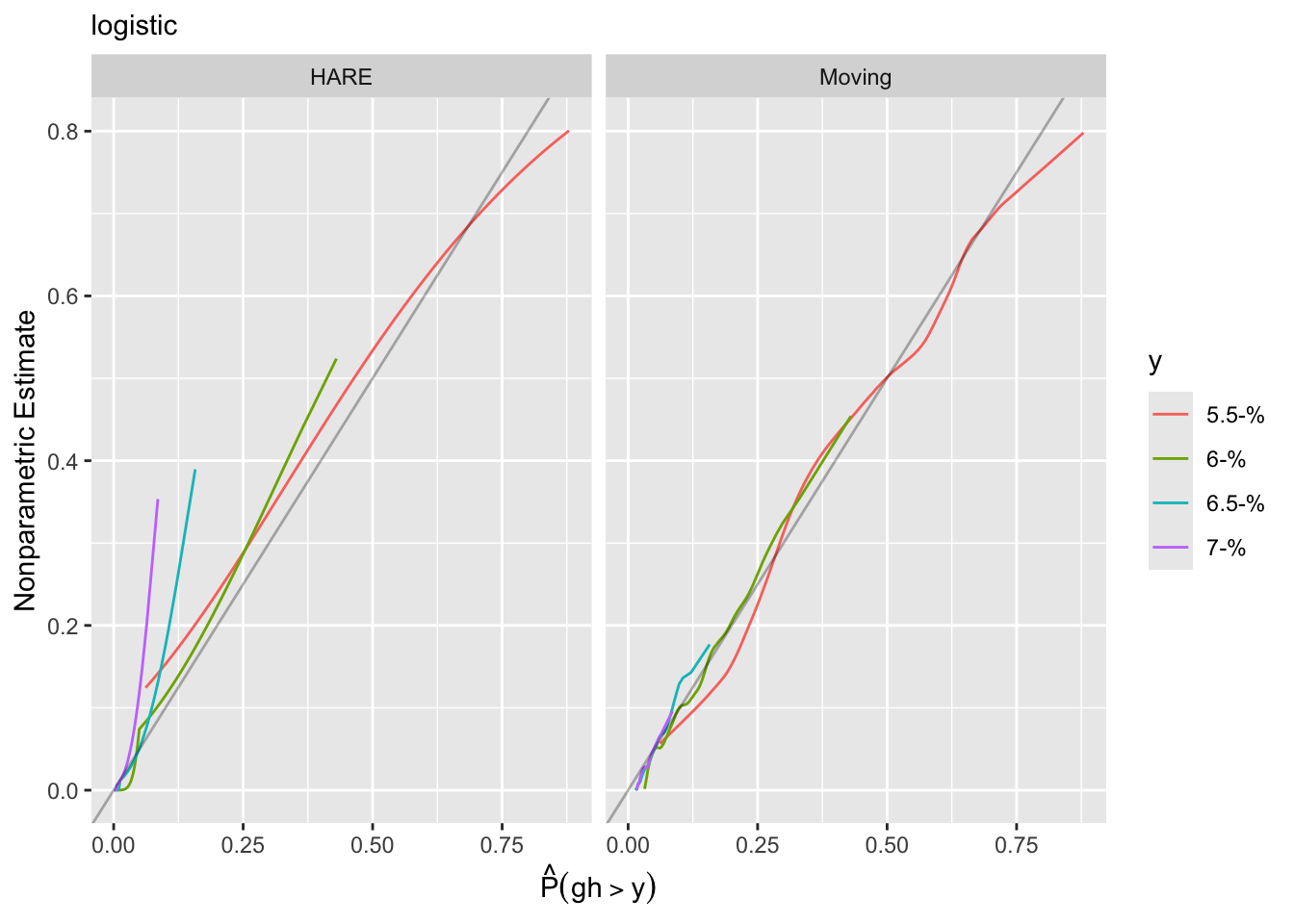
Using the adaptive linear spline HARE estimates, the logit link fits less well.
A different calibration plan is made by plotting both predicted and observed exceedance probabilities against a covariate.
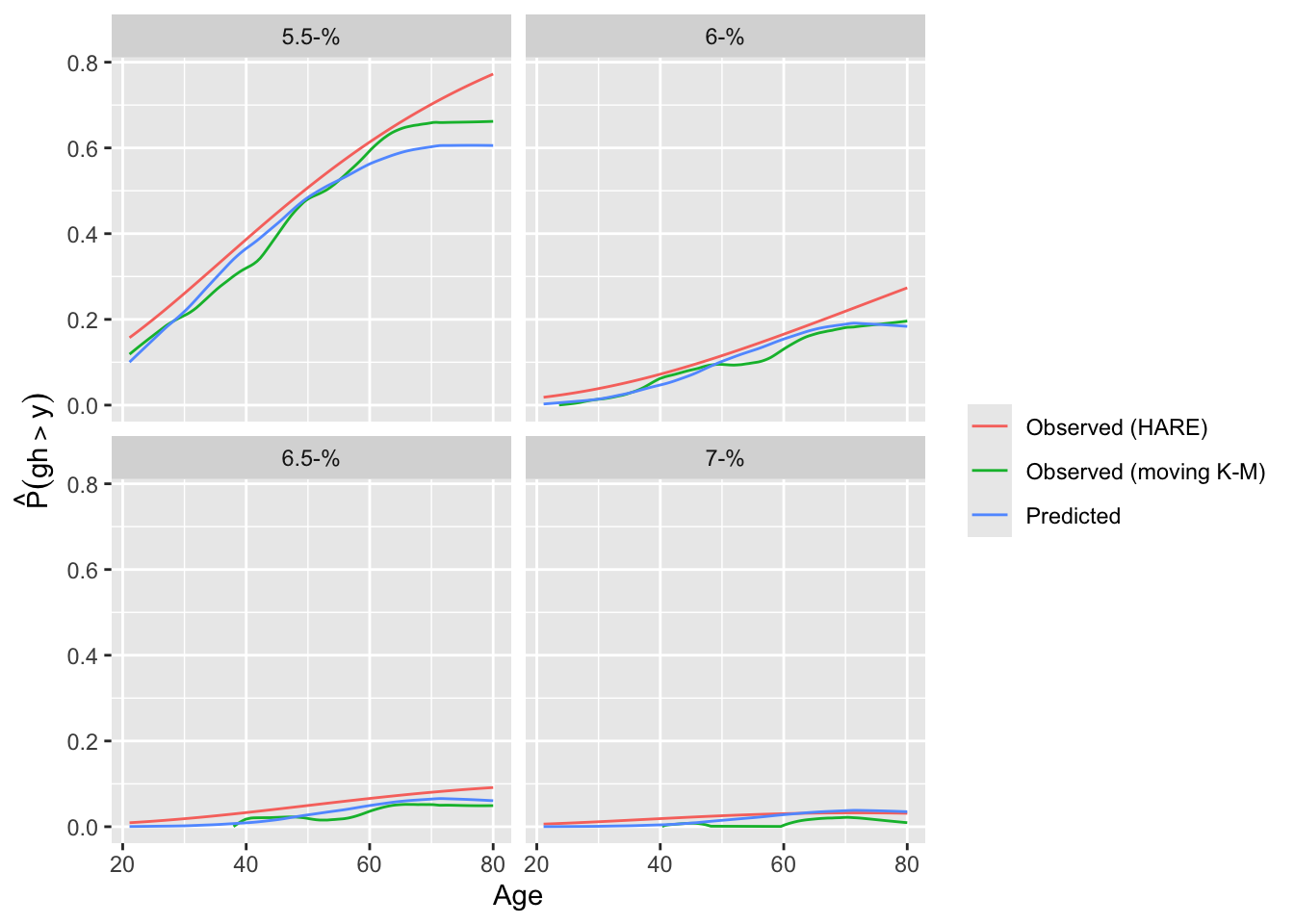
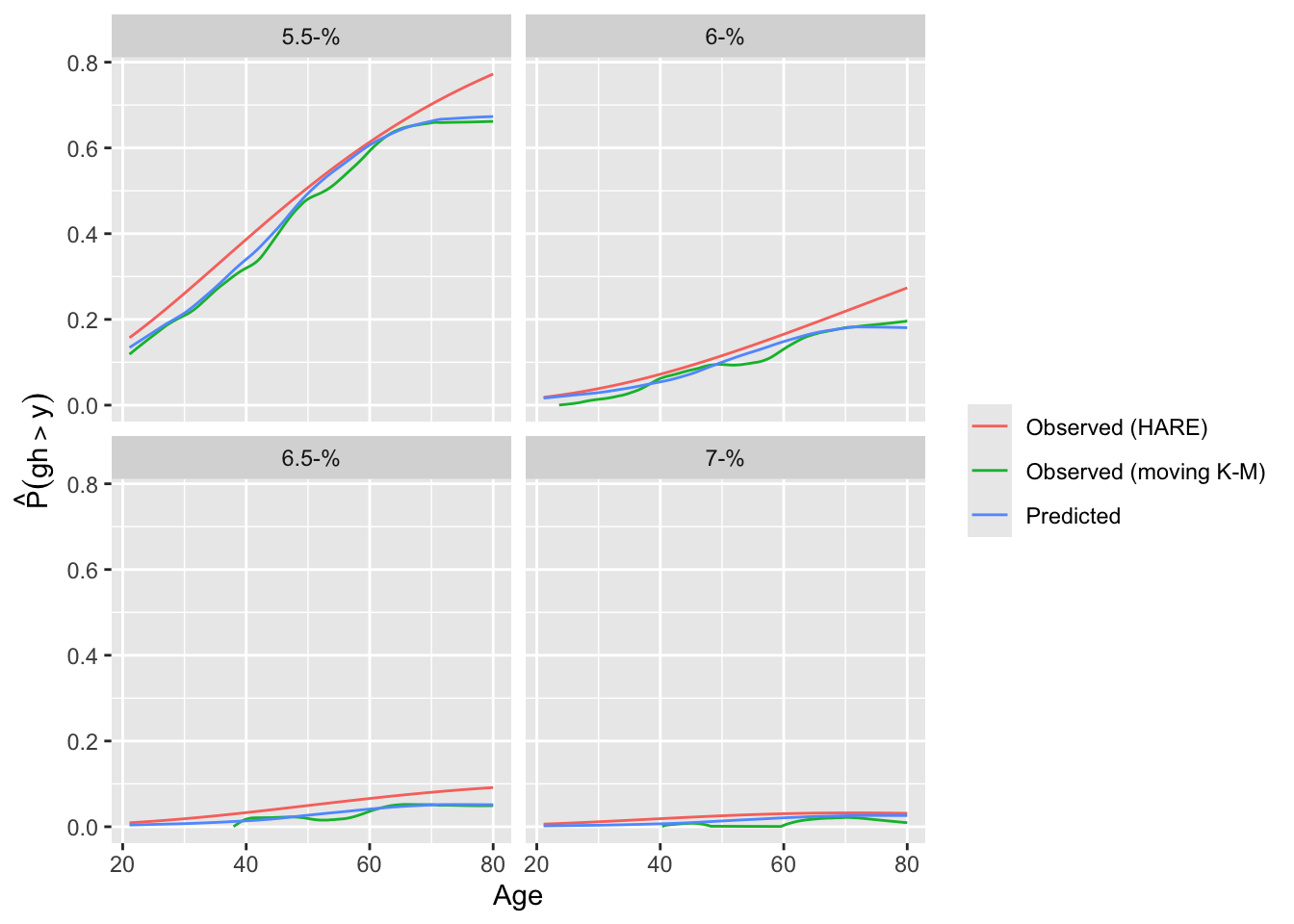
Finally, the rms Olinks function computes deviance measures for a series of link functions. Though this may not detect Y-dependency of effects (nonparallelism) with respect to a single predictor, it is useful for choosing the overall model. Model fits are automatically re-run by Olinks for a series of links not used in the current fit.
link null.deviance deviance AIC LR R2
1 loglog 26909.83 25580.57 25726.57 1329.262 0.249
2 logistic 26909.83 25522.82 25668.82 1387.005 0.258
3 probit 26909.83 25621.47 25767.47 1288.363 0.242
4 cloglog 26909.83 26096.27 26242.27 813.562 0.160Oddly, the logit link had the smallest deviance. More study of comparing deviances is needed.
Let \(\rho_{\tau}(y) = y(\tau - [y < 0])\). The \(\tau^{\mathrm th}\) sample quantile is the minimizer \(q\) of \(\sum_{i-1}^{n}\rho_{\tau}(y_{i}-q)\). For a conditional \(\tau^{\mathrm th}\) quantile of \(Y | X\) the corresponding quantile regression estimator \(\hat{\beta}_{\tau}\) minimizes \(\sum_{i=1}^{n}\rho_{\tau}(Y_{i}-X\beta)\). Quantile regression is not as efficient at estimating quantiles as is ordinary least squares at estimating the mean, if the latter’s assumptions hold. Koenker’s quantreg package in R (Koenker, 2009) implements quantile regression, and the rms package’s Rq function provides a front-end that gives rise to various graphics and inference tools. If we model the median gh as a function of covariates, only the \(X\beta\) structure need be correct. Other quantiles (e.g., \(90^\text{th}\) percentile) can be directly modeled but standard errors will be much larger as it is more difficult to precisely estimate outer quantiles.
3 For symmetric distributions applying a decreasing transformation will negate the coefficients. For asymmetric distributions (e.g., Gumbel), reversing the order of \(Y\) will do more than change signs.
4 Only an estimate of mean \(Y\) from these \(\hat{\beta}\)s is non-robust.
For a general continuous distribution function \(F(y)\), an ordinal regression model based on cumulative probabilities may be stated as follows5. Let the ordered unique values of \(Y\) be denoted by \(y_{1}, y_{2}, \dots, y_{k}\) and let the intercepts associated with \(y_{1}, \dots, y_{k}\) be \(\alpha_{1}, \alpha_{2}, \dots, \alpha_{k}\), where \(\alpha_{1} = \infty\) because \(\Pr[Y \geq y_{1}] = 1\). Let \(\alpha_{y} = \alpha_{i}, i:y_{i}=y\). Then \[ \Pr[Y \geq y_{i} | X] = F(\alpha_{i} + X\beta) = F(\alpha_{y_{i}} + X\beta) \] For the OLS fully parametric case, the model may be restated
5 It is more traditional to state the model in terms of \(\Pr[Y \leq y | X]\) but we use \(\Pr[Y \geq y | X]\) so that higher predicted values are associated with higher \(Y\).
so that to within an additive constant 6 \(\alpha_{y} = \frac{-y}{\sigma}\) (intercepts \(\alpha\) are linear in \(y\) whereas they are arbitrarily descending in the ordinal model), and \(\sigma\) is absorbed in \(\beta\) to put the OLS model into the new notation. The general ordinal regression model assumes that for fixed \(X_{1}, X_{2}\),
6 \(\hat{\alpha_{y}}\) are unchanged if a constant is added to all \(y\).
independent of the \(\alpha\)s (parallelism assumption). If \(F = [1 + \exp(-y)]^{-1}\), this is the proportional odds assumption.
Common choices of \(F\), implemented in the rms orm function, are shown in Table Table 15.1.
| Distribution | \(F\) | Inverse (Link Function) | Link Name | Connection |
|---|---|---|---|---|
| Logistic | \([1 + \exp(-y)]^{-1}\) | \(\log(\frac{y}{1-y})\) | logit | \(\frac{P_{2}}{1-P_{2}} = \frac{P_{1}}{1-P_{1}} \exp(\Delta)\) |
| Gaussian | \(\Phi(y)\) | \(\Phi^{-1}(y)\) | probit | \(P_{2}=\Phi(\Phi^{-1}(P_{1})+\Delta)\) |
| Gumbel maximum value | \(\exp(-\exp(-y))\) | \(\log(-\log(y))\) | \(\log-\log\) | \(P_{2}=P_{1}^{\exp(\Delta)}\) |
| Gumbel minimum value | \(1 - \exp(-\exp(y))\) | \(\log(-\log(1 - y))\) | complementary \(\log-\log\) | \(1-P_{2}=(1-P_{1})^{\exp(\Delta)}\) |
| Cauchy | \(\frac{1}{\pi}\tan^{-1}(y) + \frac{1}{2}\) | \(\tan[\pi(y - \frac{1}{2})]\) | cauchit |
The Gumbel maximum value distribution is also called the extreme value type I distribution. This distribution (\(\log-\log\) link) also represents a continuous time proportional hazards model. The hazard ratio when \(X\) changes from \(X_{1}\) to \(X_{2}\) is \(\exp(-(X_{2} -
X_{1}) \beta)\). The mean of \(Y | X\) is easily estimated by computing \[
\sum_{i=1}^{k} y_{i} \hat{\Pr}[Y = y_{i} | X]
\] and the \(q^\text{th}\) quantile of \(Y | X\) is \(y\) such that
\(F^{-1}(1 - q) - X\hat{\beta} = \hat{\alpha}_{y}\).7 The orm function in the rms package takes advantage of the information matrix being of a sparse tri-band diagonal form for the intercept parameters. This makes the computations efficient even for hundreds of intercepts (i.e., unique values of \(Y\)). orm is made to handle continuous \(Y\). Ordinal regression has nice properties in addition to those listed above, allowing for
7 The intercepts have to be shifted to the left one position in solving this equation because the quantile is such that \(\Pr[Y \leq y] = q\) whereas the model is stated in terms of \(\Pr[Y \geq y]\).
8 But it is not sensible to estimate quantiles of \(Y\) when there are heavy ties in \(Y\) in the area containing the quantile.
To summarize how assumptions of parametric models compare to assumptions of semiparametric models, consider the ordinary linear model or its special case the equal variance two-sample \(t\)-test, vs. the probit or logit (proportional odds) ordinal model or their special cases the Van der Waerden (normal-scores) two-sample test or the Wilcoxon test. All the assumptions of the linear model other than independence of residuals are captured in the following (written in traditional \(Y\leq y\) form):
spar(mfrow=c(1,2), left=2)
pinv <- expression(paste(Phi^{-1}, '(F(y', '|', 'X))'))
plot(0, 0, xlim=c(0, 1), ylim=c(-2, 2), type='n', axes=FALSE,
xlab=expression(y), ylab='')
mtext(pinv, side=2, line=1)
axis(1, labels=FALSE, lwd.ticks=0)
axis(2, labels=FALSE, lwd.ticks=0)
abline(a=-1.5, b=1)
abline(a=0, b=1)
arrows(.5, -1.5+.5, .5, 0+.5, code=3, length=.1)
text(.525, .5*(-1.5+.5+.5), expression(-Delta*X*beta/sigma), adj=0)
g <- function(x) -2.2606955+11.125231*x-37.772783*x^2+56.776436*x^3-
26.861103*x^4
x <- seq(0, .9, length=150)
pinv <- expression(atop(paste(Phi^{-1}, '(F(y', '|', 'X))'),
paste(logit, '(F(y', '|', 'X))')))
plot(0, 0, xlim=c(0, 1), ylim=c(-2, 2), type='n', axes=FALSE,
xlab=expression(y), ylab='')
mtext(pinv, side=2, line=1)
axis(1, labels=FALSE, lwd.ticks=FALSE)
axis(2, labels=FALSE, lwd.ticks=FALSE)
lines(x, g(x))
lines(x, g(x)+1.5)
arrows(.5, g(.5), .5, g(.5)+1.5, code=3, length=.1)
text(.525, .5*(g(.55) + g(.55)+1.5), expression(-Delta*X*beta), adj=0)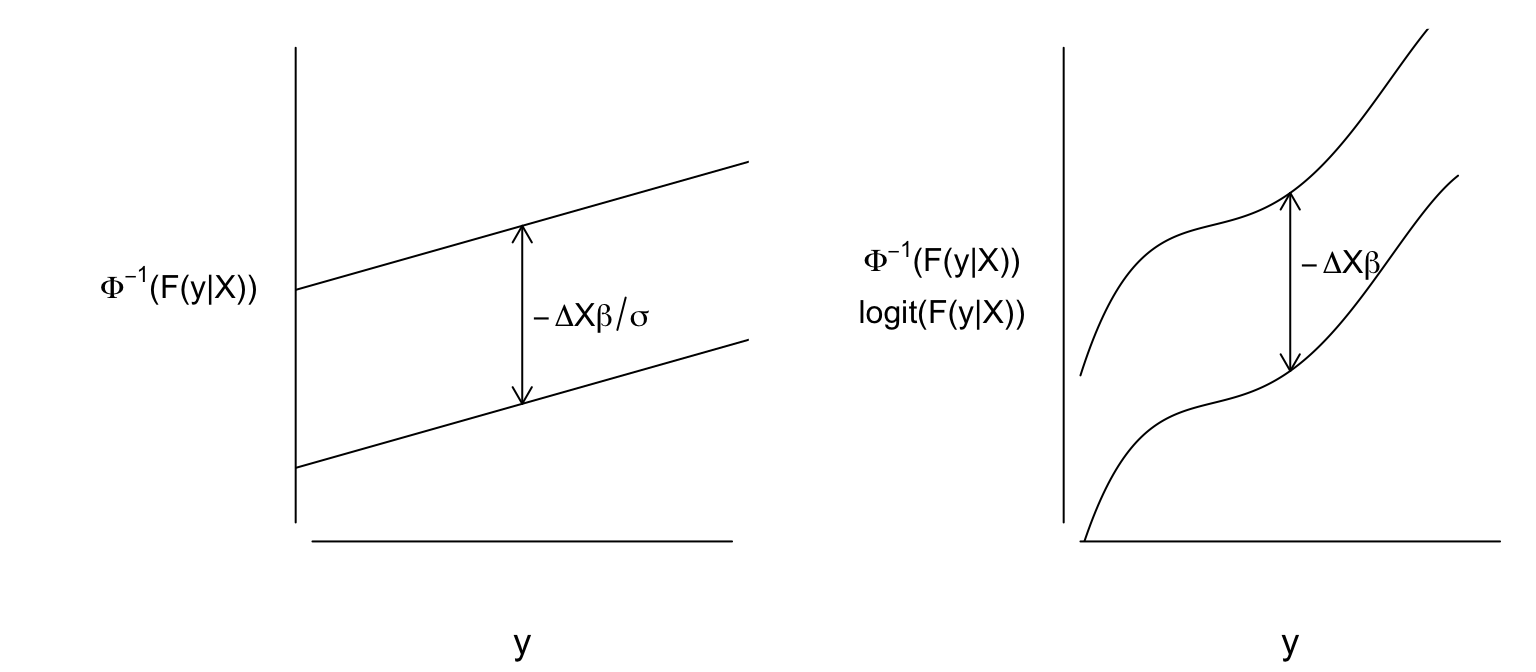
On the other hand, ordinal models assume the following: \[ \Pr[Y \leq y|X] = F(g(y)-X\beta), \] where \(g\) is unknown and may be discontinuous. From this point we revert back to \(Y\geq y\) notation so that \(Y\) increases as \(X\beta\) increases.
Global Modeling Implications
gh so use this link in an ordinal regression model (linearity of the curves is not required)Another way to examine model fit is to flexibly fit the single most important predictor (age) using a variety of methods, and comparing predictions to sample quantiles and means based on overlapping subsets on age, each subset being subjects having age \(< 5\) years away from the point being predicted by the models. Here we predict the 0.5, 0.75, and 0.9 quantiles and the mean. For quantiles we can compare to quantile regression(discussed below) and for means we compare to OLS.
require(data.table)
require(ggplot2)
estimands <- .q(q2, q3, p90, mean)
links <- .q(logistic, probit, loglog, cloglog)
estimators <- c(.q(empirical, ols, QR), links)
ages <- 25 : 75
nage <- length(ages)
yhat <- numeric(length(ages))
fmt <- function(x) format(round(x, 3), nsmall=3)
r <- expand.grid(estimand=estimands, estimator=estimators, age=ages,
y=NA_real_, stringsAsFactors=FALSE)
setDT(r)
# Discard irrelevant methods for estimands
r <- r[! (estimand == 'mean' & estimator == 'QR') &
! (estimand %in% .q(q2, q3, p90) & estimator == 'ols'), ]
# Find all used combinations
rc <- r[age == 25]
rc[, age := NULL]
mod <- gh ~ rcs(age,6)
# Compute estimates for all relevant combinations of estimands & estimators
for(eor in rc[, unique(estimator)]) {
if(eor == 'empirical') {
emp <- matrix(NA, nrow=nage, ncol=4,
dimnames=list(NULL, .q(mean, q2, q3, p90)))
for(j in 1 : length(ages)) {
s <- which(abs(w$age - ages[j]) < 5)
y <- w$gh[s]
a <- quantile(y, probs=c(0.5, 0.75, 0.90))
emp[j, ] <- c(mean(y), a)
}
}
else if(eor == 'ols') fit <- ols(mod, data=w)
else if(eor %in% links) fit <- orm(mod, data=w, family=eor)
for(eand in rc[estimator == eor, unique(estimand)]) {
qa <- switch(eand, q2=0.5, q3=0.75, p90=0.90)
yhat <- if(eor == 'ols') Predict(fit, age=ages, conf.int=FALSE)$yhat
else if(eor == 'empirical') emp[, eand]
else if(eor == 'QR') {
fit <- Rq(mod, data=w, tau=qa)
Predict(fit, age=ages, conf.int=FALSE)$yhat
}
else {
fun <- switch(eand,
mean = Mean(fit),
Quantile(fit))
fu <- if(eand == 'mean') fun
else function(x) fun(qa, x)
Predict(fit, age=ages, fun=fu, conf.int=FALSE)$yhat
}
r[estimand == eand & estimator == eor, y := yhat]
}
}
# Compute age-specific differences between estimates and empirical
# estimates, then compute mean absolute differences across all ages
dif <- r[estimator != 'empirical']
for(eor in rc[, setdiff(unique(estimator), 'empirical')])
for(eand in rc[estimator == eor, unique(estimand)])
dif[estimator == eor & estimand == eand]$y <-
r[estimator == eor & estimand == eand]$y -
r[estimator == 'empirical' & estimand == eand]$y
mad <- dif[, .(ad = mean(abs(y))), by=.(estimand, estimator)]
mad2 <- mad[, .(value = paste(fmt(ad), collapse='\n'),
label = paste(estimator, collapse='\n'),
x = if(estimand == 'p90') 60 else 25,
y = if(estimand == 'p90') 5.5 else 6.2),
by=.(estimand)]
ggplot() + geom_line(aes(x=age, y=y, col=estimator),
data=r[estimator != 'empirical']) +
geom_point(aes(x=age, y=y, alpha=I(0.35)),
data=r[estimator == 'empirical']) +
facet_wrap(~ estimand) +
geom_text(aes(x=x, y=y, label=label, hjust='left', size=I(3)), data=mad2) +
geom_text(aes(x=x+10, y=y, label=value, hjust='left', size=I(3)), data=mad2) +
guides(color=guide_legend(title='')) +
theme(legend.position='bottom')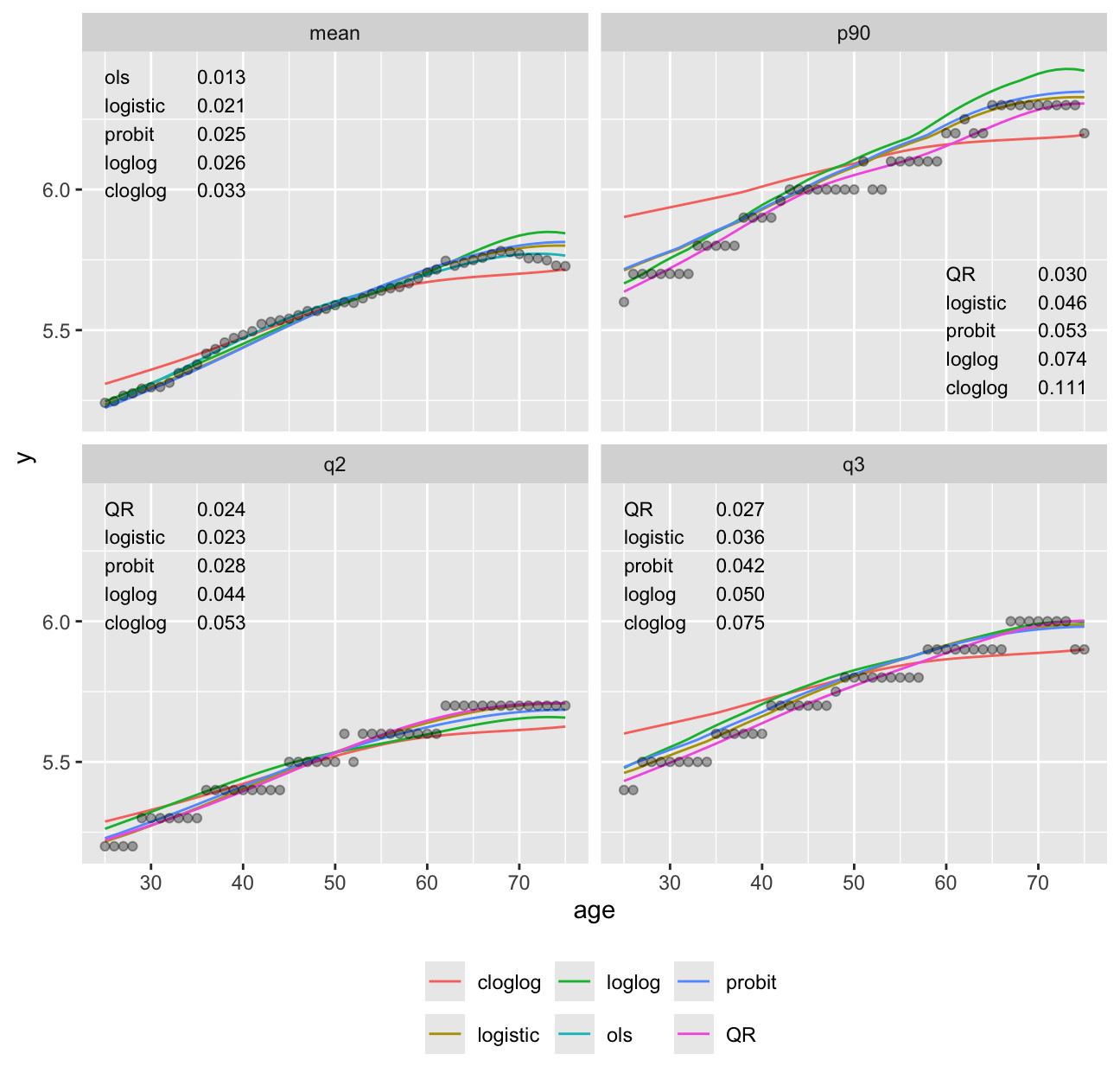
It can be seen in Figure 15.3 that models dedicated to a specific task (quantile regression for quantiles and OLS for means) were best for those tasks. Although the log-log ordinal cumulative probability model did not estimate the median as accurately as some other methods, it does well for the 0.75 and 0.9 quantiles and is the best compromise overall because of its ability to also directly predict the mean as well as quantities such as \(\Pr[\text{HbA}_{1c} > 7 | X]\). For here on we focus on the log-log ordinal model. Going back to the bottom left of Figure 15.1, let’s look at quantile groups of predicted \(\text{HbA}_{1c}\) by OLS and plot predicted distributions of actual \(\text{HbA}_{1c}\) against empirical distributions.
###w$pghg <- cut2(pgh, g=6)
f <- orm(gh ~ pgh6, family='loglog', data=w)
lp <- predict(f, newdata=data.frame(pgh6=levels(w$pgh6)))
ep <- ExProb(f) # Exceedance prob. functn. generator in rms
z <- ep(lp)
j <- order(w$pgh6) # puts in order of lp (levels of pghg)
plot(z, xlim=c(4, 7.5), data=w[j,c('pgh6', 'gh')]) 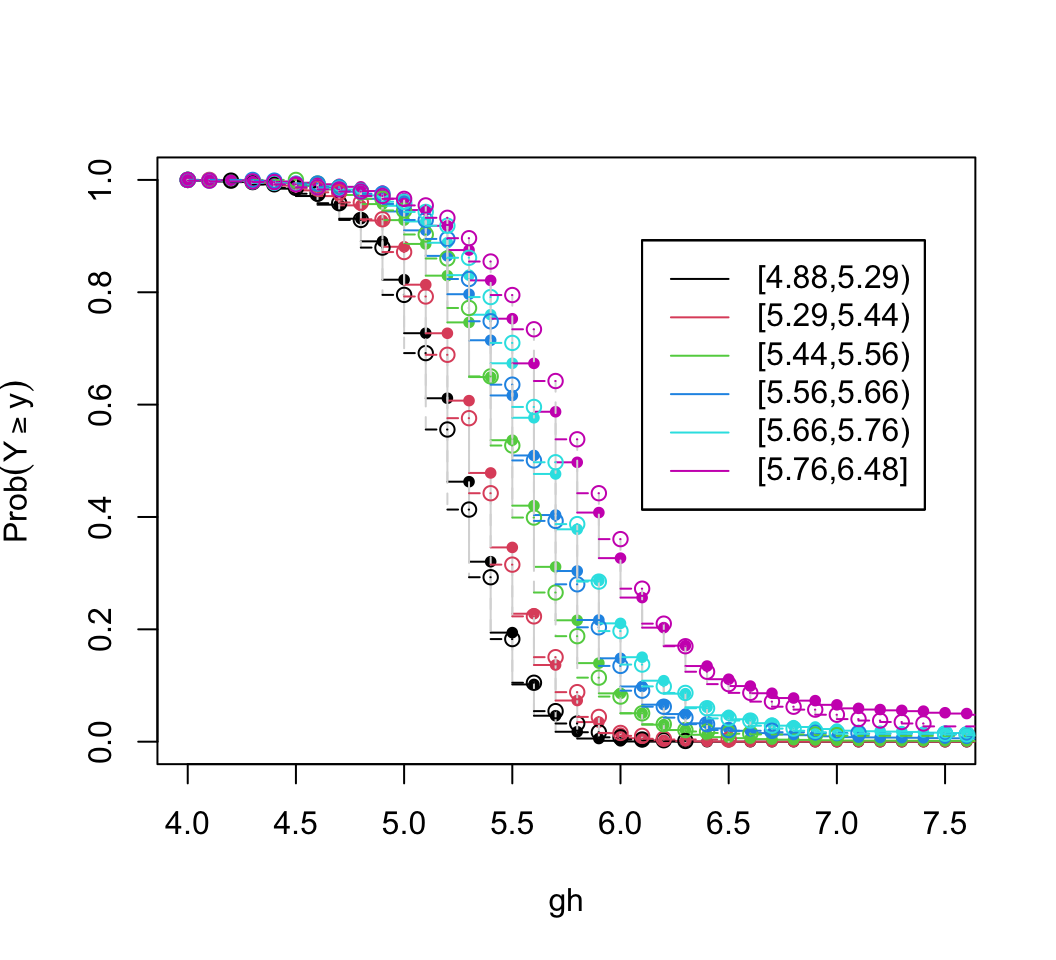
Agreement between predicted and observed exceedance probability distributions is excellent in Figure 15.4. To return to the initial look at a linear model with assumed Gaussian residuals, fit a probit ordinal model and compare the estimated intercepts to the linear relationship with gh that is assumed by the normal distribution.
spar(bty='l')
f <- orm(gh ~ rcs(age,6), family='probit', data=w)
g <- ols(gh ~ rcs(age,6), data=w)
s <- g$stats['Sigma']
yu <- f$yunique[-1]
r <- quantile(w$gh, c(.005, .995))
alphas <- coef(f)[1:num.intercepts(f)]
plot(-yu / s, alphas, type='l', xlim=rev(- r / s),
xlab=expression(-y/hat(sigma)), ylab=expression(alpha[y]))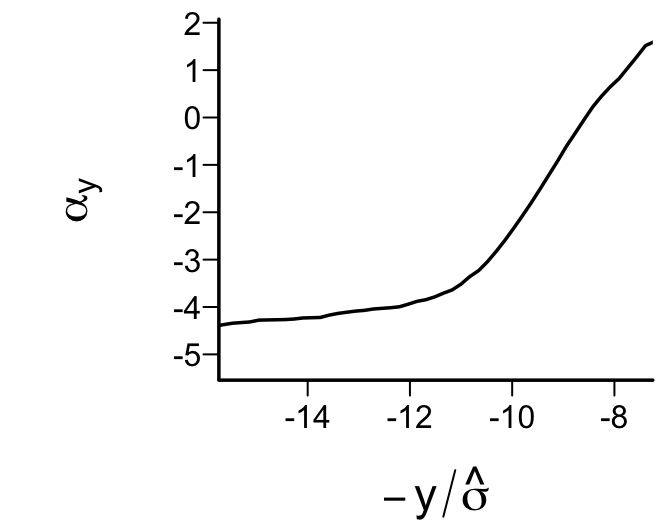
Figure 15.5 depicts a significant departure from that implied by Gaussian residuals.
Using the log-log model, we first check the adequacy of BMI as a summary of height and weight for estimating median gh.
-log-log Ordinal Regression Model
orm(formula = gh ~ rcs(age, 5) + log(ht) + log(wt), data = w,
family = "loglog")
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 4629 | LR χ2 1126.94 | R2 0.217 | ρ 0.486 |
| ESS 4602.2 | d.f. 6 | R26,4629 0.215 | Dxy 0.359 |
| Distinct Y 63 | Pr(>χ2) <0.0001 | R26,4602.2 0.216 | |
| Y0.5 5.5 | Score χ2 1262.81 | |Pr(Y ≥ median)-½| 0.153 | |
| max |∂log L/∂β| 2×10-10 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| age | 0.0398 | 0.0055 | 7.29 | <0.0001 |
| age' | -0.0158 | 0.0275 | -0.57 | 0.5657 |
| age'' | -0.0072 | 0.0866 | -0.08 | 0.9333 |
| age''' | 0.0309 | 0.1135 | 0.27 | 0.7853 |
| ht | -3.0680 | 0.2789 | -11.00 | <0.0001 |
| wt | 1.2748 | 0.0704 | 18.10 | <0.0001 |
[1] 25910.77 25910.17 25906.03The ratio of the coefficient of log height to the coefficient of log weight is -2.4, which is between what BMI uses and the more dimensionally reasonable weight / height\(^{3}\). By AIC, a spline interaction surface between height and weight does slightly better than BMI in predicting \(\text{HbA}_{1c}\), but a nonlinear function of BMI is barely worse. It will require other body size measures to displace BMI as a predictor. As an aside, compare this model fit to that from the Cox proportional hazards model. The Cox model uses a conditioning argument to obtain a partial likelihood free of the intercepts \(\alpha\) (and requires a second step to estimate these log discrete hazard components) whereas we are using a full marginal likelihood of the ranks of \(Y\) (Kalbfleisch & Prentice, 1973).
Cox Proportional Hazards Model
cph(formula = Surv(gh) ~ rcs(age, 5) + log(ht) + log(wt), data = w)
| Model Tests | Discrimination Indexes |
|
|---|---|---|
| Obs 4629 | LR χ2 1120.20 | R2 0.215 |
| Events 4629 | d.f. 6 | R26,4629 0.214 |
| Center 8.3792 | Pr(>χ2) 0.0000 | Dxy 0.359 |
| Score χ2 1258.07 | ||
| Pr(>χ2) 0.0000 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| age | -0.0392 | 0.0054 | -7.24 | <0.0001 |
| age' | 0.0148 | 0.0274 | 0.54 | 0.5888 |
| age'' | 0.0093 | 0.0862 | 0.11 | 0.9144 |
| age''' | -0.0321 | 0.1131 | -0.28 | 0.7767 |
| ht | 3.0477 | 0.2779 | 10.97 | <0.0001 |
| wt | -1.2653 | 0.0701 | -18.04 | <0.0001 |
Back up and look at all body size measures, and examine their redundancies.
Redundancy Analysis
~ht + bmi + leg + arml + armc + waist + tri + sub
n: 3853 p: 8 nk: 3
Number of NAs: 0
Transformation of target variables forced to be linear
R-squared cutoff: 0.75 Type: ordinary
R^2 with which each variable can be predicted from all other variables:
ht bmi leg arml armc waist tri sub
0.829 0.924 0.682 0.748 0.843 0.864 0.531 0.594
Rendundant variables:
bmi ht
Predicted from variables:
leg arml armc waist tri sub
Variable Deleted R^2 R^2 after later deletions
1 bmi 0.924 0.909
2 ht 0.792
Strongest Predictors of Each Variable With Cumulative R^2
ht
arml (0.658) + leg (0.765) + tri (0.786) + waist (0.788) + bmi (0.807)
bmi
waist (0.775) + armc (0.839) + ht (0.913) + tri (0.916) + leg (0.916)
leg
ht (0.632) + waist (0.646) + arml (0.663) + bmi (0.676) + tri (0.679)
arml
ht (0.658) + waist (0.721) + leg (0.735) + armc (0.738) + tri (0.742)
armc
bmi (0.716) + ht (0.814) + waist (0.821) + arml (0.824) + sub (0.828)
waist
bmi (0.775) + ht (0.828) + leg (0.84) + arml (0.845) + armc (0.851)
tri
sub (0.399) + ht (0.487) + bmi (0.518) + waist (0.522) + arml (0.524)
sub
bmi (0.464) + tri (0.558) + waist (0.568) + armc (0.573) + ht (0.573)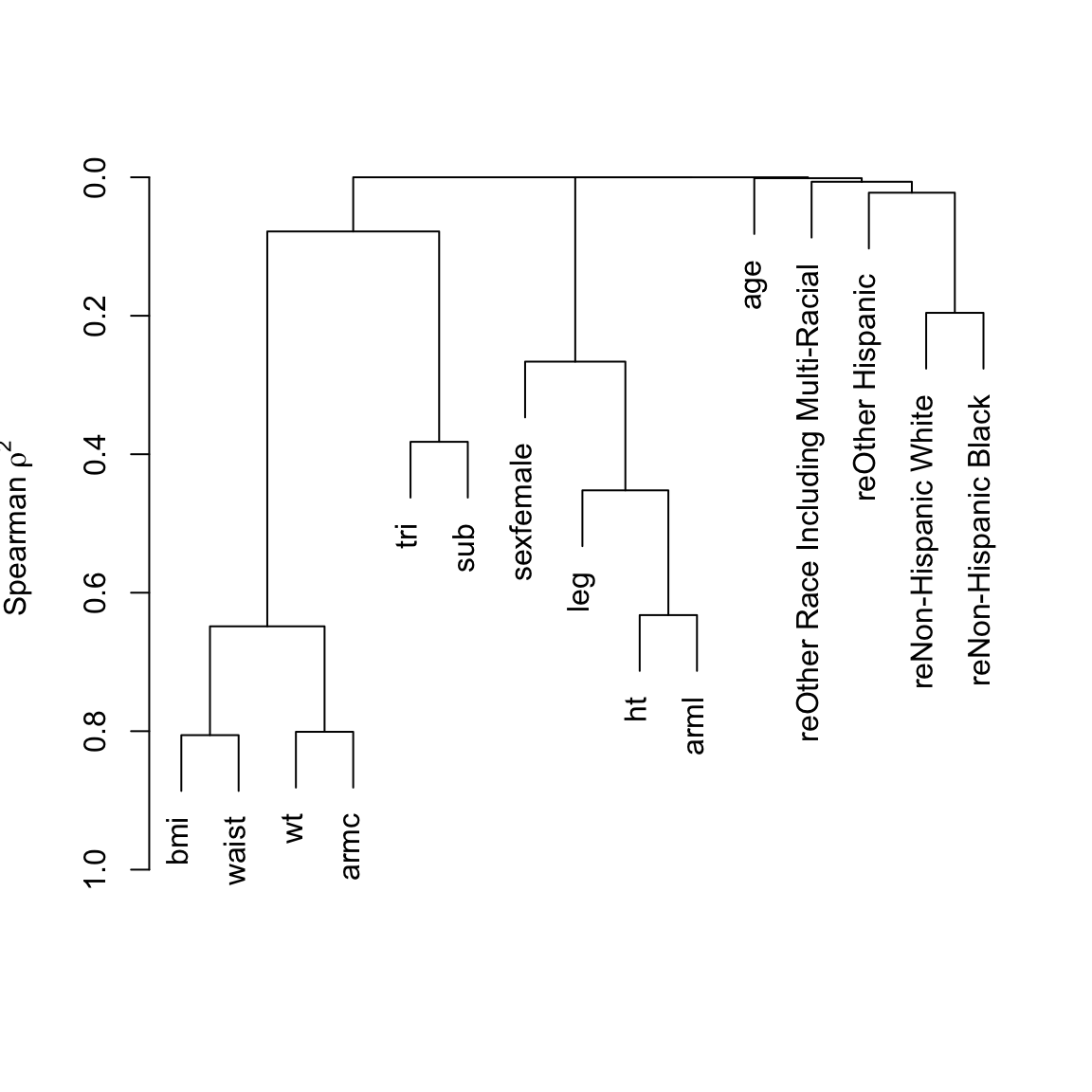
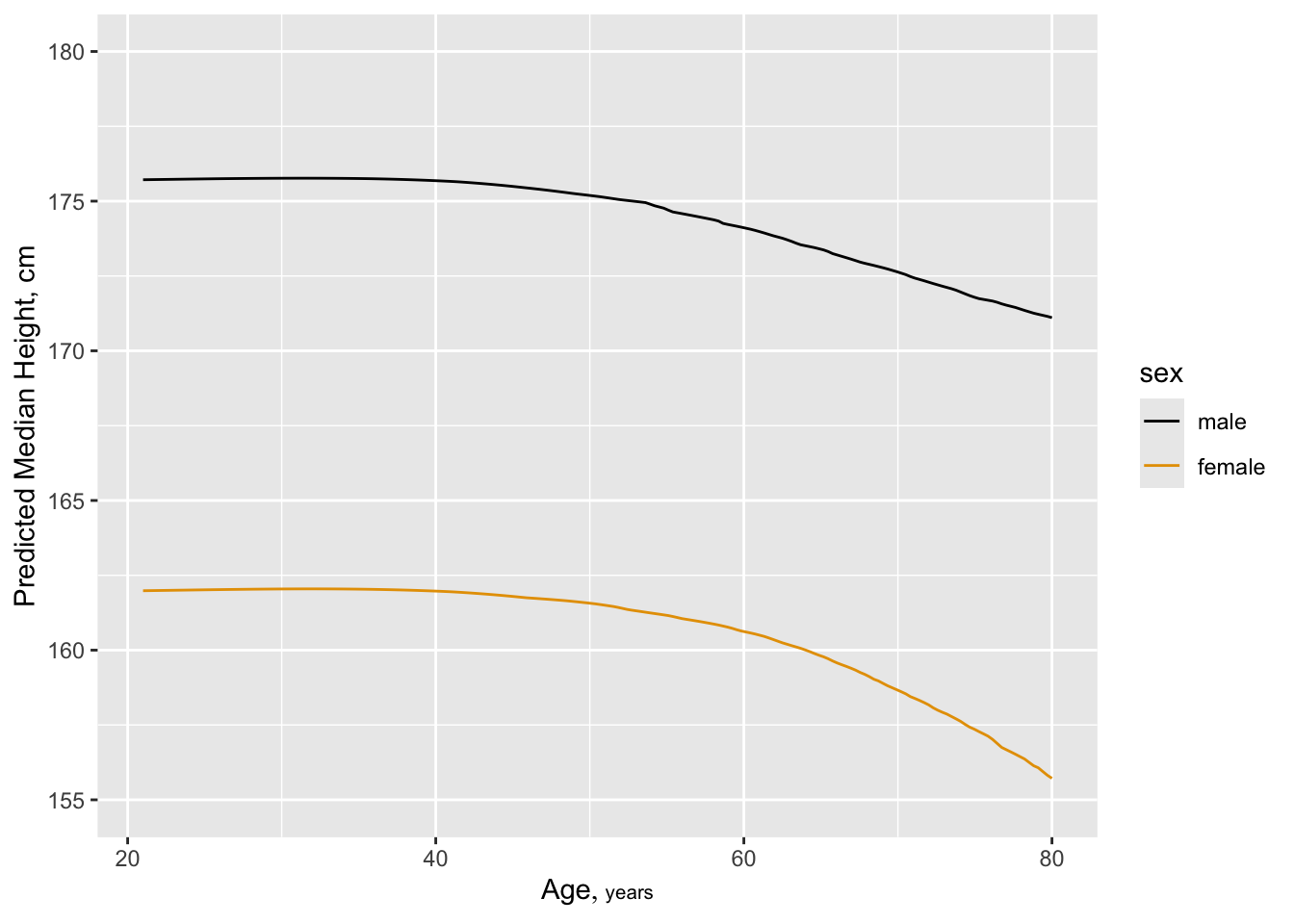
Six size measures adequately capture the entire set. Height and BMI are removed. An advantage of removing height is that it is age-dependent in the elderly:
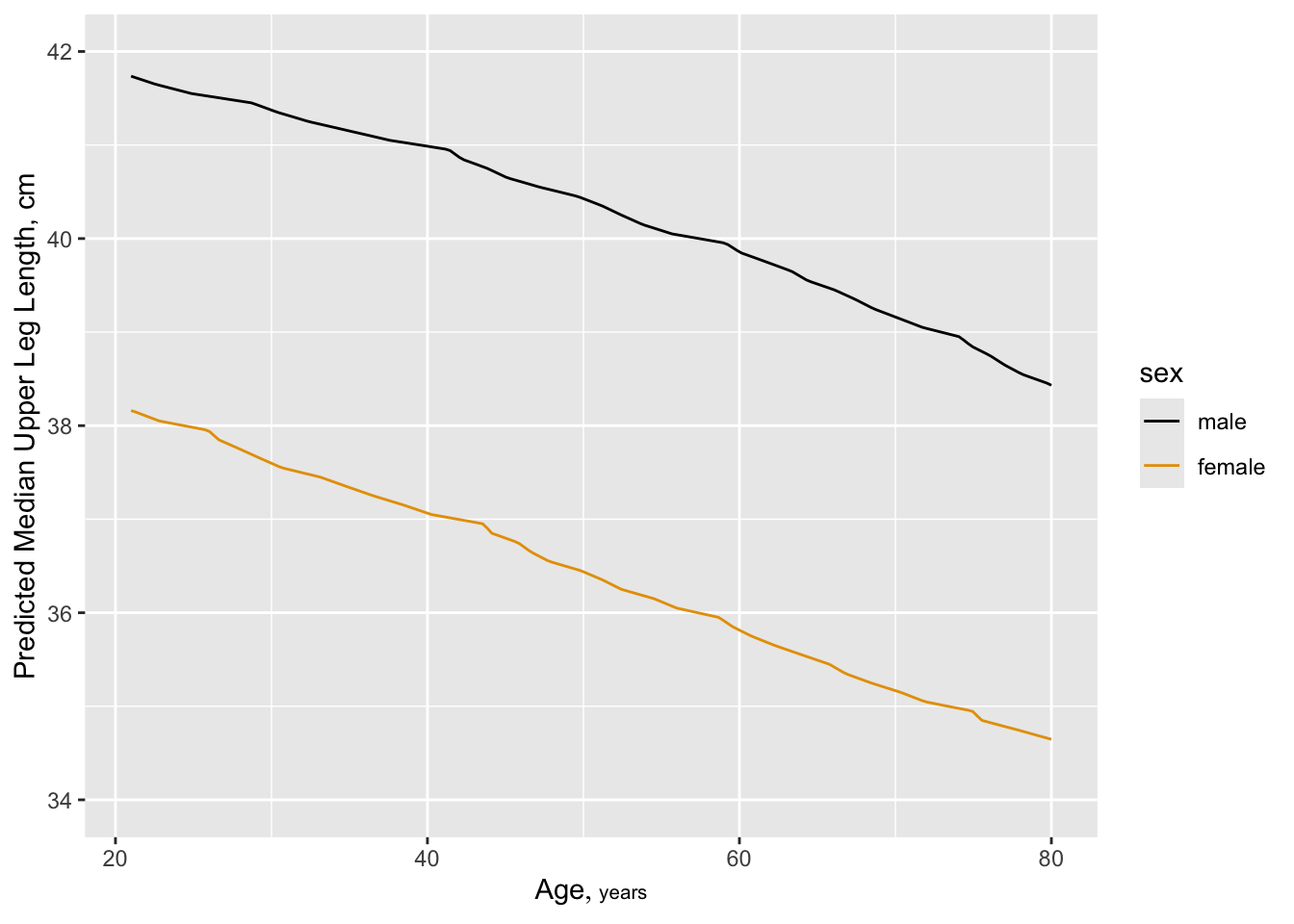
But also see a change in leg length:
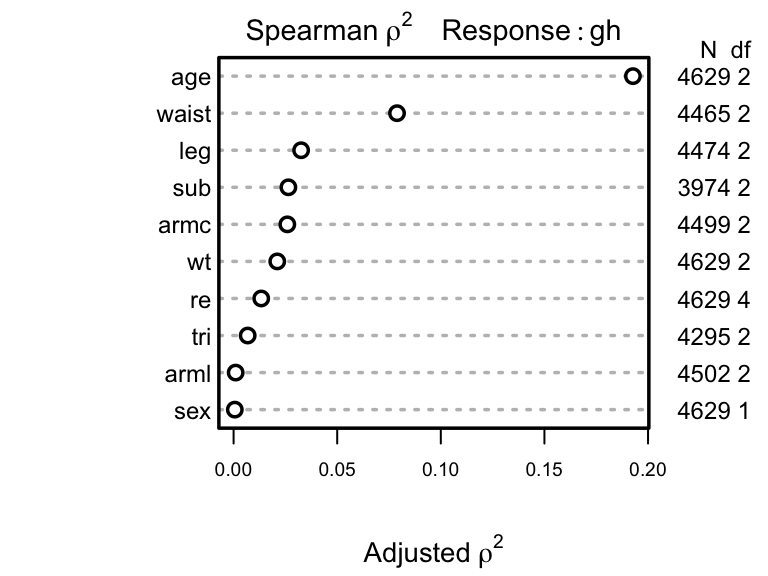
Next allocate d.f. according to generalized Spearman
\(\rho^{2}\) 9.
9 Competition between collinear size measures hurts interpretation of partial tests of association in a saturated additive model.
Parameters will be allocated in descending order of \(\rho^2\). But note that subscapular skinfold has a large number of NAs and other predictors also have NAs. Suboptimal casewise deletion will be used until the final model is fitted. Because there are many competing body measures, we use backwards stepdown to arrive at a set of predictors. The bootstrap will be used to penalize predictive ability for variable selection. First the full model is fit using casewise deletion, then we do a composite test to assess whether any of the frequently-missing predictors is important. Use likelihood ratio \(\chi^2\) tests.
-log-log Ordinal Regression Model
orm(formula = gh ~ rcs(age, 5) + sex + re + rcs(wt, 3) + rcs(leg,
3) + arml + rcs(armc, 3) + rcs(waist, 4) + tri + rcs(sub,
3), data = w, family = "loglog", x = TRUE, y = TRUE)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 3853 | LR χ2 1180.13 | R2 0.265 | ρ 0.520 |
| ESS 3829.2 | d.f. 22 | R222,3853 0.260 | Dxy 0.388 |
| Distinct Y 60 | Pr(>χ2) <0.0001 | R222,3829.2 0.261 | |
| Y0.5 5.5 | Score χ2 1298.88 | |Pr(Y ≥ median)-½| 0.172 | |
| max |∂log L/∂β| 7×10-11 | Pr(>χ2) <0.0001 |
Likelihood Ratio Statistics for gh |
|||
| χ2 | d.f. | P | |
|---|---|---|---|
| leg | 8.44 | 2 | 0.0147 |
| Nonlinear | 3.36 | 1 | 0.0668 |
| arml | 0.16 | 1 | 0.6925 |
| armc | 6.63 | 2 | 0.0364 |
| Nonlinear | 3.27 | 1 | 0.0707 |
| waist | 29.48 | 3 | <0.0001 |
| Nonlinear | 4.30 | 2 | 0.1165 |
| tri | 16.50 | 1 | <0.0001 |
| sub | 41.53 | 2 | <0.0001 |
| Nonlinear | 4.53 | 1 | 0.0334 |
| TOTAL NONLINEAR | 15.04 | 5 | 0.0102 |
| TOTAL | 130.04 | 11 | <0.0001 |
The model yields Spearman \(\rho=0.52\), the rank correlation between predicted and observed \(\text{HbA}_{1c}\). Show predicted mean and median \(\text{HbA}_{1c}\) as a function of age, adjusting other variables to median/mode. Compare the estimate of the median with that from quantile regression (discussed below).
M <- Mean(f)
qu <- Quantile(f)
med <- function(x) qu(.5, x)
p90 <- function(x) qu(.9, x)
fq <- Rq(formula(f), data=w)
fq90 <- Rq(formula(f), data=w, tau=.9)
pmean <- Predict(f, age, fun=M, conf.int=FALSE)
pmed <- Predict(f, age, fun=med, conf.int=FALSE)
p90 <- Predict(f, age, fun=p90, conf.int=FALSE)
pmedqr <- Predict(fq, age, conf.int=FALSE)
p90qr <- Predict(fq90, age, conf.int=FALSE)
z <- rbind('orm mean'=pmean, 'orm median'=pmed, 'orm P90'=p90,
'QR median'=pmedqr, 'QR P90'=p90qr)
ggplot(z, groups='.set.',
adj.subtitle=FALSE, legend.label=FALSE)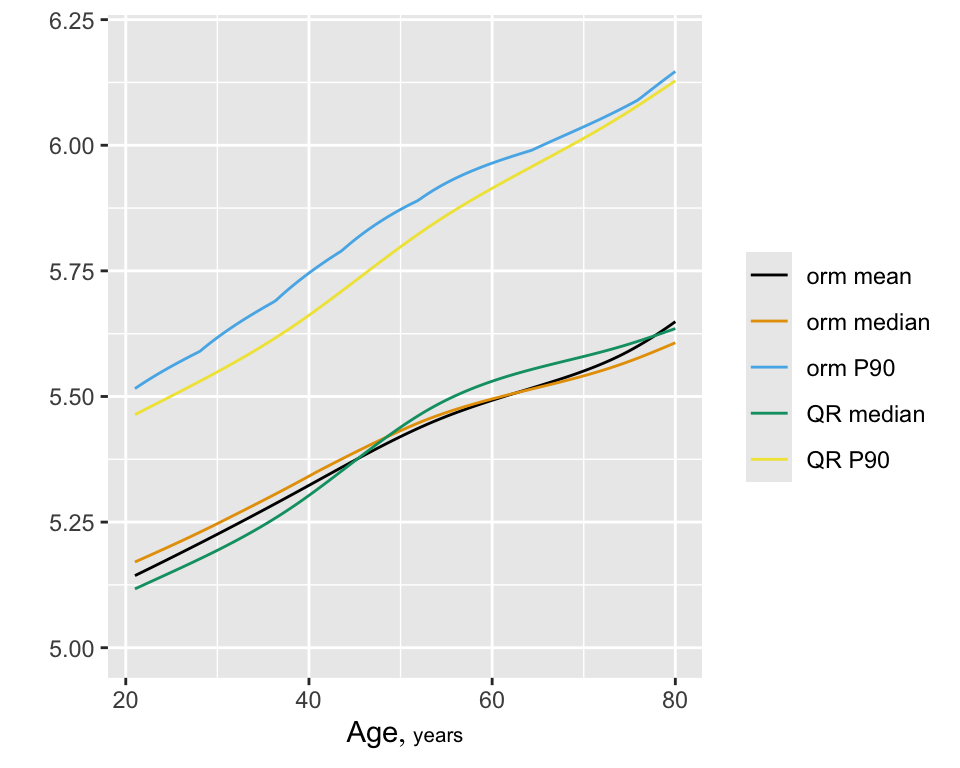
Next do fast backward step-down in an attempt to get a model without so much competition among variables. The stepwise selection will be penalized for in the model validation.
Deleted Chi-Sq d.f. P Residual d.f. P AIC
arml 0.16 1 0.6924 0.16 1 0.6924 -1.84
sex 0.45 1 0.5019 0.61 2 0.7381 -3.39
wt 5.72 2 0.0572 6.33 4 0.1759 -1.67
armc 3.32 2 0.1897 9.65 6 0.1400 -2.35
Factors in Final Model
[1] age re leg waist tri sub Validate the model, properly penalizing for variable selection
| Index | Original Sample |
Training Sample |
Test Sample |
Optimism | Corrected Index |
Lower | Upper | Successful Resamples |
|---|---|---|---|---|---|---|---|---|
| ρ | 0.5172 | 0.5209 | 0.5149 | 0.006 | 0.5112 | 0.4887 | 0.5366 | 100 |
| Dxy | 0.3861 | 0.3893 | 0.3842 | 0.005 | 0.3811 | 0.3643 | 0.4006 | 100 |
| R2 | 0.2629 | 0.2686 | 0.2592 | 0.0094 | 0.2535 | 0.2359 | 0.2763 | 100 |
| Slope | 1 | 1 | 0.9772 | 0.0228 | 0.9772 | 0.9263 | 1.0319 | 100 |
| g | 0.7289 | 0.7401 | 0.7218 | 0.0183 | 0.7106 | 0.6785 | 0.7615 | 100 |
| Mean |Pr(Y≥Y0.5)-0.5| | 0.172 | 0.176 | 0.1702 | 0.0058 | 0.1662 | 0.1609 | 0.1836 | 100 |
| Factors Retained in Backwards Elimination First 30 Resamples |
|||||||||
| age | sex | re | wt | leg | arml | armc | waist | tri | sub |
|---|---|---|---|---|---|---|---|---|---|
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| Frequencies of Numbers of Factors Retained | ||||
| 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|
| 1 | 33 | 41 | 21 | 4 |
Develop multiple imputations then repeat the bootstrap validation process, but separately for each completed dataset. The overall validation averages the bootstrap-corrected model performance measures over five validations.
Multiple Imputation using Bootstrap and PMM
aregImpute(formula = ~gh + age + sex + re + wt + leg + arml +
armc + waist + tri + sub, data = w, n.impute = 5, pr = FALSE)
n: 4629 p: 11 Imputations: 5 nk: 3
Number of NAs:
gh age sex re wt leg arml armc waist tri sub
0 0 0 0 0 155 127 130 164 334 655
type d.f.
gh s 2
age s 2
sex c 1
re c 4
wt s 2
leg s 2
arml s 2
armc s 2
waist s 2
tri s 2
sub s 1
Transformation of Target Variables Forced to be Linear
R-squares for Predicting Non-Missing Values for Each Variable
Using Last Imputations of Predictors
leg arml armc waist tri sub
0.638 0.720 0.862 0.904 0.746 0.641 v <- function(fit)
list(validate=validate(fit, B=100, bw=TRUE, estimates=FALSE,
prmodsel=FALSE, rule='p', pr=FALSE))
h <- function()
fit.mult.impute(gh ~ rcs(age,5) + sex + re + rcs(wt,3) + rcs(leg,3) + arml +
rcs(armc,3) + rcs(waist,4) + tri + rcs(sub,3),
orm, a, data=w,
fun=v, fitargs=list(x=TRUE, y=TRUE, family='loglog'), pr=FALSE)
f <- runifChanged(h, a, v) # 11m
print(processMI(f, 'validate'), B=10, digits=3)| Index | Original Sample |
Training Sample |
Test Sample |
Optimism | Corrected Index |
Lower | Upper | Successful Resamples |
|---|---|---|---|---|---|---|---|---|
| ρ | 0.513 | 0.515 | 0.511 | 0.004 | 0.508 | 0.49 | 0.533 | 500 |
| Dxy | 0.384 | 0.386 | 0.382 | 0.004 | 0.38 | 0.366 | 0.399 | 500 |
| R2 | 0.268 | 0.273 | 0.266 | 0.007 | 0.261 | 0.246 | 0.286 | 500 |
| Slope | 1 | 1 | 0.981 | 0.019 | 0.981 | 0.93 | 1.028 | 500 |
| g | 0.741 | 0.749 | 0.734 | 0.015 | 0.726 | 0.697 | 0.775 | 500 |
| Mean |Pr(Y≥Y0.5)-0.5| | 0.173 | 0.174 | 0.171 | 0.003 | 0.17 | 0.163 | 0.179 | 500 |
| Factors Retained in Backwards Elimination First 10 Resamples |
|||||||||
| age | sex | re | wt | leg | arml | armc | waist | tri | sub |
|---|---|---|---|---|---|---|---|---|---|
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ||||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |||
| ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | ⚬ | |
| Frequencies of Numbers of Factors Retained | |||||
| 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|
| 1 | 38 | 31 | 22 | 7 | 1 |
There is no calibrate method for orm model fits.
Next fit the reduced model. Use multiple imputation to impute missing predictors. Do a LR ANOVA for the reduced model, taking imputation into account.
-log-log Ordinal Regression Model
fit.mult.impute(formula = gh ~ rcs(age, 5) + re + rcs(leg, 3) +
rcs(waist, 4) + tri + rcs(sub, 4), fitter = orm, xtrans = a,
data = w, lrt = TRUE, pr = FALSE, fitargs = list(family = "loglog"))
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 4629 | LR χ2 1443.45 | R2 0.269 | ρ 0.512 |
| ESS 23011.2 | d.f. 17 | R217,23145 0.267 | Dxy 0.383 |
| Distinct Y 63 | Pr(>χ2) <0.0001 | R217,23011.2 0.269 | |
| Y0.5 5.5 | Score χ2 7820.99 | |Pr(Y ≥ median)-½| 0.173 | |
| max |∂log L/∂β| 1×10-10 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| age | 0.0405 | 0.0055 | 7.35 | <0.0001 |
| age' | -0.0226 | 0.0277 | -0.82 | 0.4146 |
| age'' | 0.0114 | 0.0871 | 0.13 | 0.8958 |
| age''' | 0.0448 | 0.1145 | 0.39 | 0.6958 |
| re=Other Hispanic | -0.0703 | 0.0592 | -1.19 | 0.2345 |
| re=Non-Hispanic White | -0.4128 | 0.0450 | -9.18 | <0.0001 |
| re=Non-Hispanic Black | 0.0635 | 0.0562 | 1.13 | 0.2589 |
| re=Other Race Including Multi-Racial | -0.0434 | 0.0746 | -0.58 | 0.5607 |
| leg | -0.0324 | 0.0092 | -3.51 | 0.0004 |
| leg' | 0.0138 | 0.0107 | 1.28 | 0.1988 |
| waist | 0.0076 | 0.0050 | 1.52 | 0.1283 |
| waist' | 0.0305 | 0.0161 | 1.90 | 0.0576 |
| waist'' | -0.0916 | 0.0522 | -1.76 | 0.0790 |
| tri | -0.0159 | 0.0026 | -6.04 | <0.0001 |
| sub | -0.0026 | 0.0097 | -0.27 | 0.7881 |
| sub' | 0.0635 | 0.0307 | 2.07 | 0.0386 |
| sub'' | -0.1694 | 0.0999 | -1.70 | 0.0898 |
| Imputation penalties | |||
| Test | Missing Information Fraction |
Denominator d.f. |
χ2 Discount |
|---|---|---|---|
| age | 0.095 | 1760.5 | 0.905 |
| Nonlinear | 0.033 | 11155.4 | 0.967 |
| re | 0.000 | Inf | 1.000 |
| leg | 0.003 | 914800.9 | 0.997 |
| Nonlinear | 0.071 | 788.9 | 0.929 |
| waist | 0.000 | Inf | 1.000 |
| Nonlinear | 0.030 | 8609.4 | 0.970 |
| tri | 0.155 | 166.0 | 0.845 |
| sub | 0.301 | 132.9 | 0.699 |
| Nonlinear | 0.286 | 98.0 | 0.714 |
| TOTAL NONLINEAR | 0.100 | 3197.8 | 0.900 |
| TOTAL | 0.074 | 12487.9 | 0.926 |
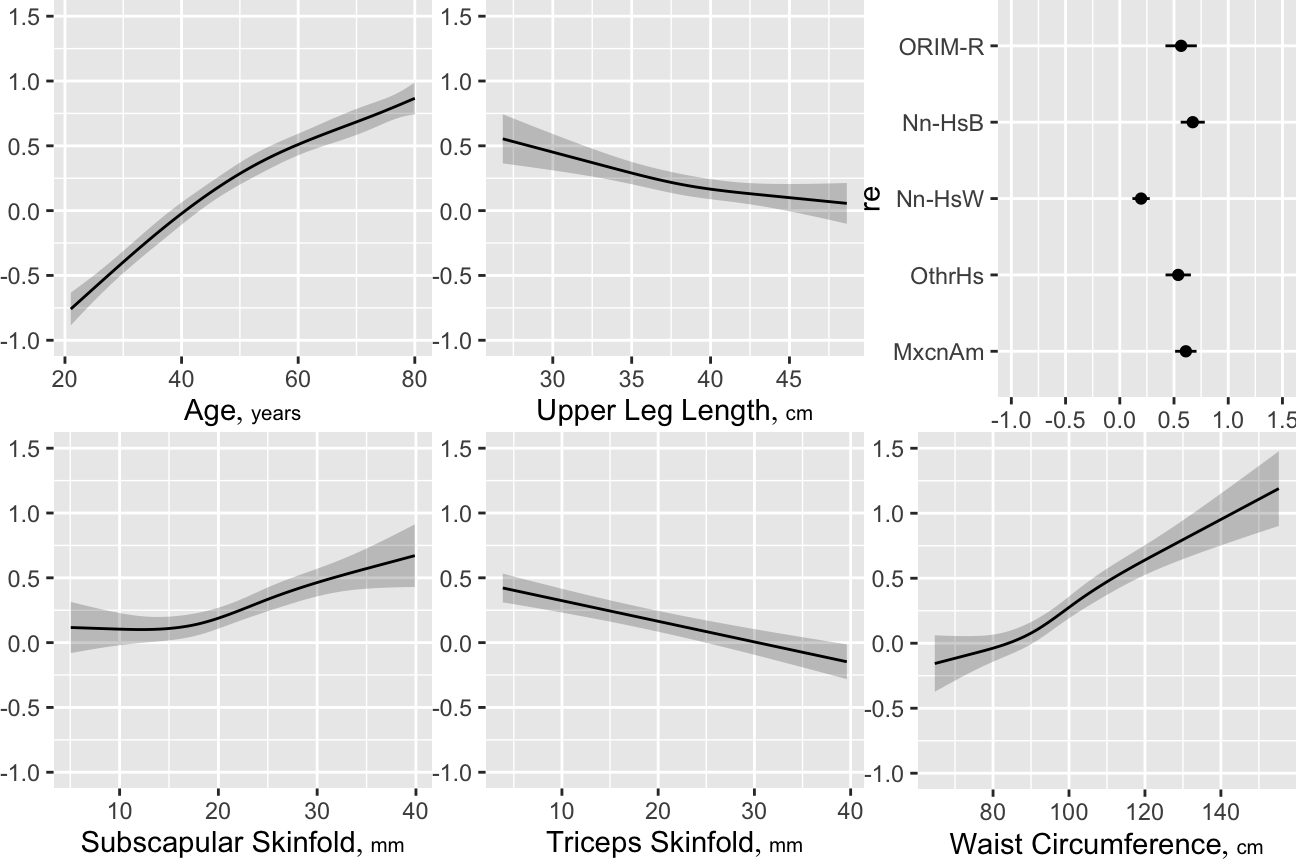
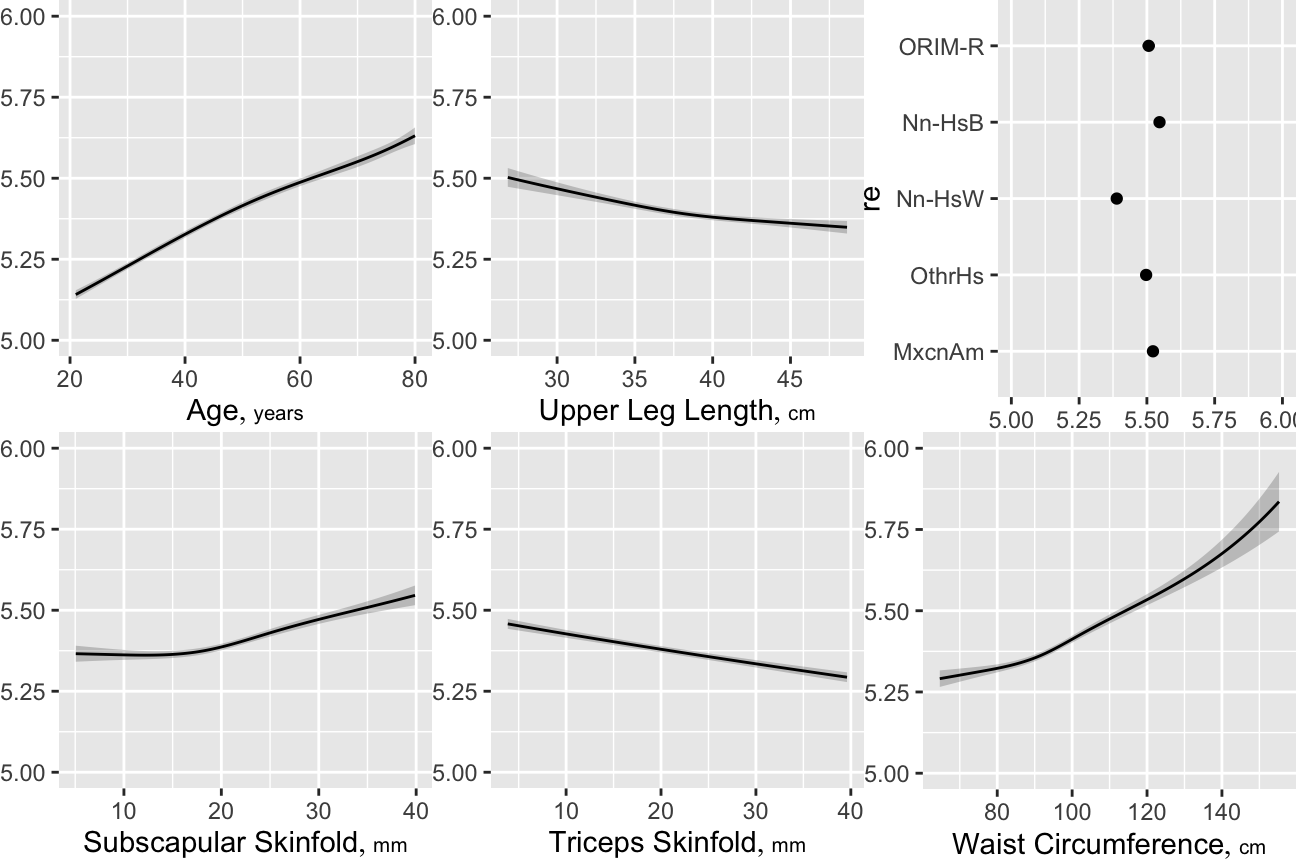
| ANOVA for reduced model after multiple imputation, with addition of a combined effect for four size variables | |||
| χ2 | d.f. | P | |
|---|---|---|---|
| age | 630.21 | 4 | <0.0001 |
| Nonlinear | 28.12 | 3 | <0.0001 |
| re | 172.14 | 4 | <0.0001 |
| leg | 24.25 | 2 | <0.0001 |
| Nonlinear | 1.64 | 1 | 0.2009 |
| waist | 152.89 | 3 | <0.0001 |
| Nonlinear | 3.87 | 2 | 0.1442 |
| tri | 33.22 | 1 | <0.0001 |
| sub | 36.85 | 3 | <0.0001 |
| Nonlinear | 5.28 | 2 | 0.0714 |
| TOTAL NONLINEAR | 42.48 | 8 | <0.0001 |
| TOTAL | 1336.94 | 17 | <0.0001 |
Compare the estimated age partial effects and confidence intervals with those from a model using casewise deletion, and with bootstrap nonparametric confidence intervals (also with casewise deletion).
pgc <- Predict(gc, age)
bootclb <- Predict(gb, age, boot.type='basic')
bootclp <- Predict(gb, age, boot.type='percentile')
multimp <- Predict(g, age)
p <- rbind('casewise deletion' = pgc,
'basic bootstrap' = bootclb,
'percentile bootstrap' = bootclp,
'multiple imputation' = multimp)[, .q(age, yhat, lower, upper, .set.)]
m <- melt(as.data.table(p), id.vars=c('age', '.set.'))
ggplot(m, aes(x=age, y=value, color=.set.,
group=paste(variable, .set.))) + geom_line() +
guides(color=guide_legend(title='')) +
theme(legend.position='bottom') +
ylab(expression(X * hat(beta)))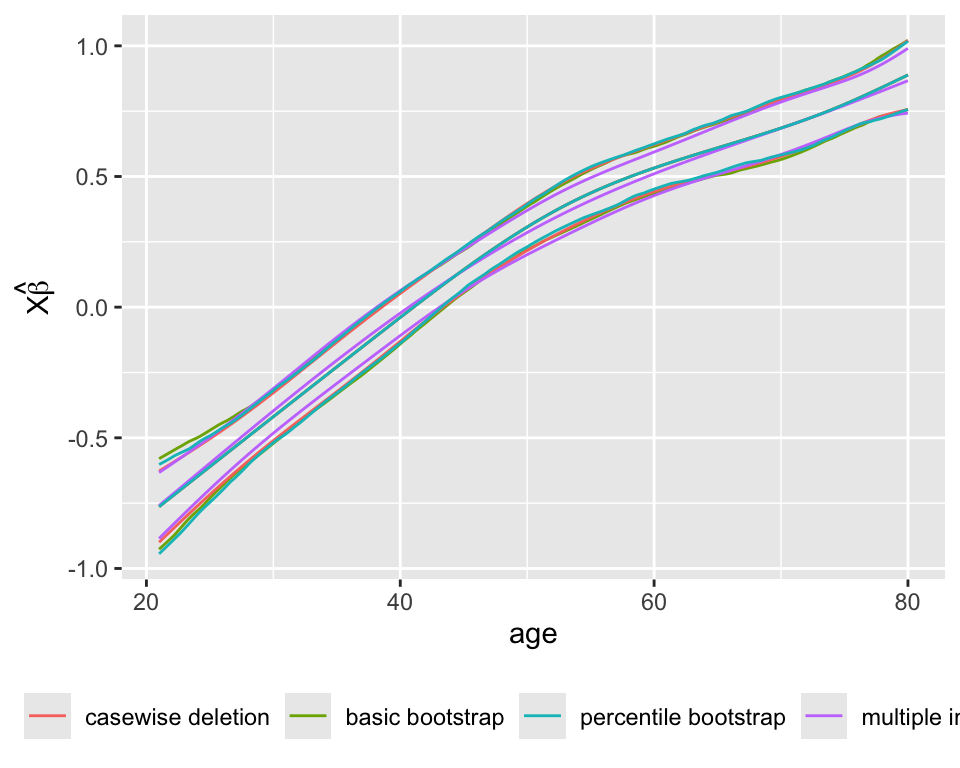
In OLS the mean equals the median and both are linearly related to any other quantiles. Semiparametric models are not this restrictive:
M <- Mean(g)
qu <- Quantile(g)
med <- function(lp) qu(.5, lp)
q90 <- function(lp) qu(.9, lp)
lp <- predict(g)
lpr <- quantile(predict(g), c(.002, .998), na.rm=TRUE)
lps <- seq(lpr[1], lpr[2], length=200)
pmn <- M(lps)
pme <- med(lps)
p90 <- q90(lps)
plot(pmn, pme,
xlab=expression(paste('Predicted Mean ', HbA["1c"])),
ylab='Median and 0.9 Quantile', type='l',
xlim=c(4.75, 8.0), ylim=c(4.75, 8.0), bty='n')
box(col=gray(.8))
lines(pmn, p90, col='blue')
abline(a=0, b=1, col=gray(.8))
text(6.5, 5.5, 'Median')
text(5.5, 6.3, '0.9', col='blue')
nint <- 350
scat1d(M(lp), nint=nint)
scat1d(med(lp), side=2, nint=nint)
scat1d(q90(lp), side=4, col='blue', nint=nint)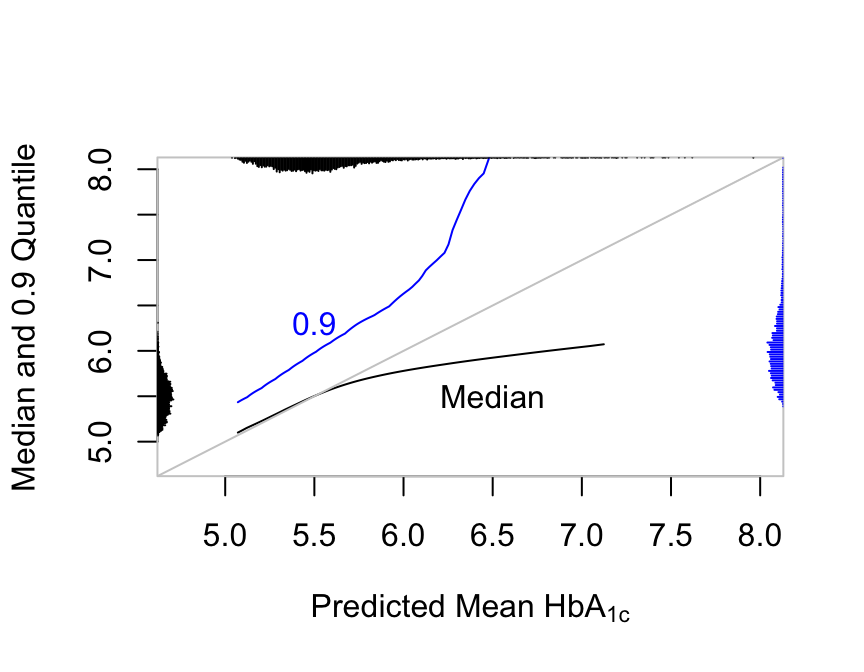
r hba vs. predicted median and 0.9 quantile along with their marginal distributions
Draw a nomogram to compute 7 different predicted values for each subject.
spar(ps=9)
g <- Newlevels(g, list(re=abbreviate(levels(w$re))))
exprob <- ExProb(g)
nom <-
nomogram(g, fun=list(Mean=M,
'Median Glycohemoglobin' = med,
'0.9 Quantile' = q90,
'Prob(HbA1c >= 6.5)'=
function(x) exprob(x, y=6.5),
'Prob(HbA1c >= 7.0)'=
function(x) exprob(x, y=7),
'Prob(HbA1c >= 7.5)'=
function(x) exprob(x, y=7.5)),
fun.at=list(seq(5, 8, by=.5),
c(5,5.25,5.5,5.75,6,6.25),
c(5.5,6,6.5,7,8,10,12,14),
c(.01,.05,.1,.2,.3,.4),
c(.01,.05,.1,.2,.3,.4),
c(.01,.05,.1,.2,.3,.4)))
plot(nom, lmgp=.28) 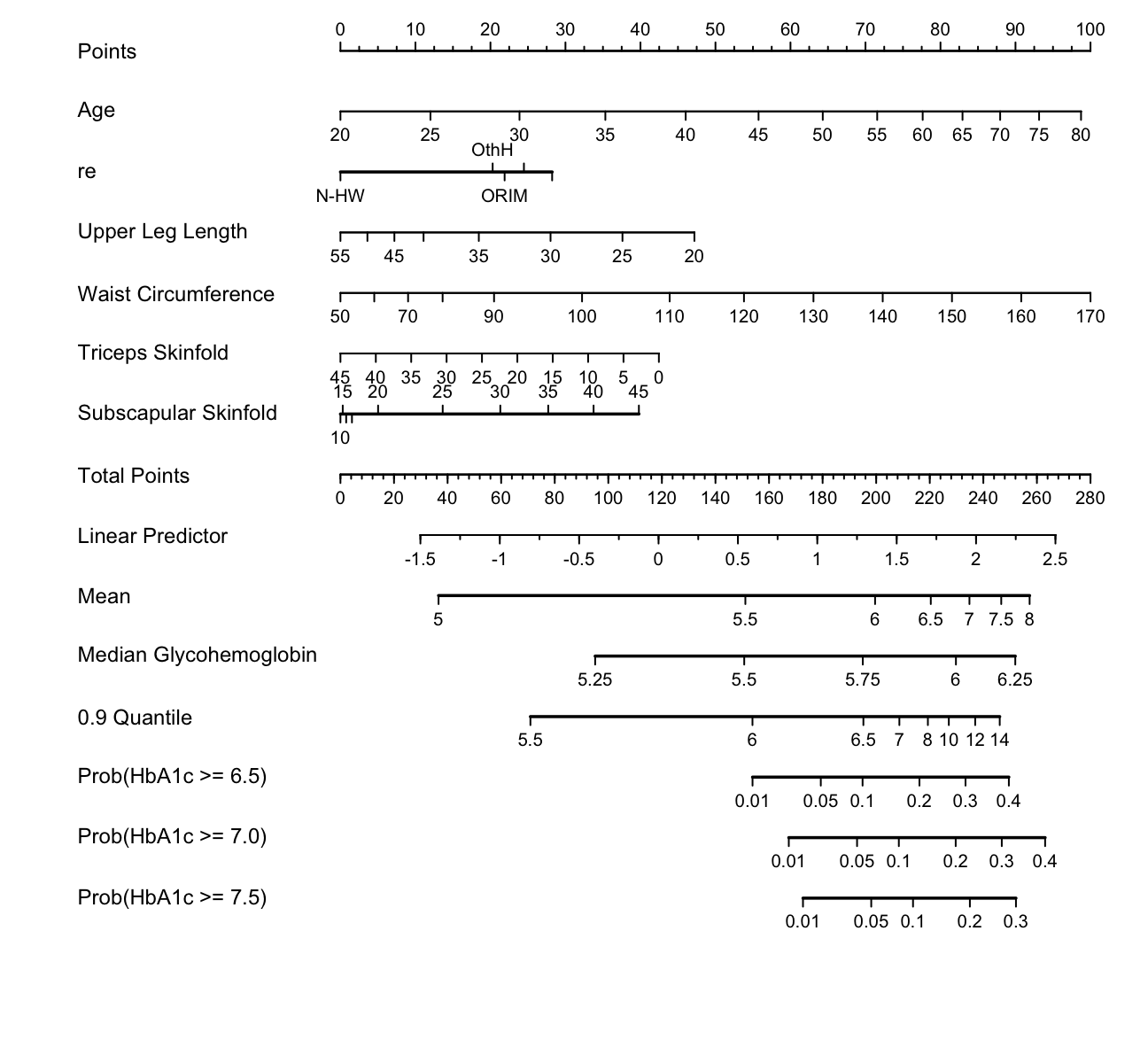
```{r include=FALSE}
require(Hmisc)
options(qproject='rms', prType='html')
require(qreport)
getRs('qbookfun.r')
hookaddcap()
knitr::set_alias(w = 'fig.width', h = 'fig.height', cap = 'fig.cap', scap ='fig.scap')
```
`r hba <- '$\\text{HbA}_{1c}$'`
# Regression Models for Continuous $Y$ and Case Study in Ordinal Regression {#sec-cony}
`r mrg(sound("ord-cont-1"))`
This chapter concerns univariate continuous $Y$. There are many
multivariable models for predicting such response variables.
`r ipacue()`
* linear models with assumed normal residuals, fitted with ordinary least squares
* generalized linear models and other parametric models based on
special distributions such as the gamma
* generalized additive models (GAMs)
* generalization of GAMs to also nonparametrically transform $Y$
* quantile regression (see Section @sec-cony-quantile-regression)
* other robust regression models that, like quantile regression, use
an objective different from minimizing the sum of squared errors [@VR]
* semiparametric models based on the ranks of $Y$, such as the Cox
proportional hazards model
and the proportional odds ordinal logistic model
* cumulative probability models (often called _cumulative link models_ despite the fact that cumulative probabilities and not cumulative links are being computed) which are semiparametric models from a wider class of families than the logistic
Semiparametric models that treat $Y$ as ordinal but not `r ipacue()`
interval-scaled have many advantages including robustness and freedom
of distributional assumptions for $Y$ conditional on any given set of
predictors.
<!-- Semiparametric models assume only a connection between--->
<!-- the distribution of $Y | X_{1}$ and $Y | X_{2}$.--->
Advantages are demonstrated in a case study of a cumulative
probability ordinal model. Some of the results are compared to quantile
regression and OLS. Many of the methods used in the case study also apply to
ordinary linear models.
## Dataset and Descriptive Statistics
`r mrg(sound("ord-cont-2"))`
* Diabetes Mellitus (DM) type II (adult onset diabetes) is strongly `r ipacue()`
associated with obesity
* Primary laboratory test for diabetes: glycosylated hemoglobin
(`r hba`), also called glycated hemoglobin, glycohemoglobin, or
hemoglobin $A_{1c}$.
* `r hba` reflects average blood glucose for the preceding 60 to 90 days
* `r hba` $> 7.0$ usually taken as a positive diagnosis of diabetes
* Goal of analysis:
+ better understand effects of body size measurements on risk of DM
+ enhance screening for DM
* Best way to develop a model for DM screening is **not** to `r ipacue()`
fit binary logistic model with `r hba` > 7 as the response variable
+ All cutpoints are arbitrary; no justification for any putative cut
+ `r hba` 2=6.9, 7.1=10
+ Larger standard errors of $\hat{\beta}$, lower power, wider
confidence bands
+ Better: predict continuous `r hba` using continuous response
model, then convert to probability `r hba` exceeds any cutoff or
estimate 0.9 quantile of `r hba`
* Data: U.S. National Health and Nutrition Examination Survey
(NHANES) `r ipacue()`
from National Center for Health Statistics/CDC:
[www.cdc.gov/nchs/nhanes.htm](http://www.cdc.gov/nchs/nhanes.htm) [@nhanes2010]
* age $\geq 80$ coded as 80 by CDC
* Subset with age $\geq 21$, neither diagnosed nor treated for DM
* Transform `bmi`, just for the spike histograms
```{r desc,results='asis'}
require(rms)
options(prType='html') # for print, summary, anova, describe
getHdata(nhgh)
w <- subset(nhgh, age >= 21 & dx==0 & tx==0, select=-c(dx,tx))
des <- describe(w, trans=list(bmi= list('log', log, exp)))
sparkline::sparkline(0) # loads jQuery javascript for sparklines
maketabs(print(des, 'both'), wide=TRUE, initblank=TRUE)
dd <- datadist(w); options(datadist='dd')
```
## The Linear Model {#sec-cony-linear-model}
`r mrg(sound("ord-cont-3"))`
The most popular multivariable model for analyzing a univariate
continuous $Y$ is the the linear model
$$
E(Y | X) = X \beta,
$$
where $\beta$ is estimated using ordinary least squares, that is, by
solving for $\hat{\beta}$ to minimize $\sum (Y_{i} - X \hat{\beta})^{2}$.
* To compute $P$-values and confidence limits using parametric `r ipacue()`
methods (and for least squares estimates to coincide with maximum
likelihood estimates)
we would have to assume that $Y | X$ is normal with mean $X \beta$ and
constant variance $\sigma^2$ ^[The latter assumption may be dispensed with if we use a robust Huber-White or bootstrap covariance matrix estimate. Normality may sometimes be dispensed with by using bootstrap confidence intervals, but this would not fix inefficiency problems with OLS when residuals are non-normal.]
<!-- * Don't assume linearity; expand $X$s into rcs with no. knots--->
<!-- figured by predictive potential; use default knit locations--->
<!-- (selected quantiles of continuous predictors' marginal distributions)--->
### Checking Assumptions of OLS and Other Models {#sec-cony-checkass}
* First see if `gh` would make a Gaussian residuals model fit `r ipacue()`
* Use ordinary regression on 4 key variables to collapse into one
variable (predicted mean from OLS model)
* Stratify predicted mean into 6 quantile groups
* Apply the normal inverse ECDF of `gh` to these strata
and check for normality and constant $\sigma^2$
* ECDF is for $\Pr[Y \leq y | X]$ but for ordinal modeling we
want to state models in terms of $\Pr[Y \ge y | X]$ so take 1 -
ECDF before inverse transforming
```{r lookdist,w=6.5,h=5.5,cap='Examination of normality and constant variance assumption, and assumptions for various ordinal models',scap='Examining normality and ordinal model assumptions'}
#| label: fig-cony-lookdist
f <- ols(gh ~ rcs(age,5) + sex + re + rcs(bmi, 3), data=w)
setDT(w) # make w a data.table
w[, pgh := fitted(f)]
w[, pgh6 := cut2(pgh, g=6)]
u <- w[, ecdfSteps(gh, extend=FALSE), by=pgh6] # ecdfSteps is in Hmisc
v <- rbind(data.table(trans='paste(Phi^-1, (F[n](x)))', u[, z := qnorm(1 - y) ]),
data.table(trans='logit(F[n](x))', u[, z := qlogis(1 - y) ]),
data.table(trans='-log(-log(F[n](x)))', u[, z := -log(-log(1 - y))]),
data.table(trans='log(-log(1-F[n](x)))', u[, z := log(-log(y)) ]))
v <- v[! is.infinite(z)]
ggplot(v, aes(x, z, color=pgh6)) + geom_step() +
facet_wrap(~ trans, label='label_parsed', scales='free_y') +
xlab(expression(HbA[`1c`])) + theme(legend.position='bottom')
# Get slopes of pgh for some cutoffs of Y
# Use glm complementary log-log link on Prob(Y < cutoff) to
# get log-log link on Prob(Y >= cutoff)
r <- NULL
for(link in c('logit','probit','cloglog'))
for(k in c(5, 5.5, 6)) {
co <- coef(glm(gh < k ~ pgh, data=w, family=binomial(link)))
r <- rbind(r, data.frame(link=link, cutoff=k,
slope=round(co[2],2)))
}
print(r, row.names=FALSE)
```
* Lower right curves are not linear, implying that a normal `r ipacue()`
conditional distribution cannot work for `gh`^[They are not parallel either.]
* There is non-parallelism for the logit model
* Other graphs will be used to guide selection of an ordinal model below
The `rms` `ordParallel` function makes it easy to vary coefficients over a continuum of cutoffs, and it has a algorithm for choosing cutpoints given a specify maximum number of cutoffs. As this allows different predictors to have different amounts of non-parallelism, this may be preferred to the 6-tiles approach.
```{r}
f <- orm(gh ~ rcs(age,5) + sex + re + rcs(bmi, 3), data=w, x=TRUE, y=TRUE)
ordParallel(f)
```
When there are multiple terms, it is difficult to interpret this plot. There is an option to combine all the terms for each predictor into a single partial linear predictor. Then y-varying effects are assessed with respect to this predictor summary measure. By default these partial linear predictors are scaled by their inter-quartile-range over observations so that weak predictors will not have exaggerated/irrelevant y-cutoff-dependencies.
```{r}
ordParallel(f, terms=TRUE)
```
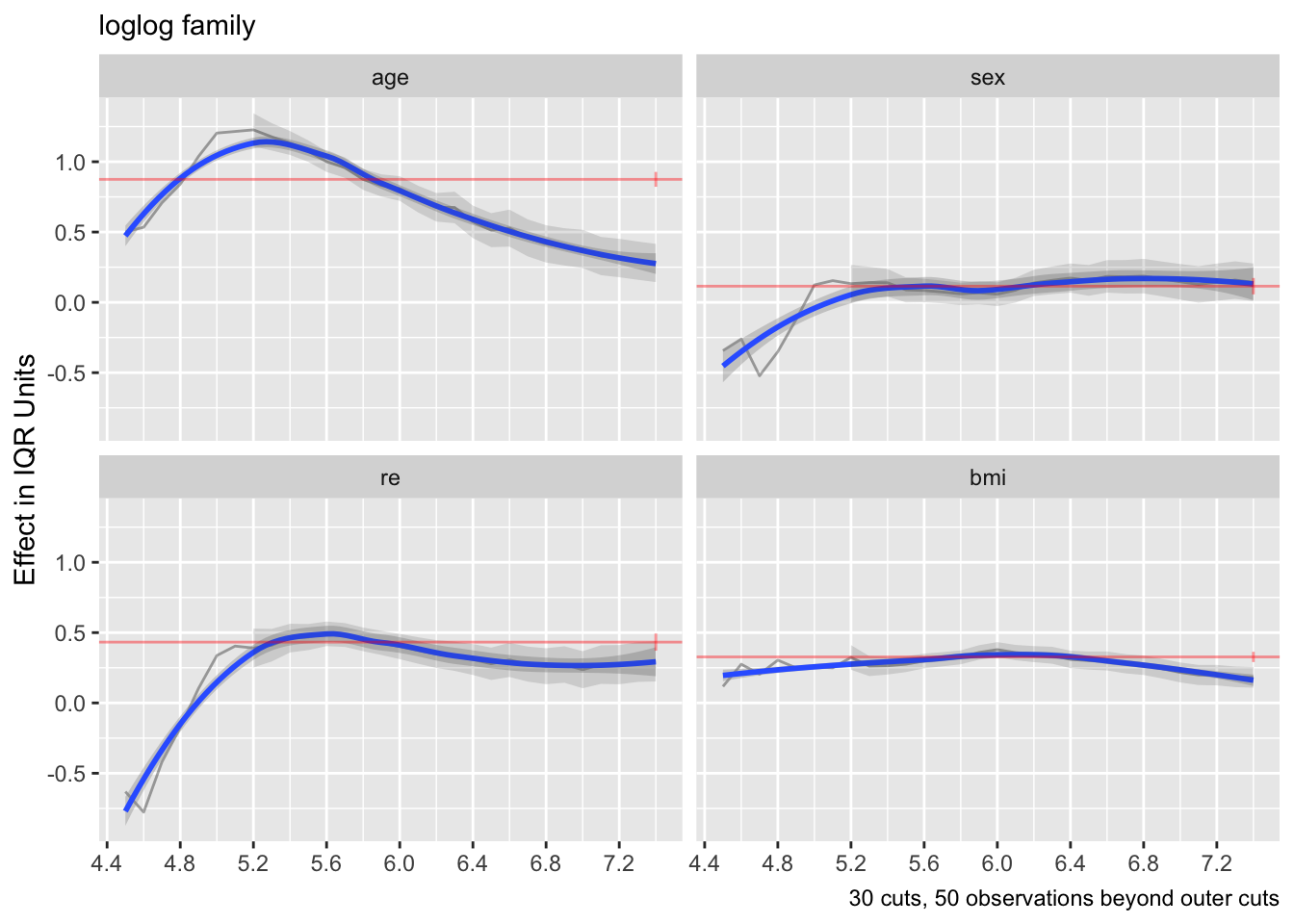
The above two plots were for the logit link. Re-run using the log-log link.
```{r}
f <- orm(gh ~ rcs(age,5) + sex + re + rcs(bmi, 3), family='loglog',
data=w, x=TRUE, y=TRUE)
ordParallel(f, terms=TRUE)
```
Effects appear to be more constant.
`ordParallel` has an `onlydata` option to make it produce a data frame instead of a graphic. The data frame is a stacked version of all the one-number "terms" summaries. The number of observations in the stacked data frame will be the number of cuts multiplied by the number of observations. A variable `obs` is included in the data frame so that one can see which original observation numbers correspond to each row of the stacked data. `obs` can be used as the `cluster` argument to `rms::robcov` to get robust cluster sandwich variance-covariance matrix estimates. These can be used to get wald tests for interactions between cutoffs and covariate, i.e., tests of parallelism. The following example shows how to do this for the two link functions.
```{r}
testpar <- function(form, link) {
f <- orm(form, data=w, family=link, x=TRUE, y=TRUE)
do <- ordParallel(f, onlydata=TRUE, maxcuts=30)
g <- orm(Yge_cut ~ (age + sex + bmi + re) * Ycut, data=do, x=TRUE, y=TRUE)
h <- robcov(g, do$obs)
print(anova(h))
invisible()
}
form <- gh ~ rcs(age,5) + sex + re + rcs(bmi, 3)
testpar(form, 'logistic') # Chunk test for global parallelism 151.17
testpar(form, 'loglog') # Chunk test 140.8
```
Another approach to goodness of fit is internal calibration plots. For a series of `gh` cutoffs plot the estimated actual probability of exceeding the cutoff as a function of the predicted probability of exceeding it.
```{r}
gcuts <- c(5.5, 6, 6.5, 7)
intCalibration(f, ycuts=gcuts) + labs(subtitle=f$family)
g <- update(f, family='logistic')
intCalibration(g, ycuts=gcuts) + labs(subtitle=g$family)
```
Using the adaptive linear spline HARE estimates, the logit link fits less well.
A different calibration plan is made by plotting both predicted and observed exceedance probabilities against a covariate.
```{r}
intCalibration(f, ycuts=gcuts, x=w$age) + labs(subtitle=f$famiy)
intCalibration(g, ycuts=gcuts, x=w$age) + labs(subtitle=g$famiy)
```
Finally, the `rms` `Olinks` function computes deviance measures for a series of link functions. Though this may not detect Y-dependency of effects (nonparallelism) with respect to a single predictor, it is useful for choosing the overall model. Model fits are automatically re-run by `Olinks` for a series of links not used in the current fit.
```{r}
Olinks(f)
```
Oddly, the logit link had the smallest deviance. More study of comparing deviances is needed.
## Quantile Regression {#sec-cony-quantile-regression}
`r mrg(sound("ord-cont-4"))`
* Ruled out OLS and semiparametric proportional odds model `r ipacue()`
* Quantile regression [@koeqr; @koe78reg] is a
different approach to modeling $Y$
* No distributional assumptions other than continuity of $Y$
* All the usual right hand side assumptions
* When there is a single
predictor that is categorical, quantile regression coincides with
ordinary sample quantiles stratified by that predictor
* Is transformation invariant - pre-transforming $Y$ not important
Let $\rho_{\tau}(y) = y(\tau - [y < 0])$. The $\tau^{\mathrm th}$
sample `r ipacue()`
quantile is the minimizer $q$ of
$\sum_{i-1}^{n}\rho_{\tau}(y_{i}-q)$. For a conditional
$\tau^{\mathrm th}$ quantile of $Y | X$ the corresponding quantile regression estimator
$\hat{\beta}_{\tau}$ minimizes $\sum_{i=1}^{n}\rho_{\tau}(Y_{i}-X\beta)$.
Quantile regression is not as efficient at
estimating quantiles as is ordinary least squares at estimating the
mean, if the latter's assumptions hold.
Koenker's `quantreg` package in `R` [@quantreg] implements
quantile regression, and the `rms` package's `Rq` function
provides a front-end that gives rise to various graphics and inference tools.
If we model the median `gh` as a function of covariates, only the
$X\beta$ structure need be correct. Other quantiles (e.g.,
$90^\text{th}$ percentile) can be directly modeled but standard errors will
be much larger as it is more difficult to precisely estimate outer quantiles.
## Ordinal Regression Models for Continuous $Y$
`r mrg(sound("ord-cont-5"))`
* Advantages of semiparametric models (e.g., quantile regression `r ipacue()`
and cumulative probability ordinal models
* For ordinal cumulative probability models, there is no
distributional assumption for $Y$ given a setting of $X$
* Assume only a connection between distributions of $Y$ for
different $X$
* Applying an increasing 1--1 transformation to $Y$ results in no change to
regression coefficient estimates^[For symmetric distributions applying a decreasing transformation will negate the coefficients. For asymmetric distributions (e.g., Gumbel), reversing the order of $Y$ will do more than change signs.]
* Regression coefficient estimates are completely robust to
extreme $Y$ values^[Only an estimate of mean $Y$ from these $\hat{\beta}$s is non-robust.]
* Estimates of quantiles of $Y$ are exactly
transformation-preserving, e.g., estimate of median of $\log Y$ is
exactly the log of the estimate of median $Y$
* @man10ord developed an ordinal model for
continuous $Y$ which they incorrectly labeled semi-parametric and is
actually a lower-dimensional flexible parametric model that instead
of having intercepts has a spline function of $y$.
----
For a general continuous distribution `r ipacue()` function $F(y)$, an ordinal
regression model based on cumulative probabilities may be stated as
follows^[It is more traditional to state the model in terms of $\Pr[Y \leq y | X]$ but we use $\Pr[Y \geq y | X]$ so that higher predicted values are associated with higher $Y$.]. Let the ordered
unique values of $Y$ be denoted by $y_{1}, y_{2}, \dots, y_{k}$ and
let the intercepts associated with $y_{1}, \dots, y_{k}$ be
$\alpha_{1}, \alpha_{2}, \dots, \alpha_{k}$, where $\alpha_{1} =
\infty$ because $\Pr[Y \geq y_{1}] = 1$. Let $\alpha_{y} =
\alpha_{i}, i:y_{i}=y$. Then
$$
\Pr[Y \geq y_{i} | X] = F(\alpha_{i} + X\beta) = F(\alpha_{y_{i}} + X\beta)
$$
For the OLS fully parametric case, the model may
be restated
\begin{array}{c}
\Pr[Y \geq y | X] = \Pr[\frac{Y-X\beta}{\sigma} \geq
\frac{y-X\beta}{\sigma}]\\ = 1-\Phi(\frac{y-X\beta}{\sigma}) = \Phi(\frac{-y}{\sigma}+\frac{X\beta}{\sigma})
\end{array}
so that to within an additive constant ^[$\hat{\alpha_{y}}$ are unchanged if a constant is added to all $y$.] $\alpha_{y} = \frac{-y}{\sigma}$ (intercepts $\alpha$ are
linear in $y$ whereas they are arbitrarily descending in the ordinal model), and
$\sigma$ is absorbed in $\beta$ to put the OLS model into the new notation.
The general ordinal regression model assumes that for fixed $X_{1}, X_{2}$,
\begin{array}{c}
F^{-1}(\Pr[Y \geq y | X_{2}]) - F^{-1}(\Pr[Y \geq y | X_{1}])\\
= (X_{2} - X_{1})\beta
\end{array}
independent of the $\alpha$s (parallelism assumption). If $F = [1 +
\exp(-y)]^{-1}$, this is the proportional odds assumption.
Common choices of $F$, implemented in the `rms` `orm` function,
are shown in Table @tbl-cony-ormdist. `r ipacue()`
| Distribution | $F$ | Inverse (Link Function) | Link Name | Connection |
|-----|-----|-----|-----|-----|
| Logistic | $[1 + \exp(-y)]^{-1}$ | $\log(\frac{y}{1-y})$ | logit | $\frac{P_{2}}{1-P_{2}} = \frac{P_{1}}{1-P_{1}} \exp(\Delta)$ |
| Gaussian | $\Phi(y)$ | $\Phi^{-1}(y)$ | probit | $P_{2}=\Phi(\Phi^{-1}(P_{1})+\Delta)$ |
| Gumbel maximum value| $\exp(-\exp(-y))$ | $\log(-\log(y))$ | $\log-\log$ | $P_{2}=P_{1}^{\exp(\Delta)}$ |
| Gumbel minimum value| $1 - \exp(-\exp(y))$ | $\log(-\log(1 - y))$ | complementary $\log-\log$ | $1-P_{2}=(1-P_{1})^{\exp(\Delta)}$ |
| Cauchy | $\frac{1}{\pi}\tan^{-1}(y) + \frac{1}{2}$ | $\tan[\pi(y - \frac{1}{2})]$ | cauchit |
: Distribution families used in ordinal cumulative probability models. $\Phi$ denotes the Gaussian cumulative distribution function. For the Connection column, $P_{1}=\Pr[Y \geq y | X_{1}], P_{2}=\Pr[Y \geq y | X_{2}], \Delta=(X_{2}-X_{1})\beta$. The connection specifies the only distributional assumption if the model is fitted semiparametrically, i.e, contains an intercept for every unique $Y$ value less one. For parametric models, $P_{1}$ must be specified absolutely instead of just requiring a relationship between $P_{1}$ and $P_{2}$. For example, the traditional Gaussian parametric model specifies that $\Pr[Y \geq y | X] = 1 - \Phi(\frac{y - X\beta}{\sigma}) = \Phi(\frac{-y + X\beta}{\sigma})$. {#tbl-cony-ormdist}
The Gumbel maximum value distribution is also called the extreme value
type I distribution. This distribution
($\log-\log$ link) also represents a continuous time proportional
hazards model. The hazard
ratio when $X$ changes from $X_{1}$ to $X_{2}$ is $\exp(-(X_{2} -
X_{1}) \beta)$.
The mean of $Y | X$ is easily estimated by computing `r ipacue()`
$$
\sum_{i=1}^{k} y_{i} \hat{\Pr}[Y = y_{i} | X]
$$
and the $q^\text{th}$ quantile of $Y | X$ is $y$ such that <br>
$F^{-1}(1 - q) - X\hat{\beta} = \hat{\alpha}_{y}$.^[The intercepts have to be shifted to the left one position in solving this equation because the quantile is such that $\Pr[Y \leq y] = q$ whereas the model is stated in terms of $\Pr[Y \geq y]$.]
The `orm` function in the `rms` package takes advantage of the
information matrix being of a sparse tri-band diagonal form for the
intercept parameters. This makes the computations efficient even for
hundreds of intercepts (i.e., unique values of $Y$). `orm` is made
to handle continuous $Y$.
Ordinal regression has nice properties in addition to those listed
above, allowing for
* estimation of quantiles as efficiently as quantile `r ipacue()`
regression if the parallel slopes assumptions hold
* efficient estimation of mean $Y$
* direct estimation of $\Pr[Y\geq y | X]$
* arbitrary clumping of values of $Y$, while still
estimating $\beta$ and mean $Y$ efficiently^[But it is not sensible to estimate quantiles of $Y$ when there are heavy ties in $Y$ in the area containing the quantile.]
* solutions for $\hat{\beta}$ using ordinary Newton-Raphson or
other popular optimization techniques
* being based on a standard likelihood function, penalized
estimation can be straightforward
* Wald, score, and likelihood ratio $\chi^2$ tests that are more
powerful than tests from quantile regression
To summarize how assumptions of parametric models `r ipacue()` compare to
assumptions of semiparametric models, consider the ordinary linear
model or its special case the equal variance
two-sample $t$-test, vs. the probit or logit (proportional odds)
ordinal model or their special cases the Van der Waerden
(normal-scores) two-sample test or the Wilcoxon test. All the
assumptions of the linear model other than independence of residuals
are captured in the following (written in traditional $Y\leq y$ form):
\begin{array}{c}
F(y|X) = \Pr[Y \leq y|X] = \Phi(\frac{y-X\beta}{\sigma})\\
\Phi^{-1}(F(y|X)) = \frac{y-X\beta}{\sigma}
\end{array}
```{r lmassump,h=3.5,w=8,left=2,cap='Assumptions of the linear model (left panel) and semiparametric ordinal probit or logit (proportional odds) models (right panel). Ordinal models do not assume any shape for the distribution of $Y$ for a given $X$; they only assume parallelism.',scap='Assumptions of linear vs. semiparametric models'}
#| label: fig-cony-lmassump
spar(mfrow=c(1,2), left=2)
pinv <- expression(paste(Phi^{-1}, '(F(y', '|', 'X))'))
plot(0, 0, xlim=c(0, 1), ylim=c(-2, 2), type='n', axes=FALSE,
xlab=expression(y), ylab='')
mtext(pinv, side=2, line=1)
axis(1, labels=FALSE, lwd.ticks=0)
axis(2, labels=FALSE, lwd.ticks=0)
abline(a=-1.5, b=1)
abline(a=0, b=1)
arrows(.5, -1.5+.5, .5, 0+.5, code=3, length=.1)
text(.525, .5*(-1.5+.5+.5), expression(-Delta*X*beta/sigma), adj=0)
g <- function(x) -2.2606955+11.125231*x-37.772783*x^2+56.776436*x^3-
26.861103*x^4
x <- seq(0, .9, length=150)
pinv <- expression(atop(paste(Phi^{-1}, '(F(y', '|', 'X))'),
paste(logit, '(F(y', '|', 'X))')))
plot(0, 0, xlim=c(0, 1), ylim=c(-2, 2), type='n', axes=FALSE,
xlab=expression(y), ylab='')
mtext(pinv, side=2, line=1)
axis(1, labels=FALSE, lwd.ticks=FALSE)
axis(2, labels=FALSE, lwd.ticks=FALSE)
lines(x, g(x))
lines(x, g(x)+1.5)
arrows(.5, g(.5), .5, g(.5)+1.5, code=3, length=.1)
text(.525, .5*(g(.55) + g(.55)+1.5), expression(-Delta*X*beta), adj=0)
```
On the other hand, ordinal models assume the following:
$$
\Pr[Y \leq y|X] = F(g(y)-X\beta),
$$
where $g$ is unknown and may be discontinuous.
From this point we revert back to $Y\geq y$ notation so that $Y$
increases as $X\beta$ increases.
**Global Modeling Implications**
* Ordinal regression invariant to choice of transformation of $Y$ `r ipacue()`
* $Y$ needs to be ordinal
* Difference in two ordinal variables is not necessarily ordinal
* $\rightarrow$ Never analyze differences in regression
* $Y$=final value, adjust for baseline values as covariates
## Ordinal Regression Applied to `r hba`
`r mrg(sound("ord-cont-6"))`
* In @fig-cony-lookdist, logit inverse curves are not `r ipacue()`
parallel so proportional odds assumption does not hold
* log-log link yields highest degree of parallelism and most
constant regression coefficients across cutoffs of `gh` so use this
link in an ordinal regression model (linearity of the curves is not required)
### Checking Fit for Various Models Using Age
`r ipacue()`
Another way to examine model fit is to flexibly fit the single most
important predictor (age) using a variety of methods, and comparing
predictions to sample quantiles and means based on overlapping subsets
on age, each subset being subjects having age $< 5$ years away from
the point being predicted by the models. Here we predict the 0.5,
0.75, and 0.9 quantiles and the mean. For quantiles we can compare to
quantile regression(discussed below) and for means we compare to OLS.
```{r comparemany,h=6.5,w=6.75,cap='Three estimated quantiles and estimated mean using 6 methods, compared against caliper-matched sample quantiles/means (circles). Numbers are mean absolute differences between predicted and sample quantities using overlapping intervals of age and caliper matching. QR:quantile regression.',scap='Six methods for estimating quantiles or means.'}
#| label: fig-cony-comparemany
require(data.table)
require(ggplot2)
estimands <- .q(q2, q3, p90, mean)
links <- .q(logistic, probit, loglog, cloglog)
estimators <- c(.q(empirical, ols, QR), links)
ages <- 25 : 75
nage <- length(ages)
yhat <- numeric(length(ages))
fmt <- function(x) format(round(x, 3), nsmall=3)
r <- expand.grid(estimand=estimands, estimator=estimators, age=ages,
y=NA_real_, stringsAsFactors=FALSE)
setDT(r)
# Discard irrelevant methods for estimands
r <- r[! (estimand == 'mean' & estimator == 'QR') &
! (estimand %in% .q(q2, q3, p90) & estimator == 'ols'), ]
# Find all used combinations
rc <- r[age == 25]
rc[, age := NULL]
mod <- gh ~ rcs(age,6)
# Compute estimates for all relevant combinations of estimands & estimators
for(eor in rc[, unique(estimator)]) {
if(eor == 'empirical') {
emp <- matrix(NA, nrow=nage, ncol=4,
dimnames=list(NULL, .q(mean, q2, q3, p90)))
for(j in 1 : length(ages)) {
s <- which(abs(w$age - ages[j]) < 5)
y <- w$gh[s]
a <- quantile(y, probs=c(0.5, 0.75, 0.90))
emp[j, ] <- c(mean(y), a)
}
}
else if(eor == 'ols') fit <- ols(mod, data=w)
else if(eor %in% links) fit <- orm(mod, data=w, family=eor)
for(eand in rc[estimator == eor, unique(estimand)]) {
qa <- switch(eand, q2=0.5, q3=0.75, p90=0.90)
yhat <- if(eor == 'ols') Predict(fit, age=ages, conf.int=FALSE)$yhat
else if(eor == 'empirical') emp[, eand]
else if(eor == 'QR') {
fit <- Rq(mod, data=w, tau=qa)
Predict(fit, age=ages, conf.int=FALSE)$yhat
}
else {
fun <- switch(eand,
mean = Mean(fit),
Quantile(fit))
fu <- if(eand == 'mean') fun
else function(x) fun(qa, x)
Predict(fit, age=ages, fun=fu, conf.int=FALSE)$yhat
}
r[estimand == eand & estimator == eor, y := yhat]
}
}
# Compute age-specific differences between estimates and empirical
# estimates, then compute mean absolute differences across all ages
dif <- r[estimator != 'empirical']
for(eor in rc[, setdiff(unique(estimator), 'empirical')])
for(eand in rc[estimator == eor, unique(estimand)])
dif[estimator == eor & estimand == eand]$y <-
r[estimator == eor & estimand == eand]$y -
r[estimator == 'empirical' & estimand == eand]$y
mad <- dif[, .(ad = mean(abs(y))), by=.(estimand, estimator)]
mad2 <- mad[, .(value = paste(fmt(ad), collapse='\n'),
label = paste(estimator, collapse='\n'),
x = if(estimand == 'p90') 60 else 25,
y = if(estimand == 'p90') 5.5 else 6.2),
by=.(estimand)]
ggplot() + geom_line(aes(x=age, y=y, col=estimator),
data=r[estimator != 'empirical']) +
geom_point(aes(x=age, y=y, alpha=I(0.35)),
data=r[estimator == 'empirical']) +
facet_wrap(~ estimand) +
geom_text(aes(x=x, y=y, label=label, hjust='left', size=I(3)), data=mad2) +
geom_text(aes(x=x+10, y=y, label=value, hjust='left', size=I(3)), data=mad2) +
guides(color=guide_legend(title='')) +
theme(legend.position='bottom')
```
`r ipacue()`
It can be seen in @fig-cony-comparemany that models
dedicated to a specific task (quantile regression for quantiles and
OLS for means) were best for those tasks.
Although the log-log ordinal cumulative probability model did not
estimate the median as accurately as some other methods, it does well
for the 0.75 and 0.9 quantiles and is the best compromise overall because
of its ability to also directly predict the mean as well as quantities
such as $\Pr[\text{HbA}_{1c} > 7 | X]$.
For here on we focus on the log-log ordinal model.
Going back to the bottom left of `r ipacue()`
@fig-cony-lookdist, let's look at quantile groups
of predicted `r hba` by OLS and plot predicted distributions of actual
`r hba` against empirical distributions.
```{r predobs,w=5.5,h=5,cap='Observed (dashed lines, open circles) and predicted (solid lines, closed circles) exceedance probability distributions from a model using 6-tiles of OLS-predicted $\\text{HbA}_{1c}$. Key shows quantile group intervals of predicted mean $\\text{HbA}_{1c}$.',scap='Observed and predicted distributions'}
#| label: fig-cony-predobs
###w$pghg <- cut2(pgh, g=6)
f <- orm(gh ~ pgh6, family='loglog', data=w)
lp <- predict(f, newdata=data.frame(pgh6=levels(w$pgh6)))
ep <- ExProb(f) # Exceedance prob. functn. generator in rms
z <- ep(lp)
j <- order(w$pgh6) # puts in order of lp (levels of pghg)
plot(z, xlim=c(4, 7.5), data=w[j,c('pgh6', 'gh')])
```
Agreement between predicted and observed exceedance probability
distributions is excellent in @fig-cony-predobs.
To return to the `r ipacue()` initial look at a linear model with assumed Gaussian
residuals, fit a probit ordinal model and compare the estimated
intercepts to the linear relationship with `gh` that is assumed by
the normal distribution.
```{r lookprobit,cap='Estimated intercepts from probit model'}
#| label: fig-cony-lookprobit
#| fig-height: 2.75
#| fig-width: 3.5
spar(bty='l')
f <- orm(gh ~ rcs(age,6), family='probit', data=w)
g <- ols(gh ~ rcs(age,6), data=w)
s <- g$stats['Sigma']
yu <- f$yunique[-1]
r <- quantile(w$gh, c(.005, .995))
alphas <- coef(f)[1:num.intercepts(f)]
plot(-yu / s, alphas, type='l', xlim=rev(- r / s),
xlab=expression(-y/hat(sigma)), ylab=expression(alpha[y]))
```
@fig-cony-lookprobit depicts a significant
departure from that implied by Gaussian residuals.
### Examination of BMI
`r mrg(sound("ord-cont-7"))`
Using the log-log model, we first check the adequacy of BMI as a
summary of height and weight for estimating median `gh`.
* Adjust for age (without assuming linearity) in every case `r ipacue()`
* Look at ratio of coefficients of log height and log weight
* Use AIC to judge whether BMI is an adequate summary of height
and weight
```{r htwtcoef}
f <- orm(gh ~ rcs(age,5) + log(ht) + log(wt),
family='loglog', data=w)
f
```
```{r aichtwt}
aic <- NULL
for(mod in list(gh ~ rcs(age,5) + rcs(log(bmi),5),
gh ~ rcs(age,5) + rcs(log(ht),5) + rcs(log(wt),5),
gh ~ rcs(age,5) + rcs(log(ht),4) * rcs(log(wt),4)))
aic <- c(aic, AIC(orm(mod, family='loglog', data=w)))
print(aic)
```
The ratio of the coefficient of log height `r ipacue()` to the coefficient of log
weight is `r round(coef(f)['ht']/coef(f)['wt'],1)`, which is
between what BMI uses and the more dimensionally reasonable
weight / height$^{3}$. By AIC, a spline interaction
surface between height and weight does slightly better than BMI in
predicting `r hba`, but a nonlinear function of BMI is barely worse. It
will require other body size measures to displace BMI as a predictor.
As an aside, compare this model fit to that from the Cox proportional
hazards model.
The Cox model uses a conditioning argument to obtain a partial
likelihood free of the intercepts $\alpha$ (and requires a second
step to estimate these log discrete hazard components) whereas we are
using a full marginal likelihood of the ranks of $Y$ [@kal73].
```{r coxhtwtcoef}
cph(Surv(gh) ~ rcs(age,5) + log(ht) + log(wt), data=w)
```
Back up and look at all body size measures, and examine their
redundancies. `r ipacue()`
```{r redun,h=6,w=6,cap='Variable clustering for all potential predictors'}
#| label: fig-cony-redun
v <- varclus(~ wt + ht + bmi + leg + arml + armc + waist +
tri + sub + age + sex + re, data=w)
plot(v)
# Omit wt so it won't be removed before bmi
r <- redun(~ ht + bmi + leg + arml + armc + waist + tri + sub,
data=w, r2=.75)
r
r2describe(r$scores, nvmax=5) # show strongest predictors of each variable
```
Six size measures adequately capture the entire set. Height and BMI
are removed.
An advantage of removing height `r ipacue()` is that it is age-dependent in
the elderly:
```{r htchange,cap="Estimated median height as a smooth function of age, allowing age to interact with sex, from a proportional odds model",scap="Median height vs. age"}
#| label: fig-cony-htchange
f <- orm(ht ~ rcs(age,4)*sex, data=w) # Prop. odds model
qu <- Quantile(f); med <- function(x) qu(.5, x)
ggplot(Predict(f, age, sex, fun=med, conf.int=FALSE),
ylab='Predicted Median Height, cm')
```
**But** also see a change in leg length:
```{r legchange,cap="Estimated median upper leg length as a smooth function of age, allowing age to interact with sex, from a proportional odds model",scap="Median leg length vs. age"}
#| label: fig-cony-legchange
f <- orm(leg ~ rcs(age,4)*sex, data=w)
qu <- Quantile(f); med <- function(x) qu(.5, x)
ggplot(Predict(f, age, sex, fun=med, conf.int=FALSE),
ylab='Predicted Median Upper Leg Length, cm')
```
Next allocate d.f. according to generalized Spearman `r ipacue()`
`r mrg(sound("ord-cont-8"))`
$\rho^{2}$ ^[Competition between collinear size measures hurts interpretation of partial tests of association in a saturated additive model.].
```{r allocadf,h=3, w=4,cap='Generalized squared rank correlations'}
#| label: fig-cony-allocadf
spar(top=1, ps=9)
s <- spearman2(gh ~ age + sex + re + wt + leg + arml + armc +
waist + tri + sub, data=w, p=2)
plot(s)
```
Parameters will be allocated in descending order of $\rho^2$. But
note that subscapular skinfold has a large number of `NA`s and
other predictors also have `NA`s. Suboptimal casewise deletion
will be used until the final model is fitted.
Because there are many competing `r ipacue()` body measures, we use backwards
stepdown to arrive at a set of predictors. The bootstrap will be used
to penalize predictive ability for variable selection. First the full
model is fit using
casewise deletion, then we do a composite test to assess whether any
of the frequently-missing predictors is important. Use likelihood ratio $\chi^2$ tests.
```{r fitfullcasewise}
f <- orm(gh ~ rcs(age,5) + sex + re + rcs(wt,3) + rcs(leg,3) + arml +
rcs(armc,3) + rcs(waist,4) + tri + rcs(sub,3),
family='loglog', data=w, x=TRUE, y=TRUE)
print(f, coefs=FALSE)
## Composite test:
anova(f, leg, arml, armc, waist, tri, sub, test='LR')
```
<!-- s <- f$stats--->
<!-- cat(sprintf('{<br>tszs$n=%g, p=%g, g=%g, <br>rho=%g$}',--->
<!-- s['Obs'], s['d.f.'], round(s['g'],3),--->
<!-- round(s['rho'], 3)), '\n')--->
The model yields Spearman $\rho=`r round(f$stats['rho'],3)`$, the
rank correlation between predicted and observed `r hba`.
Show predicted mean and median `r hba` `r ipacue()` as a function of age, adjusting
other variables to median/mode. Compare the estimate of the median
with that from quantile regression (discussed below).
```{r casewisemeanmed,h=4,w=5,cap='Estimated mean and 0.5 and 0.9 quantiles from the log-log ordinal model using casewise deletion, along with predictions of 0.5 and 0.9 quantiles from quantile regression (QR). Age is varied and other predictors are held constant to medians/modes.',scap='Estimated mean and quantiles from casewise deletion model.'}
#| label: fig-cony-casewisemeanmed
M <- Mean(f)
qu <- Quantile(f)
med <- function(x) qu(.5, x)
p90 <- function(x) qu(.9, x)
fq <- Rq(formula(f), data=w)
fq90 <- Rq(formula(f), data=w, tau=.9)
pmean <- Predict(f, age, fun=M, conf.int=FALSE)
pmed <- Predict(f, age, fun=med, conf.int=FALSE)
p90 <- Predict(f, age, fun=p90, conf.int=FALSE)
pmedqr <- Predict(fq, age, conf.int=FALSE)
p90qr <- Predict(fq90, age, conf.int=FALSE)
z <- rbind('orm mean'=pmean, 'orm median'=pmed, 'orm P90'=p90,
'QR median'=pmedqr, 'QR P90'=p90qr)
ggplot(z, groups='.set.',
adj.subtitle=FALSE, legend.label=FALSE)
```
Next do fast backward step-down `r ipacue()` in an attempt to get a model without so much competition among variables. The stepwise selection will be penalized for in the model validation.
`r mrg(sound("ord-cont-9"))`
```{r prbw}
print(fastbw(f, rule='p'), estimates=FALSE)
```
Validate the model, `r ipacue()` properly penalizing for variable selection
```{r valbworm}
g <- function() {
set.seed(13) # so can reproduce results
validate(f, B=100, bw=TRUE, estimates=FALSE, rule='p')
}
v <- runifChanged(g)
```
```{r prval}
# Show number of variables selected in first 30 boots
print(v, B=30)
```
Develop multiple imputations then repeat the bootstrap validation process, but separately for each completed dataset. The overall validation averages the bootstrap-corrected model performance measures over five validations.
```{r aregi}
set.seed(11)
a <- aregImpute(~ gh + age + sex + re + wt + leg + arml + armc + waist +
tri + sub, data=w, n.impute=5, pr=FALSE)
a
v <- function(fit)
list(validate=validate(fit, B=100, bw=TRUE, estimates=FALSE,
prmodsel=FALSE, rule='p', pr=FALSE))
h <- function()
fit.mult.impute(gh ~ rcs(age,5) + sex + re + rcs(wt,3) + rcs(leg,3) + arml +
rcs(armc,3) + rcs(waist,4) + tri + rcs(sub,3),
orm, a, data=w,
fun=v, fitargs=list(x=TRUE, y=TRUE, family='loglog'), pr=FALSE)
f <- runifChanged(h, a, v) # 11m
print(processMI(f, 'validate'), B=10, digits=3)
```
There is no `calibrate` method for `orm` model fits.
Next fit the reduced model. Use multiple imputation to impute missing
`r ipacue()` predictors.
Do a LR ANOVA for the reduced model, `r ipacue()` taking imputation into account.
```{r sanova}
h <- function()
fit.mult.impute(gh ~ rcs(age,5) + re + rcs(leg,3) +
rcs(waist,4) + tri + rcs(sub,4),
orm, a, fitargs=list(family='loglog'),
lrt=TRUE,
data=w, pr=FALSE)
g <- runifChanged(h, a)
g
an <- processMI(g, 'anova')
# Show penalty-type parameters for imputation
prmiInfo(an)
# Correct likelihood-based statistics for imputation
g <- LRupdate(g, an)
print(an, caption='ANOVA for reduced model after multiple imputation, with addition of a combined effect for four size variables')
b <- anova(g, leg, waist, tri, sub)
# Add new lines to the plot with combined effect of 4 size var.
s <- rbind(an, size=b['TOTAL', ])
class(s) <- 'anova.rms'
```
```{r sanovaplot,cap="ANOVA for reduced model after multiple imputation"}
#| label: fig-cony-sanova
#| fig-height: 3
spar(top=1)
plot(s)
```
`r ipacue()`
`r mrg(sound("ord-cont-10"))`
```{r peffects,cap='Partial effects (log hazard or log-log cumulative probability scale) of all predictors in reduced model, after multiple imputation',scap='Partial effects after multiple imputation',w=6.75,h=4.5}
#| label: fig-cony-peffects
ggplot(Predict(g), abbrev=TRUE, ylab=NULL)
```
`r ipacue()`
```{r mpeffects,cap='Partial effects (mean scale) of all predictors in reduced model, after multiple imputation',scap='Partial effects (means) after multiple imputation',w=6.75,h=4.5}
#| label: fig-cony-mpeffects
M <- Mean(g)
ggplot(Predict(g, fun=M), abbrev=TRUE, ylab=NULL)
```
Compare the estimated age `r ipacue()` partial effects and confidence intervals
with
those from a model using casewise deletion, and with bootstrap
nonparametric confidence intervals (also with casewise deletion).
```{r cfmissmeth}
h <- function() {
gc <- orm(gh ~ rcs(age,5) + re + rcs(leg,3) +
rcs(waist,4) + tri + rcs(sub,4),
family='loglog', data=w, x=TRUE, y=TRUE)
gb <- bootcov(gc, B=300)
list(gc=gc, gb=gb)
}
gbc <- runifChanged(h)
gc <- gbc$gc
gb <- gbc$gb
```
```{r peffects2,cap='Partial effect for age from multiple imputation and casewise deletion (center lines with the green line depicting all non-multiple-imputation methods) with symmetric Wald 0.95 confidence bands using casewise deletion, basic bootstrap confidence bands using casewise deletion, percentile bootstrap confidence bands using casewise deletion, and symmetric Wald confidence bands accounting for multiple imputation.',scap='Partial effect for age with bootstrap and Wald confidence bands',w=5,h=4}
#| label: fig-cony-peffects2
pgc <- Predict(gc, age)
bootclb <- Predict(gb, age, boot.type='basic')
bootclp <- Predict(gb, age, boot.type='percentile')
multimp <- Predict(g, age)
p <- rbind('casewise deletion' = pgc,
'basic bootstrap' = bootclb,
'percentile bootstrap' = bootclp,
'multiple imputation' = multimp)[, .q(age, yhat, lower, upper, .set.)]
m <- melt(as.data.table(p), id.vars=c('age', '.set.'))
ggplot(m, aes(x=age, y=value, color=.set.,
group=paste(variable, .set.))) + geom_line() +
guides(color=guide_legend(title='')) +
theme(legend.position='bottom') +
ylab(expression(X * hat(beta)))
```
In OLS `r ipacue()` the mean equals the median and both are linearly related to any
other quantiles. Semiparametric models are not this restrictive:
`r mrg(sound("ord-cont-11"))`
```{r meanvs,cap='Predicted mean `r hba` vs. predicted median and 0.9 quantile along with their marginal distributions',scap='Predicted mean, median, and 0.9 quantile of `r hba`',w=4.5,h=3.5}
#| label: fig-cony-meanvs
M <- Mean(g)
qu <- Quantile(g)
med <- function(lp) qu(.5, lp)
q90 <- function(lp) qu(.9, lp)
lp <- predict(g)
lpr <- quantile(predict(g), c(.002, .998), na.rm=TRUE)
lps <- seq(lpr[1], lpr[2], length=200)
pmn <- M(lps)
pme <- med(lps)
p90 <- q90(lps)
plot(pmn, pme,
xlab=expression(paste('Predicted Mean ', HbA["1c"])),
ylab='Median and 0.9 Quantile', type='l',
xlim=c(4.75, 8.0), ylim=c(4.75, 8.0), bty='n')
box(col=gray(.8))
lines(pmn, p90, col='blue')
abline(a=0, b=1, col=gray(.8))
text(6.5, 5.5, 'Median')
text(5.5, 6.3, '0.9', col='blue')
nint <- 350
scat1d(M(lp), nint=nint)
scat1d(med(lp), side=2, nint=nint)
scat1d(q90(lp), side=4, col='blue', nint=nint)
```
Draw a nomogram `r ipacue()` to compute 7 different predicted values for each
subject.
```{r nomogram,cap='Nomogram for predicting median, mean, and 0.9 quantile of glycohemoglobin, along with the estimated probability that $\\text{HbA}_{1c} \\ge 6.5, 7$, or $7.5$, all from the log-log ordinal model',scap='Nomogram of log-log ordinal model for $\\text{HbA}_{1c}$',w=6.75,h=6.25}
#| label: fig-cony-nomogram
spar(ps=9)
g <- Newlevels(g, list(re=abbreviate(levels(w$re))))
exprob <- ExProb(g)
nom <-
nomogram(g, fun=list(Mean=M,
'Median Glycohemoglobin' = med,
'0.9 Quantile' = q90,
'Prob(HbA1c >= 6.5)'=
function(x) exprob(x, y=6.5),
'Prob(HbA1c >= 7.0)'=
function(x) exprob(x, y=7),
'Prob(HbA1c >= 7.5)'=
function(x) exprob(x, y=7.5)),
fun.at=list(seq(5, 8, by=.5),
c(5,5.25,5.5,5.75,6,6.25),
c(5.5,6,6.5,7,8,10,12,14),
c(.01,.05,.1,.2,.3,.4),
c(.01,.05,.1,.2,.3,.4),
c(.01,.05,.1,.2,.3,.4)))
plot(nom, lmgp=.28)
```
```{r echo=FALSE}
saveCap('15')
```