Code
sr <- c(1.5, -1.5, 4, 3)
z <- sum(sr) / sqrt(sum(sr ^ 2))
pval <- 2 * (1 - pnorm(abs(z)))
c(z=z, pval=pval) z pval
1.2888045 0.1974661 1 The large-sample efficiency of the Wilcoxon and Spearman tests compared to \(t\) and \(r\) tests is \(\frac{3}{\pi} = 0.9549\).
| Group 1 | Group 2 | Means | \(P\) |
|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 | 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 5.5 and 13.5 | 0.000019 |
| 1 2 3 4 5 6 7 8 9 10 | 7 8 9 10 11 12 13 14 15 16 17 18 19 20 200 | 5.5 and 25.9 | 0.12 |
The SD is a particularly non-robust statistical estimator.
E.g., a CL for the difference in 2 means may include zero whereas the Wilcoxon test yields \(P=0.01\)
Point estimate that exactly corresponds to the Wilcoxon two-sample test is the Hodges-Lehman estimate of the location difference
| Parametric Test | Nonparametric Counterpart | Semiparametric Model Counterpart |
|---|---|---|
| 1-sample \(t\) | Wilcoxon signed-rank | |
| 2-sample \(t\) | Wilcoxon 2-sample rank-sum | Proportional odds |
| \(k\)-sample ANOVA | Kruskal-Wallis | Proportional odds |
| Pearson \(r\) | Spearman \(\rho\) |
| A | B | B-A | Rank \(|\mathrm{B-A}|\) | Signed Rank |
|---|---|---|---|---|
| 5 | 6 | 1 | 1.5 | 1.5 |
| 6 | 5 | -1 | 1.5 | -1.5 |
| 4 | 9 | 5 | 4.0 | 4.0 |
| 7 | 9 | 2 | 3.0 | 3.0 |
z pval
1.2888045 0.1974661 | Subject | Drug 1 | Drug 2 | Diff (2-1) | Sign | Rank | RD |
|---|---|---|---|---|---|---|
| 1 | 0.7 | 1.9 | 1.2 | + | 3 | 5 |
| 2 | -1.6 | 0.8 | 2.4 | + | 8 | 8.5 |
| 3 | -0.2 | 1.1 | 1.3 | + | 4.5 | 8 |
| 4 | -1.2 | 0.1 | 1.3 | + | 4.5 | 5 |
| 5 | -0.1 | -0.1 | 0.0 | NA | 0 | |
| 6 | 3.4 | 4.4 | 1.0 | + | 2 | 2.5 |
| 7 | 3.7 | 5.5 | 1.8 | + | 7 | 3 |
| 8 | 0.8 | 1.6 | 0.8 | + | 1 | 2.5 |
| 9 | 0.0 | 4.6 | 4.6 | + | 9 | 13.0 |
| 10 | 2.0 | 3.4 | 1.4 | + | 6 | 1.5 |
Wilcoxon signed rank test with continuity correction
data: drug2 and drug1
V = 45, p-value = 0.009091
alternative hypothesis: true location shift is not equal to 0
Wilcoxon signed rank test with continuity correction
data: drug2 - drug1
V = 45, p-value = 0.009091
alternative hypothesis: true location is not equal to 0
Wilcoxon signed rank test
data: drug2 - drug1
V = 45, p-value = 0.007632
alternative hypothesis: true location is not equal to 0 z pval
2.667911250 0.007632442 Test whether the continuity correction makes \(P\)-values closer to the exact calculation2
2 The exact \(P\)-value is available only when there are no ties.}, and compare to our simple formula.
# Assume we are already starting with signed ranks as x
wsr <- function(x, ...) wilcox.test(x, ...)$p.value
sim <- function(x) {
z <- sum(x) / sqrt(sum(x ^ 2))
2 * (1 - pnorm(abs(z))) }
alls <- function(x) round(c(
continuity=wsr(x, correct=TRUE, exact=FALSE),
nocontinuity=wsr(x, correct=FALSE, exact=FALSE),
exact=wsr(x, exact=TRUE),
simple=sim(x)), 4)
alls(1:4) continuity nocontinuity exact simple
0.1003 0.0679 0.1250 0.0679 continuity nocontinuity exact simple
0.2012 0.1441 0.2500 0.1441 continuity nocontinuity exact simple
0.3613 0.2733 0.3750 0.2733 continuity nocontinuity exact simple
0.2807 0.2249 0.3125 0.2249 continuity nocontinuity exact simple
0.4017 0.3454 0.4375 0.3454 From these examples the guidance is to:
wilcox.test) unlike the recommendation for the Pearson \(\chi^2\) testUnlike the Wilcoxon two-sample comparison, the Wilcoxon signed-rank test has a significant disadvantage in depending on how the response varible is transformed. The rank difference test of Kornbrot (1990)3 solves this problem. Kornbrot’s procedure is as follows
3 Also available here
The test is implemented in the R rankdifferencetest package by Brett Klamer4 but the essence of the calculation is below where we run the rank difference test on the data analyzed previously. The rank differences RD are shown in the data table there.
4 The rankdifferencetest package will provide exact p-values in case of ties.
Wilcoxon signed rank test with continuity correction
data: rank.diffs
V = 45, p-value = 0.00903
alternative hypothesis: true location is not equal to 0The results were identical to the signed-rank test because every subject had a higher drug 2 response than their drug 1 response except for the one that was tied which is excluded from both analyses.
| Females | 120 | 118 | 121 | 119 |
| Males | 124 | 120 | 133 | |
| Ranks for Females | 3.5 | 1 | 5 | 2 |
| Ranks for Males | 6 | 3.5 | 7 |
Doing a 2-sample \(t\)-test using these ranks as if they were raw data and computing the \(P\)-value against 4+3-2=5 d.f. will work quite well
Some statistical packages compute \(P\)-values exactly (especially if there are no ties)
Loosely speaking the WMW test tests whether the population medians of the two groups are the same
More accurately and more generally, it tests whether observations in one population tend to be larger than observations in the other
Letting \(x_1\) and \(x_2\) respectively be randomly chosen observations from populations one and two, WMW tests \(H_{0}:c=\frac{1}{2}\), where \(c=\)Prob\([x_{1} > x_{2}]\)
The \(c\) index (concordance probability) may be estimated by computing \[c = \frac{\bar{R}-\frac{n_{1}+1}{2}}{n_{2}},\] where \(\bar{R}\) is the mean of the ranks in group 1;
For the above data \(\bar{R} = 2.875\) and \(c=\frac{2.875-2.5}{3}=0.125\), so we estimate that the probability is 0.125 that a randomly chosen female has a value greater than a randomly chosen male.
In diagnostic studies where \(x\) is the continuous result of a medical test and the grouping variable is diseased vs. non-diseased, \(c\) is the area under the receiver operating characteristic (ROC) curve
Test still has the “probability of ordering” interpretation when the variances of the two samples are markedly different, but it no longer tests anything like the difference in population medians If there is no overlap between measurements from group 1 and those from group 2, the exact 2-sided \(P\)-value for the Wilcoxon test is \(2/ \frac{n!}{n_{1}! n_{2}!}\). If \(n_{1}=n_{2}\), \(n_{1}\) must be \(\geq 4\) to obtain \(P < 0.05\) (in this case \(P = 0.029\)).
#Fecal Calprotectin: 2500 is above detection limit
calpro <- c(2500, 244, 2500, 726, 86, 2500, 61, 392, 2500, 114, 1226,
2500, 168, 910, 627, 2500, 781, 57, 483, 30, 925, 1027,
2500, 2500, 38, 18)
# Endoscopy score: 1 = No/Mild, 2=Mod/Severe Disease
# Would have been far better to code dose as 4 ordinal levels
endo <- c(2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 2,
2, 2, 2, 2, 2, 1, 1)
endo <- factor(endo, 1 : 2,
c("No or Mild Activity", "Moderate or Severe Activity"))
require(ggplot2)
ggplot(data.frame(endo, calpro), aes(y=calpro, x=endo)) +
geom_boxplot(color='lightblue', alpha=.85, width=.4) +
geom_dotplot(binaxis='y', stackdir='center', position='dodge') +
xlab('') + ylab('Fecal Calprotectin') + coord_flip() +
geom_hline(aes(yintercept=2500, col=I('red')), linetype='dotted')
wilcox.test(calpro ~ endo)
Wilcoxon rank sum test with continuity correction
data: calpro by endo
W = 23.5, p-value = 0.006814
alternative hypothesis: true location shift is not equal to 0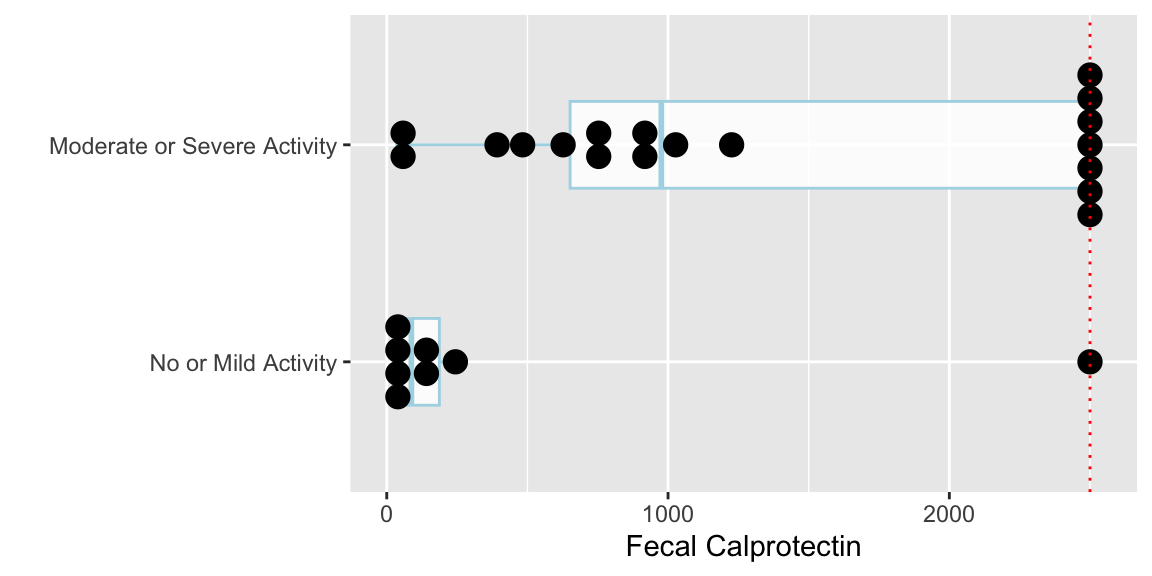
The following plots the ranks that are used in the Wilcoxon-Mann-Whitney two-sample rank sum test.
R somers2 function shows how the concordance probability is computed from the mean of the ranks in one of the two groups. C Dxy n Missing
0.8368056 0.6736111 26.0000000 0.0000000 If you type somers2 to list the code for the function you will see that the \(c\)-index is tightly related to the Wilcoxon test when you see this code:
As mentioned earlier, the effect estimate that is exactly consistent with the Wilcoxon two-sample test is the robust Hodges-Lehman estimator—the median of all possible differences between a measurement from group 1 and a measurement from group 2. There is a confidence interval for this estimator.
| Female \(\rightarrow\) | ||||
|---|---|---|---|---|
| Male \(\downarrow\) | 120 | 118 | 121 | 119 |
| 124 | 4 | 6 | 3 | 5 |
| 120 | 0 | 2 | -1 | 1 |
| 133 | 13 | 15 | 12 | 14 |
[,1] [,2] [,3] [,4]
[1,] 4 6 3 5
[2,] 0 2 -1 1
[3,] 13 15 12 14[1] 4.5
Wilcoxon rank sum test with continuity correction
data: male and female
W = 10.5, p-value = 0.1536
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-1 15
sample estimates:
difference in location
4.791134 In general, \(1 - \alpha\) confidence intervals are the set of values that if hypothesized to be the true location parameter would not be rejected at the \(\alpha\) level. wilcox.test computes the location shift by solving for the hypothesized value that yields \(P=1.0\) instead of the more proper median of all differences. Look into this further by plotting the \(P\)-value as a function of the hypothesized value.
dif <- seq(-3, 15, by=.1)
n <- length(dif)
pval <- numeric(n)
for(i in 1 : n) pval[i] <- wilcox.test(male - dif[i], female)$p.value
ggplot(data.frame(dif, pval), aes(x=dif, y=pval)) +
geom_step() +
geom_hline(yintercept=.05, col='red', linetype='dotted') +
geom_vline(xintercept=c(4.5, 4.791, -1, 15), col='red', linetype='dotted') +
xlab('Difference') + ylab('P-value')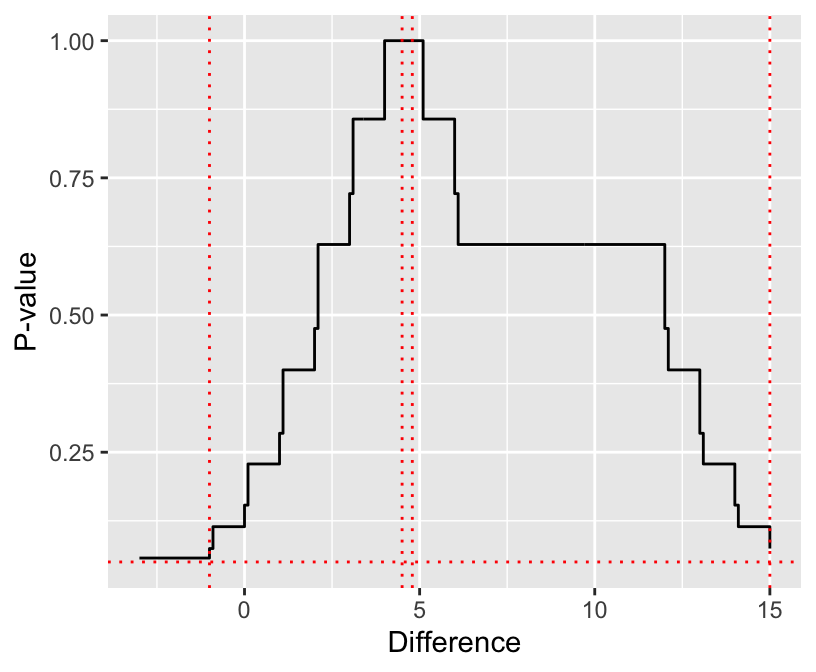
wilcox.test, the median difference, the Hodges-Lehman estimator as computed by wilcox.test, and the upper 0.95 confidence limit from wilcox.test.
See Section 7.4 for a more approximate confidence interval.
# Exact CI for median from DescTools package SignTest.default
# See also ttp://www.stat.umn.edu/geyer/old03/5102/notes/rank.pdf,
# http://de.scribd.com/doc/75941305/Confidence-Interval-for-Median-Based-on-Sign-Test
cimed <- function(x, alpha=0.05, na.rm=FALSE) {
if(na.rm) x <- x[! is.na(x)]
n <- length(x)
k <- qbinom(p=alpha / 2, size=n, prob=0.5, lower.tail=TRUE)
## Actual CL: 1 - 2 * pbinom(k - 1, size=n, prob=0.5) >= 1 - alpha
sort(x)[c(k, n - k + 1)]
}
cimed(1 : 100)[1] 40 61For \(n=100\) we see that the approximate interval happened to be exact.
wilcox.test).diffs <- numeric(1000)
set.seed(13)
for(i in 1 : 1000) diffs[i] <-
median(sample(male, replace=TRUE)) - median(sample(female, replace=TRUE))
ggplot(data.frame(diffs), aes(x=diffs)) + xlab('Differences in Medians') +
geom_histogram(bin_widith=.01, color='blue', fill='white')
quantile(diffs, c(0.025, 0.975)) 2.5% 97.5%
-0.5 14.5 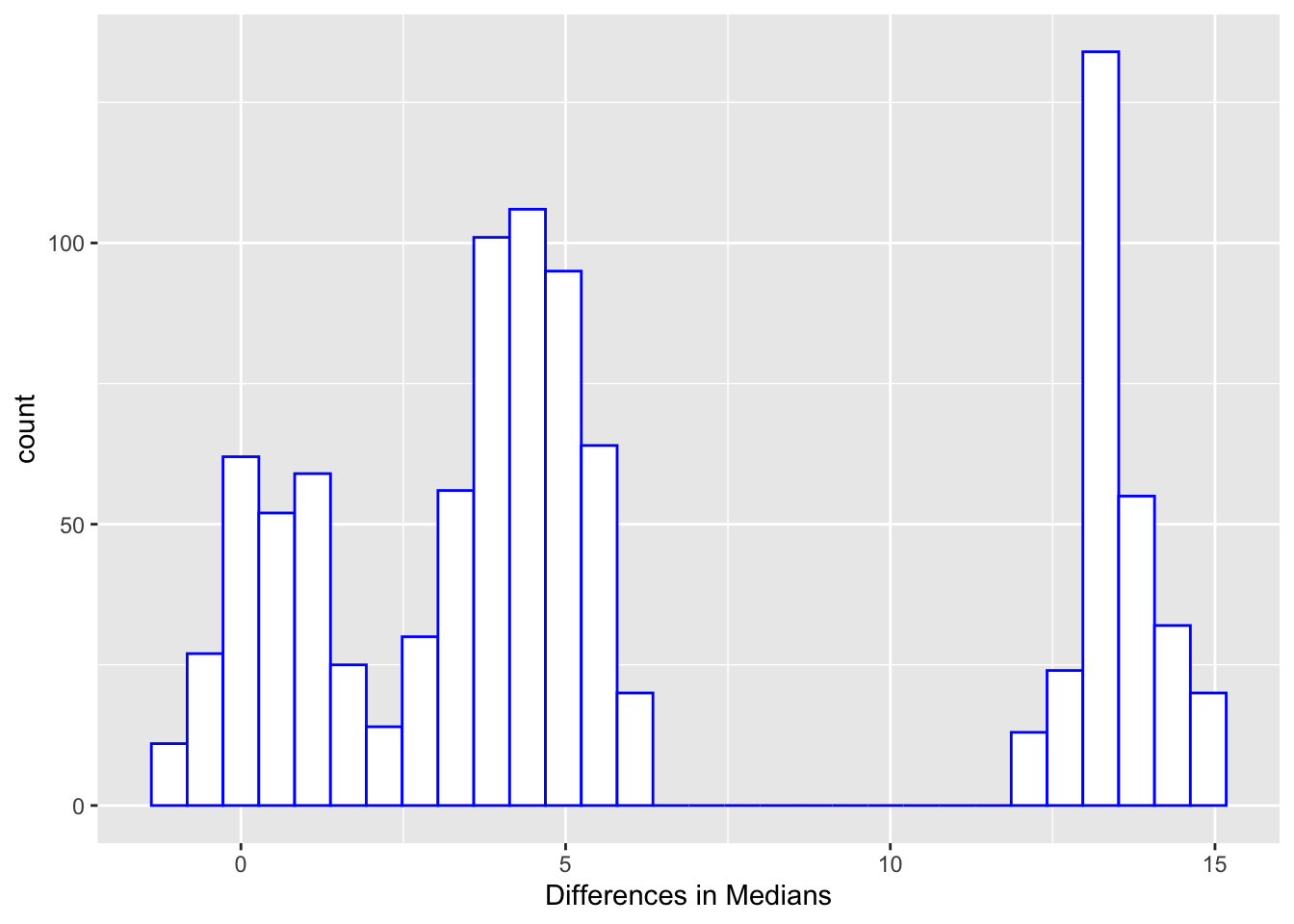
But recall that the Wilcoxon test does not really test the difference in medians but rather the median of all differences.
5 A good nonparametric confidence for a population mean that does not even assume a symmetric distribution can be obtained from the bootstrap simulation procedure.
R rms package orm function fits the PO model7 and is especially made for continuous \(Y\), with fast run times for up to 6000 intercepts6 When using the Kruskal-Wallis test followed by pairwise Wilcoxon tests, these pairwise tests can be inconsistent with each other, because they re-rank the data based only on two groups, destroying the transitivity property, e.g. treatment A can be better than B which is better than C but C is better than A.
7 orm also fits other models using link functions other than the logit.
8 The predicted mean for a set of covariate settings is obtained by using all the intercepts and \(\beta\)s to get exceedance probabilities for \(Y \geq y\), taking successive differences in those probabilities to get cell probabilities that \(Y=y\), then multiplying cell probabilities by the \(y\) value attached to them, and summing. This is the formula for the mean for a discrete distribution.
Logistic (Proportional Odds) Ordinal Regression Model
orm(formula = y ~ group)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 400 | LR χ2 193.31 | R2 0.383 | ρ 0.633 |
| ESS 400 | d.f. 3 | R23,400 0.379 | Dxy 0.426 |
| Distinct Y 400 | Pr(>χ2) <0.0001 | R23,400 0.379 | |
| Y0.5 115.4143 | Score χ2 193.21 | |Pr(Y ≥ median)-½| 0.256 | |
| max |∂log L/∂β| 3×10-11 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| group=B | 1.4221 | 0.2579 | 5.51 | <0.0001 |
| group=C | 2.6624 | 0.2762 | 9.64 | <0.0001 |
| group=D | 3.6606 | 0.2925 | 12.52 | <0.0001 |
group yhat lower upper
1 A 99.32328 96.46657 102.1800
2 B 111.21326 108.27169 114.1548
3 C 121.63880 118.78670 124.4909
4 D 129.70290 127.07203 132.3338
Response variable (y):
Limits are 0.95 confidence limits group y Lower Upper
1 A 98.72953 95.81508 101.6440
2 B 111.69464 108.61130 114.7780
3 C 121.80841 118.93036 124.6865
4 D 130.05275 127.40318 132.7023 Contrast S.E. Lower Upper Z Pr(>|z|)
11 1.240366 0.2564632 0.7377076 1.743025 4.84 0
Confidence intervals are 0.95 individual intervals Contrast Lower Upper Z Pr(>|z|)
11 3.45688 2.091136 5.714604 4.84 0
Confidence intervals are 0.95 individual intervalsLogistic (Proportional Odds) Ordinal Regression Model
orm(formula = calpro ~ endo)
Frequencies of Responses
18 30 38 57 61 86 114 168 244 392 483 627 726 781 910 925 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1027 1226 2500 1 1 8
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 26 | LR χ2 9.84 | R2 0.317 | ρ 0.547 |
| ESS 25.2 | d.f. 1 | R21,26 0.288 | Dxy 0.327 |
| Distinct Y 19 | Pr(>χ2) 0.0017 | R21,25.2 0.296 | |
| Y0.5 753.5 | Score χ2 9.86 | |Pr(Y ≥ median)-½| 0.251 | |
| max |∂log L/∂β| 4×10-14 | Pr(>χ2) 0.0017 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| y≥30 | 2.0969 | 1.0756 | 1.95 | 0.0512 |
| y≥38 | 1.3395 | 0.8160 | 1.64 | 0.1007 |
| y≥57 | 0.8678 | 0.7135 | 1.22 | 0.2239 |
| y≥61 | 0.4733 | 0.6689 | 0.71 | 0.4792 |
| y≥86 | 0.1122 | 0.6575 | 0.17 | 0.8645 |
| y≥114 | -0.1956 | 0.6558 | -0.30 | 0.7655 |
| y≥168 | -0.4710 | 0.6608 | -0.71 | 0.4760 |
| y≥244 | -0.7653 | 0.6868 | -1.11 | 0.2652 |
| y≥392 | -1.0953 | 0.7427 | -1.47 | 0.1403 |
| y≥483 | -1.4155 | 0.8015 | -1.77 | 0.0774 |
| y≥627 | -1.6849 | 0.8383 | -2.01 | 0.0445 |
| y≥726 | -1.9227 | 0.8641 | -2.23 | 0.0261 |
| y≥781 | -2.1399 | 0.8836 | -2.42 | 0.0154 |
| y≥910 | -2.3439 | 0.8993 | -2.61 | 0.0092 |
| y≥925 | -2.5396 | 0.9128 | -2.78 | 0.0054 |
| y≥1027 | -2.7312 | 0.9249 | -2.95 | 0.0031 |
| y≥1226 | -2.9224 | 0.9365 | -3.12 | 0.0018 |
| y≥2500 | -3.1166 | 0.9482 | -3.29 | 0.0010 |
| endo=Moderate or Severe Activity | 2.7586 | 0.9576 | 2.88 | 0.0040 |
9 The intercepts really represent the logit of one minus the CDF, moved one \(Y\) value.
Effects Response: calpro |
|||||||
| Low | High | Δ | Effect | S.E. | Lower 0.95 | Upper 0.95 | |
|---|---|---|---|---|---|---|---|
| endo --- Moderate or Severe Activity:No or Mild Activity | 1 | 2 | 2.759 | 0.9576 | 0.8818 | 4.635 | |
| Odds Ratio | 1 | 2 | 15.780 | 2.4150 | 103.100 | ||
endo=Moderate or Severe Activity
0.8567819 Compare this to the exact value of 0.837.
Predict() see the point estimates under yhat, starting with the estimates for \(P(Y \geq 2500)\), i.e., marker value at or above the upper detection limit endo yhat lower upper
1 No or Mild Activity 0.04242913 0.008080662 0.1941978
2 Moderate or Severe Activity 0.41144481 0.209594384 0.6482556
Response variable (y):
Limits are 0.95 confidence limits No or Mild Activity Moderate or Severe Activity
0.1250000 0.3888889 endo yhat lower upper
1 No or Mild Activity 300.2578 0.3895958 600.126
2 Moderate or Severe Activity 1387.6603 947.0114887 1828.309
Response variable (y):
Limits are 0.95 confidence limits No or Mild Activity Moderate or Severe Activity
400.000 1372.944 endo yhat lower upper
1 No or Mild Activity 82.20742 25.72648 574.9765
2 Moderate or Severe Activity 1038.80796 622.73997 2500.0000
Response variable (y):
Limits are 0.95 confidence limits No or Mild Activity Moderate or Severe Activity
87.5 976.0 Note: confidence intervals for these derived quantities are approximate
Compute estimated median for every subject
As a measure of predictive strength compute the mean absolute difference between predicted median and observed raw values
Compare this to the mean absolute difference between a constant prediction (the overall median) and predicted medians
[1] 679.5622[1] 839.4231Running MCMC with 4 chains, at most 9 in parallel...
Chain 1 finished in 0.1 seconds.
Chain 2 finished in 0.1 seconds.
Chain 3 finished in 0.1 seconds.
Chain 4 finished in 0.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.1 seconds.
Total execution time: 0.2 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.134 for Intercepts
blrm(formula = calpro ~ endo)
Frequencies of Responses
18 30 38 57 61 86 114 168 244 392 483 627 726 781 910 925 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1027 1226 2500 1 1 8
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 26 | LOO log L -96.21±9.02 | g 1.303 [0.528, 2.19] | C 0.854 [0.854, 0.854] |
| Draws 4000 | LOO IC 192.43±18.03 | gp 0.051 [0, 0.14] | Dxy 0.708 [0.708, 0.708] |
| Chains 4 | Effective p 33.13±4.15 | EV 0.072 [0, 0.208] | |
| Time 0.4s | B 0.037 [0.034, 0.047] | v 2.125 [0.023, 4.809] | |
| p 1 | vp 0.005 [0, 0.022] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry |
|---|---|---|---|---|---|---|---|
| 2.7591 | 2.9417 | 2.9173 | 0.9770 | 1.0364 | 4.8549 | 0.9992 | 1.06 |
pmed pmedb
1 1038.80796 922.7636
2 82.20742 62.4170
3 1038.80796 922.7636
4 1038.80796 922.7636
5 1038.80796 922.7636
6 82.20742 62.4170
7 82.20742 62.4170
8 1038.80796 922.7636
9 1038.80796 922.7636
10 82.20742 62.4170
11 1038.80796 922.7636
12 1038.80796 922.7636
13 82.20742 62.4170
14 1038.80796 922.7636
15 1038.80796 922.7636
16 1038.80796 922.7636
17 1038.80796 922.7636
18 82.20742 62.4170
19 1038.80796 922.7636
20 1038.80796 922.7636
21 1038.80796 922.7636
22 1038.80796 922.7636
23 1038.80796 922.7636
24 1038.80796 922.7636
25 82.20742 62.4170
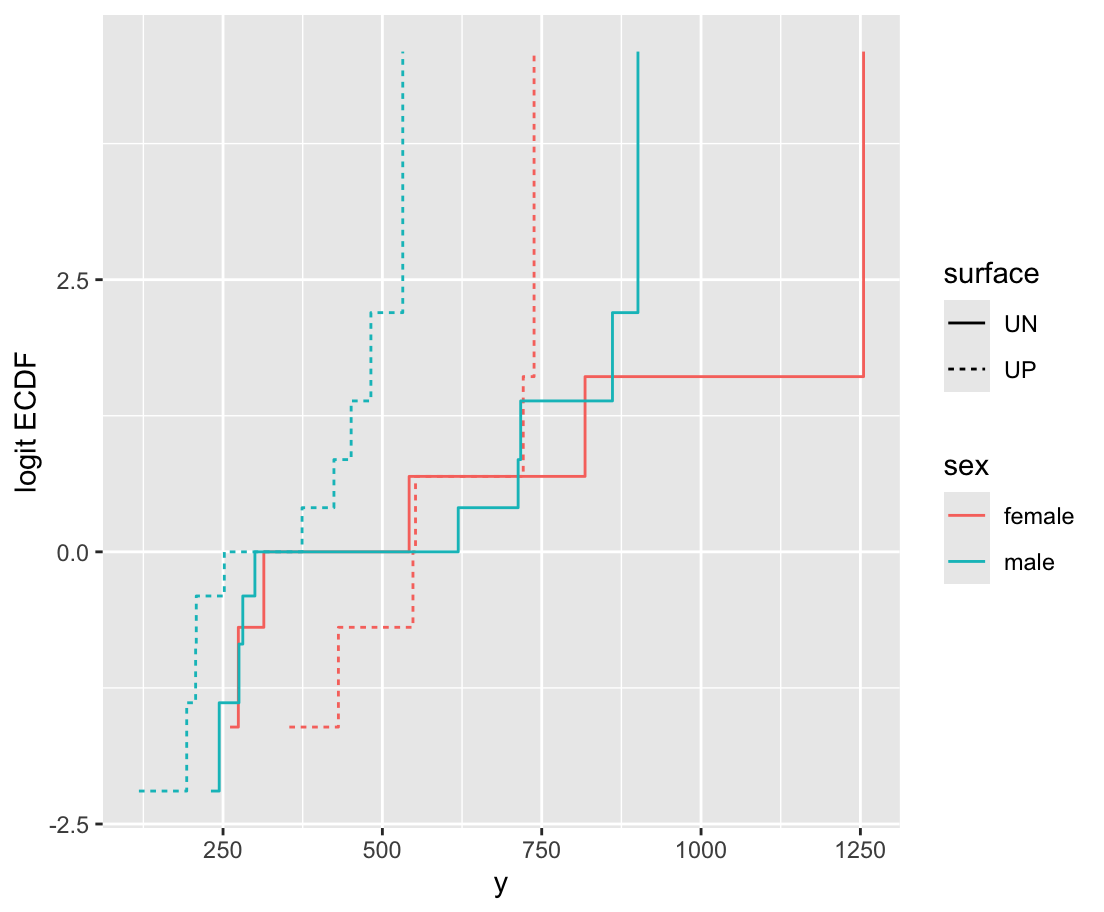
26 82.20742 62.4170[1] 678.8259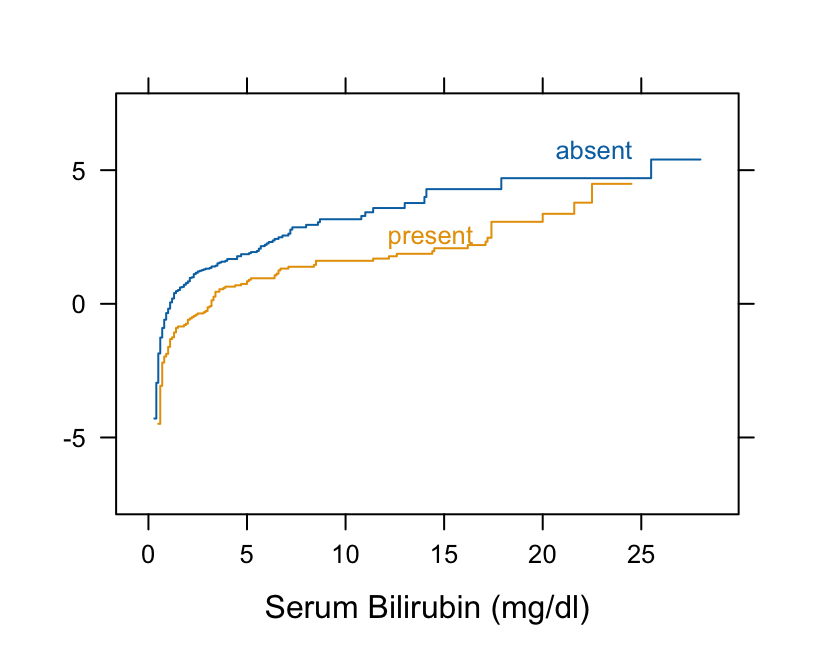
d <- csv.get(textConnection('
id sex surface y
1 female UN 1255
2 female UN 542
3 female UN 818
1 female UN 274
2 female UN 261
3 female UN 314
1 female UP 552
2 female UP 548
3 female UP 721
1 female UP 431
2 female UP 354
3 female UP 738
4 male UN 901
5 male UN 619
6 male UN 861
7 male UN 713
8 male UN 717
4 male UN 275
5 male UN 300
6 male UN 244
7 male UN 281
8 male UN 231
4 male UP 532
5 male UP 451
6 male UP 482
7 male UP 374
8 male UP 424
4 male UP 193
5 male UP 118
6 male UP 207
7 male UP 208
8 male UP 252
'), sep='\t')
require(data.table)
setDT(d)\t is the tab character
data.frame into a data.table
ecdfSteps is in the Hmisc package; it computes coordinates of empirical cumulative distribution functions; data.table uses by= for stratification
orm is the rms package’s function for analyzing continuous responses as ordinal. It also works for discrete Y but the rms lrm function is sometimes better for that. x=TRUE, y=TRUE is for getting likelihood ratio \(\chi^2\) tests.
Logistic (Proportional Odds) Ordinal Regression Model
orm(formula = y ~ sex + surface, data = d, x = TRUE, y = TRUE)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 32 | LR χ2 4.67 | R2 0.136 | ρ 0.395 |
| ESS 32 | d.f. 2 | R22,32 0.080 | Dxy 0.258 |
| Distinct Y 32 | Pr(>χ2) 0.0966 | R22,32 0.080 | |
| Y0.5 427.5 | Score χ2 4.54 | |Pr(Y ≥ median)-½| 0.137 | |
| max |∂log L/∂β| 2×10-11 | Pr(>χ2) 0.1036 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| y≥193 | 4.8126 | 1.2445 | 3.87 | 0.0001 |
| y≥207 | 4.0573 | 1.0130 | 4.01 | <0.0001 |
| y≥208 | 3.5856 | 0.9134 | 3.93 | <0.0001 |
| y≥231 | 3.2269 | 0.8502 | 3.80 | 0.0001 |
| y≥244 | 2.9369 | 0.8066 | 3.64 | 0.0003 |
| y≥252 | 2.6958 | 0.7774 | 3.47 | 0.0005 |
| y≥261 | 2.4797 | 0.7531 | 3.29 | 0.0010 |
| y≥274 | 2.2864 | 0.7327 | 3.12 | 0.0018 |
| y≥275 | 2.1194 | 0.7194 | 2.95 | 0.0032 |
| y≥281 | 1.9677 | 0.7101 | 2.77 | 0.0056 |
| y≥300 | 1.8238 | 0.7031 | 2.59 | 0.0095 |
| y≥314 | 1.6858 | 0.6981 | 2.41 | 0.0157 |
| y≥354 | 1.5559 | 0.6956 | 2.24 | 0.0253 |
| y≥374 | 1.4342 | 0.6955 | 2.06 | 0.0392 |
| y≥424 | 1.3127 | 0.6954 | 1.89 | 0.0591 |
| y≥431 | 1.1861 | 0.6937 | 1.71 | 0.0873 |
| y≥451 | 1.0580 | 0.6920 | 1.53 | 0.1263 |
| y≥482 | 0.9273 | 0.6902 | 1.34 | 0.1791 |
| y≥532 | 0.7877 | 0.6863 | 1.15 | 0.2511 |
| y≥542 | 0.6365 | 0.6795 | 0.94 | 0.3489 |
| y≥548 | 0.4821 | 0.6742 | 0.71 | 0.4746 |
| y≥552 | 0.3286 | 0.6732 | 0.49 | 0.6255 |
| y≥619 | 0.1697 | 0.6743 | 0.25 | 0.8013 |
| y≥713 | 0.0003 | 0.6775 | 0.00 | 0.9996 |
| y≥717 | -0.1863 | 0.6830 | -0.27 | 0.7850 |
| y≥721 | -0.3969 | 0.6917 | -0.57 | 0.5661 |
| y≥738 | -0.6380 | 0.7055 | -0.90 | 0.3658 |
| y≥818 | -0.9211 | 0.7283 | -1.26 | 0.2060 |
| y≥861 | -1.2581 | 0.7754 | -1.62 | 0.1047 |
| y≥901 | -1.7012 | 0.8727 | -1.95 | 0.0512 |
| y≥1255 | -2.4509 | 1.1155 | -2.20 | 0.0280 |
| sex=male | -1.2211 | 0.6677 | -1.83 | 0.0674 |
| surface=UP | -0.7824 | 0.6446 | -1.21 | 0.2249 |
Likelihood Ratio Statistics for y |
|||
| χ2 | d.f. | P | |
|---|---|---|---|
| sex | 3.47 | 1 | 0.0625 |
| surface | 1.50 | 1 | 0.2210 |
| TOTAL | 4.67 | 2 | 0.0966 |
yM <- Mean(f)
qu <- Quantile(f)
med <- function(lp) qu(0.5, lp)
g <- function(x) list(Mean=mean(x), Median=median(x))
cat('Sample estimates\n')
d[, g(y), by=.(sex, surface)]
cat('\nModel estimates of means (yhat)\n')
Predict(f, surface, sex=.q(female, male), fun=M)
cat('\nModel estimates of medians (yhat)\n')
Predict(f, surface, sex=.q(female, male), fun=med)fun=... causes predicted log odds to be transformed by the named function; .q is an R Hmisc package function that quotes strings for you
Sample estimates
sex surface Mean Median
<char> <char> <num> <num>
1: female UN 577.3333 428.0
2: female UP 557.3333 550.0
3: male UN 514.2000 459.5
4: male UP 324.1000 313.0
Model estimates of means (yhat)
surface sex yhat lower upper
1 UN female 640.6769 443.1609 838.1930
2 UP female 523.7141 365.5194 681.9088
3 UN male 463.0476 324.4904 601.6048
4 UP male 368.6684 259.6604 477.6763
Response variable (y):
Limits are 0.95 confidence limits
Model estimates of medians (yhat)
surface sex yhat lower upper
1 UN female 669.7487 384.5832 856.3839
2 UP female 508.5185 279.8697 718.9219
3 UN male 419.3042 264.8156 613.7942
4 UP male 277.0920 227.9898 463.4451
Response variable (y):
Limits are 0.95 confidence limitsJust as a binary logistic model may be used to do the McNemar test for paired binary data, regression can be used for testing for effects in paired ordinal or continuous data. Regression is more general:
Can adjust for covariates
Can have more than 2 (pre, post) periods, e.g., handles a multi-period crossover study
Paired \(t\)-test is equivalent to
Rank difference test is similar to
Let’s illustrate this by re-analyzing paired data analyzed previously.
Paired t-test
data: drug1 and drug2
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean difference
-1.58 [1] 0.3889587Linear Regression Model
ols(formula = y ~ drug + id)
| Model Likelihood Ratio Test |
Discrimination Indexes |
|
|---|---|---|
| Obs 20 | LR χ2 48.61 | R2 0.912 |
| σ 0.8697 | d.f. 10 | R2adj 0.814 |
| d.f. 9 | Pr(>χ2) 0.0000 | g 2.248 |
Residuals
Min 1Q Median 3Q Max -1.510e+00 -2.150e-01 -6.939e-18 2.150e-01 1.510e+00
| β | S.E. | t | Pr(>|t|) | |
|---|---|---|---|---|
| Intercept | 0.5100 | 0.6450 | 0.79 | 0.4495 |
| drug=B | 1.5800 | 0.3890 | 4.06 | 0.0028 |
| id=2 | -1.7000 | 0.8697 | -1.95 | 0.0824 |
| id=3 | -0.8500 | 0.8697 | -0.98 | 0.3540 |
| id=4 | -1.8500 | 0.8697 | -2.13 | 0.0623 |
| id=5 | -1.4000 | 0.8697 | -1.61 | 0.1419 |
| id=6 | 2.6000 | 0.8697 | 2.99 | 0.0152 |
| id=7 | 3.3000 | 0.8697 | 3.79 | 0.0043 |
| id=8 | -0.1000 | 0.8697 | -0.11 | 0.9110 |
| id=9 | 1.0000 | 0.8697 | 1.15 | 0.2799 |
| id=10 | 1.4000 | 0.8697 | 1.61 | 0.1419 |
Linear mixed-effects model fit by REML
Data: d
AIC BIC logLik
77.95588 81.51737 -34.97794
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.6877 0.8697384
Fixed effects: y ~ drug
Value Std.Error DF t-value p-value
(Intercept) 0.75 0.6003979 9 1.249172 0.2431
drugB 1.58 0.3889588 9 4.062127 0.0028
Correlation:
(Intr)
drugB -0.324
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-1.63372282 -0.34157076 0.03346151 0.31510644 1.83858572
Number of Observations: 20
Number of Groups: 10 x=TRUE, y=TRUE needed for robcov, which is in the rms package
Linear Regression Model
ols(formula = y ~ drug, x = TRUE, y = TRUE)
| Model Likelihood Ratio Test |
Discrimination Indexes |
|
|---|---|---|
| Obs 20 | LR χ2 3.52 | R2 0.161 |
| σ 1.8986 | d.f. 1 | R2adj 0.115 |
| d.f. 18 | Pr(>χ2) 0.0607 | g 0.832 |
Cluster on id |
||
| Clusters 10 |
Residuals
Min 1Q Median 3Q Max -2.430 -1.305 -0.580 1.455 3.170
| β | S.E. | t | Pr(>|t|) | |
|---|---|---|---|---|
| Intercept | 0.7500 | 0.5367 | 1.40 | 0.1793 |
| drug=B | 1.5800 | 0.3690 | 4.28 | 0.0004 |
Standard error is a bit too small
P-value is too small because the sandwich estimator leads to a \(z\)-statistic and we should probably be using a \(t\)-statistic with the usual d.f.
Now compare rank difference test with PO model
Likelihood Ratio Statistics for y |
|||
| χ2 | d.f. | P | |
|---|---|---|---|
| drug | 22.33 | 1 | <0.0001 |
| id | 42.46 | 9 | <0.0001 |
| TOTAL | 46.27 | 10 | <0.0001 |
Cumulative Link Mixed Model fitted with the Laplace approximation
Call:
clmm2(location = factor(y) ~ drug, random = id, data = d, Hess = TRUE,
link = "logistic")
Random effects:
Var Std.Dev
id 9.965494 3.156817
Location coefficients:
Estimate Std. Error z value Pr(>|z|)
drugB 3.4639 0.0040 873.3616 < 2.22e-16
No scale coefficients
Threshold coefficients:
Estimate Std. Error z value
-1.6|-1.2 -4.7116 1.6232 -2.9027
-1.2|-0.2 -3.4748 1.4104 -2.4637
-0.2|-0.1 -2.5545 1.3280 -1.9236
-0.1|0 -1.0964 1.1884 -0.9226
0|0.1 -0.5557 1.1367 -0.4889
0.1|0.7 -0.1084 1.1091 -0.0977
0.7|0.8 0.3316 1.0951 0.3028
0.8|1.1 1.3985 1.0786 1.2966
1.1|1.6 2.0826 1.0414 1.9997
1.6|1.9 2.7146 0.9831 2.7614
1.9|2 3.2579 0.9314 3.4979
2|3.4 3.8834 0.8593 4.5191
3.4|3.7 5.3998 0.0038 1433.6040
3.7|4.4 6.2449 0.0040 1574.6075
4.4|4.6 7.1125 0.7138 9.9649
4.6|5.5 8.4414 0.0040 2128.3103
log-likelihood: -50.12908
AIC: 136.2582
Condition number of Hessian: 1091538.97 clmm2 uses a Laplace approximation for numerical integration. Let’s try using 7-point quadrature integration instead.
Cumulative Link Mixed Model fitted with the adaptive Gauss-Hermite
quadrature approximation with 7 quadrature points
Call:
clmm2(location = factor(y) ~ drug, random = id, data = d, Hess = TRUE,
link = "logistic", nAGQ = 7)
Random effects:
Var Std.Dev
id 9.7614 3.124324
Location coefficients:
Estimate Std. Error z value Pr(>|z|)
drugB 3.4093 1.2088 2.8205 0.0047942
No scale coefficients
Threshold coefficients:
Estimate Std. Error z value
-1.6|-1.2 -4.6254 1.8980 -2.4370
-1.2|-0.2 -3.4202 1.6540 -2.0678
-0.2|-0.1 -2.5169 1.5306 -1.6443
-0.1|0 -1.0695 1.3617 -0.7854
0|0.1 -0.5393 1.3192 -0.4088
0.1|0.7 -0.1034 1.3011 -0.0795
0.7|0.8 0.3309 1.2972 0.2551
0.8|1.1 1.3813 1.3552 1.0192
1.1|1.6 2.0516 1.4343 1.4304
1.6|1.9 2.6785 1.5130 1.7703
1.9|2 3.2211 1.5777 2.0417
2|3.4 3.8351 1.6946 2.2631
3.4|3.7 5.3411 2.0913 2.5539
3.7|4.4 6.1718 2.2910 2.6940
4.4|4.6 7.0214 2.4485 2.8677
4.6|5.5 8.3565 2.8343 2.9483
log-likelihood: -49.85619
AIC: 135.7124
Condition number of Hessian: 525.3332 Running MCMC with 4 chains, at most 9 in parallel...
Chain 1 finished in 0.2 seconds.
Chain 2 finished in 0.2 seconds.
Chain 3 finished in 0.2 seconds.
Chain 4 finished in 0.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.2 seconds.
Total execution time: 0.4 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.148 for Intercepts
blrm(formula = y ~ drug + cluster(id), data = d)
Frequencies of Responses
-1.6 -1.2 -0.2 -0.1 0 0.1 0.7 0.8 1.1 1.6 1.9 2 3.4 3.7 4.4 4.6 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1 1 5.5 1
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 20 | LOO log L -74.06±3.86 | g 1.571 [0.445, 2.783] | C 0.751 [0.753, 0.753] |
| Draws 4000 | LOO IC 148.11±7.73 | gp 0.015 [0, 0.058] | Dxy 0.503 [0.505, 0.505] |
| Chains 4 | Effective p 33.23±2.57 | EV 0.013 [0, 0.049] | |
| Time 0.6s | B 0.048 [0.045, 0.05] | v 2.667 [0.001, 6.472] | |
| p 1 | vp 0.001 [0, 0.003] | ||
Cluster on id |
|||
| Clusters 10 | |||
| σγ 2.2413 [0.3594, 4.2682] |
| Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry |
|---|---|---|---|---|---|---|
| 2.9207 | 2.8320 | 1.1041 | 0.9770 | 5.3064 | 0.9990 | 1.24 |
beta se z p Pr(beta > 0)
2.921 1.104 2.645 0.008 0.999 Compare the p=0.007 with the rank difference tests’s p=0.009
Note that \(\beta\) is on the log-odds scale and cannot be compared to a difference in means
Semiparametric models can be used to estimate means, quantiles, etc. (Section 7.8)
Try an ordinary PO model with a cluster sandwich covariance estimator
Logistic (Proportional Odds) Ordinal Regression Model
orm(formula = y ~ drug, x = TRUE, y = TRUE)
Frequencies of Responses
-1.6 -1.2 -0.2 -0.1 0 0.1 0.7 0.8 1.1 1.6 1.9 2 3.4 3.7 4.4 4.6 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1 1 5.5 1
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 20 | LR χ2 3.82 | R2 0.174 | ρ 0.425 |
| ESS 19.9 | d.f. 1 | R21,20 0.131 | Dxy 0.262 |
| Distinct Y 17 | Pr(>χ2) 0.0507 | R21,19.9 0.132 | |
Cluster on id |
Score χ2 3.74 | |Pr(Y ≥ median)-½| 0.183 | |
| Clusters 10 | Pr(>χ2) 0.0531 | ||
| Y0.5 0.95 | |||
| max |∂log L/∂β| 2×10-14 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| drug=B | 1.5916 | 0.4831 | 3.29 | 0.0010 |
n: 10 r2: 0.9923288
n: 100 r2: 0.9688625
n: 1000 r2: 0.958053
n: 10000 r2: 0.9554628
n: 1e+05 r2: 0.955008
n: 1e+06 r2: 0.9549402 3/pi: 0.9549297 R Hmisc package popower and posamsize functionsPower: 0.516
Efficiency of design compared with continuous response: 0.966
Approximate standard error of log odds ratio: 0.1116 Total sample size: 2621.4
Efficiency of design compared with continuous response: 0.966 [1] 0.25531915 0.09250694 0.09661836 0.10101010 0.10570825 0.11074197 0.11614402
[8] 0.12195122[1] 12.7
OR mean median
1 12.70000 3.000000
1.05 13.14602 3.364286
1.1 13.58143 3.709091
1.2 14.42238 4.350000
1.25 14.82881 4.650000
1.5 16.73559 6.000000
2 20.03640 9.900000
Two-sample t test power calculation
n = 150
d = 0.3
sig.level = 0.05
power = 0.7355674
alternative = two.sided
NOTE: n is number in *each* groupgetRs('hashCheck.r') # defines runifChanged
s <- 1000 # number of simulated trials
pval <- numeric(s)
set.seed(1) # so can reproduce results
for(i in 1 : s) {
y1 <- rnorm(150, 100, 10)
y2 <- rnorm(150, 103, 10)
w <- wilcox.test(y1, y2)
pval[i] <- w$p.value
}
mean(pval < 0.05) # proportion of simulations with p < 0.05[1] 0.713[1] 0.71[1] 1.706672ggplot(mapping=aes(ors, means)) + geom_line() +
geom_hline(yintercept=103, alpha=I(0.25)) +
geom_vline(xintercept=needed.or, alpha=I(0.25)) +
xlab('Group B:A Odds Ratio') +
ylab('Mean in Population B')
# Compute power at that odds ratio assuming no ties in data
popower(rep(1/300, 300), odds.ratio=needed.or, n=300)Power: 0.759
Efficiency of design compared with continuous response: 1
Approximate standard error of log odds ratio: 0.2007 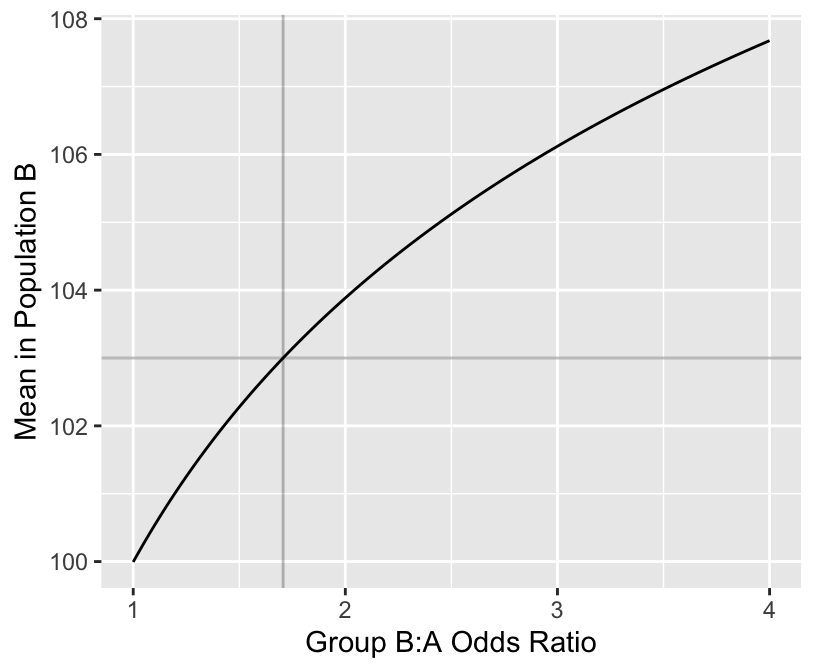
# First do this theoretically
# Control arm has Gaussian Y with mean 100, SD 10
# Create experimental arm distribution using OR=10
y <- seq(60, 145, length=150)
Fy <- 1 - pnorm(y, mean=100, sd=10) # P(Y >= y | group A)
Gy <- 1 - plogis(qlogis(Fy) + log(10)) # P(Y >= y | group B)
qu <- approx(Gy, y, xout=c(0.25, 0.5, 0.75))$y
qu # Q1, median, Q2[1] 107.3628 113.3506 118.4894s <- (qu[3] - qu[1]) / (qnorm(0.75) - qnorm(0.25))
mu <- qu[1] - s * qnorm(0.25)
ncdf <- pnorm(y, mean=mu, sd=s)
d <- rbind(data.frame(Distribution='logistic', x=y, y=Gy),
data.frame(Distribution='normal', x=y, y=ncdf))
ggplot(d, aes(x, y, col=Distribution)) + geom_line() +
xlab(expression(y)) + ylab(expression(P(Y <= y)))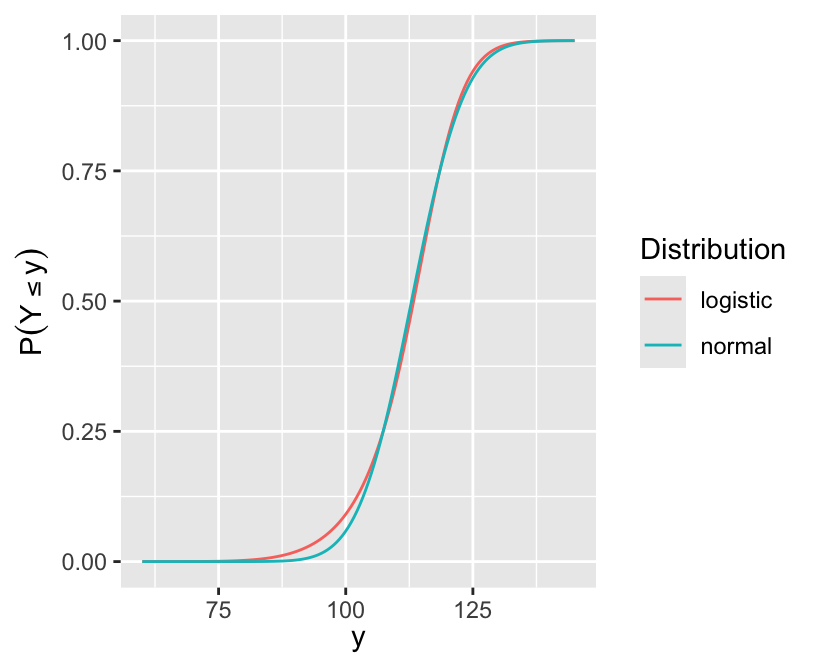
[1] 5.000023e-07 4.999773e-05[1] 112.4071[1] 112.4658 25% 50% 75%
107.4406 113.3427 118.4725 
s <- 1000 # number of simulated trials
pvalt <- pvalw <- numeric(s)
set.seed(1) # so can reproduce results
for(delta in c(0, 0.3)) {
for(i in 1 : s) {
y1 <- rt(150, 4)
y2 <- rt(150, 4) + delta
pvalt[i] <- t.test(y1, y2)$p.value
pvalw[i] <- wilcox.test(y1, y2)$p.value
}
cat('Delta:', delta, '\n')
P <- function(x) round(mean(x), 2)
cat('Proportion of simulations with W p-value < t p-value:',
P(pvalw < pvalt), '\n')
cat('Mean p-value for t:', P(pvalt), '\n')
cat('Mean p-value for W:', P(pvalw), '\n')
cat('Power for t:', P(pvalt < 0.05), '\n')
cat('Power for W:', P(pvalw < 0.05), '\n\n')
}Delta: 0
Proportion of simulations with W p-value < t p-value: 0.51
Mean p-value for t: 0.5
Mean p-value for W: 0.49
Power for t: 0.05
Power for W: 0.06
Delta: 0.3
Proportion of simulations with W p-value < t p-value: 0.73
Mean p-value for t: 0.17
Mean p-value for W: 0.12
Power for t: 0.47
Power for W: 0.6 Hmisc simRegOrd function can also simulate power for an adjusted two-sample comparison if there is one adjustment covariateblrm function in the R rmsb package is devoted to the PO and partial PO modelR brms package: bit.ly/brms-ordinal and this discussion:10 One merely takes each posterior sample for the \(\alpha\)s and \(\beta\)s and computes the quantity of interest, thereby automatically generating posterior samples for the derived quantity for which quantiles can compute credible intervals, etc.
The empirical cumulative distribution function (ECDF) was introduced in Section 4.3.3.2. It is a nonparametric estimator of the unknown CDF for a (primarily) continuous variable. Inverting the ECDF gives traditional sample quantile estimates, so if one wants to estimate all possible quantiles accurately one needs to estimate the ECDF accurately over its entire range.
Kolmogorov and Smirnov developed a nonparametric test for whether a sample comes from a specific parametric CDF, by computing the maximum absolute difference between the ECDF and the postulated CDF. This test can be inverted to obtain simultaneous confidence bands for the unknown CDF. The global margin of error for an ECDF is the Kolmogorov-Smirnov critical value, for a certain \(\alpha\).
Kjetil Halvorsen and Martin Maechler have an R function in their sfsmisc package that provides a fast approximation to the K-S critical values when \(\alpha=0.05\) (for 0.95 confidence bands). This function is reproduced below, and we use it to compute the 0.95-level simultaneous margins of error for the ECDF as a function of sample size.
This is a good opportunity to check the universal rule that the precision of an estimate is proportional to the square root of the sample size. The approxmoe function below multiplies the accurate margin of error at \(n=20\) by the square root of the ratio of 20 to the sample size of interest.
KSd <- function(n)
{
## `approx.ksD()'
## approximations for the critical level for Kolmogorov-Smirnov statistic D,
## for confidence level 0.95. Taken from Bickel & Doksum, table IX, p.483
## and Lienert G.A.(1975) who attributes to Miller,L.H.(1956), JASA
ifelse(n > 80,
1.358/( sqrt(n) + .12 + .11/sqrt(n)),## Bickel&Doksum, table IX,p.483
splinefun(c(1:9, 10, 15, 10 * 2:8),# from Lienert
c(.975, .84189, .70760, .62394, .56328,# 1:5
.51926, .48342, .45427, .43001, .40925,# 6:10
.33760, .29408, .24170, .21012,# 15,20,30,40
.18841, .17231, .15975, .14960)) (n))
}
plot(10 : 10000, KSd(10 : 10000), type='l', xlab='n',
ylab='ECDF Margin of Error')
abline(h=c(0.025, 0.05, 0.1), col=gray(0.6))
ns <- c(20, 50, 100, 180, 250, 500, 730, 750, 1000, 2935, 5000, 10000, 18400)
approxmoe <- function(n) 0.29408 * sqrt(20 / n)
data.frame(n=ns, MOE=round(KSd(ns), 3), MOEsqrt=round(approxmoe(ns), 3)) n MOE MOEsqrt
1 20 0.294 0.294
2 50 0.188 0.186
3 100 0.134 0.132
4 180 0.100 0.098
5 250 0.085 0.083
6 500 0.060 0.059
7 730 0.050 0.049
8 750 0.049 0.048
9 1000 0.043 0.042
10 2935 0.025 0.024
11 5000 0.019 0.019
12 10000 0.014 0.013
13 18400 0.010 0.010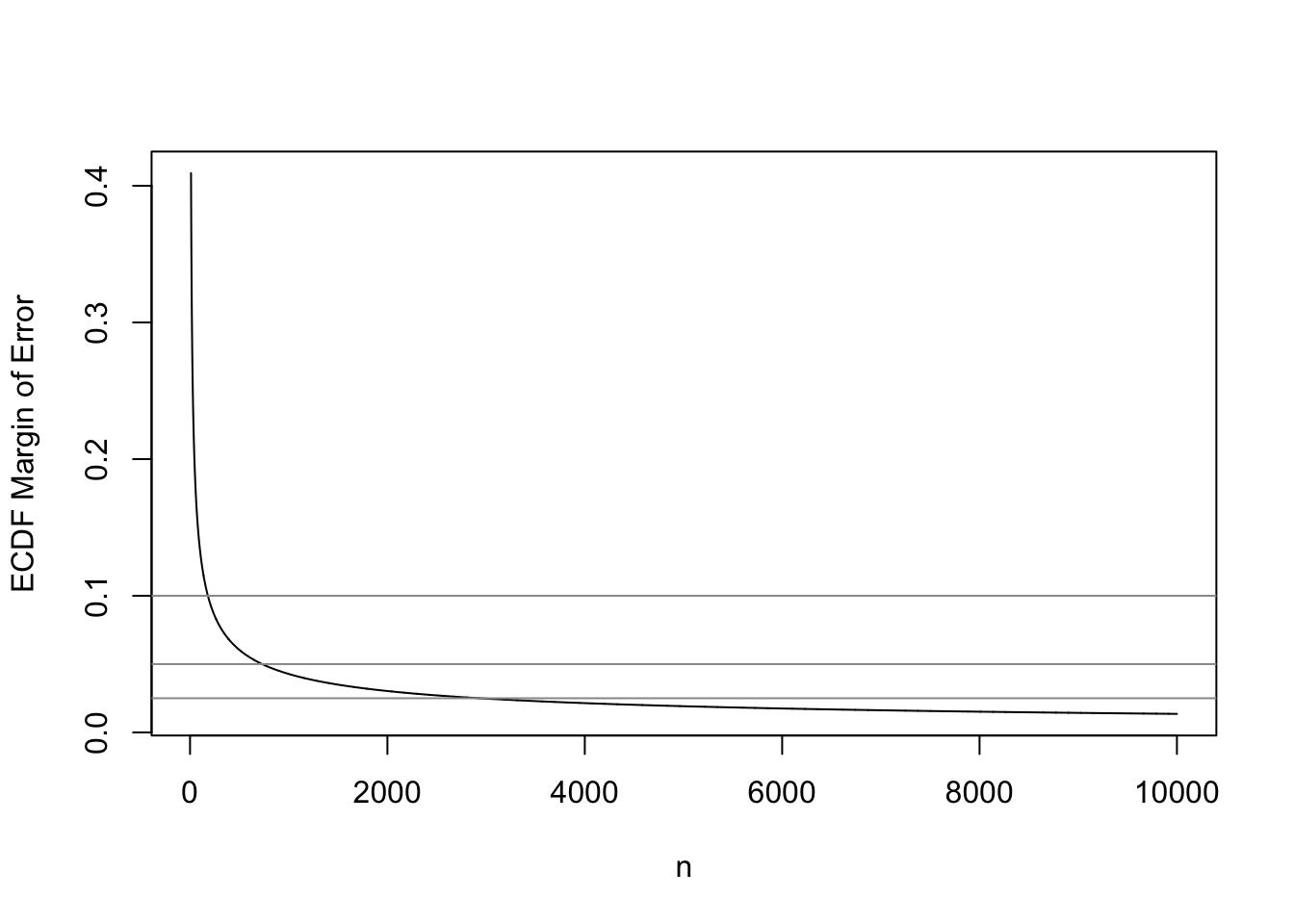
The sample size required to have a margin of error of \(\pm 0.01\) for the entire ECDF is 18,400. In other words if one desired to have a high degree of confidence that no estimated quantile will be off by more than a probability of 0.01, \(n=18,400\) will achieve this. For example, the sample 0.25 quantile (first quartile) may correspond to population quantiles 0.24-0.26. To achieve a \(\pm 0.1\) MOE requires \(n=180\), and to have \(\pm 0.05\) requires \(n=730\).
The “universal \(\sqrt{}\) rule” worked quite well. This will allow us to extend the calculations to any confidence level. The built-in R function qsmirnov allows us to compute exact critical values of the K-S test by computing the critical value of the Smirnov test when one of the two distributions it compares has an infinite sample size. Here \(n=10000\) is close enough to \(\infty\).
[1] 0.2943706[1] 0.29408[1] 0.2650735[1] 0.265 0.119 0.038```{r setup, include=FALSE}
require(Hmisc)
require(qreport)
hookaddcap() # make knitr call a function at the end of each chunk
# to try to automatically add to list of figure
options(prType='html')
getRs('qbookfun.r')
knitr::set_alias(w = 'fig.width', h = 'fig.height',
cap = 'fig.cap', scap ='fig.scap')
```
# Nonparametric Statistical Tests {#sec-nonpar}
`r mrg(bmovie(10), ddisc(10))`
## When to use non-parametric methods
* Short answer: Good default when $P$-values are needed and there are no covariates to adjust for
* Nonparametric methods are those not requiring one to assume a certain distribution for the raw data
+ In contrast, parametric methods assume data come from some underlying distribution
+ $t$-tests assume the data come form a Gaussian distribution
* Response variable ordinal or interval
* For ordinal responses nonparametric methods are preferred because they assume no spacing between categories
* No problem in using nonparametric tests on interval data
+ if normality holds, nonpar. test 0.95 efficient, i.e., has about the same power as the parametric test done on 0.95 of the observations^[The large-sample efficiency of the Wilcoxon and Spearman tests compared to $t$ and $r$ tests is $\frac{3}{\pi} = 0.9549$.]
+ if normality does not hold, nonpar. tests can be arbitrarily more efficient and powerful than the corresponding parametric test
+ an elegant and non-arbitrary way to deal with extreme values or outliers
+ rank-based nonparametric tests give the analyst freedom from having to choose the correct transformation of the measurement (as long as the optimum transformation is monotonic)
* Nonparametric methods are robust, many parametric methods are
not
+ Example: $t$-test comparing two sets of measurements
| Group 1 | Group 2 | Means | $P$ |
|:--------|:--------|:------|----:|
| 1 2 3 4 5 6 7 8 9 10 | 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 5.5 and 13.5 | 0.000019 |
| 1 2 3 4 5 6 7 8 9 10 | 7 8 9 10 11 12 13 14 15 16 17 18 19 20 **200**| 5.5 and **25.9** | 0.12 |
The SD is a particularly **non-robust** statistical estimator.
* Example: Fecal calprotectin being evaluated as a possible biomarker of disease severity (@fig-nonpar-calpro)
+ Calprotectin has an upper detection limit
+ Median can be calculated (mean cannot)
* If all you want is a $P$-value nonpar. tests are preferred
+ Especially if response is univariate and no need to adjust for covariates
* Pre-testing for normality and deciding nonparametric vs. parametric analysis is a bad idea
+ Tests for normality do not have a power of 1.0 and type I error of 0.0
+ Leads to temptation, e.g., an investigator might "forget" to do the test of normality if the $t$-test is significant
+ Doesn't acknowledge that nonparametric tests are very efficient even under normality
+ Pre-testing for normality alters the type I error and confidence interval coverage
* A drawback is that nonpar. tests do not correspond to usual confidence limits for effects
+ E.g., a CL for the difference in 2 means may include zero whereas the Wilcoxon test yields $P=0.01$
+ Point estimate that exactly corresponds to the Wilcoxon two-sample test is the Hodges-Lehman estimate of the location difference
- median of all possible differences between a measurement from group 1 and a measurement from group 2
* Nonparametric tests are often obtained by replacing the data with ranks across subjects and then doing the parametric test
* Many nonpar. tests give the same $P$-value regardless of how the data are transformed; a careful choice of transformation (e.g., log) must sometimes be used in the context of parametric tests
* $P$-values computed using e.g. the $t$ distribution are quite accurate for nonparametric tests
* In case of ties, midranks are used, e.g., if the raw data were 105 120 120 121 the ranks would be 1 2.5 2.5 4
| Parametric Test | Nonparametric Counterpart | Semiparametric Model Counterpart |
|:-----|:-----|:-----|
| 1-sample $t$ | Wilcoxon signed-rank | |
| 2-sample $t$ | Wilcoxon 2-sample rank-sum | Proportional odds |
| $k$-sample ANOVA | Kruskal-Wallis | Proportional odds |
| Pearson $r$ | Spearman $\rho$ | |
## One Sample Test: Wilcoxon Signed-Rank
* Almost always used on paired data where the column of values represents differences (e.g., post-pre) or log ratios
* The _sign test_ is the simplest test for the median difference being zero in the population
+ it just counts the number of positive differences after tossing out zero differences
+ tests $H_{0}:~$Prob$[x>0]=\frac{1}{2}$, i.e., that it is equally likely in the population to have a value below zero as it is to have a value above zero
+ as it ignores magnitudes completely, the test is inefficient
* By contrast, with the much more powerful Wilcoxon signed rank one-sample test, ranks of absolute differences are given the sign of the original difference
* Magnitudes of raw data matter more here than with the Wilcoxon 2-sample test
* Example: A crossover study in which the treatment order is randomized <br> Data arranged so that treatment A is in the first column, no matter which order treatment A was given
| A | B | B-A | Rank $|\mathrm{B-A}|$ | Signed Rank |
|-----|-----|-----:|-----:|-----:|
| 5 | 6 | 1 | 1.5 | 1.5 |
| 6 | 5 | -1 | 1.5 | -1.5 |
| 4 | 9 | 5 | 4.0 | 4.0 |
| 7 | 9 | 2 | 3.0 | 3.0 |
* A good approximation to an exact $P$-value may be obtained by computing
$$z = \frac{\sum{SR_{i}}}{\sqrt{\sum{SR_{i}^{2}}}},$$
where the signed rank for observation $i$ is $SR_{i}$. This formula
already takes ties into account without using Rosner's messy Eq.
9.5. We look up $|z|$ against the normal distribution. Here
$z=\frac{7}{\sqrt{29.5}}=1.29$ and and the 2-tailed $P$-value is given below.
```{r wsr}
sr <- c(1.5, -1.5, 4, 3)
z <- sum(sr) / sqrt(sum(sr ^ 2))
pval <- 2 * (1 - pnorm(abs(z)))
c(z=z, pval=pval)
```
* If all differences are positive or all are negative, the exact 2-tailed $P$-value is $\frac{1}{2^{n-1}}$
+ implies that $n$ must exceed 5 for any possibility of significance at the $\alpha=0.05$ level for a 2-tailed test
### One sample/Paired Test Example
* Sleep Dataset
+ Compare the effects of two soporific drugs.
+ Each subject receives placebo, Drug 1, and Drug 2
+ Study question: Is Drug 1 or Drug 2 more effective at increasing sleep?[Side comment: why did the investigators believe that the original 4-level ordinal outcome was so defective that it needed to be transformed in an information-losing way?]{.aside}
+ Dependent variable: Difference in hours of sleep comparing Drug 2 to Drug 1
+ $H_0:$ For any given subject, the difference in hours of sleep is equally likely to be positive or negative
+ See @sec-htest-sleeppaired for a parametric test on these data
+ Ignore the RD column for now
| Subject | Drug 1 | Drug 2 | Diff (2-1) | Sign | Rank | RD |
|-----:|-----:|-----:|-----:|-----:|-----:|-----:|
| 1 | 0.7| 1.9|1.2|+|3 | 5|
| 2 |-1.6| 0.8|2.4|+|8 |8.5|
| 3 |-0.2| 1.1|1.3|+|4.5 | 8|
| 4 |-1.2| 0.1|1.3|+|4.5 | 5|
| 5 |-0.1|-0.1|0.0|NA| | 0|
| 6 | 3.4| 4.4|1.0|+|2 | 2.5|
| 7 | 3.7| 5.5|1.8|+|7 | 3|
| 8 | 0.8| 1.6|0.8|+|1 | 2.5|
| 9 | 0.0| 4.6|4.6|+|9 | 13.0|
| 10 | 2.0| 3.4|1.4|+|6 | 1.5|
: Hours of extra sleep on drugs 1 and 2, differences, signs and signed ranks of sleep study data. Rank differences (RD) are also shown (@sec-nonpar-rd).
```{r wsrsleep}
drug1 <- c(.7, -1.6, -.2, -1.2, -.1, 3.4, 3.7, .8, 0, 2)
drug2 <- c(1.9, .8, 1.1, .1, -.1, 4.4, 5.5, 1.6, 4.6, 3.4)
wilcox.test(drug2, drug1, paired=TRUE)
wilcox.test(drug2 - drug1)
wilcox.test(drug2 - drug1, correct=FALSE)
sr <- c(3, 8, 4.5, 4.5, 0, 2, 7, 1, 9, 6)
z <- sum(sr) / sqrt(sum(sr ^ 2))
c(z=z, pval=2 * (1 - pnorm(abs(z))))
d <- data.frame(Drug=c(rep('Drug 1', 10), rep('Drug 2', 10),
rep('Difference', 10)),
extra=c(drug1, drug2, drug2 - drug1))
```
* Interpretation: Reject $H_0$, Drug 2 increases sleep by the same hours as Drug 1 ($p = 0.008$)
* Could also perform sign test on sleep data
+ If drugs are equally effective, should have same number of `+' and '-'
+ Observed data: 0 - 9 +, throw out 1 "no change"
+ Sign test (2-sided) $P$-value: Probability of observing 9 of 9 + or 9 of 9 -
+ $p = 0.004$, so evidence against $H_0$
```{r signtest}
2 * (1 / 2) ^ 9 # 2 * to make it two-tailed
```
* The signed rank test assumes that the distribution of differences is symmetric
* It tests whether the median difference is zero
* Also tests that the mean is zero
* In general it tests that, for two randomly chosen observations $i$ and $j$ with values (differences) $x_i$ and $x_j$, that the probability that $x_{i}+x_{j} > 0$ is $\frac{1}{2}$
* The estimator that corresponds exactly to the test in all situations is the pseudomedian, the median of all possible pairwise averages of $x_i$ and $x_j$, so one could say that the signed rank test tests $H_{0}$: pseudomedian=0
* The value $\frac{\overline{SR}}{n+1}-\frac{1}{2}$ estimates the probability that two randomly chosen observations have a positive sum, where $\overline{SR}$ is the mean of the column of signed ranks
* To test $H_{0}:\eta=\eta_{0}$, where $\eta$ is the population median (not a difference) and $\eta_{0}$ is some constant, we create the $n$ values $x_{i} - \eta_{0}$ and feed those to the signed rank test, assuming the distribution is symmetric
* When all nonzero values are of the same sign, the test reduces to the _sign test_ and the 2-tailed $P$-value is $(\frac{1}{2})^{n-1}$ where $n$ is the number of nonzero values
Test whether the continuity correction makes $P$-values closer to the
exact calculation^[The exact $P$-value is available only when there are no ties.}, and compare to our simple formula.]
```{r wsrcompare}
# Assume we are already starting with signed ranks as x
wsr <- function(x, ...) wilcox.test(x, ...)$p.value
sim <- function(x) {
z <- sum(x) / sqrt(sum(x ^ 2))
2 * (1 - pnorm(abs(z))) }
alls <- function(x) round(c(
continuity=wsr(x, correct=TRUE, exact=FALSE),
nocontinuity=wsr(x, correct=FALSE, exact=FALSE),
exact=wsr(x, exact=TRUE),
simple=sim(x)), 4)
alls(1:4)
alls(c(-1, 2 : 4))
alls(c(-2, c(1, 3, 4)))
alls(c(-1, -2, 3 : 5))
alls(c(-5, -1, 2, 3, 4, 6))
```
From these examples the guidance is to:
* Use the exact calculation if there are no ties
* Otherwise use the continuity correction (i.e., the default in `wilcox.test`) unlike the recommendation for the Pearson $\chi^2$ test
### Rank Difference Test {#sec-nonpar-rd}
Unlike the Wilcoxon two-sample comparison, the Wilcoxon signed-rank test has a significant disadvantage in depending on how the response varible is transformed. The rank difference test of @kor90ran^[Also available [here](https://www.researchgate.net/publication/230264296_The_rank_difference_test_A_new_and_meaningful_alternative_to_the_Wilcoxon_signed_ranks_test_for_ordinal_data)] solves this problem. Kornbrot's procedure is as follows
* Combine the $n$ "pre" and $n$ "post" observations into $2n$ observations
* Rank these values from 1 to $2n$ assigning midranks to ties in the usual Wilcoxon fashion
* Perform the Wilcoxon signed-rank test on the paired ranks
The test is implemented in the `R` [`rankdifferencetest`](https://cran.r-project.org/web/packages/rankdifferencetest) package by Brett Klamer^[The `rankdifferencetest` package will provide exact p-values in case of ties.] but the essence of the calculation is below where we run the rank difference test on the data analyzed previously. The rank differences RD are shown in the data table there.
```{r rdt}
m <- length(drug1)
ranks <- rank(c(drug1, drug2))
rank.diffs <- ranks[-(1 : m)] - ranks[1 : m]
wilcox.test(rank.diffs)
```
The results were identical to the signed-rank test because every subject had a higher drug 2 response than their drug 1 response except for the one that was tied which is excluded from both analyses.
## Two Sample Test: Wilcoxon--Mann--Whitney
* The Wilcoxon--Mann--Whitney (WMW) 2-sample rank sum test is for testing for equality of central tendency of two distributions (for unpaired data)
* Ranking is done by combining the two samples and ignoring which sample each observation came from
* Example:
| | | | | |
|:------------------|----:|----:|----:|-----:|
| Females | 120 | 118 | 121 | 119 |
| Males | 124 | 120 | 133 | |
| Ranks for Females | 3.5 | 1 | 5 | 2 |
| Ranks for Males | 6 | 3.5 | 7 | |
* Doing a 2-sample $t$-test using these ranks as if they were raw data and computing the $P$-value against 4+3-2=5 d.f. will work quite well
* Some statistical packages compute $P$-values exactly (especially if there are no ties)
* Loosely speaking the WMW test tests whether the population medians of the two groups are the same
* More accurately and more generally, it tests whether observations in one population tend to be larger than observations in the other
* Letting $x_1$ and $x_2$ respectively be randomly chosen observations from populations one and two, WMW tests $H_{0}:c=\frac{1}{2}$, where $c=$Prob$[x_{1} > x_{2}]$
* The $c$ index (_concordance probability_) may be estimated by computing
$$c = \frac{\bar{R}-\frac{n_{1}+1}{2}}{n_{2}},$$
where $\bar{R}$ is the mean of the ranks in group 1; <br> For the above data $\bar{R} = 2.875$ and $c=\frac{2.875-2.5}{3}=0.125$, so we estimate that the probability is 0.125 that a randomly chosen female has a value greater than a randomly chosen male.
* In diagnostic studies where $x$ is the continuous result of a medical test and the grouping variable is diseased vs. non-diseased, $c$ is the area under the receiver operating characteristic (ROC) curve
* Test still has the "probability of ordering" interpretation when the variances of the two samples are markedly different, but it no longer tests anything like the difference in population medians
If there is no overlap between measurements from group 1 and those from group 2, the exact 2-sided $P$-value for the Wilcoxon test is $2/ \frac{n!}{n_{1}! n_{2}!}$. If $n_{1}=n_{2}$, $n_{1}$ must be $\geq 4$ to obtain $P < 0.05$ (in this case $P = 0.029$).
<!-- Thanks: Rameela and Bill--->
<!-- If R1 denotes the rank sum of the group with sample size m, then the--->
<!-- smallest possible value of R1 is the sum of the m smallest ranks 1 + 2 +--->
<!-- ... m = m*(m+1)/2. The probability of this value is 1/[(m+n)Cm] -- C--->
<!-- implies choose.--->
### Two Sample WMW example {#sec-calprotectin}
* Fecal calprotectin being evaluated as a possible biomarker of disease severity
* Calprotectin measured in 26 subjects, 8 observed to have no/mild activity by endoscopy
* Calprotectin has upper detection limit at 2500 units
+ A type of missing data, but need to keep in analysis
* Study question: Are calprotectin levels different in subjects with no or mild activity compared to subjects with moderate or severe activity?
* Statement of the null hypothesis
+ $H_0:$ Populations with no/mild activity have the same distribution of calprotectin as populations with moderate/severe activity
+ $H_0: c = \frac{1}{2}$
```{r calpro,w=6,h=3,cap='Fecal calprotectin by endoscopy severity rating. Red dotted line is the detection limit. Ordinal disease categories should not have been combined.',scap='Fecal calprotectin by severity'}
#| label: fig-nonpar-calpro
#Fecal Calprotectin: 2500 is above detection limit
calpro <- c(2500, 244, 2500, 726, 86, 2500, 61, 392, 2500, 114, 1226,
2500, 168, 910, 627, 2500, 781, 57, 483, 30, 925, 1027,
2500, 2500, 38, 18)
# Endoscopy score: 1 = No/Mild, 2=Mod/Severe Disease
# Would have been far better to code dose as 4 ordinal levels
endo <- c(2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 2,
2, 2, 2, 2, 2, 1, 1)
endo <- factor(endo, 1 : 2,
c("No or Mild Activity", "Moderate or Severe Activity"))
require(ggplot2)
ggplot(data.frame(endo, calpro), aes(y=calpro, x=endo)) +
geom_boxplot(color='lightblue', alpha=.85, width=.4) +
geom_dotplot(binaxis='y', stackdir='center', position='dodge') +
xlab('') + ylab('Fecal Calprotectin') + coord_flip() +
geom_hline(aes(yintercept=2500, col=I('red')), linetype='dotted')
wilcox.test(calpro ~ endo)
```
<!-- See http://docs.ggplot2.org/0.9.3/geom_dotplot.html--->
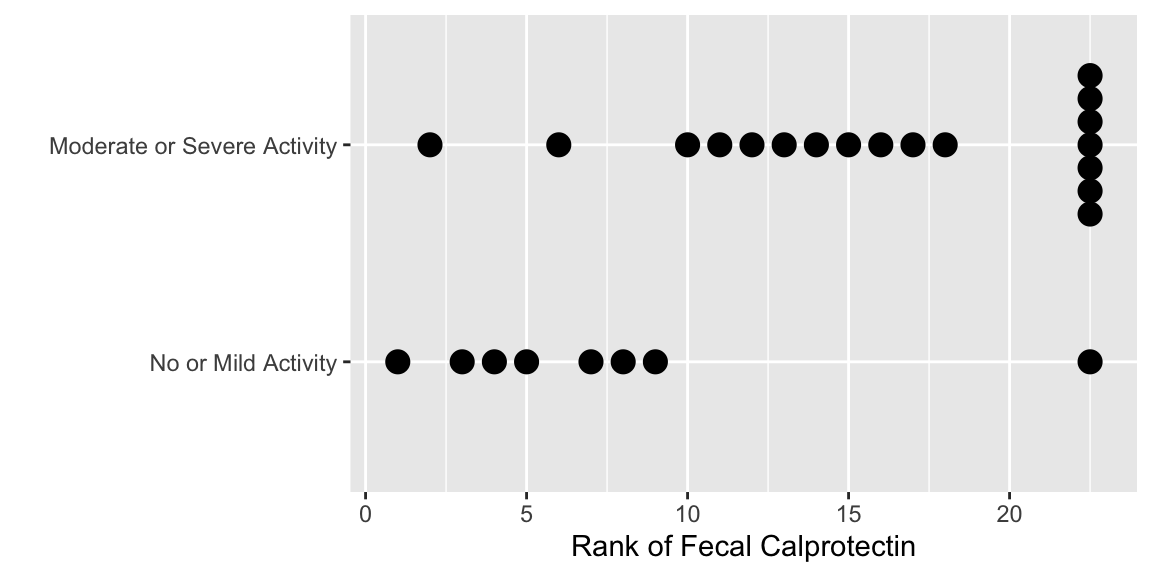
The following plots the ranks that are used in the
Wilcoxon-Mann-Whitney two-sample rank sum test.
```{r calpror,w=6,h=3,cap='Ranks of calprotectin'}
#| label: fig-nonpar-calpror
ggplot(data.frame(endo, calpro), aes(y=rank(calpro), x=endo)) +
geom_dotplot(binaxis='y', stackdir='center', position='dodge') +
xlab('') + ylab('Rank of Fecal Calprotectin') + coord_flip()
```
* Test statistic $W$ equals the sum of the ranks in the no/mild group minus $n_1 \times (n_1 + 1) / 2$, where $n_1$ is the number of subjects in then no/mild sample
* $W = 59.5 - \frac{8\times 9}{2} = 23.5$
* A common (but loose) interpretation: People with moderate/severe activity have higher _median_ fecal calprotectin levels than people with no/mild activity ($p = 0.007$).
* Better: remove _median_ and supplement with the $c$-index (concordance probability) or Somers' $D_{xy}$ rank correlation between calprotectin and endoscopy status. The code for the `R` `somers2` function shows how the concordance probability is computed from the mean of the ranks in one of the two groups.
```{r cendo}
require(Hmisc)
# Convert endo to a binary variable
somers2(calpro, endo=='Moderate or Severe Activity')
```
If you type `somers2` to list the code for the function you will
see that the $c$-index is tightly related to the Wilcoxon test when
you see this code:
```{r ccode,eval=FALSE}
mean.rank <- mean(rank(x)[y == 1])
c.index <- (mean.rank - (n1 + 1)/2) / (n - n1)
```
### Point and Interval Estimates for Wilcoxon Two-Sample Comparison {#sec-nonpar-mf}
As mentioned earlier, the effect estimate that is exactly consistent
with the Wilcoxon two-sample test is the robust Hodges-Lehman estimator---the
median of all possible differences between a measurement from group 1
and a measurement from group 2. There is a confidence interval for
this estimator.
* Assume data come from distributions with same shape and differ only in location
* Consider a sample of 4 males and 3 females
* Difference in sample medians is 124 - 119.5 = 4.5
* Consider all possible differences between sample 1 and sample 2
| | Female $\rightarrow$ | | | |
|:-----|-----:|---:|----:|----:|
| Male $\downarrow$ | 120 | 118 | 121 | 119 |
| 124 | 4 | 6 | 3 | 5 |
| 120 | 0 | 2 | -1 | 1 |
| 133 | 13 | 15 | 12 | 14 |
* Hodges-Lehman estimate of the sex effect: median of the 12 differences = 4.5
* In this case equaled difference in sample medians just by coincidence
```{r hlest}
female <- c(120, 118, 121, 119)
male <- c(124, 120, 133)
differences <- outer(male, female, '-')
differences
median(differences)
# Can't figure out how difference in location is computed below
# It's not the Hodges-Lehman estimate
wilcox.test(male, female, conf.int=TRUE)
```
In general, $1 - \alpha$ confidence intervals are the set of values that if
hypothesized to be the true location parameter would not be rejected
at the $\alpha$ level. `wilcox.test` computes the location shift
by solving for the hypothesized value that yields $P=1.0$ instead of
the more proper median of all differences. Look into this further by
plotting the $P$-value as a function of the hypothesized value.
```{r checkhl,cap='Wilcoxon $P$-value vs. hypothesized male-female difference. Horizontal line is $P=0.05$. Vertical lines from left to right are the lower 0.95 confidence limit from `wilcox.test`, the median difference, the Hodges-Lehman estimator as computed by `wilcox.test`, and the upper 0.95 confidence limit from `wilcox.test`.',scap='Wilcoxon $P$-value vs. hypothesized difference.'}
#| label: fig-nonpar-checkhl
#| fig-height: 3.5
#| fig-width: 4.25
dif <- seq(-3, 15, by=.1)
n <- length(dif)
pval <- numeric(n)
for(i in 1 : n) pval[i] <- wilcox.test(male - dif[i], female)$p.value
ggplot(data.frame(dif, pval), aes(x=dif, y=pval)) +
geom_step() +
geom_hline(yintercept=.05, col='red', linetype='dotted') +
geom_vline(xintercept=c(4.5, 4.791, -1, 15), col='red', linetype='dotted') +
xlab('Difference') + ylab('P-value')
```
See @sec-nonpar-clmed for a more approximate confidence interval.
## Confidence Intervals for Medians and Their Differences {#sec-nonpar-clmed}
* Confidence intervals for the median (one sample)
+ Table 18.4 (Altman) gives the ranks of the observations to be used to give approximate confidence intervals for the median
+ e.g., if $n = 12$, the $3^\mathrm{rd}$ and $10^\mathrm{th}$ largest values give a $0.961$ confidence interval
+ For larger sample sizes, the lower ranked value ($r$) and upper ranked value ($s$) to select for an approximate $0.95$ confidence interval for the population median is
$$r = \frac{n}{2} - 1.96*\frac{\sqrt{n}}{2} ~~~\mathrm{and}~~~ s = 1 + \frac{n}{2} + 1.96*\frac{\sqrt{n}}{2}$$
*
+ e.g., if $n = 100$ then $r = 40.2$ and $s = 60.8$, so we would pick the $40^\mathrm{th}$ and $61^\mathrm{st}$ largest values from the sample to specify a $0.95$ confidence interval for the population median
+ For exact confidence interval for the median see<br> [stats.stackexchange.com/questions/186957](https://stats.stackexchange.com/questions/186957), which also discusses why there is no exact nonparametric confidence interval for the mean. Let's get the exact order statistics that result in an exact confidence interval for the median:
```{r medciexact}
# Exact CI for median from DescTools package SignTest.default
# See also ttp://www.stat.umn.edu/geyer/old03/5102/notes/rank.pdf,
# http://de.scribd.com/doc/75941305/Confidence-Interval-for-Median-Based-on-Sign-Test
cimed <- function(x, alpha=0.05, na.rm=FALSE) {
if(na.rm) x <- x[! is.na(x)]
n <- length(x)
k <- qbinom(p=alpha / 2, size=n, prob=0.5, lower.tail=TRUE)
## Actual CL: 1 - 2 * pbinom(k - 1, size=n, prob=0.5) >= 1 - alpha
sort(x)[c(k, n - k + 1)]
}
cimed(1 : 100)
```
For $n=100$ we see that the approximate interval happened to be exact.
* Confidence intervals for the difference in two medians (two samples)
+ We don't have a nonparametric interval for this
+ Instead get Hodges-Lehman estimate
+ Assume data come from distributions with same shape and differ only in location
+ Considers all possible differences between sample 1 and sample 2 using male-female data in @sec-nonpar-mf
+ An estimate of the median difference (males - females) is the median of these 12 differences, with the $3^\mathrm{rd}$ and $10^\mathrm{th}$ largest values giving an (approximate) 0.95 CI
+ Median estimate = 4.5, 0.95 CI = [1, 13]
+ Specific formulas found in Altman, pages 40-41
* Bootstrap
+ General method, not just for medians
+ Non-parametric, does not assume symmetry (but may not be accurate)
+ Iterative method that repeatedly samples from the original data
+ Algorithm for creating a $0.95$ CI for the difference in two medians
1. Sample _with replacement_ from sample 1 and sample 2
1. Calculate the difference in medians, save result
1. Repeat Steps 1 and 2 1000 times
+ A (naive) $0.95$ CI is given by the $25^\mathrm{th}$ and $975^\mathrm{th}$ largest values of your $1000$ median differences
+ For the male/female data, median estimate = 4.5, 0.95 CI = [-0.5, 14.5], which agrees with the conclusion from a WMW rank sum test ($p = 0.15$). Note that the more accurate CI for the Hodges-Lehman estimate of $[-1, 15]$ was given earlier (output of `wilcox.test`).
```{r diffmedboot}
#| label: fig-nonpar-diffmedboot
#| fig-cap: "Bootstrapped differences in medians"
diffs <- numeric(1000)
set.seed(13)
for(i in 1 : 1000) diffs[i] <-
median(sample(male, replace=TRUE)) - median(sample(female, replace=TRUE))
ggplot(data.frame(diffs), aes(x=diffs)) + xlab('Differences in Medians') +
geom_histogram(bin_widith=.01, color='blue', fill='white')
quantile(diffs, c(0.025, 0.975))
```
But recall that the Wilcoxon test does not really test the difference
in medians but rather the median of all differences.
## Strategy
* Don't assess normality of data
* Use nonparametric test in any case, to get $P$-values
* Use nonparametric confidence intervals for means and medians^[A good nonparametric confidence for a population mean that does not even assume a symmetric distribution can be obtained from the bootstrap simulation procedure.] which will be more in conformance to what the nonpar. test is testing
* To obtain nonparametric confidence limits for means and differences in means, the bootstrap percentile method may easily be used and it does not assume symmetry of the data distribution
## Generalization of the Wilcoxon/Kruskal-Wallis Test
`r mrg(bmovie(11), ddisc(11))`
* Proportional odds (PO) ordinal logistic model
* Contains Wilcoxon 2-sample and Kruskal-Wallis tests as special cases
+ numerator of the score test for the PO model, when there is only the grouping variable in the model, is exactly the Wilcoxon statistic
* Special case of PO model is the ordinary binary logistic model
* Advantages over nonparametric tests:
+ can adjust for covariates
+ more accurate $P$-values even with extreme number of tied values
+ provides a framework for consistent pairwise comparisons^[When using the Kruskal-Wallis test followed by pairwise Wilcoxon tests, these pairwise tests can be inconsistent with each other, because they re-rank the data based only on two groups, destroying the transitivity property, e.g. treatment A can be better than B which is better than C but C is better than A.]
+ provides estimates of means, quantiles, and exceedance probabilities
+ sets the stage for a Bayesian PO model, so can get a Bayesian Wilcoxon test
* Other ordinal response models are available, e.g., Cox proportional hazards model
* These models are _semiparametric models_
+ parametric in additivity and linearity (by default) assumptions
+ nonparametric in not assuming a distribution for the response variable
* Like nonparametric tests, $P$-values are unaffected by monotonic transformations of $Y$
* If the response variable $Y$ has $k$ distinct values $y_1, y_2, \dots, y_k$ in the sample, semiparametric models have $k-1$ intercepts
* Binary logistic model deals with prob. of only one event ($Y=1$ vs. $Y=0$)
* For ordinal $Y$ there are $k-1$ events
* Model these as cumulative probabilities to make use of ordering of $Y$ values
* Model: $P(Y \geq y | X) = \frac{1}{1 + \exp[-(\alpha_y + \beta_1 x_1 + \beta_2 x_2 + \dots)]}$
* $\alpha_y$ is the $j^{\mathrm{th}}$ intercept when $y = y_{j+1}$, e.g. the first intercept corresponds to the second lowest distinct $Y$ value $y_2$
* Special case: 2-group problem: $P(Y \geq y | \mathrm{group}) = \frac{1}{1 + \exp[-(\alpha_y + \beta_1[\mathrm{group B}])]}$
+ $\exp(\beta_1)$ is the ratio of odds that $Y \geq y$ in group B vs. $Y \geq y$ in group A, for all $y > y_1$
+ as before $[x]$ is the 0-1 indicator variable for $x$ being true
+ $\beta_1 > 0 \rightarrow Y$ values higher in group B
+ $k=2 \rightarrow$ model is the binary logistic model (where we take $\alpha_1 = \beta_0$)
* These intercepts $\alpha_1, \alpha_2, \dots, \alpha_{k-1}$ encode the entire empirical distribution of $Y$ for one of the groups
+ $\rightarrow$ the model assumes nothing about the $Y$ distribution
+ it only assumes how the distribution of $Y$ for one type of subject is connected to the distribution for another type of subject
+ PO model for a two-group problem assumes that the logit of the two cumulative distribution functions are parallel
+ if PO doesn't hold, PO model may still be better than alternatives
+ PO is also what the Wilcoxon/Kruskal-Wallis test assumes to have optimal power
+ don't need an $\alpha$ for the lowest observed $Y$ value since $P(Y \geq ~\mathrm{minimum } Y) = 1$
* `R` `rms` package `orm` function fits the PO model^[`orm` also fits other models using link functions other than the logit.] and is especially made for continuous $Y$, with fast run times for up to 6000 intercepts
### Kruskal-Wallis Test
* Notice we haven't described rank ANOVA---the Kruskal-Wallis test
* Don't need it; just form a PO model with more than one indicator variable
* E.g., to test for any differences among four groups A B C D form 3 indicator variables for B C D and let A be the reference cell that corresponds to the $\alpha$ intercepts
+ model is logit$P(Y \geq y | \mathrm{group}) = \alpha_y + \beta_1 [B] + \beta_2 [C] + \beta_3 [D]$
* Use the likelihood ratio $\chi^2$ test from this model to test the global null hypothesis A=B=C=D with 3 d.f.
* Can obtain consistent pairwise comparisons by forming odds ratios for any comparison
+ e.g. C:A comparison will use $\exp(\hat{\beta_{2}})$
+ C:B comparison OR: $\exp(\hat{\beta_{2}} - \hat{\beta_{1}})$
* As before can convert the ORs to differences in medians/means because unlike the original nonparametric tests, the PO model can be used to obtain many types of predictions^[The predicted mean for a set of covariate settings is obtained by using all the intercepts and $\beta$s to get exceedance probabilities for $Y \geq y$, taking successive differences in those probabilities to get cell probabilities that $Y=y$, then multiplying cell probabilities by the $y$ value attached to them, and summing. This is the formula for the mean for a discrete distribution.]
* Illustrate this by a non-PO example, checking to see how well the PO model can recover the sample means when assuming (the slightly incorrect) PO
* Take 4 samples from normal distributions with the same variances but different means
* Also show how to compare two of the samples without re-ranking the data as inconsistent Wilcoxon tests would do
```{r orm4}
set.seed(1)
group <- rep(c('A','B','C','D'), 100)
y <- rnorm(400, 100, 15) + 10*(group == 'B') + 20*(group=='C') + 30*(group=='D')
require(rms)
options(prType='html')
dd <- datadist(group, y); options(datadist='dd')
f <- orm(y ~ group)
f # use LR chi-square test as replacement for Kruskal-Wallis
# Derive R function to use all intercepts and betas to compute predicted means
M <- Mean(f)
Predict(f, group, fun=M)
# Compare with sample means
summarize(y, group, smean.cl.normal)
# Compare B and C
k <- contrast(f, list(group='C'), list(group='B'))
k
# Show odds ratios instead of differences in betas
print(k, fun=exp)
```
### PO Re-analysis
* Reconsider the calprotectin data analyzed in @sec-calprotectin
* Wilcoxon: $P=0.0068, c=0.837$
* Frequentist PO model:
<small>
```{r po}
require(rms)
options(prType='html')
dd <- datadist(calpro, endo); options(datadist='dd')
f <- orm(calpro ~ endo)
print(f, intercepts=TRUE)
```
</small>
* Intercept -3.1166 corresponds $Y$ being at or above the upper detection limit
* Use the likelihood ratio (LR) $\chi^2$ test from the model
* To estimate an exceedance probability just select the corresponding intercept and compute as for a binary logistic model
* The 18 intercepts for 19 distinct $Y$ values represent the logit of the empirical cumulative distribution function for the no/mild reference group if the two groups are in proportional odds^[The intercepts really represent the logit of one minus the CDF, moved one $Y$ value.]. Add 2.7586 to those intercepts to get the logit CDF for the moderate/severe group.
* Compute odds ratio and CI
<small>
```{r poor,results='asis'}
summary(f, endo='No or Mild Activity')
```
</small>
* The above odds ratio of 15.8 is the odds of having calprotectin $\geq y$ in the moderate/severe activity group vs. the no/mild activity group
+ By the PO assumption this odds ratio is the same for all $y$
* Simulations provided an empirical conversion of the PO regression coefficient to $c$:
```{r approxc}
b <- coef(f)['endo=Moderate or Severe Activity']
cindex <- plogis((b - 0.0029) / 1.5405)
cindex
```
Compare this to the exact value of 0.837.
* From the fitted PO model obtain for each group, compute along with sample estimates:
+ prob. calprotectin at or above the upper limit of normal
+ mean
+ median
* In the output of `Predict()` see the point estimates under `yhat`, starting with the estimates for $P(Y \geq 2500)$, i.e., marker value at or above the upper detection limit
```{r poderived}
ex <- ExProb(f)
exceed <- function(lp) ex(lp, y=2500)
ymean <- Mean(f)
yquant <- Quantile(f)
ymed <- function(lp) yquant(0.5, lp=lp)
Predict(f, endo, fun=exceed)
# Compute empirical exceedance probabilities
tapply(calpro >= 2500, endo, mean)
# Note that imposing PO assumption made modeled means closer together than
# stratified sample means
Predict(f, endo, fun=ymean)
tapply(calpro, endo, mean)
Predict(f, endo, fun=ymed)
tapply(calpro, endo, median)
```
* Note: confidence intervals for these derived quantities are approximate
* Compute estimated median for every subject
* As a measure of predictive strength compute the mean absolute difference between predicted median and observed raw values
* Compare this to the mean absolute difference between a constant prediction (the overall median) and predicted medians
```{r}
pmed <- ymed(predict(f))
mean(abs(calpro - pmed))
mean(abs(calpro - median(calpro)))
```
* Repeat with a Bayesian fit, using posterior mean regression coefficients to estimate covariate-specific medians
* A better but slightly more involved approach would be to compute covariate-specific medians for all posterior draws of $\hat{\beta}$.
```{r}
require(rmsb)
options(mc.cores = parallel::detectCores() - 1,
rmsb.backend='cmdstan') # use max # CPUs
cmdstanr::set_cmdstan_path(cmdstan.loc)
b <- blrm(calpro ~ endo)
b
yquantb <- Quantile(b)
ymedb <- function(lp) yquantb(0.5, lp=lp)
pmedb <- ymedb(predict(b, cint=0))
cbind(pmed, pmedb)
mean(abs(calpro - pmedb))
```
## Checking Assumptions of the Wilcoxon Test
* Proportional odds (PO) model and its special case the Wilcoxon test assume PO
* What does it mean to _assume_ PO?
+ Under $H_0$: the two distributions are **identical** there is no assumption, i.e., type I error probability will behave as advertised
+ Under $H_1$ the test may still work OK but it will not be _optimal_ unless PO holds
* To check PO:
+ Compute the empirical cumulative distribution function (ECDF) for the response variable, stratified by group (see @sec-desc-dist)
+ Take the logit transformation of each ECDF
+ Check for parallelism
+ Linearity would be required **only** if using a parametric logistic distribution instead of using our semiparametric PO model
* Parametric $t$-test requires parallelism **and** linearity when the ECDFs are normal-inverse transformed
+ linearity: normal distribution (like q-q plot)
+ parallelism: equal variances
* Problem with assumption checking is that with small samples ECDFs are too noisy to see patterns clearly
* Example from a larger dataset: Mayo Clinic Primary Biliary Cirrhosis Dataset
* Compare distribution of serum bilirubin for those patients with spider veins vs. those without
```{r pbc}
#| label: fig-nonpar-pbc
#| fig-cap: "Checking for parallelism on the logit scale (proportional odds Wilcoxon assumption)"
#| fig-scap: "Checking Wilcoxon assumption"
#| fig-height: 3.5
#| fig-width: 4.25
getHdata(pbc)
# Take logit of ECDF
Ecdf(~ bili, group = spiders, data=pbc, fun=qlogis)
```
* The curves are primarily parallel (even at the far left, despite the optical illusion)
* Nonlinearity is irrelevant
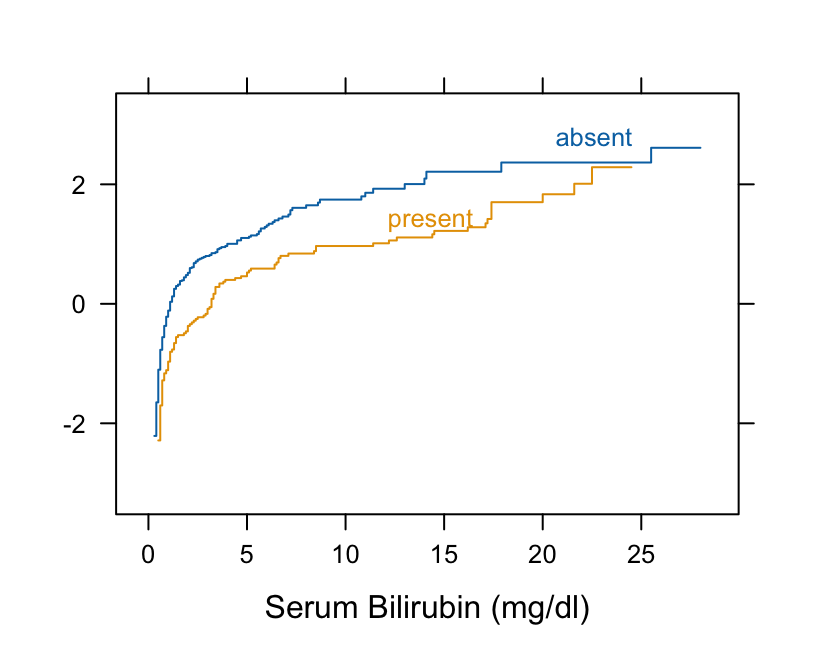
* Check $t$-test assumptions
```{r pbc2}
#| label: fig-nonpar-pbc2
#| fig-cap: "Checking for parallelism on the normal inverse scale (equal variance $t$-test and normal scores rank test assumptions)"
#| fig-scap: "Checking $t$-test assumption"
#| fig-height: 3.5
#| fig-width: 4.25
Ecdf(~ bili, group=spiders, data=pbc, fun=qnorm)
```
* Curves are primarily parallel (variances are equal; probit ordinal regression or normal scores rank test would work)
* **But** they are not straight lines as required by $t$-test normality assumption
## Two-Way ANOVA Ordinal Regression Example {#sec-nonpar-2way}
* Problem and data posted to [stats.stackexchange.com/questions/622230](https://stats.stackexchange.com/questions/622230)
* Two binary factors: sex and surface (for dorsal/ventral)
* Response variable: y
* There is significant uncertainty in how to transform y for a parametric analysis
* Ordinal models provide the same regression coefficients, standard errors, and confidence intervals regardless of how y is transformed (as long as the transformation is monotonic, e.g., log, square root, etc.)
* Quantiles are also unaffected by any choice of transformation
* Estimates means do depend on the transformation used
* Ordinal models are also robust to "outliers"
```{r}
d <- csv.get(textConnection('
id sex surface y
1 female UN 1255
2 female UN 542
3 female UN 818
1 female UN 274
2 female UN 261
3 female UN 314
1 female UP 552
2 female UP 548
3 female UP 721
1 female UP 431
2 female UP 354
3 female UP 738
4 male UN 901
5 male UN 619
6 male UN 861
7 male UN 713
8 male UN 717
4 male UN 275
5 male UN 300
6 male UN 244
7 male UN 281
8 male UN 231
4 male UP 532
5 male UP 451
6 male UP 482
7 male UP 374
8 male UP 424
4 male UP 193
5 male UP 118
6 male UP 207
7 male UP 208
8 male UP 252
'), sep='\t') #<1>
require(data.table)
setDT(d) #<2>
```
1. `\t` is the tab character
2. turn the `data.frame` into a `data.table`
* Tentatively choose the proportional odds (PO) model
* Check its assumptions (note this is difficult with small $N$)
* Stratify by both factors so there are 4 groups
* Check the logit link (PO assumption) by taking the logit of the stratified empirical cumulative distribution function (CDF) estimates
+ Can't take logit of 1.0 so for those values substitute 0.99
* PO assumption $\equiv$ parallelism of logit-transformed cumulative distributions
* PO assumption is analogous to equal variance assumption in ANOVA
* Unlike ANOVA there is no assumption about the shape of any one group's CDF
```{r}
#| label: fig-nonpar-2way-checkpo
#| fig-cap: "logit ECDF plots for checking the PO assumption (parallelism) in the 2-factor problem"
#| fig-height: 4.75
#| fig-width: 5.75
v <- d[, ecdfSteps(y, extend=FALSE), by=.(sex, surface)] #<1>
ggplot(v, aes(x, qlogis(pmin(y, 0.99)), color=sex, linetype=surface)) +
geom_step() + xlab('y') + ylab('logit ECDF')
```
1. `ecdfSteps` is in the `Hmisc` package; it computes coordinates of empirical cumulative distribution functions; `data.table` uses `by=` for stratification
* Parallelism is hard to check with $N=32$ stratified into 4 groups, but no blatant violations are obvious
* Fit a proportional odds model without interaction, as the sample size does not allow one to adequately estimate the interaction effect
* Use likelihood ratio $\chi^2$ statistics, which are more accurate than the usual Wald statistics
```{r}
dd <- datadist(d); options(datadist='dd') #<1>
f <- orm(y ~ sex + surface, data=d, x=TRUE, y=TRUE) #<2>
print(f, intercepts=TRUE) #<3>
anova(f, test='LR')
```
1. Save data distribution summaries
2. `orm` is the `rms` package's function for analyzing continuous responses as ordinal. It also works for discrete Y but the `rms` `lrm` function is sometimes better for that. `x=TRUE, y=TRUE` is for getting likelihood ratio $\chi^2$ tests.
3. The default is not to print the intercepts if there are more than 10 of them
* Note that the intercepts encode the (logits of) one minus the empirical distribution function for the reference group (female UN) [This is why no distribution is assumed for any one covariate setting.]{.aside}
* One adjusted $R^2$ is duplicated because the actual sample size (32) equals the effective sample size due to there being no ties in y
* There is a small amount of evidence ($p=0.097$) that either of the two factors is associated with `y`
* There is very little evidence for an association with surface
* There is a small amount of evidence for a sex "effect"
* The low $R_\text{adj}^{2}$ of 0.08 implies that the model is of limited use for estimation / prediction
* Estimate means and medians for all 4 combinations of factors, using the model and empirically
```{r}
M <- Mean(f) #<1>
qu <- Quantile(f) #<2>
med <- function(lp) qu(0.5, lp) #<3>
g <- function(x) list(Mean=mean(x), Median=median(x))
cat('Sample estimates\n')
d[, g(y), by=.(sex, surface)]
cat('\nModel estimates of means (yhat)\n')
Predict(f, surface, sex=.q(female, male), fun=M) #<4>
cat('\nModel estimates of medians (yhat)\n')
Predict(f, surface, sex=.q(female, male), fun=med)
```
1. Derives an R function that translates from logit scale to mean
2. Likewise for quantiles
3. Particular case of quantiles: median
4. `fun=...` causes predicted log odds to be transformed by the named function; `.q` is an R `Hmisc` package function that quotes strings for you
* Note that empirical stratified sample estimates of means and medians do not assume PO and do not assume the absence of an interaction, but they have low precision due to dividing the sample size by 4
* Model estimates assume no interaction and effectively divide the sample size by 3
## Regression Analysis of Paired Data {#sec-nonpar-pairmodel}
Just as a [binary logistic model may be used to do the McNemar test](https://stats.stackexchange.com/questions/560142) for paired binary data, [regression can be used](https://medium.com/@marco_laube/the-paired-t-test-and-linear-mixed-models-185a084d7813) for testing for effects in paired ordinal or continuous data. Regression is more general:
* Can adjust for covariates
* Can have more than 2 (pre, post) periods, e.g., handles a multi-period crossover study
* Paired $t$-test is equivalent to
+ linear regression blocking on subject (subjects are fixed effects)
+ mixed effects linear model with random intercepts for subjects
* Rank difference test is similar to
+ PO model blocking on subject (but there problems with having too many parameters)
+ mixed effects PO model
Let's illustrate this by re-analyzing paired data analyzed previously.
```{r}
w <- t.test(drug1, drug2, paired=TRUE)
w
w$stderr # fetch standard error of mean difference
y <- c(drug1, drug2)
drug <- rep(c('A', 'B'), each=length(drug1))
id <- factor(rep(1 : length(drug1), 2))
d <- data.frame(drug, y, id)
dd <- datadist(d); options(datadist='dd')
ols(y ~ drug + id)
```
* Ignore overall $\chi^2$ test
* $\hat{\beta}$ equals the difference computed by the paired $t$-test
* S.E. is also identical
* Now run random intercepts model
```{r}
require(nlme)
summary(lme(y ~ drug, random = ~ 1 | id, data=d))
```
* Try a regular regression model where intra-person correlation is adjusted for using the cluster sandwich covariance estimator
```{r}
f <- ols(y ~ drug, x=TRUE, y=TRUE) #<1>
robcov(f, id)
```
1. `x=TRUE, y=TRUE` needed for `robcov`, which is in the `rms` package
* Standard error is a bit too small
* P-value is too small because the sandwich estimator leads to a $z$-statistic and we should probably be using a $t$-statistic with the usual d.f.
* Now compare rank difference test with PO model
```{r}
f <- orm(y ~ drug + id, x=TRUE, y=TRUE)
anova(f, test='LR')
```
* $\chi^2$ for treatment (drug) is a bit larger than expected
* Try mixed PO model with normal random effects for subjects
* This did not converge and resulted in unrealistically large test statistic
```{r}
require(ordinal)
f <- clmm2(factor(y) ~ drug, random = id, data=d, link='logistic', Hess=TRUE)
summary(f)
```
`clmm2` uses a Laplace approximation for numerical integration. Let's try using 7-point quadrature integration instead.
```{r}
f <- clmm2(factor(y) ~ drug, random = id, data=d, link='logistic', Hess=TRUE,
nAGQ=7)
summary(f)
```
* This frequentist mixed model fit seems to be fine
* A Bayesian mixed effects PO model did not have any trouble
* Mimic a p-value by dividing the posterior mean log odds ratio by the posterior standard deviation of this $\beta$
* Also get Bayesian posterior probability of an effect, which is more actionable than a p-value
```{r}
f <- blrm(y ~ drug + cluster(id), data=d)
f
draws <- f$draws[, 'drug=B']
beta <- mean(draws)
se <- sd(draws)
z <- beta / se
p <- 2 * (1 - pnorm(abs(z)))
P <- mean(draws > 0)
round(c(beta=beta, se=se, z=z, p=p, 'Pr(beta > 0)'=P), 3)
```
* Compare the p=0.007 with the rank difference tests's p=0.009
* Note that $\beta$ is on the log-odds scale and cannot be compared to a difference in means
* Semiparametric models can be used to estimate means, quantiles, etc. (@sec-nonpar-2way)
* Try an ordinary PO model with a cluster sandwich covariance estimator
```{r}
f <- orm(y ~ drug, x=TRUE, y=TRUE)
robcov(f, id)
```
* The result is reasonable
* [Simulations show](https://fharrell.com/post/pair) that the cluster sandwich estimator of the standard error of the estimated effect has excellent operating characteristics
## Power and Sample Size
### Normal Approximation
* Common to get power/sample size estimates for the Wilcoxon two-sample comparison using the unpaired $t$-test power formula
* Are assuming normality and (usually) equal variances
* To reflect the slight inefficiency of the Wilcoxon two-sample test if normality were to magically hold, multiply the $t$-test sample size by $\frac{3}{\pi} = 1.047$
* When the response within-group distribution is far from normal this approach is suspect
+ e.g., $Y$ has many ties at one value, has a floor or ceiling effect, is asymmetric, or has heavy tails
* Need a general approach
### More on Relative Efficiency
* Relative efficiency of $\frac{3}{\pi}$ for the Wilcoxon 2-sample test can be derived as a correlation coefficient
* As $n \rightarrow \infty$ it is the squared correlation between the weights Wilcoxon gives to order statistics (sorted data values) and the optimal weights
* Wilcoxon is a _linear rank statistic_ with weights equal to ordinary ranks
* Optimal linear rank test (normal scores test) for a normal distribution uses the probit link (normal inverse weights), i.e., $\Phi^{-1}(\frac{\mathrm{ranks}}{n+1})$
* Compute correlation of ordinary ranks with normal scores
```{r rankeff}
for(n in c(10, 100, 1000, 10000, 100000, 1000000)) {
ranks <- 1 : n
zranks <- qnorm(ranks / (n + 1))
cat('n:', n, ' r2:', cor(ranks, zranks)^2, '\n')
}
cat('3/pi: ', 3 / pi, '\n')
```
### Tailoring Power Calculations to the Wilcoxon Test {#sec-nonpar-popower}
* Whitehead @whi93sam derived simple formulas related to the proportional odds model score test
* Formulas assume that a frequency-tabulated distribution estimate is available for the combined groups
* Power is computed as a function of the group 2 : group 1 odds ratio for exceedance probabilities
* See example below for conversion of ORs to differences in means or medians
+ OR=1 $\rightarrow$ distributions are the same, so differences in means/medians are zero
* See `R` `Hmisc` package `popower` and `posamsize` functions
* See [this](https://fharrell.com/post/pop) for more detailed examples of power and sample size calculation sfor the PO model
### Discrete $Y$
* Example: response variable has clumping at zero (with prob. 0.3) and is otherwise uniformly distributed over the values 1, 2, 4, 8, 16, 32, 64
+ note: actual data values do not affect power Calculations
+ don't come into play until translate to means/medians
```{r popower}
p <- c(.3, rep(.1, 7))
popower(p, 1.25, 1000) # compute power to detect OR=1.25, combined N=1000
posamsize(p, 1.25, power=0.9) # N for power=0.9
```
* Show how cell probabilities are translated by OR=1.25, and compute the mean and median of Y for a series of ORs for simpler interpretation
```{r popower2}
pomodm(p=p, odds.ratio=1.25)
x <- c(0, 2 ^ (0:6))
sum(p * x) # check mean with OR=1
ors <- c(1, 1.05, 1.1, 1.2, 1.25, 1.5, 2)
w <- matrix(NA, nrow=length(ors), ncol=2,
dimnames=list(OR=ors, c('mean', 'median')))
i <- 0
for(or in ors) {
i <- i + 1
w[i, ] <- pomodm(x, p, odds.ratio=or)
}
w
```
### Gaussian $Y$
* Suppose response variable for control group has a normal distribution with mean 100 and SD 10
* Start by assuming the experimental arm has the same distribution as control except with the mean shifted upwards 3 units
* This will result in non-proportional odds so the Wilcoxon test is not optimal but will still be 0.95 efficient
* When the sample size per group is 150, the power of the $t$-test to detect a 3-unit difference in means is:
```{r powert}
require(pwr)
pwr.t.test(d=3 / 10, n=150, sig.level=0.05, type='two.sample')
```
* To get the power of the Wilcoxon test when both populations have a normal distribution, we can easily use simulation
```{r powerwsim}
getRs('hashCheck.r') # defines runifChanged
s <- 1000 # number of simulated trials
pval <- numeric(s)
set.seed(1) # so can reproduce results
for(i in 1 : s) {
y1 <- rnorm(150, 100, 10)
y2 <- rnorm(150, 103, 10)
w <- wilcox.test(y1, y2)
pval[i] <- w$p.value
}
mean(pval < 0.05) # proportion of simulations with p < 0.05
# Simulate the power by actually running the prop. odds model 300 times
g <- function() simRegOrd(300, nsim=400, delta=3, sigma=10)$power # slower
as.vector(runifChanged(g))
```
* For the Wilcoxon test to be optimal (PO holds) shifting the control distribution by an odds ratio will result in a non-Gaussian distribution for the experimental arm
* Solve for the odds ratio that shifts the mean from 100 to 103, assume PO and compute the power
```{r powerwmean}
#| label: fig-nonpar-powerwmean
#| fig-cap: "Relationship between odds ratio and assumed mean in the experimental arm"
#| fig-height: 3.5
#| fig-width: 4.25
# Use an arbitrary large sample to mimic population computations
m <- 200000
y1 <- sort(rnorm(m, 100, 10))
ors <- means <- seq(1, 4, by=.025)
i <- 0
for(or in ors) {
i <- i + 1
means[i] <- pomodm(y1, rep(1/m, m), odds.ratio=or)['mean']
}
needed.or <- approx(means, ors, xout=103)$y
needed.or
ggplot(mapping=aes(ors, means)) + geom_line() +
geom_hline(yintercept=103, alpha=I(0.25)) +
geom_vline(xintercept=needed.or, alpha=I(0.25)) +
xlab('Group B:A Odds Ratio') +
ylab('Mean in Population B')
# Compute power at that odds ratio assuming no ties in data
popower(rep(1/300, 300), odds.ratio=needed.or, n=300)
```
* Check how non-normal the experimental arm responses would be if PO holds and OR=10
```{r hownn}
#| label: fig-nonpar-nownn
#| fig-cap: "Assessing departure from normality in the experimental arm that is induced by assuming proportional odds instead of a shift in means. The nearly equivalent normal distribution was determined by matching quartiles of the distribution to the logistic distribution."
#| fig-scap: "Departure from normality induced by assuming proportional odds"
#| fig-height: 3.5
#| fig-width: 4.25
# First do this theoretically
# Control arm has Gaussian Y with mean 100, SD 10
# Create experimental arm distribution using OR=10
y <- seq(60, 145, length=150)
Fy <- 1 - pnorm(y, mean=100, sd=10) # P(Y >= y | group A)
Gy <- 1 - plogis(qlogis(Fy) + log(10)) # P(Y >= y | group B)
qu <- approx(Gy, y, xout=c(0.25, 0.5, 0.75))$y
qu # Q1, median, Q2
s <- (qu[3] - qu[1]) / (qnorm(0.75) - qnorm(0.25))
mu <- qu[1] - s * qnorm(0.25)
ncdf <- pnorm(y, mean=mu, sd=s)
d <- rbind(data.frame(Distribution='logistic', x=y, y=Gy),
data.frame(Distribution='normal', x=y, y=ncdf))
ggplot(d, aes(x, y, col=Distribution)) + geom_line() +
xlab(expression(y)) + ylab(expression(P(Y <= y)))
```
```{r hownn2}
#| label: fig-nonpar-hownn2
#| fig-cap: "Theoretical $q-q$ plot assessing normality of experimental arm distribution induced by proportional odds"
#| fig-height: 3.5
#| fig-width: 4.25
#| fig-scap: "Assessing normality of experimental arm"
ggplot(mapping=aes(x=y, y=qnorm(Gy))) + geom_line() +
geom_smooth(method=lm, se=FALSE, col=I('blue')) +
xlab(expression(y))
```
```{r hownn3}
#| label: fig-nonpar-hownn3
#| fig-cap: "Creation of 200,000 point discrete distribution for the experimental arm, obtained by converting the control distribution under proportional odds. Blue curve is the normal cumulative distribution function; black curve is for the experimental arm assuming a proportional odds shift from the control arm."
#| fig-scap: "Discrete distribution for the experimental arm"
#| fig-height: 3.5
#| fig-width: 4.25
p <- pomodm(p=rep(1/m, m), odds.ratio=10)
range(p) # control arm: all 1/200000
wtd.mean(y1, p) # mean shifted by about 12 units
# Form new distribution by repeating each observation a number
# of times equal to the ratio of the new probability to the
# minimum of all new probabilities
y2 <- rep(y1, round(p / min(p))) # 2M obs instead of 200K
mean(y2)
quantile(y2, c(.25, .5, .75))
# The following plot is similar to the previous one
ncdf <- pnorm(y, mean=mean(y2), sd=sd(y2))
ggplot(mapping=aes(x=y2)) + stat_ecdf(geom='step') +
geom_line(mapping=aes(x=y, y=ncdf, col=I('blue'))) +
xlab(expression(y)) + ylab(expression(Proportion <= x))
```
* Little non-normality of the 2nd group if the treatment effect operates by multiplying the odds that $Y \geq y$ instead of incrementing the mean
+ relates to similarity of normal and logistic distributions
### Heavy-tailed $Y$
* Get power to detect a shift in mean of 0.3 units for a heavy-tailed control distribution (t with 4 d.f.) with 150 subjects per group
* Loss of efficiency of $t$-test
+ mean and SD are no longer optimal data summaries
* Can use above method to compute Wilcoxon power quickly if willing to assume PO
* Let's not assume PO, and instead use simulation
* Compare with power of $t$-test
* Do for both null and non-null cases to verify type I error prob.
```{r simtw}
s <- 1000 # number of simulated trials
pvalt <- pvalw <- numeric(s)
set.seed(1) # so can reproduce results
for(delta in c(0, 0.3)) {
for(i in 1 : s) {
y1 <- rt(150, 4)
y2 <- rt(150, 4) + delta
pvalt[i] <- t.test(y1, y2)$p.value
pvalw[i] <- wilcox.test(y1, y2)$p.value
}
cat('Delta:', delta, '\n')
P <- function(x) round(mean(x), 2)
cat('Proportion of simulations with W p-value < t p-value:',
P(pvalw < pvalt), '\n')
cat('Mean p-value for t:', P(pvalt), '\n')
cat('Mean p-value for W:', P(pvalw), '\n')
cat('Power for t:', P(pvalt < 0.05), '\n')
cat('Power for W:', P(pvalw < 0.05), '\n\n')
}
```
* `Hmisc` `simRegOrd` function can also simulate power for an adjusted two-sample comparison if there is one adjustment covariate
## Bayesian Proportional Odds Model
* PO model and other cumulative probability semiparametric ordinal regression models are readily extended to a Bayesian framework
* Need special care in selecting priors for the intercepts for the continuous $Y$ case
* `blrm` function in the [R `rmsb` package](https://hbiostat.org/r/rmsb) is devoted to the PO and partial PO model
* Nathan James has an implementation using Stan available at<br> [github.com/ntjames/bayes_cpm](https://github.com/ntjames/bayes_cpm)
* See also the `R` `brms` package: [bit.ly/brms-ordinal](http://bit.ly/brms-ordinal) and this discussion:<br> [github.com/paul-buerkner/brms/issues/762](http://github.com/paul-buerkner/brms/issues/762)
* Bayesian version of the Wilcoxon test is the posterior probability that $\beta_1 > 0$ in the PO model
* Advantages of Bayes for PO models:
+ does not need approximations such as large sample normality of $\hat{\beta}$ or $\chi^{2}$ distribution approximation to likelihood ratio test statistic
+ inference is more interpretable and direct
+ can bring outside information to the analysis
+ can incorporate shrinkage/penalization/skepticism and still have exact inference
+ automatically obtain exact distributions and credible intervals for derived quantities^[One merely takes each posterior sample for the $\alpha$s and $\beta$s and computes the quantity of interest, thereby automatically generating posterior samples for the derived quantity for which quantiles can compute credible intervals, etc.], e.g. mean, quantiles, differences in means and quantiles, differences in exceedance probs, $P(Y=y | X)$
+ can relax PO assumption without huge instabilities that result from using polytomous logistic models; prior distributions can favor PO while allowing non-PO
* See [this](https://hbiostat.org/bayes/bet/design#sec-design-popower) for simulating Bayesian power of a PO model comparison
## Sample Size Requirement for Characterizing Entire Distributions {#sec-nonpar-ecdf}
The empirical cumulative distribution function (ECDF) was introduced in @sec-desc-dist. It is a nonparametric estimator of the unknown CDF for a (primarily) continuous variable. Inverting the ECDF gives traditional sample quantile estimates, so if one wants to estimate all possible quantiles accurately one needs to estimate the ECDF accurately over its entire range.
[Kolmogorov and Smirnov](https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test) developed a nonparametric test for whether a sample comes from a specific parametric CDF, by computing the maximum absolute difference between the ECDF and the postulated CDF. This test can be inverted to obtain simultaneous confidence bands for the unknown CDF. The global margin of error for an ECDF is the Kolmogorov-Smirnov critical value, for a certain $\alpha$.
Kjetil Halvorsen and Martin Maechler have an R function in their [`sfsmisc`](https://cran.r-project.org/web/packages/sfsmisc) package that provides a fast approximation to the K-S critical values when $\alpha=0.05$ (for 0.95 confidence bands). This function is reproduced below, and we use it to compute the 0.95-level simultaneous margins of error for the ECDF as a function of sample size.
This is a good opportunity to check the universal rule that the precision of an estimate is proportional to the square root of the sample size. The `approxmoe` function below multiplies the accurate margin of error at $n=20$ by the square root of the ratio of 20 to the sample size of interest.
```{r}
#| label: fig-nonpar-kscrit
#| fig.cap: "Margin of error for an ECDF based on Kolmogorov-Smirnov critical values"
KSd <- function(n)
{
## `approx.ksD()'
## approximations for the critical level for Kolmogorov-Smirnov statistic D,
## for confidence level 0.95. Taken from Bickel & Doksum, table IX, p.483
## and Lienert G.A.(1975) who attributes to Miller,L.H.(1956), JASA
ifelse(n > 80,
1.358/( sqrt(n) + .12 + .11/sqrt(n)),## Bickel&Doksum, table IX,p.483
splinefun(c(1:9, 10, 15, 10 * 2:8),# from Lienert
c(.975, .84189, .70760, .62394, .56328,# 1:5
.51926, .48342, .45427, .43001, .40925,# 6:10
.33760, .29408, .24170, .21012,# 15,20,30,40
.18841, .17231, .15975, .14960)) (n))
}
plot(10 : 10000, KSd(10 : 10000), type='l', xlab='n',
ylab='ECDF Margin of Error')
abline(h=c(0.025, 0.05, 0.1), col=gray(0.6))
ns <- c(20, 50, 100, 180, 250, 500, 730, 750, 1000, 2935, 5000, 10000, 18400)
approxmoe <- function(n) 0.29408 * sqrt(20 / n)
data.frame(n=ns, MOE=round(KSd(ns), 3), MOEsqrt=round(approxmoe(ns), 3))
```
The sample size required to have a margin of error of $\pm 0.01$ for the entire ECDF is 18,400. In other words if one desired to have a high degree of confidence that no estimated quantile will be off by more than a probability of 0.01, $n=18,400$ will achieve this. For example, the sample 0.25 quantile (first quartile) may correspond to population quantiles 0.24-0.26. To achieve a $\pm 0.1$ MOE requires $n=180$, and to have $\pm 0.05$ requires $n=730$.
The "universal $\sqrt{}$ rule" worked quite well. This will allow us to extend the calculations to any confidence level. The built-in R function `qsmirnov` allows us to compute exact critical values of the K-S test by computing the critical value of the Smirnov test when one of the two distributions it compares has an infinite sample size. Here $n=10000$ is close enough to $\infty$.
```{r}
qsmirnov(0.95, c(20, 10000)) # took 11s
KSd(20)
# Now use alpha=0.1 instead of 0.05
qsmirnov(0.9, c(20, 10000))
approxmoe90 <- function(n) 0.2652735 * sqrt(20 / n)
round(approxmoe90(c(20, 100, 1000)), 3)
```
```{r echo=FALSE}
saveCap('07')
```