```{r include=FALSE}
require(rms)
require(ggplot2)
options(qproject='rms', prType='html')
require(qreport)
getRs('qbookfun.r')
hookaddcap()
knitr::set_alias(w = 'fig.width', h = 'fig.height', cap = 'fig.cap', scap ='fig.scap')
```
# Body Fat: Case Study in Linear Modeling {#sec-bodyfat}
* Goal: accurately estimate proportion of male adult body mass that is fat using readily available body dimensions and age
* Gold standard body fat was determined by underwater weighing
* Source: [`kaggle` competition](https://www.kaggle.com/datasets/fedesoriano/body-fat-prediction-dataset)
* Original source: Generalized body composition prediction equation for men using simple measurement techniques, K.W. Penrose, A.G. Nelson, A.G. Fisher, FACSM, Human Performance Research Center, Brigham Young University, Provo, Utah 84602 as listed in Medicine and Science in Sports and Exercise, vol. 17, no. 2, April 1985, p. 189
* 252 men; 3 excluded due to erroneous data
* Available at [hbiostat.org/data](https://hbiostat.org/data) or using `getHdata`
**Statistical Analysis Attack**
* Response variable is proportion of body mass that is fat
* Display descriptive statistics and variable clustering pattern
* Run a redundancy analysis
* Knowing that abdomen circumference is a dominating predictor and that height must be taken into account when interpreting it, learn about the transformations of the variables from a linear model with predictors abdomen, height, and age
* Compare 4 competing models with AIC
* Assess the contribution of all other size measurements in predicting fat
## Descriptive Statistics
```{r}
getHdata(bodyfat)
d <- bodyfat
dd <- datadist(d); options(datadist='dd')
des <- describe(d)
sparkline::sparkline(0) # load jQuery javascript for sparklines
print(des, which='continuous')
plot(varclus(~ . - fat, data=d)) # remove Y from clustering
```
Do a redundancy analysis
```{r}
# Don't allow response variable to be used
r <- redun(~ . -fat, data=d)
r
# Show strongest relationships among transformed predictors
r2describe(r$scores, nvmax=4)
```
`weight` could be dispensed with but we will keep it for historical reasons.
## Learn Predictor Transformations and Interactions From Simple Model
* Compare AICs of 5 competing models
* It is safe to use AIC to select from among perhaps 3 models so we are pushing the envelope here
```{r}
AIC(ols(fat ~ rcs(age, 4) + rcs(height, 4) * rcs(abdomen, 4), data=d))
AIC(ols(fat ~ rcs(age, 4) + rcs(log(height), 4) + rcs(log(abdomen), 4), data=d))
AIC(ols(fat ~ rcs(age, 4) + log(height) + log(abdomen), data=d))
AIC(ols(fat ~ age * (log(height) + log(abdomen)), data=d))
AIC(ols(fat ~ age + height + abdomen, data=d))
```
* Third model has lowest AIC
* Will use its structure when adding other predictors
* Check contant variance and normality assumptions on the winning small model
```{r}
f <- ols(fat ~ rcs(age, 4) + log(height) + log(abdomen), data=d)
f
pdx <- function() {
r <- resid(f)
w <- data.frame(r=r, fitted=fitted(f))
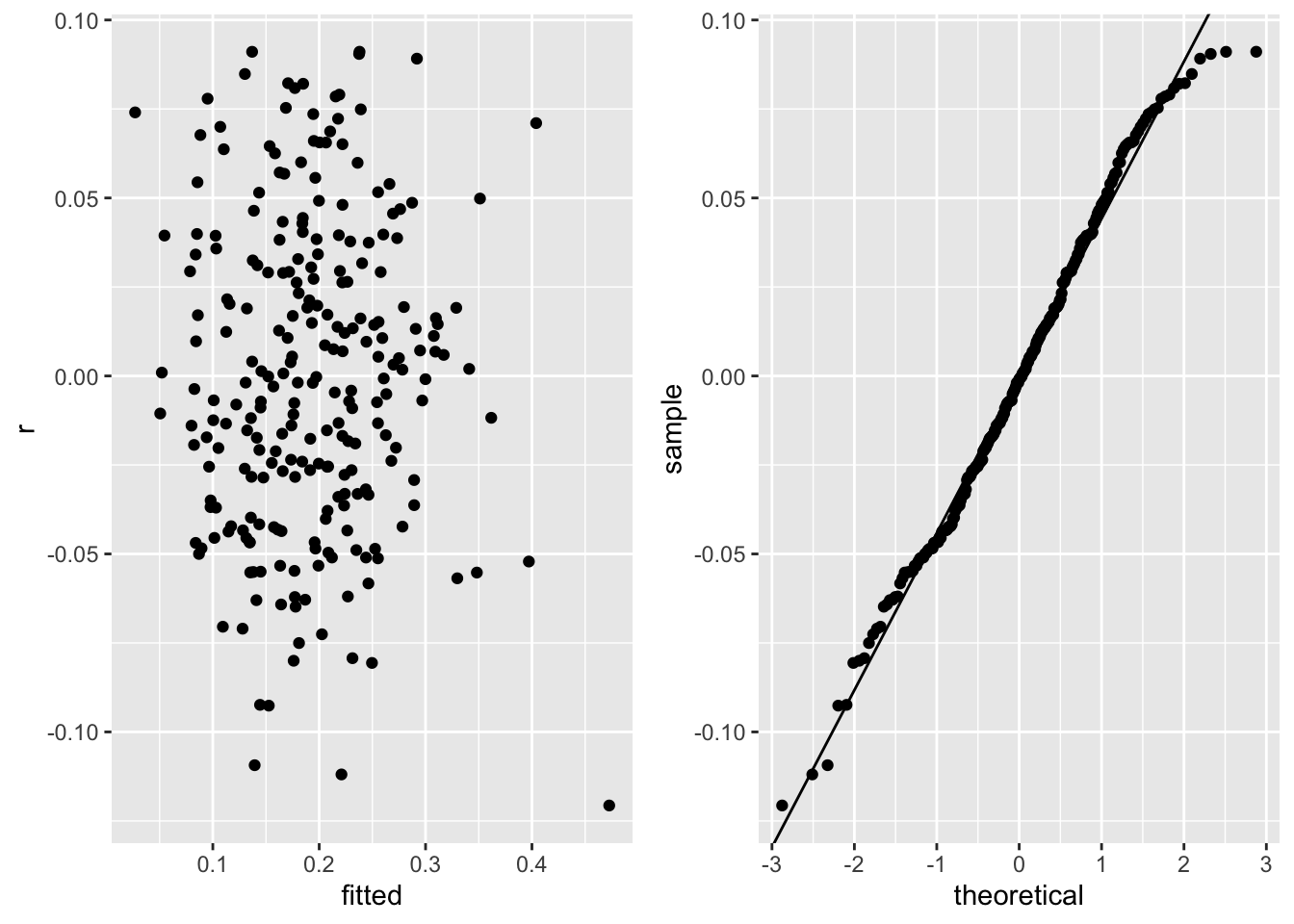
p1 <- ggplot(w, aes(x=fitted, y=r)) + geom_point()
p2 <- ggplot(w, aes(sample=r)) + stat_qq() +
geom_abline(intercept=mean(r), slope=sd(r))
gridExtra::grid.arrange(p1, p2, ncol=2)
}
pdx()
```
* Normal and constant variance (across predicted values) on the original fat scale
* Usually would need to transform a [0,1]-restricted variable
* Luckily no predicted values outside [0,1] in the dataset
* Will keep a linear model on untransformed fat
## Assess Predictive Discrimination Added by Other Size Variables
```{r}
g <- ols(fat ~ rcs(age, 4) + log(height) + log(abdomen) + log(weight) + log(neck) +
log(chest) + log(hip) + log(thigh) + log(knee) + log(ankle) + log(biceps) +
log(forearm) + log(wrist), data=d, x=TRUE, y=TRUE)
AIC(g)
```
* By AIC the large model is better
* $R^{2}_\text{adj}$ went from 0.704 to 0.733
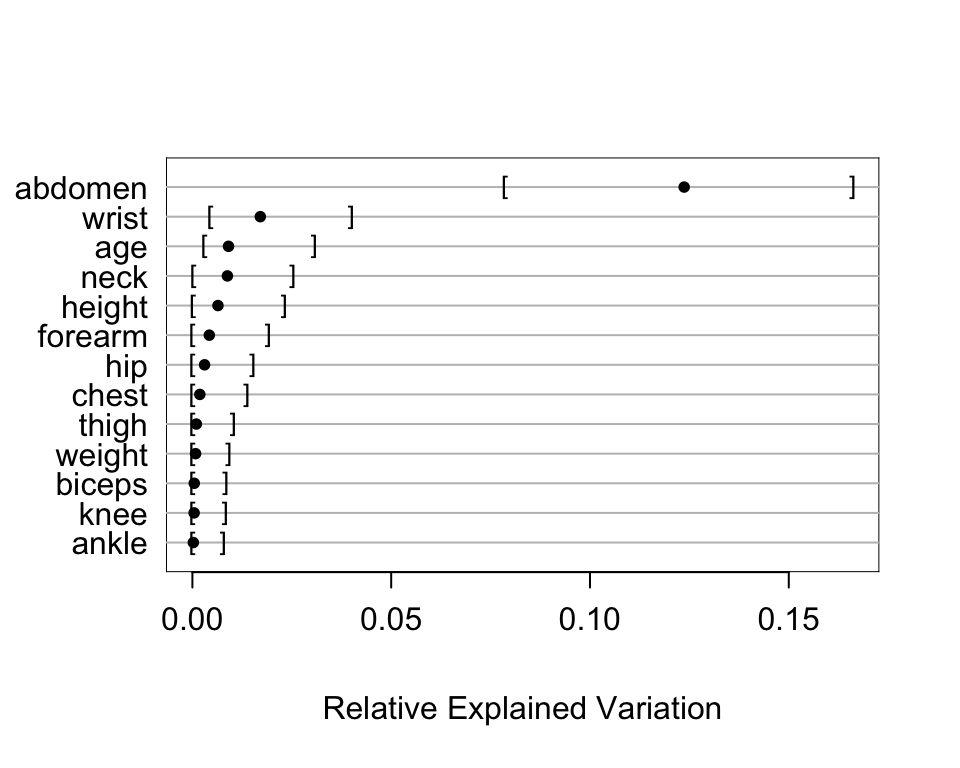
* Estimate relative explained variation of each variable in this larger model, with bootstrap confidence intervals
```{r}
#| fig-height: 4
#| fig-width: 5
b <- bootcov(g, B=500, coef.reps=TRUE)
r <- rexVar(b, d)
plot(r)
```
* Because of collinearities, the competition between predictors makes interpretation more difficult
* How does the larger model's increased $R^2$ translate to improvement in median prediction error?
```{r}
median(abs(resid(f)))
median(abs(resid(g)))
```
* There is a reduction of 0.003 in the typical prediction error
* Proportion of fat varies from 0.06 - 0.32 (0.05 quantile to 0.95 quantile)
* Additional variables are not worth it
* A typical prediction error of 0.03 makes the model fit for purpose
## Model Interpretation
* Image plot
* Nomogram
```{r}
#| label: fig-bodyfat-bplot
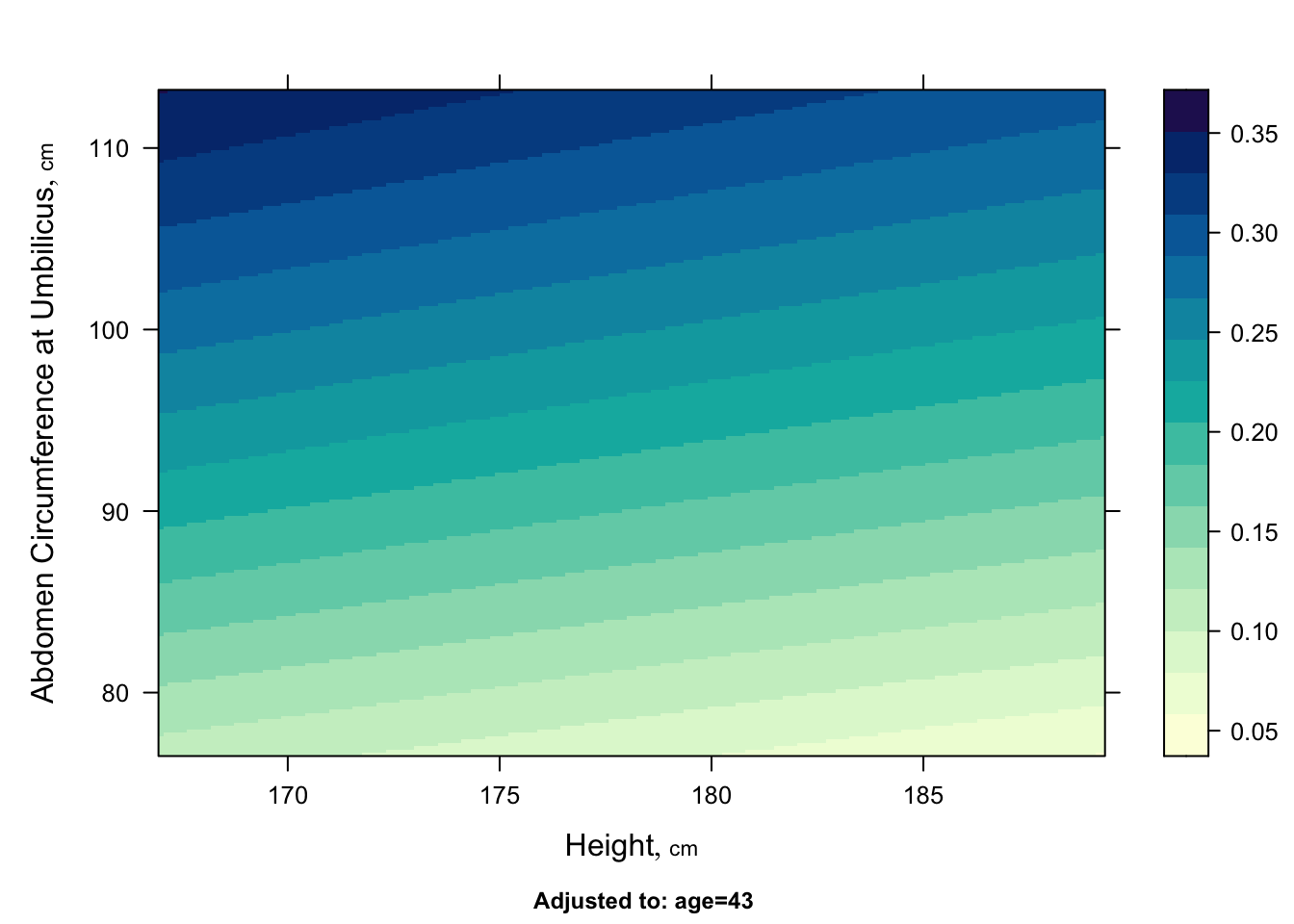
#| fig-cap: "Predicted body fat fraction for varying height and weight given age of 43 and other predictors set to their medians/modes"
p <- Predict(f, height, abdomen)
bplot(p, ylabrot=90)
```
```{r}
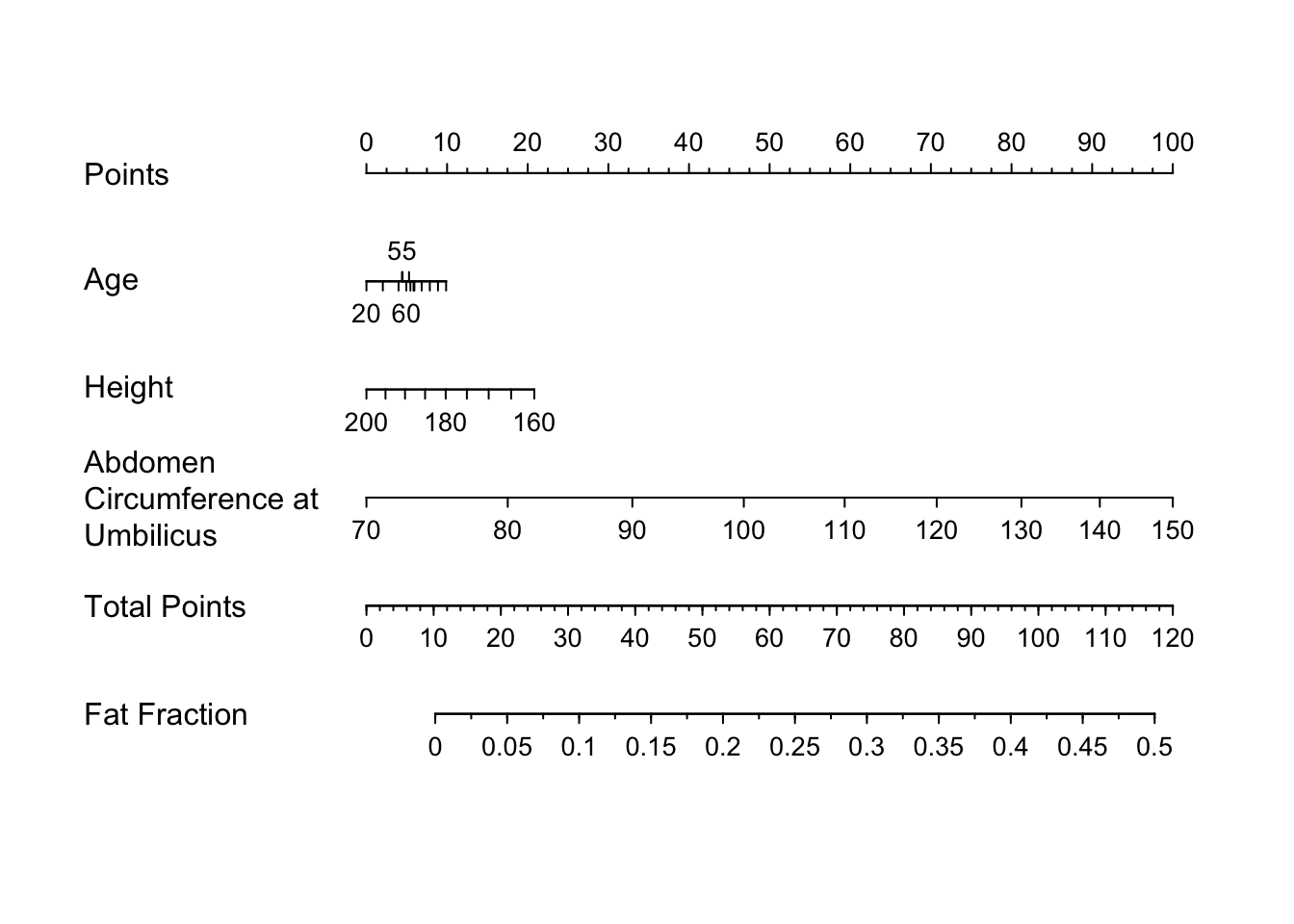
#| label: fig-bodyfat-nomo
#| fig-cap: "Nomogram for estimating body fat fraction from all predictors"
plot(nomogram(f), lplab='Fat Fraction')
```
```{r echo=FALSE}
saveCap('23')
```