Code
f <- lrm(y ~ sex + race + rcs(age,5) + rcs(weight,5) +
rcs(height,5) + rcs(blood.pressure,5))
plot(anova(f))Scientific Big Picture
Modeling Strategy in a Nutshell
There are many choices to be made when deciding upon a global modeling strategy, including choice between
Motivating examples:
# Overfitting a flat relationship
require(rms)
set.seed(1)
x <- runif(1000)
y <- runif(1000, -0.5, 0.5)
dd <- datadist(x, y); options(datadist='dd')
par(mfrow=c(2,2), mar=c(2, 2, 3, 0.5))
pp <- function(actual) {
yhat <- predict(f, data.frame(x=xs))
yreal <- actual(xs)
plot(0, 0, xlim=c(0,1),
ylim=range(c(quantile(y, c(0.1, 0.9)), yhat,
yreal)),
type='n', axes=FALSE)
axis(1, labels=FALSE); axis(2, labels=FALSE)
lines(xs, yreal)
lines(xs, yhat, col='blue')
}
f <- ols(y ~ rcs(x, 5))
xs <- seq(0, 1, length=150)
pp(function(x) 0*x)
title('Mild Error:\nOverfitting a Flat Relationship',
cex=0.5)
y <- x + runif(1000, -0.5, 0.5)
f <- ols(y ~ rcs(x, 5))
pp(function(x) x)
title('Mild Error:\nOverfitting a Linear Relationship',
cex=0.5)
y <- x^4 + runif(1000, -1, 1)
f <- ols(y ~ x)
pp(function(x) x^4)
title('Serious Error:\nUnderfitting a Steep Relationship',
cex=0.5)
y <- - (x - 0.5) ^ 2 + runif(1000, -0.2, 0.2)
f <- ols(y ~ x)
pp(function(x) - (x - 0.5) ^ 2)
title('Tragic Error:\nMonotonic Fit to\nNon-Monotonic Relationship',
cex=0.5)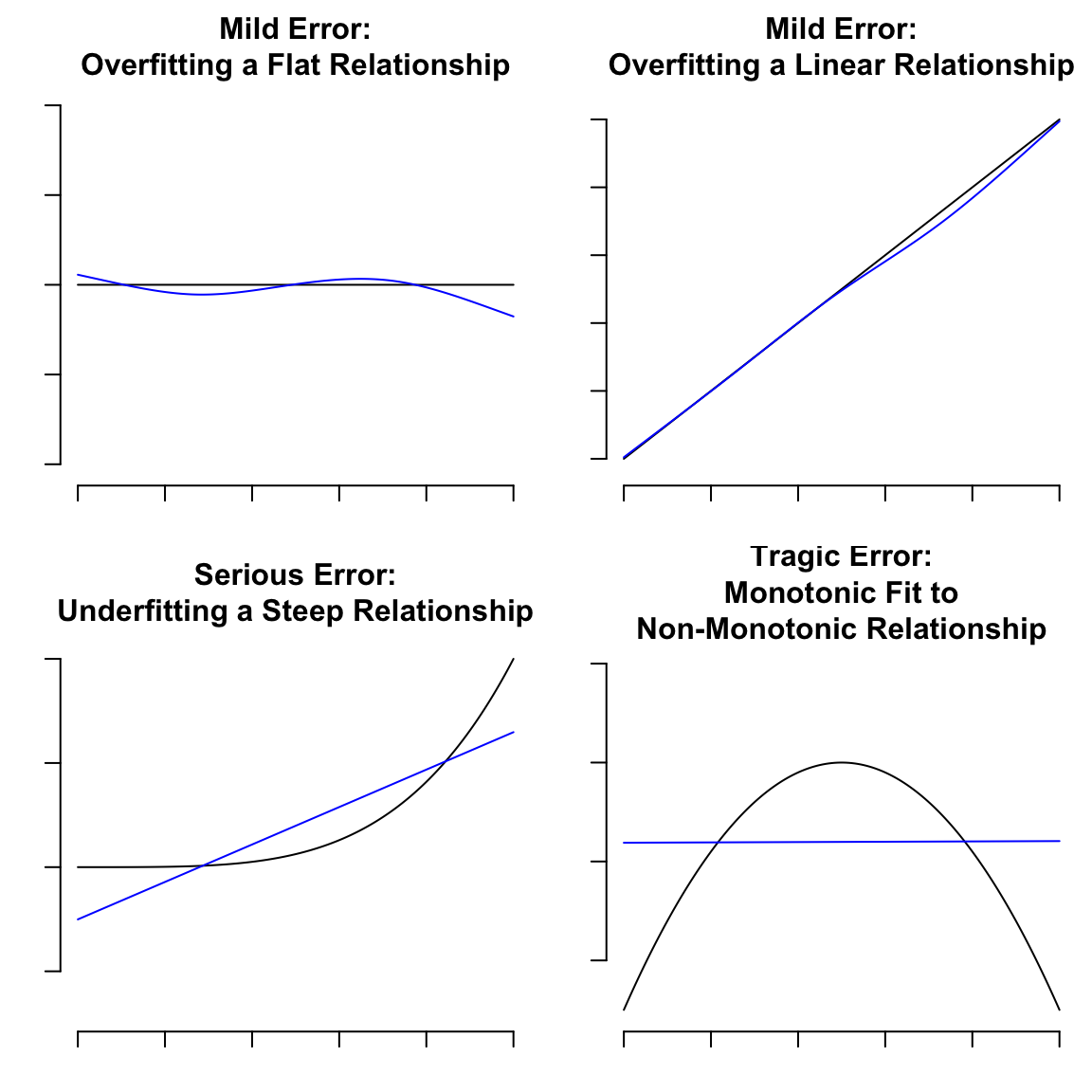
| Categorical predictor with \(k\) levels | Collapse less frequent categories into “other” |
| Continuous predictor represented as \(k\)-knot restricted cubic spline | Reduce \(k\) to a number as low as 3, or 0 (linear) |
When the effective sample size available is sufficiently large so that a saturated main effects model may be fitted, a good approach to gauging predictive potential is the following.
Commands in the rms package can be used to plot only what is needed. Here is an example for a logistic model.
When collinearities or confounding are not problematic, a quicker approach based on pairwise measures of association can be useful. This approach will not have numerical problems (e.g., singular covariance matrix) and is based on:
1 This test statistic does not inform the analyst of which groups are different from one another.
Allocating d.f. based on partial tests of association or sorting \(\rho^2\) is a fair procedure because
Initial simulations show the procedure to be conservative. Note that one can move from simpler to more complex models but not the other way round
2 Lockhart et al. (2013) provide an example with \(n=100\) and 10 orthogonal predictors where all true \(\beta\)s are zero. The test statistic for the first variable to enter has type I assertion probability of 0.39 when the nominal \(\alpha\) is set to 0.05.
- The degree of correlation between the predictor variables affected the frequency with which authentic predictor variables found their way into the final model.
- The number of candidate predictor variables affected the number of noise variables that gained entry to the model.
- The size of the sample was of little practical importance in determining the number of authentic variables contained in the final model.
- The population multiple coefficient of determination could be faithfully estimated by adopting a statistic that is adjusted by the total number of candidate predictor variables rather than the number of variables in the final model.
Simulation experiment, true \(\sigma^{2} = 6.25\), 8 candidate variables, 4 of them related to \(Y\) in the population. Select best model using all possible subsets regression to maximize \(R^{2}_{adj}\) (all possible subsets is not usually recommended but gives variable selection more of a chance to work in this context).
Note: The audio was made using stepAIC with collinearities in predictors. The code below allows for several options. Here we use all possible subsets of predictors and force predictors to be uncorrelated, which is the easiest case for variable selection.
require(MASS) # provides stepAIC function
require(leaps) # provides regsubsets function
sim <- function(n, sigma=2.5, method=c('stepaic', 'leaps'),
pr=FALSE, prcor=FALSE, dataonly=FALSE) {
method <- match.arg(method)
if(uncorrelated) {
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- rnorm(n)
x5 <- rnorm(n)
x6 <- rnorm(n)
x7 <- rnorm(n)
x8 <- rnorm(n)
}
else {
x1 <- rnorm(n)
x2 <- x1 + 2.0 * rnorm(n) # was + 0.5 * rnorm(n)
x3 <- rnorm(n)
x4 <- x3 + 1.5 * rnorm(n)
x5 <- x1 + rnorm(n)/1.3
x6 <- x2 + 2.25 * rnorm(n) # was rnorm(n)/1.3
x7 <- x3 + x4 + 2.5 * rnorm(n) # was + rnorm(n)
x8 <- x7 + 4.0 * rnorm(n) # was + 0.5 * rnorm(n)
}
z <- cbind(x1,x2,x3,x4,x5,x6,x7,x8)
if(prcor) return(round(cor(z), 2))
lp <- x1 + x2 + .5*x3 + .4*x7
y <- lp + sigma*rnorm(n)
if(dataonly) return(list(x=z, y=y))
if(method == 'leaps') {
s <- summary(regsubsets(z, y))
best <- which.max(s$adjr2)
xvars <- s$which[best, -1] # remove intercept
ssr <- s$rss[best]
p <- sum(xvars)
xs <- if(p == 0) 'none' else paste((1 : 8)[xvars], collapse='')
if(pr) print(xs)
ssesw <- (n - 1) * var(y) - ssr
s2s <- ssesw / (n - p - 1)
yhat <- if(p == 0) mean(y) else fitted(lm(y ~ z[, xvars]))
}
f <- lm(y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8)
if(method == 'stepaic') {
g <- stepAIC(f, trace=0)
p <- g$rank - 1
xs <- if(p == 0) 'none' else
gsub('[ <br>+x]','', as.character(formula(g))[3])
if(pr) print(formula(g), showEnv=FALSE)
ssesw <- sum(resid(g)^2)
s2s <- ssesw/g$df.residual
yhat <- fitted(g)
}
# Set SSEsw / (n - gdf - 1) = true sigma^2
gdf <- n - 1 - ssesw / (sigma^2)
# Compute root mean squared error against true linear predictor
rmse.full <- sqrt(mean((fitted(f) - lp) ^ 2))
rmse.step <- sqrt(mean((yhat - lp) ^ 2))
list(stats=c(n=n, vratio=s2s/(sigma^2),
gdf=gdf, apparentdf=p, rmse.full=rmse.full, rmse.step=rmse.step),
xselected=xs)
}
rsim <- function(B, n, method=c('stepaic', 'leaps')) {
method <- match.arg(method)
xs <- character(B)
r <- matrix(NA, nrow=B, ncol=6)
for(i in 1:B) {
w <- sim(n, method=method)
r[i,] <- w$stats
xs[i] <- w$xselected
}
colnames(r) <- names(w$stats)
s <- apply(r, 2, median)
p <- r[, 'apparentdf']
s['apparentdf'] <- mean(p)
print(round(s, 2))
print(table(p))
cat('Prob[correct model]=', round(sum(xs == '1237')/B, 2), '\n')
}Show the correlation matrix being assumed for the \(X\)s:
x1 x2 x3 x4 x5 x6 x7 x8
x1 1.00 0.00 -0.01 0.00 0.01 0.01 0.00 0.01
x2 0.00 1.00 0.00 0.00 0.01 0.00 0.00 0.00
x3 -0.01 0.00 1.00 0.00 0.00 0.00 0.00 -0.01
x4 0.00 0.00 0.00 1.00 0.01 0.00 0.00 0.01
x5 0.01 0.01 0.00 0.01 1.00 0.01 0.00 0.00
x6 0.01 0.00 0.00 0.00 0.01 1.00 0.00 0.00
x7 0.00 0.00 0.00 0.00 0.00 0.00 1.00 0.01
x8 0.01 0.00 -0.01 0.01 0.00 0.00 0.01 1.00Simulate to find the distribution of the number of variables selected, the proportion of simulations in which the true model (\(X_{1}, X_{2}, X_{3}, X_{7}\)) was found, the median value of \(\hat{\sigma}^{2}/\sigma^{2}\), the median effective d.f., and the mean number of apparent d.f., for varying sample sizes.
n vratio gdf apparentdf rmse.full rmse.step
20.00 0.94 5.32 4.10 1.62 1.58
p
1 2 3 4 5 6 7 8
3 14 18 22 27 11 4 1
Prob[correct model]= 0.02 n vratio gdf apparentdf rmse.full rmse.step
40.00 0.61 17.89 4.38 1.21 1.24
p
2 3 4 5 6 7
9 18 24 29 15 5
Prob[correct model]= 0.04 n vratio gdf apparentdf rmse.full rmse.step
150.00 0.44 85.99 5.01 0.59 0.57
p
2 3 4 5 6 7 8
1 5 27 35 24 7 1
Prob[correct model]= 0.2 n vratio gdf apparentdf rmse.full rmse.step
300.00 0.42 177.01 5.16 0.43 0.40
p
4 5 6 7 8
27 42 20 10 1
Prob[correct model]= 0.26 n vratio gdf apparentdf rmse.full rmse.step
2000.00 1.00 6.43 4.58 0.17 0.15
p
4 5 6 7
53 37 9 1
Prob[correct model]= 0.53 As \(n\uparrow\) the mean number of variables selected increased. The proportion of simulations in which the correct model was found increased from 0 to 0.53. \(\sigma^{2}\) is underestimated when \(n=300\) by a factor of 0.42, resulting in the d.f. needed to de-bias \(\hat{\sigma^{2}}\) being greater than \(n\) when the apparent d.f. was only 5.16 on the average. Variable selection slightly increased closeness to the true \(X\beta\).
If the simulations are re-run allowing for collinearities (uncorrelated=FALSE) one can expect variable selection to be even more problematic.
Variable selection methods (Harrell, 1986):
See also these articles:
Some of the information in the data is spent on variable selection instead of using all information for estimation.
Model specification is preferred to model selection.
Information content of the data usually insufficient for reliable variable selection.

Maxwell imagines one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. Likewise, when a slower-than-average molecule from B flies towards the trapdoor, the demon will let it pass from B to A. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics.
Szilárd pointed out that a real-life Maxwell’s demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy. Since the demon and the gas are interacting, we must consider the total entropy of the gas and the demon combined. The expenditure of energy by the demon will cause an increase in the entropy of the demon, which will be larger than the lowering of the entropy of the gas.
Source: commons.wikimedia.org/wiki/File:YoungJamesClerkMaxwell.jpg
en.wikipedia.org/wiki/Maxwell’s_demon
Peter Ellis’ blog article contains excellent examples of issues discussed here but applied to time series modeling.
3 The sample size needed for these is model-dependent
| Type of Response Variable | Limiting Sample Size \(m\) |
|---|---|
| Continuous | \(n\) (total sample size) |
| Binary | \(3nq(1-q), q=\frac{n_{2}}{n}\) 4 |
| Ordinal (\(k\) categories) | \(n - \frac{1}{n^{2}} \sum_{i=1}^{k} n_{i}^{3}\) 5 |
| Failure (survival) time | number of failures 6 |
4 If one considers the power of a two-sample binomial test compared with a Wilcoxon test if the response could be made continuous and the proportional odds assumption holds, the effective sample size for a binary response is \(3 n_{1}n_{2}/n \approx 3 \min(n_{1}, n_{2})\) if \(\frac{n_{1}}{n}\) is near 0 or 1 (Whitehead, 1993, Eq. 10, 15). Here \(n_{1}\) and \(n_{2}\) are the marginal frequencies of the two response levels (Peduzzi et al., 1996). The effective sample size is a maximum (\(0.75n\)) when \(n_{1}=n_{2}\), i.e. \(q=\frac{1}{2}\) .
5 Based on the power of a proportional odds model two-sample test when the marginal cell sizes for the response are \(n_{1}, \ldots, n_{k}\), compared with all cell sizes equal to unity (response is continuous) (Whitehead, 1993, Eq. 3). If all cell sizes are equal, the relative efficiency of having \(k\) response categories compared to a continuous response is \(1 - \frac{1}{k^{2}}\) (Whitehead, 1993, Eq. 14), e.g., a 5-level response is almost as efficient as a continuous one if proportional odds holds across category cutoffs.
6 This is approximate, as the effective sample size may sometimes be boosted somewhat by censored observations, especially for non-proportional hazards methods such as Wilcoxon-type tests (BENEDETTI et al., 1982).
To derive the effective sample size for binary \(Y\) we compare two samples of equal size \(\frac{n}{2}\) by testing whether the log odds ratio is zero. When the two samples come from populations with equal \(\Pr(Y=1) = q\), the variance of the log odds ratio is approximately \(2 \times \frac{1}{\frac{n}{2}q(1-q)} = \frac{4}{nq(1-q)}\). When \(Y\) is continuous with no ties and a Wilcoxon or proportional odds model test is used, the reciprocal of the variance of the proportional odds model’s log odds ratio is \(\frac{n^{3}}{12 (n+1)^{2}} \times (1 - \frac{1}{n^{2}}) \approx \frac{n}{12}\) so the variance is approximately \(\frac{12}{n}\). The ratio of this to the binary \(Y\) variance is \(3q(1-q)\).
set.seed(123)
n <- 50
y <- runif(20*n)
group <- rep(1:20,each=n)
ybar <- tapply(y, group, mean)
ybar <- sort(ybar)
plot(1:20, ybar, type='n', axes=FALSE, ylim=c(.3,.7),
xlab='Group', ylab='Group Mean')
lines(1:20, ybar)
points(1:20, ybar, pch=20, cex=.5)
axis(2)
axis(1, at=1:20, labels=FALSE)
for(j in 1:20) axis(1, at=j, labels=names(ybar)[j])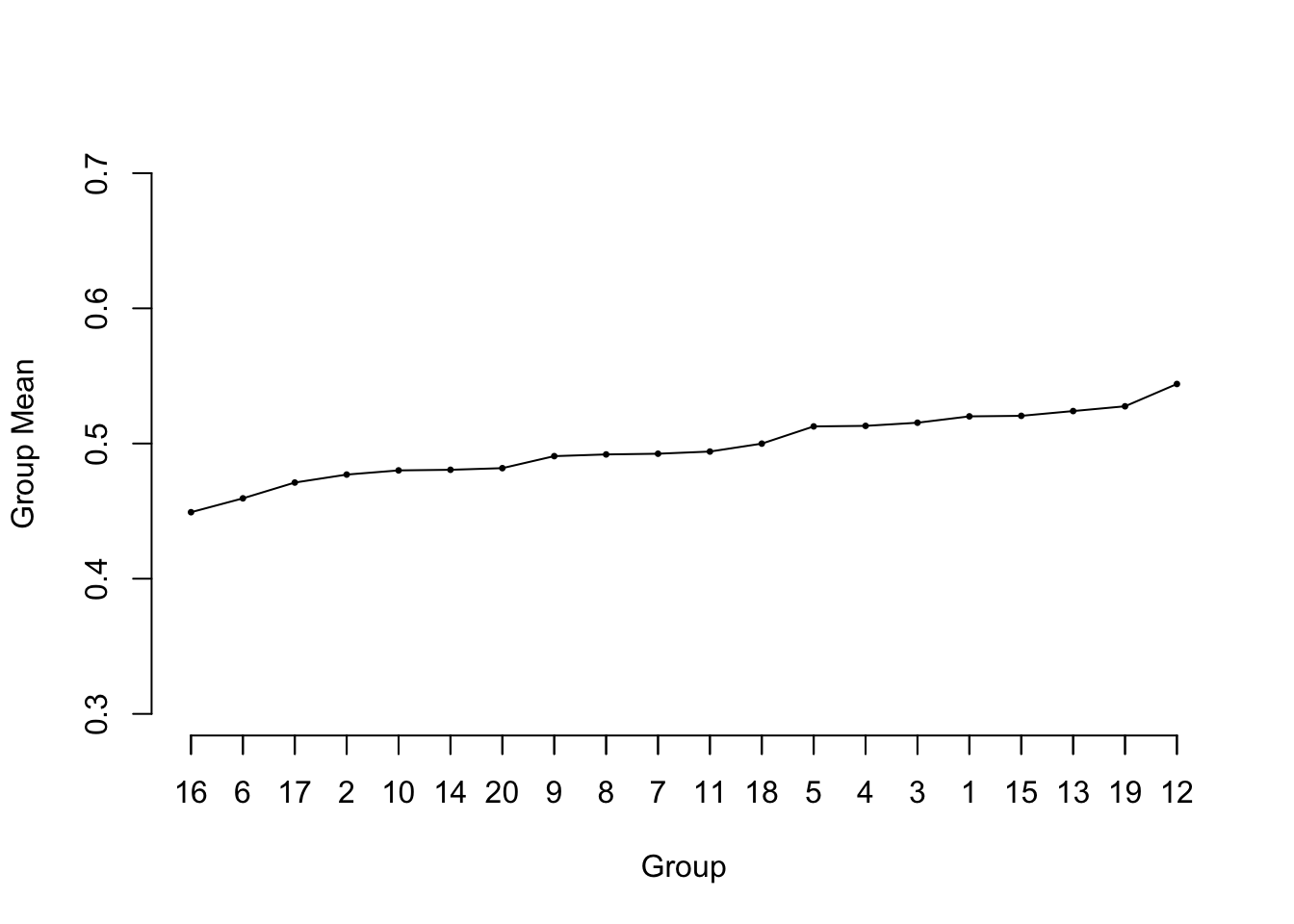
Prevent shrinkage by using pre-shrinkage
Spiegelhalter (1986): var. selection arbitrary, better prediction usually results from fitting all candidate variables and using shrinkage
Shrinkage closer to that expected from full model fit than based on number of significant variables (Copas, 1983)
Ridge regression (le Cessie & van Houwelingen, 1992; van Houwelingen & le Cessie, 1990)
Penalized MLE (Gray, 1992; Harrell et al., 1998; Verweij & van Houwelingen, 1994)
Heuristic shrinkage parameter of van Houwelingen and le Cessie (van Houwelingen & le Cessie, 1990, Eq. 77) \[\hat{\gamma} = \frac{{\rm model}\ \chi^{2} - p}{{\rm model}\ \chi^{2}}, \tag{4.1}\]
OLS7: \(\hat{\gamma} = \frac{n-p-1}{n-1} R^{2}_{\rm adj} / R^{2}\)
\(R^{2}_{\rm adj} = 1 - (1 - R^{2})\frac{n-1}{n-p-1}\)
\(p\) close to no. candidate variables
Copas (1983) (Eq. 8.5) adds 2 to numerator
VARCLUS procedure (Sarle, 1990), R varclus function, other clustering techniques: group highly correlated variablesR function redun in Hmisc packageExample: Figure 15.6
Reduce \(p\) by estimating transformations using associations with other predictors
Purely categorical predictors – correspondence analysis (Ciampi et al., 1986; Crichton & Hinde, 1989; Greenacre, 1988; Leclerc et al., 1988; Michailidis & de Leeuw, 1998)
Mixture of qualitative and continuous variables: qualitative principal components
Maximum total variance (MTV) of Young, Takane, de Leeuw (Michailidis & de Leeuw, 1998; Young et al., 1978)
Maximum generalized variance (MGV) method of Sarle (Kuhfeld, 2009, pp. 1267–1268)
MTV (PC-based instead of canonical var.) and MGV implemented in SAS PROC PRINQUAL (Kuhfeld, 2009)
R transcan Function for Data Reduction & Imputation
Initialize missings to medians (or most frequent category)
Initialize transformations to original variables
Take each variable in turn as \(Y\)
Exclude obs. missing on \(Y\)
Expand \(Y\) (spline or dummy variables)
Score (transform \(Y\)) using first canonical variate
Missing \(Y\) \(\rightarrow\) predict canonical variate from \(X\)s
The imputed values can optionally be shrunk to avoid overfitting for small \(n\) or large \(p\)
Constrain imputed values to be in range of non-imputed ones
Imputations on original scale
Multiple imputation — bootstrap or approx. Bayesian bootstrap.
fit.mult.impute works with aregImpute and transcan output to easily get imputation-corrected variances and avg. \(\hat{\beta}\)Option to insert constants as imputed values (ignored during transformation estimation); helpful when a lab value may be missing because the patient returned to normal
Imputations and transformed values may be easily obtained for new data
An R function Function will create a series of R functions that transform each predictor
Example: \(n=415\) acutely ill patients
Mean Arterial Blood Pressure Day 3
[1] 151 136Convergence criterion:2.901 0.035 0.007
Convergence in 4 iterations
R-squared achieved in predicting each variable:
heart.rate blood.pressure
0.259 0.259
Adjusted R-squared:
heart.rate blood.pressure
0.254 0.253 400 401
132.4057 109.7741 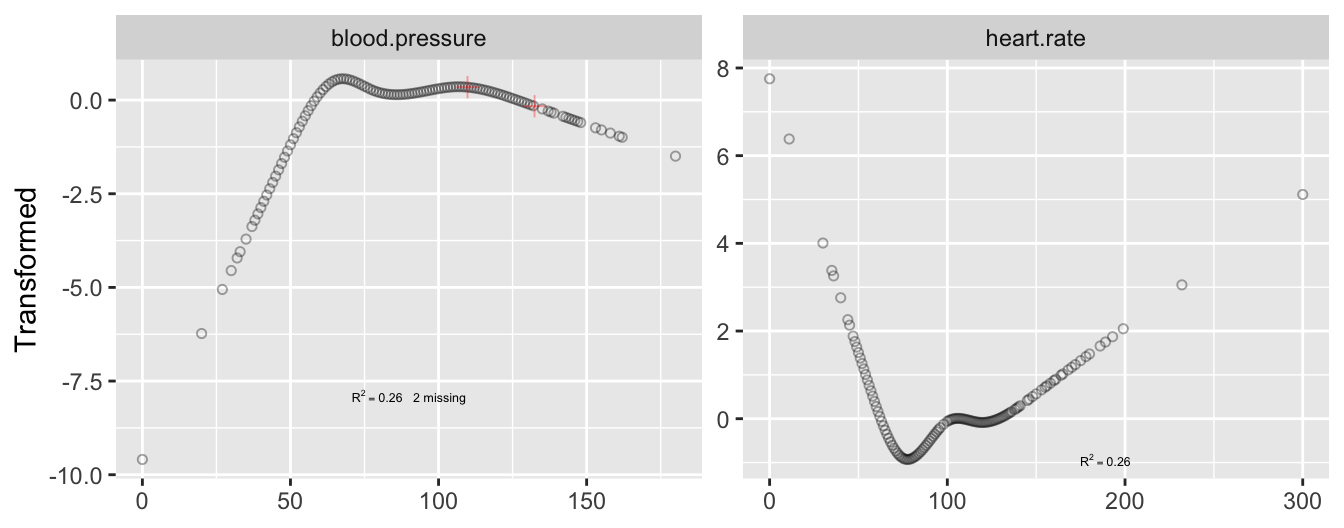
transcan. Tick marks indicate the two imputed values for blood pressure.
ACE (Alternating Conditional Expectation) of Breiman & Friedman (1985)
These methods find marginal transformations
Check adequacy of transformations using \(Y\)
Series of dichotomous variables:
Using Expected Shrinkage to Guide Data Reduction
Example:
| Goals | Reasons | Methods |
|---|---|---|
| Group predictors so that each group represents a single dimension that can be summarized with a single score | • \(\downarrow\) d.f. arising from multiple predictors • Make \(PC_1\) more reasonable summary |
Variable clustering • Subject matter knowledge • Group predictors to maximize proportion of variance explained by \(PC_1\) of each group • Hierarchical clustering using a matrix of similarity measures between predictors |
| Transform predictors | • \(\downarrow\) d.f. due to nonlinear and dummy variable components • Allows predictors to be optimally combined • Make \(PC_1\) more reasonable summary • Use in customized model for imputing missing values on each predictor |
• Maximum total variance on a group of related predictors • Canonical variates on the total set of predictors |
Reasons for influence:
Statistical Measures:
See also Section 5.6
Greenland (2000) discusses many important points:
Greenland’s example of inadequate adjustment for confounders as a result of using a bad modeling strategy:
Global Strategies
Preferred Strategy in a Nutshell
For an excellent tutorial covering many strategical aspects of developing and validating predictive models see Efthimiou et al. (2024).
Section 4.1
Section 4.3
Section 4.4
Section 4.5
Section 4.6
Section 4.7
Section 4.9
Section 4.10
Section 4.12
```{r include=FALSE}
options(qproject='rms', prType='html')
require(Hmisc)
require(qreport)
getRs('qbookfun.r')
hookaddcap()
knitr::set_alias(w = 'fig.width', h = 'fig.height', cap = 'fig.cap', scap ='fig.scap')
```
# Multivariable Modeling Strategies {#sec-multivar}
<!-- NEW -->
**Scientific Big Picture**[Thanks to Drew Levy for key contributions]{.aside}
* Rigorous judgements about information quality and sufficiency for explicit objectives should precede any modeling
+ Undertaking modeling and inference and subsequently apologizing for data deficiencies results in scientific noise
* Study design and measurement of key variables are $\frac{9}{10}$ of the problem
* Distinguish predictive vs. causitive effects of $X$
* Is the current sample size large enough to do an analysis whose goal is to find definitive answers that do not need to be independently validated?
+ In other words is $N$ large enough to submit a paper where the results of the analysis do not require external validation to be credible and actionable?
+ Near futility of analyses with $p > N$
* Poor quality data in abundant quantity are readily available
+ Data in sufficient quantity **and** quality are much less available
+ High quality data in sufficient quantity are rare
+ Be clear-eyed and honest about your data resources
* Is $N$ even large enough to do exploratory analyses?
* If $N$ is insufficient and you want to proceed, you must replace the unavailable data with assumptions or knowledge to make the _effective_ sample size adequate
+ All-or-nothing assumptions (how treatments and humans function, which variables are relevant, which variables have linear effects, which interactions are real, etc.), or
+ Informative Bayesian prior distributions
* See [On the uses and abuses of regression models](https://onlinelibrary.wiley.com/doi/10.1002/sim.10244) by JB Carlin and M Moreno-Betancur. See also [this](https://bsky.app/profile/georgheinze.bsky.social/post/3lsj4jzbghs2a).
<br>
**Modeling Strategy in a Nutshell**
`r mrg(sound("mv-1"))`
* "Spending d.f.": examining or fitting parameters in models, or `r ipacue()`
examining tables or graphs that utilize $Y$ to tell you how to
model variables
* If wish to preserve statistical properties, can't retrieve d.f.
once they are "spent" (see @gra91eff)
* If a scatterplot suggests linearity and you fit a linear model,
how many d.f. did you actually spend (i.e., the d.f. that when put
into a formula results in accurate confidence limits or $P$-values)?
----
* Decide number of d.f. that can be spent `r ipacue()`
* Decide where to spend them
* Spend them
* General references: [@nic99reg; @ste01pro; @har96mul; @giu11spe]
----
There are many choices to be made when deciding upon a global modeling
strategy, including choice between
* parametric and nonparametric procedures `r ipacue()`
* parsimony and complexity
* parsimony and good discrimination ability
* interpretable models and black boxes.
## Prespecification of Predictor Complexity Without Later Simplification {#sec-multivar-complexity}
`r mrg(sound("mv-2"))`
* Rarely expect linearity `r ipacue()`
* Can't always use graphs or other devices to choose
transformation
* If select from among many transformations, results biased
* Need to allow flexible nonlinearity to potentially strong
predictors not _known_ to predict linearly
* Once decide a predictor is "in" can choose no. of
parameters to devote to it using a general association index
with $Y$
* Need a measure of "potential predictive punch"
* Measure needs to mask analyst to true form of regression to
preserve statistical properties
Motivating examples:
```{r tradeoffs,h=6,w=6}
#| label: fig-multivar-fitting-errors
#| fig-cap: "Fitting errors to withstand or to avoid"
# Overfitting a flat relationship
require(rms)
set.seed(1)
x <- runif(1000)
y <- runif(1000, -0.5, 0.5)
dd <- datadist(x, y); options(datadist='dd')
par(mfrow=c(2,2), mar=c(2, 2, 3, 0.5))
pp <- function(actual) {
yhat <- predict(f, data.frame(x=xs))
yreal <- actual(xs)
plot(0, 0, xlim=c(0,1),
ylim=range(c(quantile(y, c(0.1, 0.9)), yhat,
yreal)),
type='n', axes=FALSE)
axis(1, labels=FALSE); axis(2, labels=FALSE)
lines(xs, yreal)
lines(xs, yhat, col='blue')
}
f <- ols(y ~ rcs(x, 5))
xs <- seq(0, 1, length=150)
pp(function(x) 0*x)
title('Mild Error:\nOverfitting a Flat Relationship',
cex=0.5)
y <- x + runif(1000, -0.5, 0.5)
f <- ols(y ~ rcs(x, 5))
pp(function(x) x)
title('Mild Error:\nOverfitting a Linear Relationship',
cex=0.5)
y <- x^4 + runif(1000, -1, 1)
f <- ols(y ~ x)
pp(function(x) x^4)
title('Serious Error:\nUnderfitting a Steep Relationship',
cex=0.5)
y <- - (x - 0.5) ^ 2 + runif(1000, -0.2, 0.2)
f <- ols(y ~ x)
pp(function(x) - (x - 0.5) ^ 2)
title('Tragic Error:\nMonotonic Fit to\nNon-Monotonic Relationship',
cex=0.5)
```
| | |
|----------|-----------|
| Categorical predictor with $k$ levels | Collapse less frequent categories into "other" |
| Continuous predictor represented as $k$-knot restricted cubic spline | Reduce $k$ to a number as low as 3, or 0 (linear) |
: Examples of Reducing the Number of Parameters
`r ipacue()`
### Learning From a Saturated Model
When the effective sample size available is sufficiently large so that
a saturated main effects model may be fitted, a good approach to
gauging predictive potential is the following.
* Let all continuous predictors be represented as restricted cubic `r ipacue()`
splines with $k$ knots, where $k$ is the maximum number of knots the
analyst entertains for the current problem.
* Let all categorical predictors retain their original categories
except for pooling of very low prevalence categories (e.g., ones
containing $<6$ observations).
* Fit this general main effects model.
* Compute the partial $\chi^2$ statistic for testing the
association of each predictor with the response, adjusted for all
other predictors. In the case of ordinary regression convert
partial $F$ statistics to $\chi^2$ statistics or partial $R^2$
values.
* Make corrections for chance associations to "level the playing
field" for predictors having greatly varying d.f., e.g., subtract
the d.f. from the partial $\chi^2$ (the expected value of
$\chi^{2}_{p}$ is $p$ under $H_{0}$).
* Make certain that tests of nonlinearity are not revealed as this
would bias the analyst.
* Sort the partial association statistics in descending order.
Commands in the `rms` package can be used to plot only what is
needed. Here is an example for a logistic model.
```{r eval=FALSE}
f <- lrm(y ~ sex + race + rcs(age,5) + rcs(weight,5) +
rcs(height,5) + rcs(blood.pressure,5))
plot(anova(f))
```
### Using Marginal Generalized Rank Correlations
When collinearities or confounding are not problematic, a quicker
approach based on pairwise measures of association can be useful.
This approach will not have numerical problems (e.g., singular
covariance matrix) and is based on:
* 2 d.f. generalization of Spearman $\rho$---$R^2$ based on `r ipacue()`
$rank(X)$ and $rank(X)^2$ vs. $rank(Y)$
* $\rho^2$ can detect U-shaped relationships
* For categorical $X$, $\rho^2$ is $R^2$ from dummy variables
regressed against $rank(Y)$; this is tightly related to the
Wilcoxon-Mann-Whitney-Kruskal-Wallis rank test for group
differences^[This test statistic does not inform the analyst of _which_ groups are different from one another.]
* Sort variables by descending order of $\rho^2$
* Specify number of knots for continuous $X$, combine infrequent
categories of categorical $X$ based on $\rho^2$
Allocating d.f. based on partial tests of association or sorting
$\rho^2$ is a fair procedure because
* We already decided to keep variable in model no matter what `r ipacue()`
$\rho^2$ or $\chi^2$ values are seen
* $\rho^2$ and $\chi^2$ do not reveal degree of nonlinearity;
high value may be due solely to strong linear effect
* low $\rho^2$ or $\chi^2$ for a categorical variable might lead to
collapsing the most disparate categories
Initial simulations show the procedure to be conservative. Note that
one can move from simpler to more complex models but not the other
way round
## Checking Assumptions of Multiple Predictors Simultaneously
* Sometimes failure to adjust for other variables gives wrong `r ipacue()`
transformation of an $X$, or wrong significance of interactions
* Sometimes unwieldy to deal simultaneously with all predictors
at each stage $\rightarrow$ assess regression assumptions separately
for each predictor
## Variable Selection {#sec-multivar-variable-selection}
`r mrg(sound("mv-3"))`
* Series of potential predictors with no prior knowledge `r ipacue()`
* $\uparrow$ exploration $\rightarrow$ $\uparrow$ shrinkage (overfitting)
* Summary of problem: $E(\hat{\beta} | \hat{\beta}$
"significant" $) \neq \beta$ [@cha95mod]
* Biased $R^2$, $\hat{\beta}$, standard errors, $P$-values too small
* $F$ and $\chi^2$ statistics do not have the claimed
distribution^[@loc13sig provide an example with $n=100$ and 10 orthogonal predictors where all true $\beta$s are zero. The test statistic for the first variable to enter has type I assertion probability of 0.39 when the nominal $\alpha$ is set to 0.05.] [@gra91eff]
* Will result in residual confounding if use variable selection
to find confounders [@gre00whe]
* @der92bac found that in stepwise analyses the final model represented noise 0.20-0.74 of time, final model usually contained $< \frac{1}{2}$ actual number of authentic predictors. Also: `r ipacue()`
>> 1. The degree of correlation between the predictor variables affected
the frequency with which authentic predictor variables found their way
into the final model.
>> 2. The number of candidate predictor variables affected the number of
noise variables that gained entry to the model.
>> 3. The size of the sample was of little practical importance in
determining the number of authentic variables contained in the final
model.
>> 4. The population multiple coefficient of determination could be
faithfully estimated by adopting a statistic that is adjusted by
the total number of candidate predictor variables rather than the
number of variables in the final model.
* Global test with $p$ d.f. insignificant $\rightarrow$ **stop**
Simulation experiment, true $\sigma^{2} = 6.25$, 8 candidate `r ipacue()`
variables, 4 of them related to $Y$ in the population. Select best
model using all possible subsets regression to maximize $R^{2}_{adj}$ (all possible subsets is not usually recommended but gives variable selection more of a chance to work in this context).
`r mrg(sound("mv-4"))`
**Note**: The audio was made using stepAIC with collinearities in predictors. The code below allows for several options. Here we use all possible subsets of predictors and force predictors to be uncorrelated, which is the easiest case for variable selection.
```{r}
require(MASS) # provides stepAIC function
require(leaps) # provides regsubsets function
sim <- function(n, sigma=2.5, method=c('stepaic', 'leaps'),
pr=FALSE, prcor=FALSE, dataonly=FALSE) {
method <- match.arg(method)
if(uncorrelated) {
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- rnorm(n)
x5 <- rnorm(n)
x6 <- rnorm(n)
x7 <- rnorm(n)
x8 <- rnorm(n)
}
else {
x1 <- rnorm(n)
x2 <- x1 + 2.0 * rnorm(n) # was + 0.5 * rnorm(n)
x3 <- rnorm(n)
x4 <- x3 + 1.5 * rnorm(n)
x5 <- x1 + rnorm(n)/1.3
x6 <- x2 + 2.25 * rnorm(n) # was rnorm(n)/1.3
x7 <- x3 + x4 + 2.5 * rnorm(n) # was + rnorm(n)
x8 <- x7 + 4.0 * rnorm(n) # was + 0.5 * rnorm(n)
}
z <- cbind(x1,x2,x3,x4,x5,x6,x7,x8)
if(prcor) return(round(cor(z), 2))
lp <- x1 + x2 + .5*x3 + .4*x7
y <- lp + sigma*rnorm(n)
if(dataonly) return(list(x=z, y=y))
if(method == 'leaps') {
s <- summary(regsubsets(z, y))
best <- which.max(s$adjr2)
xvars <- s$which[best, -1] # remove intercept
ssr <- s$rss[best]
p <- sum(xvars)
xs <- if(p == 0) 'none' else paste((1 : 8)[xvars], collapse='')
if(pr) print(xs)
ssesw <- (n - 1) * var(y) - ssr
s2s <- ssesw / (n - p - 1)
yhat <- if(p == 0) mean(y) else fitted(lm(y ~ z[, xvars]))
}
f <- lm(y ~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8)
if(method == 'stepaic') {
g <- stepAIC(f, trace=0)
p <- g$rank - 1
xs <- if(p == 0) 'none' else
gsub('[ <br>+x]','', as.character(formula(g))[3])
if(pr) print(formula(g), showEnv=FALSE)
ssesw <- sum(resid(g)^2)
s2s <- ssesw/g$df.residual
yhat <- fitted(g)
}
# Set SSEsw / (n - gdf - 1) = true sigma^2
gdf <- n - 1 - ssesw / (sigma^2)
# Compute root mean squared error against true linear predictor
rmse.full <- sqrt(mean((fitted(f) - lp) ^ 2))
rmse.step <- sqrt(mean((yhat - lp) ^ 2))
list(stats=c(n=n, vratio=s2s/(sigma^2),
gdf=gdf, apparentdf=p, rmse.full=rmse.full, rmse.step=rmse.step),
xselected=xs)
}
rsim <- function(B, n, method=c('stepaic', 'leaps')) {
method <- match.arg(method)
xs <- character(B)
r <- matrix(NA, nrow=B, ncol=6)
for(i in 1:B) {
w <- sim(n, method=method)
r[i,] <- w$stats
xs[i] <- w$xselected
}
colnames(r) <- names(w$stats)
s <- apply(r, 2, median)
p <- r[, 'apparentdf']
s['apparentdf'] <- mean(p)
print(round(s, 2))
print(table(p))
cat('Prob[correct model]=', round(sum(xs == '1237')/B, 2), '\n')
}
```
Show the correlation matrix being assumed for the $X$s:
```{r}
uncorrelated <- TRUE
sim(50000, prcor=TRUE)
```
Simulate to find the distribution of the number of variables selected, `r ipacue()`
the proportion of simulations in which the true model ($X_{1}, X_{2},
X_{3}, X_{7}$) was found, the median value of
$\hat{\sigma}^{2}/\sigma^{2}$, the median effective d.f., and the mean
number of apparent d.f., for varying sample sizes.
```{r cache=FALSE}
set.seed(11)
m <- 'leaps' # all possible regressions stopping on R2adj
rsim(100, 20, method=m) # actual model found twice out of 100
rsim(100, 40, method=m)
rsim(100, 150, method=m)
rsim(100, 300, method=m)
rsim(100, 2000)
```
As $n\uparrow$ the mean number of variables selected increased. The
proportion of simulations in which the correct model was found
increased from 0 to 0.53. $\sigma^{2}$ is underestimated when $n=300$ by a factor of 0.42, resulting in the d.f. needed to de-bias
$\hat{\sigma^{2}}$ being greater than $n$ when the apparent d.f. was only 5.16 on
the average. Variable selection slightly increased closeness
to the true $X\beta$.
If the simulations are re-run allowing for collinearities (`uncorrelated=FALSE`) one can expect variable selection to be even more problematic.
Variable selection methods [@logist]:
`r mrg(sound("mv-5"))`
* Forward selection, backward elimination `r ipacue()`
* Stopping rule: "residual $\chi^{2}$" with d.f. = no.
candidates remaining at current step
* Test for significance or use Akaike's information criterion
(AIC [@atk80not]), here $\chi^{2}-2 \times d.f.$
* Better to use subject matter knowledge!
* No currently available stopping rule was developed for
stepwise, only for comparing a limited number of pre-specified
models[@bre92lit, Section 1.3]
* @roe91pre studied forward selection (FS), all `r ipacue()`
possible subsets selection (APS), full fits
* APS more likely to select smaller, less accurate models than FS
* Neither as accurate as full model fit unless more than half of
candidate variables redundant or unnecessary
* Step-down is usually better than forward [@man70why] and can
be used efficiently with maximum likelihood
estimation [@law78eff]
* Fruitless to try different stepwise methods to look for
agreement [@wie10per]
* Bootstrap can help decide between full and reduced model `r ipacue()`
* Full model fits gives meaningful confidence intervals with
standard formulas, C.I. after stepwise does
not [@alt89boo; @hur90imp; @bre92lit]
* Data reduction (grouping variables) can help
* Using the bootstrap to select important variables
for inclusion in the final model [@sau92boo] is
problematic [@aus08boo]
* It is not logical that a population regression coefficient
would be exactly zero just because its estimate was "insignificant"
See also these articles:
* [Step away from stepwise](https://journalofbigdata.springeropen.com/articles/10.1186/s40537-018-0143-6) by Gary Smith `r ipacue()`
* [Five myths about variable selection](https://onlinelibrary.wiley.com/doi/full/10.1111/tri.12895) by Georg Heinze and Daniela Dunkler
* [Variable selection - A review and recommendations for the practicing statistician](https://onlinelibrary.wiley.com/doi/full/10.1002/bimj.201700067) by Georg Heinze, Christine Wallisch, Daniela Dunkler
* [Stopping stepwise](https://towardsdatascience.com/stopping-stepwise-why-stepwise-selection-is-bad-and-what-you-should-use-instead-90818b3f52df) by Peter Flom
* [Best subset, forward stepwise or lasso? Analysis and recommendations based on extensive simulations](https://www.stat.cmu.edu/~ryantibs/papers/bestsubset-sts.pdf) by Trevor Hastie, Robert Tibshirani, and Ryan Tibshirani, 2020
* [Variable selection results in worse predictions than general shrinkage such as ridge regression](https://stats.stackexchange.com/a/669294/4253)
### Maxwell's Demon as an Analogy to Variable Selection
`r mrg(sound("mv-5a"))`
Some of the information in the data is spent on variable selection
instead of using all information for estimation.
Model _specification_ is preferred to model _selection_.
Information content of the data usually insufficient for reliable
variable selection.
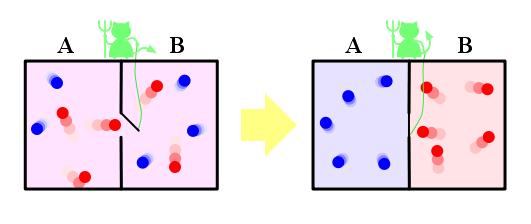
<img src="images/maxwellsdemon.jpg" width="65%"> <img src="images/maxwell.jpg" width="25%">[James Clerk Maxwell]{.aside}
<small>Maxwell imagines one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other. Observing the molecules on both sides, an imaginary demon guards a trapdoor between the two parts. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. Likewise, when a slower-than-average molecule from B flies towards the trapdoor, the demon will let it pass from B to A. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics. </small>
Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy. Since the demon and the gas are interacting, we must consider the total entropy of the gas and the demon combined. The expenditure of energy by the demon will cause an increase in the entropy of the demon, which will be larger than the lowering of the entropy of the gas.
Source: [commons.wikimedia.org/wiki/File:YoungJamesClerkMaxwell.jpg](commons.wikimedia.org/wiki/File:YoungJamesClerkMaxwell.jpg)<br>
[en.wikipedia.org/wiki/Maxwell's_demon](en.wikipedia.org/wiki/Maxwell's_demon)
Peter Ellis' [blog article](https://ellisp.github.io/blog/2017/03/12/stepwise-timeseries) contains excellent examples of issues
discussed here but applied to time series modeling.
## Overfitting and Limits on Number of Predictors {#sec-multivar-overfit}
`r mrg(sound("mv-6"))`
* Concerned with avoiding overfitting `r ipacue()`
* Assume typical problem in medicine, epidemiology, and the
social sciences in which the signal:noise ratio is small (higher
ratios allow for more aggressive modeling)
* $p$ should be $< \frac{m}{15}$ [@har84reg; @har85reg; @smi92pro; @ped95imp; @ped96sim; @vit06rel; @plo14mod]
* $p$ is number of parameters in full model or number of _candidate_
parameters in a stepwise analysis, and $m$ is the effective sample size
+ See @sec-ordsurv for how to estimate the effective sample size coming from censored observations
* Derived from simulations to find minimum sample size so that
apparent discrimination = validated discrimination
* Applies to typical signal:noise ratios found outside of tightly
controlled experiments
* If true $R^{2}$ is high, many parameters can be estimated from
smaller samples
* Ignores sample size needed just to estimate the intercept or, in semiparametric models, the underlying distribution function^[The sample size needed for these is model-dependent]
* @ril19min and @ril19mina have refined sample size
estimation for continuous, binary, and time-to-event models to
account for all of these issues
* See also [Riley et al](https://arxiv.org/abs/2504.18730) 2025
* To just estimate $\sigma$ in a linear model with a multiplicative margin of error of 1.2 with 0.95 confidence requires $n=70$
* See [this](https://stats.stackexchange.com/questions/10079) for an excellent discussion of the sample size needed for ordinary linear models
<!-- NEW changed eff sample size for binary -->
`r fa <- '^[If one considers the power of a two-sample binomial test compared with a Wilcoxon test if the response could be made continuous and the proportional odds assumption holds, the effective sample size for a binary response is $3 n_{1}n_{2}/n \\approx 3 \\min(n_{1}, n_{2})$ if $\\frac{n_{1}}{n}$ is near 0 or 1 [@whi93sam, Eq. 10, 15]. Here $n_{1}$ and $n_{2}$ are the marginal frequencies of the two response levels [@ped96sim]. The effective sample size is a maximum ($0.75n$) when $n_{1}=n_{2}$, i.e. $q=\\frac{1}{2}$ .]'`
`r fb <- '^[Based on the power of a proportional odds model two-sample test when the marginal cell sizes for the response are $n_{1}, \\ldots, n_{k}$, compared with all cell sizes equal to unity (response is continuous) [@whi93sam, Eq. 3]. If all cell sizes are equal, the relative efficiency of having $k$ response categories compared to a continuous response is $1 - \\frac{1}{k^{2}}$ [@whi93sam, Eq. 14], e.g., a 5-level response is almost as efficient as a continuous one if proportional odds holds across category cutoffs.]'`
`r fc <- '^[This is approximate, as the effective sample size may sometimes be boosted somewhat by censored observations, especially for non-proportional hazards methods such as Wilcoxon-type tests [@ben82eff].]'`
`r ipacue()`
| Type of Response Variable | Limiting Sample Size $m$ |
|-----|-----|
| Continuous | $n$ (total sample size) |
| Binary | $3nq(1-q), q=\frac{n_{2}}{n}$ `r fa` |
| Ordinal ($k$ categories) | $n - \frac{1}{n^{2}} \sum_{i=1}^{k} n_{i}^{3}$ `r fb` |
| Failure (survival) time | number of failures `r fc` |
: Limiting Sample Sizes for Various Response Variable Types
* Narrowly distributed predictor $\rightarrow$ even higher $n$ `r ipacue()`[See [this](https://stats.stackexchange.com/questions/655891) and [this](https://hbiostat.org/R/glossary.html) for more information.]{.aside}
* $p$ includes _all_ variables screened for association
with response, including interactions
* Univariable screening (graphs, crosstabs, etc.) **in no way**
reduces multiple comparison problems of model building [@sun96ina]
<!-- NEW -->
::: {.callout-note collapse="true"}
## More About the Binary $Y$ Case
To derive the effective sample size for binary $Y$ we compare two samples of equal size $\frac{n}{2}$ by testing whether the log odds ratio is zero. When the two samples come from populations with equal $\Pr(Y=1) = q$, the variance of the log odds ratio is approximately $2 \times \frac{1}{\frac{n}{2}q(1-q)} = \frac{4}{nq(1-q)}$. When $Y$ is continuous with no ties and a Wilcoxon or proportional odds model test is used, the reciprocal of the variance of the proportional odds model's log odds ratio is $\frac{n^{3}}{12 (n+1)^{2}} \times (1 - \frac{1}{n^{2}}) \approx \frac{n}{12}$ so the variance is approximately $\frac{12}{n}$. The ratio of this to the binary $Y$ variance is $3q(1-q)$.
:::
## Shrinkage {#sec-multivar-est-use-shrink}
`r mrg(movie("https://youtu.be/yWoKLDy8IQA"), sound("mv-7"))`
* Slope of calibration plot; regression to the mean `r ipacue()`
* Statistical estimation procedure --- "pre-shrunk" models
* Aren't regression coefficients OK because they're unbiased?
* Problem is in how we use coefficient estimates
* Consider 20 samples of size $n=50$ from $U(0,1)$
* Compute group means and plot in ascending order
* Equivalent to fitting an intercept and 19 dummies using least
squares
* Result generalizes to general problems in plotting $Y$ vs.\
$X\hat{\beta}$
```{r ps=7,cap='Sorted means from 20 samples of size 50 from a uniform $[0,1]$ distribution. The reference line at 0.5 depicts the true population value of all of the means.',scap='Means from 20 $U(0,1)$ samples'}
#| label: fig-multivar-shrink-groupmeans
set.seed(123)
n <- 50
y <- runif(20*n)
group <- rep(1:20,each=n)
ybar <- tapply(y, group, mean)
ybar <- sort(ybar)
plot(1:20, ybar, type='n', axes=FALSE, ylim=c(.3,.7),
xlab='Group', ylab='Group Mean')
lines(1:20, ybar)
points(1:20, ybar, pch=20, cex=.5)
axis(2)
axis(1, at=1:20, labels=FALSE)
for(j in 1:20) axis(1, at=j, labels=names(ybar)[j])
```
* Prevent shrinkage by using pre-shrinkage `r ipacue()`
* @spi86pro: var. selection arbitrary, better
prediction usually results from fitting all candidate
variables and using shrinkage
* Shrinkage closer to that expected from full model fit than based on
number of significant variables [@cop83reg]
* Ridge regression [@ces92rid; @hou90pre]
* Penalized MLE [@ver94pen; @gra92fle; @har98dev]
* Heuristic shrinkage parameter of van Houwelingen and le `r ipacue()`
Cessie [@hou90pre, Eq. 77]
$$\hat{\gamma} = \frac{{\rm model}\ \chi^{2} - p}{{\rm model}\ \chi^{2}},$$ {#eq-heuristic-shrink}
* OLS^[An excellent discussion about such indexes may be found [here](https://stats.stackexchange.com/questions/48703).]:
$\hat{\gamma} = \frac{n-p-1}{n-1} R^{2}_{\rm adj} / R^{2}$ <br>
$R^{2}_{\rm adj} = 1 - (1 - R^{2})\frac{n-1}{n-p-1}$
* $p$ close to no. candidate variables
* @cop83reg (Eq. 8.5) adds 2 to numerator
## Collinearity {#sec-multivar-collinear}
`r mrg(sound("mv-8"))`
* When at least 1 predictor can be predicted well from others `r ipacue()`
* Can be a blessing (data reduction, transformations)
* $\uparrow$ s.e. of $\hat{\beta}$, $\downarrow$ power
* This is appropriate $\rightarrow$ asking too much of the
data [@cha12reg, Chap. 9]
* Variables compete in variable selection, chosen one
arbitrary
* Does not affect joint influence of a set of highly correlated
variables (use multiple d.f. tests)
* Does not harm predictions on model construction
sample `r ipacue()`
* Does not affect predictions on new data [@mye90cla, pp. 379-381] if
+ Extreme extrapolation not attempted
+ New data have same type of collinearities as original data
* Example: LDL and total cholesterol -- problem only if more inconsistent
in new data
* Example: age and age$^{2}$ -- no problem
* One way to quantify for each predictor:
variance inflation factors (VIF)
* General approach (maximum likelihood) --- transform information
matrix to correlation form, VIF=diagonal of
inverse [@dav86exa; @wax92col]
* See @bel91con, pp. 28-30 for problems with VIF
* Easy approach: SAS `VARCLUS` procedure [@varclus], `r ipacue()`
`R` `varclus` function,
other clustering techniques: group highly correlated variables
* Can score each group (e.g., first principal component,
$PC_1$ [@dag95dev]); summary scores not collinear
## Data Reduction {#sec-multivar-data-reduction}
`r mrg(sound("mv-9"))`
* Unless $n>>p$, model unlikely to validate `r ipacue()`
* Data reduction: $\downarrow p$
* Use the literature to eliminate unimportant variables.
* Eliminate variables whose distributions are too narrow.
* Eliminate candidate predictors that are missing in a large
number of subjects, especially if those same predictors are likely
to be missing for future applications of the model.
* Use a statistical data reduction method such as incomplete
principal components regression, nonlinear
generalizations of principal components such as principal surfaces,
sliced inverse regression, variable clustering,
or ordinary cluster analysis on a measure of similarity
between variables.
* Data reduction is **completely masked to $Y$**, which is precisely why it does not distort estimates, standard errors, $P$-values, or confidence limits
* Data reduction = _unsupervised learning_
* Example: dataset with 40 events and 60 candidate predictors
+ Use variable clustering to group variables by correlation structure
+ Use clinical knowledge to refine the clusters
+ Keep age and severity of disease as separate predictors because of their strength
+ For others create clusters: socioeconomic, risk factors/history, and physiologic function
+ Summarize each cluster with its first principal component $PC_{1}$, i.e., the linear combination of characteristics that maximizes variance of the score across subjects subject to an overall constraint on the coefficients
+ Fit outcome model with 5 predictors
* See [this](https://stats.stackexchange.com/questions/5774) [this](https://stats.stackexchange.com/questions/547566) and [this](https://stats.stackexchange.com/questions/3810) for useful resources related to principal component analysis of mixed continuous and categorical variables
* [Multivariate analysis of mixed data: The R package PCAmixdata](https://arxiv.org/abs/1411.4911) by M Chavent et al, 2022.
* R [homals package](https://cran.r-project.org/web/packages/homals)
* See [this](https://stats.stackexchange.com/questions/239898) for an excellent discussion of whether data reduction (unsupervised learning) steps need to be included in resampling for model validation
### Redundancy Analysis {#sec-multivar-redun}
* Remove variables that have poor distributions `r ipacue()`
+ E.g., categorical variables with fewer than 2 categories having
at least 20 observations
* Use flexible additive parametric models to
determine how well each variable can be predicted from the remaining
variables
* Variables dropped in stepwise fashion, removing the
most predictable variable at each step
* Remaining variables used to predict
* Process continues until no variable still in the list
of predictors can be predicted with an $R^2$ or adjusted $R^2$ greater
than a specified threshold or until dropping the variable with the highest
$R^2$ (adjusted or ordinary) would cause a variable that was dropped
earlier to no longer be predicted at the threshold from
the now smaller list of predictors
* `R` function `redun` in `Hmisc` package
* Related to _principal variables_ [@mcc84pri] but faster
### Variable Clustering
* Goal: Separate variables into groups `r ipacue()`
+ variables within group correlated with each other
+ variables not correlated with non-group members
* Score each dimension, stop trying to separate effects of
factors measuring same phenomenon
* Variable clustering [@varclus; @dag95dev] (oblique-rotation PC analysis) $\rightarrow$
separate variables so that first PC is representative of group
* Can also do hierarchical cluster analysis on similarity matrix
based on squared Spearman or Pearson correlations, or more
generally, Hoeffding's $D$ [@hoe48non].
* See @guo11pri for a method related to variable clustering
and sparse principal components.
* @cha12clu implement many more variable clustering methods
Example: @fig-cony-redun
### Transformation and Scaling Variables Without Using $Y$
`r mrg(sound("mv-9a"))`
* Reduce $p$ by estimating transformations using associations `r ipacue()`
with other predictors
* Purely categorical predictors -- correspondence
analysis [@lec88cor; @cri89cor; @cia86str; @gre88cor; @mic98gif]
* Mixture of qualitative and continuous variables: qualitative
principal components
* Maximum total variance (MTV) of Young, Takane, de
Leeuw [@you78pri; @mic98gif]
1. Compute $PC_1$ of variables using correlation matrix
1. Use regression (with splines, dummies, etc.) to predict
$PC_1$ from each $X$ --- expand each $X_j$ and regress
it separately on $PC_1$ to get working transformations
1. Recompute $PC_1$ on transformed $X$s
1. Repeat 3-4 times until variation explained by $PC_1$
plateaus and transformations stabilize
* Maximum generalized variance (MGV) method of
Sarle [@prinqual, pp. 1267-1268]
1. Predict each variable from (current transformations of)
all other variables
1. For each variable, expand it into linear and nonlinear
terms or dummies, compute first canonical variate
1. For example, if there are only two variables $X_{1}$ and
$X_{2}$ represented as quadratic polynomials, solve for
$a,b,c,d$ such that
$aX_{1}+bX_{1}^{2}$ has maximum correlation with
$cX_{2}+dX_{2}^{2}$.
1. Goal is to transform each var. so that it is most similar
to predictions from other transformed variables
1. Does not rely on PCs or variable clustering
* MTV (PC-based instead of canonical var.)
and MGV implemented in SAS `PROC PRINQUAL` [@prinqual]
1. Allows flexible transformations including monotonic splines
1. Does not allow restricted cubic splines, so may be unstable unless
monotonicity assumed
1. Allows simultaneous imputation but often yields wild estimates
### Simultaneous Transformation and Imputation {#sec-multivar-trans-impute}
`R` `transcan` Function for Data Reduction & Imputation
* Initialize missings to medians (or most frequent category) `r ipacue()`
* Initialize transformations to original variables
* Take each variable in turn as $Y$
* Exclude obs. missing on $Y$
* Expand $Y$ (spline or dummy variables)
* Score (transform $Y$) using first canonical variate
* Missing $Y$ $\rightarrow$ predict canonical variate from $X$s
* The imputed values can optionally be shrunk to avoid
overfitting for small $n$ or large $p$
* Constrain imputed values to be in range of non-imputed ones
* Imputations on original scale
+ Continuous $\rightarrow$ back-solve with linear interpolation
+ Categorical $\rightarrow$ classification tree (most freq. cat.) or
match to category whose canonical score is closest
to one predicted
* Multiple imputation --- bootstrap or approx. Bayesian bootstrap.
+ Sample residuals multiple times (default $M=5$)
+ Are on "optimally" transformed scale
+ Back-transform
+ `fit.mult.impute` works with `aregImpute` and
`transcan` output to easily get imputation-corrected variances and
avg. $\hat{\beta}$
* Option to insert constants as imputed values (ignored during
transformation estimation); helpful when a lab value may
be missing because the patient returned to normal
* Imputations and transformed values may be easily
obtained for new data
* An `R` function `Function` will create a series of
`R` functions that transform each predictor
* Example: $n=415$ acutely ill patients
+ Relate heart rate to mean arterial blood pressure
+ Two blood pressures missing
+ Heart rate not monotonically related to blood pressure
+ See @fig-multivar-physiol-transcan and @fig-multivar-physiol-transcan2
<!-- NEW replaced plot with ggplot added trantab=TRUE -->
```{r cap='Transformations fitted using `transcan`. Tick marks indicate the two imputed values for blood pressure.',scap='`transcan` transformations for two physiologic variables'}
#| label: fig-multivar-physiol-transcan
#| fig-height: 2.75
require(Hmisc)
getHdata(support) # Get data frame from web site
heart.rate <- support$hrt
blood.pressure <- support$meanbp
blood.pressure[400:401]
blood.pressure[400:401] <- NA # Create two missings
d <- data.frame(heart.rate, blood.pressure)
w <- transcan(~ heart.rate + blood.pressure, transformed=TRUE,
imputed=TRUE, show.na=TRUE, data=d, trantab=TRUE, pl=FALSE)
ggplot(w)
w$imputed$blood.pressure
t <- w$transformed
spe <- round(c(spearman(heart.rate, blood.pressure),
spearman(t[,'heart.rate'],
t[,'blood.pressure'])), 2)
```
<!-- ??? TODO
#| fig-cap: !expr paste('Relationship between heart rate and blood pressure. The lower left plot contains raw data (Spearman $\\rho=',spe[1],'$); the lower right is a scatterplot of the corresponding transformed values ($\\rho=',spe[2],'$). Data courtesy of the SUPPORT study [@kna95sup].')
-->
`r this <- 'and that'`
```{r}
#| label: fig-multivar-physiol-transcan2
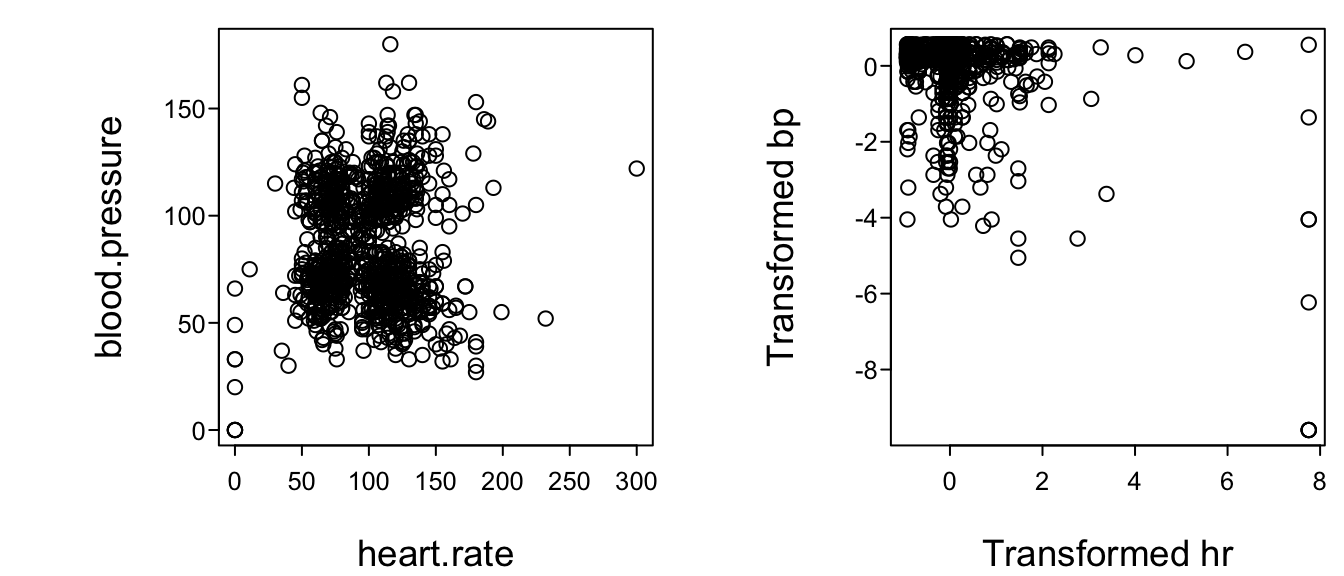
#| fig-cap: "Relationship between heart rate and blood pressure: untransformed data (left) and transformed data (right). Data courtesy of the SUPPORT study [@kna95sup]."
#| fig-scap: 'HR vs. BP before and after `transcan` transformations'
#| fig-height: 3
spar(mfrow=c(1,2))
plot(heart.rate, blood.pressure)
plot(t[,'heart.rate'], t[,'blood.pressure'],
xlab='Transformed hr', ylab='Transformed bp')
```
ACE (Alternating Conditional Expectation) of @bre85est
1. Uses nonparametric "super smoother" [@fri84var] `r ipacue()`
1. Allows monotonicity constraints, categorical vars.
1. Does not handle missing data
* These methods find _marginal_ transformations `r ipacue()`
* Check adequacy of transformations using $Y$
+ Graphical
+ Nonparametric smoothers ($X$ vs. $Y$)
+ Expand original variable using spline, test additional predictive information over original transformation
### Simple Scoring of Variable Clusters
`r mrg(sound("mv-10"))`
* Try to score groups of transformed variables with $PC_1$ `r ipacue()`
* Reduces d.f. by pre-transforming var. and by combining
multiple var.
* Later may want to break group apart, but delete all variables
in groups whose summary scores do not add significant information
* Sometimes simplify cluster score by finding a subset of its
constituent variables which predict it with high $R^2$.
Series of dichotomous variables:
* Construct $X_1$ = 0-1 according to whether any variables positive `r ipacue()`
* Construct $X_2$ = number of positives
* Test whether original variables add to $X_1$ or $X_2$
### Simplifying Cluster Scores
### How Much Data Reduction Is Necessary?
Using Expected Shrinkage to Guide Data Reduction
* Fit full model with all candidates, $p$ d.f., LR likelihood ratio `r ipacue()`
$\chi^2$
* Compute $\hat{\gamma}$
* If $<0.9$, consider shrunken estimator from whole model,
or data reduction (again not using $Y$)
* $q$ regression d.f. for reduced model
* Assume best case: discarded dimensions had no association with $Y$
* Expected loss in LR is $p-q$
* New shrinkage $[{\rm LR} - (p-q) - q]/[{\rm LR} - (p-q)]$
* Solve for $q$ $\rightarrow$ $q \leq ({\rm LR}-p)/9$
* Under these assumptions, no hope unless original LR $> p+9$
* No $\chi^2$ lost by dimension reduction $\rightarrow$ $q \leq {\rm LR}/10$
Example:
`r mrg(sound("mv-11"))`
* Binary logistic model, 45 events on 150 subjects `r ipacue()`
* 10:1 rule $\rightarrow$ analyze 4.5 d.f. total
* Analyst wishes to include age, sex, 10 others
* Not known if age linear or if age and sex additive
* 4 knots $\rightarrow$ $3+1+1$ d.f. for age and sex if
restrict interaction to be linear
* Full model with 15 d.f. has LR=50
* Expected shrinkage factor $(50-15)/50 = 0.7$
* LR$>15+9=24$ $\rightarrow$ reduction may help
* Reduction to $q = (50-15)/9 \approx 4$ d.f. necessary
* Have to assume age linear, reduce other 10 to 1 d.f.
* Separate hypothesis tests intended $\rightarrow$ use full model,
adjust for multiple comparisons
| Goals | Reasons | Methods |
|-------|---------|---------|
| Group predictors so that each group represents a single dimension that can be summarized with a single score | • $\downarrow$ d.f. arising from multiple predictors<br>• Make $PC_1$ more reasonable summary | Variable clustering<br><br>• Subject matter knowledge<br>• Group predictors to maximize proportion of variance explained by $PC_1$ of each group<br>• Hierarchical clustering using a matrix of similarity measures between predictors |
| Transform predictors | • $\downarrow$ d.f.\ due to nonlinear and dummy variable components<br>• Allows predictors to be optimally combined<br>• Make $PC_1$ more reasonable summary<br>• Use in customized model for imputing missing values on each predictor | • Maximum total variance on a group of related predictors<br>• Canonical variates on the total set of predictors |
: Summary of Some Data Reduction Methods
## Other Approaches to Predictive Modeling
## Overly Influential Observations {#sec-multivar-influence}
`r mrg(sound("mv-12"))`
* Every observation should influence fit `r ipacue()`
* Major results should not rest on 1 or 2 obs.
* Overly infl. obs. $\rightarrow$ $\uparrow$ variance of predictions
* Also affects variable selection
Reasons for influence:
* Too few observations for complexity of model (see @sec-multivar-data-reduction, @sec-multivar-variable-selection) `r ipacue()`
* Data transcription or entry errors
* Extreme values of a predictor
1. Sometimes subject so atypical should remove from dataset
1. Sometimes truncate measurements where data density ends
1. Example: $n=4000$, 2000 deaths, white blood count
range 500-100,000, .05,.95 quantiles=2755, 26700
1. Linear spline function fit
1. Sensitive to WBC$>60000\ (n=16)$
1. Predictions stable if truncate WBC to 40000 ($n=46$ above
40000)
* Disagreements between predictors and response. Ignore unless
extreme values or another explanation
* Example: $n=8000$, one extreme predictor value not on straight
line relationship with other $(X,Y)$ $\rightarrow$ $\chi^{2}=36$ for
$H_{0}:$ linearity
Statistical Measures:
* Leverage: capacity to be influential (not necessarily infl.) <br> `r ipacue()`
Diagonals of "hat matrix" $H = X(X'X)^{-1}X'$ --- measures how
an obs. predicts its own response [@bel80reg]
* $h_{ii}>2(p+1)/n$ may signal a high leverage
point [@bel80reg]
* DFBETAS: change in $\hat{\beta}$ upon deletion of each obs,
scaled by s.e.
* DFFIT: change in $X\hat{\beta}$ upon deletion of each obs
* DFFITS: DFFIT standardized by s.e. of $\hat{\beta}$
* Some classify obs as overly influential when
$|{\rm DFFITS}|>2\sqrt{(p+1)/(n-p-1)}$ [@bel80reg]
* Others examine entire distribution for "outliers"
* No substitute for careful examination of data [@cha91avo; @spe93rem]
* Maximum likelihood estimation requires 1-step approximations
## Comparing Two Models
`r mrg(sound("mv-13"))`
* Level playing field (independent datasets, same no. candidate `r ipacue()`
d.f., careful bootstrapping)
* Criteria:
1. calibration
1. discrimination
1. face validity
1. measurement errors in required predictors
1. use of continuous predictors (which are usually better defined
than categorical ones)
1. omission of "insignificant" variables that nonetheless make
sense as risk factors
1. simplicity (though this is less important with the
availability of computers)
1. lack of fit for specific types of subjects
* Goal is to rank-order: ignore calibration `r ipacue()`
* Otherwise, dismiss a model having poor calibration
* Good calibration $\rightarrow$ compare discrimination
(e.g., $R^{2}$ [@nag91not], model $\chi^2$,
Somers' $D_{xy}$, Spearman's $\rho$, area under ROC curve)
* Worthwhile to compare models on a measure not used to optimize `r ipacue()`
either model, e.g., mean absolute error, median absolute error if
using OLS
* Rank measures may not give enough credit to extreme predictions $\rightarrow$
model $\chi^{2}, R^{2}$, examine extremes of distribution of $\hat{Y}$
* Examine differences in predicted values from the two models
* See [@pee07ext; @pen08eva; @pen11ext; @pen12nov] for discussions
and examples of low power for testing differences in ROC areas, and
for other approaches.
## Improving the Practice of Multivariable Prediction
`r mrg(sound("mv-14"))`
See also @sec-val-habits
@gre00whe discusses many important points:
* Stepwise variable selection on confounders leaves important `r ipacue()`
confounders uncontrolled
* Shrinkage is far superior to variable selection
* Variable selection does more damage to confidence interval
widths than to point estimates
* Claims about unbiasedness of ordinary MLEs are misleading
because they assume the model is correct and is the only model
entertained
* "models need to be complex to capture uncertainty about the
relations ... an honest uncertainty assessment requires parameters
for all effects that we know may be present. This advice is
implicit in an anti-parsimony principle often attributed to
L. J. Savage 'All models should be as big as an elephant' (see Draper, 1995)"
Greenland's example of inadequate adjustment for confounders as a
result of using a bad modeling strategy:
* Case-control study of diet, food constituents, breast cancer `r ipacue()`
* 140 cases, 222 controls
* 35 food constituent intakes and 5 confounders
* Food intakes are correlated
* Traditional stepwise analysis not adjusting simultaneously
for all foods consumed $\rightarrow$ 11 foods had $P < 0.05$
* Full model with all 35 foods competing $\rightarrow$ 2 had $P < 0.05$
* Rigorous simultaneous analysis (hierarchical random slopes
model) penalizing estimates for the number of associations
examined $\rightarrow$ no foods associated with breast cancer
**Global Strategies**
* Use a method known not to work well (e.g., stepwise variable `r ipacue()`
selection without penalization; recursive partitioning), document
how poorly the model
performs (e.g. using the bootstrap), and use the model anyway
* Develop a black box model that performs poorly and is difficult
to interpret (e.g., does not incorporate penalization)
* Develop a black box model that performs well and is difficult to interpret
* Develop interpretable approximations to the black box
* Develop an interpretable model (e.g. give priority to additive
effects) that performs well and is likely to perform equally well
on future data from the same stream
**Preferred Strategy in a Nutshell**
* Decide how many d.f. can be spent `r ipacue()`
* Decide where to spend them
* Spend them
* Don't reconsider, especially if inference needed
## Summary: Possible Modeling Strategies {#sec-multivar-strategy}
### Developing Predictive Models
`r mrg(sound("mv-15"))`
For an excellent tutorial covering many strategical aspects of developing and validating predictive models see @eft24dev.
1. Assemble accurate, pertinent data and lots of it, with wide `r ipacue()`
distributions for $X$.
1. Formulate good hypotheses --- specify
relevant candidate predictors and possible interactions. Don't
use $Y$ to decide which $X$'s to include.
1. Characterize subjects with missing $Y$. Delete such subjects
only in rare circumstances [@cra95com]. For certain models it
is effective to multiply impute $Y$.
1. Characterize and impute missing $X$. In most cases use
multiple imputation based on $X$ and $Y$
1. For each predictor specify complexity or degree of
nonlinearity that should be allowed (more for important
predictors or for large $n$) (@sec-multivar-complexity)
1. Do data reduction if needed (pre-transformations, combinations),
or use penalized estimation [@har98dev]
1. Use the entire sample in model development unless $n$ is very large
1. Can do highly structured testing to simplify "initial" model
+ Test entire group of predictors with a single $P$-value
+ Make each continuous predictor have same number of knots,
and select the number that optimizes AIC
+ Test the combined effects of all nonlinear terms with a
single $P$-value
1. Make tests of linearity of effects in the model only to
demonstrate to others that such effects are often statistically
significant. Don't remove individual insignificant effects from the model.
1. Check additivity assumptions by testing pre-specified
interaction terms. Use a global test and either keep all or
delete all interactions.
1. Check to see if there are overly-influential observations.
1. Check distributional assumptions and choose a different model
if needed.
1. Do limited backwards step-down variable selection if parsimony
is more important that accuracy [@spi86pro]. But confidence
limits, etc., must account for variable selection (e.g., bootstrap).
1. This is the "final" model.
1. Interpret the model graphically and by computing predicted
values and appropriate test statistics. Compute pooled tests of
association for collinear predictors.
1. Validate this model for calibration and discrimination ability,
preferably using bootstrapping.
1. Shrink parameter estimates if there is overfitting but no
further data reduction is desired (unless shrinkage built-in to
estimation)
1. When missing values were imputed, adjust final
variance-covariance matrix
for imputation. Do this as early as possible because
it will affect other findings.
1. When all steps of the modeling strategy can be automated,
consider using @far92cos to penalize for
the randomness inherent in the multiple steps.
1. Develop simplifications to the final model as needed.
<!-- NEW confounding 2023-05-30 -->
### Developing Models for Effect Estimation
`r mrg(sound("mv-16"))`
1. Less need for parsimony; even less need to remove insignificant `r ipacue()`
variables from model (otherwise CLs too narrow)
1. Careful consideration of interactions; inclusion forces
estimates to be conditional and raises variances
1. If variable of interest is mostly the one that is missing,
multiple imputation less valuable
1. Complexity of main variable specified by prior beliefs,
compromise between variance and bias
1. Don't penalize terms for variable of interest
1. Model validation less necessary
1. Like the hypothesis testing scenario covered next, when one is attempting to apply a causal interpretation to the effect being estimated, consideration of pathways and confounding are all-important. Collider bias and backdoor pathways can ruin interpretation, and so can the omission of confounder variables that would have provided alternate explanations for observed effects of interest. In pure prediction mode we don't care very much how we got here, but in isolating the effect of a specific variable in the model, e.g., in estimating the effect of treatment in an observational treatment comparison study, measuring and adjusting for nearly all confounding in play are very important. Sometimes adjusting for confounding requires overfitting the model from a prediction standpoint, but that is OK. Overfitting can result in wider confidence intervals for the effect of interest, and that is a proper price to pay.
### Developing Models for Hypothesis Testing
1. Virtually same as previous strategy `r ipacue()`
1. Interactions require tests of effect by varying values of
another variable, or "main effect + interaction" joint tests
(e.g., is treatment effective for either sex, allowing effects to be
different)
1. Validation may help quantify over-adjustment
## Study Questions
**Section 4.1**
1. Investigators are interested in finding risk factors for stroke.
They collected data on 3000 subjects of whom 70 were known to
suffer a stroke within 5 years from study entry. They decided
that race (5 possible levels), age, height, and mean arterial blood
pressure should definitely be in the model. They do not try to
find previous studies that show how these potential risk factors
relate to the risk of stroke. What is one way to decide how many
degrees of freedom to spend on each predictor? How can one achieve
these d.f. (whatever they are) for race and for a continuous variable?
1. What is the driving force behind the approach used here to prespecify the complexity with which each predictor is specified in the regression model?
1. Why is the process fair?
1. When feasible to do, why is learning from a saturated model preferred?
**Section 4.3**
1. What did we already study that variable selection is an extension of?
1. What does variable selection ruin more than it ruins regression coefficient estimates?
1. Besides those problems what's the worst thing you can say about statistical test-based variable selection?
1. In which situation would variable selection have a chance to be helpful?
1. What is the statistical point that the Maxwell demon analogy is trying to bring out?
1. What is the single root cause of problems that is in common to each of the
following strategies?
+ The investigator retains race as 5 categories and fits it with 4
dummy variables. She examines coefficients from these dummy
variables to decide which races have similar coefficients and should
be pooled.
+ All continuous variables are allowed to be nonlinear using
splines, and variables having insignificant nonlinear terms are
re-fitted as linear.
+ All potential risk factors are used as candidate predictor
variables with forward stepwise variable selection with a
significance level for entering the model of $\alpha=0.1$.
+ A clinical trial of 5 treatments find that 3 of the treatments
result in nearly the same blood pressure reduction. These 3
treatments are pooled and their overall mean is compared with each
of the remaining 2 treatments.
1. Name at least one specific harm done by the strategies outlined in the
last question, in general terms (not specific to each strategy).
**Section 4.4**
1. Describe a major way that "breaking ties" in Y, i.e., having it more continuous, results in more power and precision in modeling.
1. What is the effective sample size in a study with 10 cancer outcomes and 100,000 normal outcomes?
**Section 4.5**
1. What are main causes of passive shrinkage/regression to the mean?
1. Why does the heuristic shrinkage estimate work?
1. What causes the graph of $\hat{Y}$ (on $x$-axis) vs.\ $Y$
(on $y$-axis; you could call this $Y_{new}$) to be flatter than a
$45^\circ$ line when the graph is made for new data not used to fit
the model?
**Section 4.6**
1. What causes the standard error of a regression coefficient to get large when adjusting for a competing predictor?
1. When just wanting to measure strength of association or test a group of predictors, what is a simple fix for co-linearity?
**Section 4.7**
1. What is the purpose of data reduction, and why does it not create
phantom degrees of freedom that need to be accounted for later in
the modeling process?
1. Name several data reduction methods for reducing the number of
regression coefficients to estimate.
1. Principal components can have unstable loadings (e.g., if you bootstrap). Why are they still a valuable component in a data reduction strategy?
1. What is the overall guidance for knowing how much unsupervised learning (data reduction) to do?
**Section 4.9**
1. Why are high leverage (far out) observations influential on regression coefficients even when Y is binary?
**Section 4.10**
1. What would make one model having much better predictive discrimination than another irrelevant?
**Section 4.12**
1. Are the steps to the default strategy complete and is the sequencing "correct"?
```{r echo=FALSE}
saveCap('04')
```