Code
y ~ age + sex + weight + waist + tricepRegression modeling meets many analytic needs:
Simplest example: confidence interval for the slope of a predictor
Confidence intervals for predicted values; simultaneous confidence intervals for a series of predicted values
Alternative: Stratification
Alternative: Single Trees (recursive partitioning/CART)
Alternative: Machine Learning
| Symbol | Meaning |
|---|---|
| \(Y\) | response (dependent) variable |
| \(X\) | \(X_{1},X_{2},\ldots,X_{p}\) – list of predictors |
| \(\beta\) | \(\beta_{0},\beta_{1},\ldots,\beta_{p}\) – regression coefficients |
| \(\beta_0\) | intercept parameter(optional) |
| \(\beta_{1},\ldots,\beta_{p}\) | weights or regression coefficients |
| \(X\beta\) | \(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p}X_{p}, X_{0}=1\) |
Model: connection between \(X\) and \(Y\)
\(C(Y|X)\) : property of distribution of \(Y\) given \(X\), e.g.
\(C(Y|X) = {\rm E}(Y|X)\) or \(\Pr(Y=1|X)\).
General regression model \[C(Y|X) = g(X) .\]
General linear regression model \[C(Y|X) = g(X\beta) .\] Examples
Linearize: \(h(C(Y|X))=X\beta,
h(u)=g^{-1}(u)\)
Example:
General linear regression model:
\(C'(Y|X)=X\beta\).
Suppose that \(X_{j}\) is linear and doesn’t interact with other \(X\)’s1.
1 Note that it is not necessary to “hold constant” all other variables to be able to interpret the effect of one predictor. It is sufficient to hold constant the weighted sum of all the variables other than \(X_{j}\). And in many cases it is not physically possible to hold other variables constant while varying one, e.g., when a model contains \(X\) and \(X^{2}\) (David Hoaglin, personal communication).
Drop \('\) from \(C'\) and assume \(C(Y|X)\) is property of \(Y\) that is linearly related to weighted sum of \(X\)’s.
Nominal (polytomous) factor with \(k\) levels : \(k-1\) indicator variables. E.g. \(T=J,K,L,M\):
\[C(Y|T) = X\beta= \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3} X_{3},\]
where
\[\begin{array}{ccc} X_{1} = 1 & {\rm if} \ \ T=K, & 0 \ \ {\rm otherwise} \nonumber\\ X_{2} = 1 & {\rm if} \ \ T=L, & 0 \ \ {\rm otherwise} \\ X_{3} = 1 & {\rm if} \ \ T=M, & 0 \ \ {\rm otherwise} \nonumber. \end{array}\]The test for any differences in the property \(C(Y)\) between treatments is \(H_{0}:\beta_{1}=\beta_{2}=\beta_{3}=0\).
\(X_{1}\) and \(X_{2}\), effect of \(X_{1}\) on \(Y\) depends on level of \(X_{2}\). One way to describe interaction is to add \(X_{3}=X_{1}X_{2}\) to model: \[C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{1}X_{2} .\]
One-unit increase in \(X_{2}\) on \(C(Y|X)\) : \(\beta_{2}+\beta_{3} X_{1}\).
Worse interactions:
If \(X_{1}\) is binary, the interaction may take the form of a difference in shape (and/or distribution) of \(X_{2}\) vs. \(C(Y)\) depending on whether \(X_{1}=0\) or \(X_{1}=1\) (e.g. logarithm vs. square root).
This paper describes how interaction effects can be misleading. See Interaction effects need interaction controls by Uri Simonsohn for an explanation of the possible need for controlling for other interactions when the interest is on a specific interaction.
Postulate the model \(C(Y|age,sex) = \beta_{0}+\beta_{1} age + \beta_{2} [sex=f] + \beta_{3} age [sex=f]\) where \([sex=f]\) is an indicator indicator variable for sex=female, i.e., the reference cell is sex=male2.
2 You can also think of the last part of the model as being \(\beta_{3} X_{3}\), where \(X_{3} = age \times [sex=f]\).
Model assumes
Interpretations of parameters:
| Parameter | Meaning |
|---|---|
| \(\beta_{0}\) | \(C(Y | age=0, sex=m)\) |
| \(\beta_{1}\) | \(C(Y | age=x+1, sex=m) - C(Y | age=x, sex=m)\) |
| \(\beta_{2}\) | \(C(Y | age=0, sex=f) - C(Y | age=0, sex=m)\) |
| \(\beta_{3}\) | \(C(Y | age=x+1, sex=f) - C(Y | age=x, sex=f) -\) |
| \([C(Y | age=x+1, sex=m) - C(Y | age=x, sex=m)]\) |
\(\beta_{3}\) is the difference in slopes (female – male).
When a high-order effect such as an interaction effect is in the model, be sure to interpret low-order effects by finding out what makes the interaction effect ignorable. In our example, the interaction effect is zero when age=0 or sex is male.
Hypotheses that are usually inappropriate:
More useful hypotheses follow. For any hypothesis need to
Most Useful Tests for Linear age \(\times\) sex Model
| Null or Alternative Hypothesis | Mathematical Statement |
|---|---|
| Effect of age is independent of sex or Effect of sex is independent of age or age and sex are additive age effects are parallel |
\(H_{0}: \beta_{3}=0\) |
| age interacts with sex age modifies effect of sex sex modifies effect of age sex and age are non-additive (synergistic) |
\(H_{a}: \beta_{3} \neq 0\) |
| age is not associated with \(Y\) | \(H_{0}: \beta_{1}=\beta_{3}=0\) |
| age is associated with \(Y\) age is associated with \(Y\) for either females or males |
\(H_{a}: \beta_{1} \neq 0 \textrm{~or~} \beta_{3} \neq 0\) |
| sex is not associated with \(Y\) | \(H_{0}: \beta_{2}=\beta_{3}=0\) |
| sex is associated with \(Y\) sex is associated with \(Y\) for some value of age |
\(H_{a}: \beta_{2} \neq 0 \textrm{~or~} \beta_{3} \neq 0\) |
| Neither age nor sex is associated with \(Y\) | \(H_{0}: \beta_{1}=\beta_{2}=\beta_{3}=0\) |
| Either age or sex is associated with \(Y\) | \(H_{a}: \beta_{1} \neq 0 \textrm{~or~} \beta_{2} \neq 0 \textrm{~or~} \beta_{3} \neq 0\) |
Note: The last test is called the global test of no association. If an interaction effect is present, there is both an age and a sex effect. There can also be age or sex effects when the lines are parallel. The global test of association (test of total association) has 3 d.f. instead of 2 (age + sex) because it allows for unequal slopes.
we may want to jointly test the association between all body measurements and response, holding age and sex constant.
anova(fit, weight, waist, tricep) if fit is a fit object created by the R rms package)Natura non facit saltus
(Nature does not make jumps)
— Gottfried Wilhelm Leibniz
 Lucy D’Agostino McGowan
Lucy D’Agostino McGowan
Relationships seldom linear except when predicting one variable from itself measured earlier
Categorizing continuous predictors into intervals is a disaster; see Royston et al. (2006), Altman (1991), Hilsenbeck & Clark (1996), Lausen & Schumacher (1996), Altman et al. (1994), Belcher (1992), Faraggi & Simon (1996), Ragland (1992), Suissa & Blais (1995), Buettner et al. (1997), Maxwell & Delaney (1993), Schulgen et al. (1994), Altman (1998), Holländer et al. (2004), Moser & Coombs (2004), Wainer (2006), Fedorov et al. (2009), Giannoni et al. (2014), Collins et al. (2016), Bennette & Vickers (2012) and Biostatistics for Biomedical Research, Chapter 18.
Some problems caused by this approach:
3 If a cutpoint is chosen that minimizes the \(P\)-value and the resulting \(P\)-value is 0.05, the true type I error can easily be above 0.5 Holländer et al. (2004).
Interactive demonstration of power loss of categorization vs. straight line and quadratic fits in OLS, with varying degree of nonlinearity and noise added to \(X\) (must run in RStudio)
Interactive demonstration of lack of fit after categorization of a continuous predictor, and comparison with spline fits, by Stefan Hansen
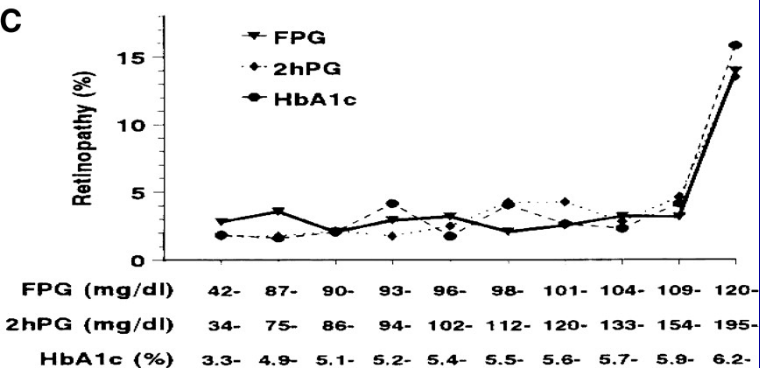
Example4 of misleading results from creating intervals (here, deciles) of a continuous predictor. Final interval is extremely heterogeneous and is greatly influenced by very large glycohemoglobin values, creating the false impression of an inflection point at 5.9.
4 From NHANES III; Diabetes Care 32:1327-34; 2009 adapted from Diabetes Care 20:1183-1197; 1997.
See this for excellent graphical examples of the harm of categorizing predictors, especially when using quantile groups.
\[C(Y|X_{1}) = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{1}^{2} .\]
More generally: \(x\)-axis divided into intervals with endpoints \(a,b,c\) (knots).
\[\begin{array}{ccc} f(X) &=& \beta_{0}+\beta_{1}X+\beta_{2}(X-a)_{+}+\beta_{3}(X-b)_{+} \nonumber\\ &+& \beta_{4}(X-c)_{+} , \end{array}\]where
\[\begin{array}{ccc} (u)_{+}=&u,&u>0 ,\nonumber\\ &0,&u\leq0 . \end{array}\]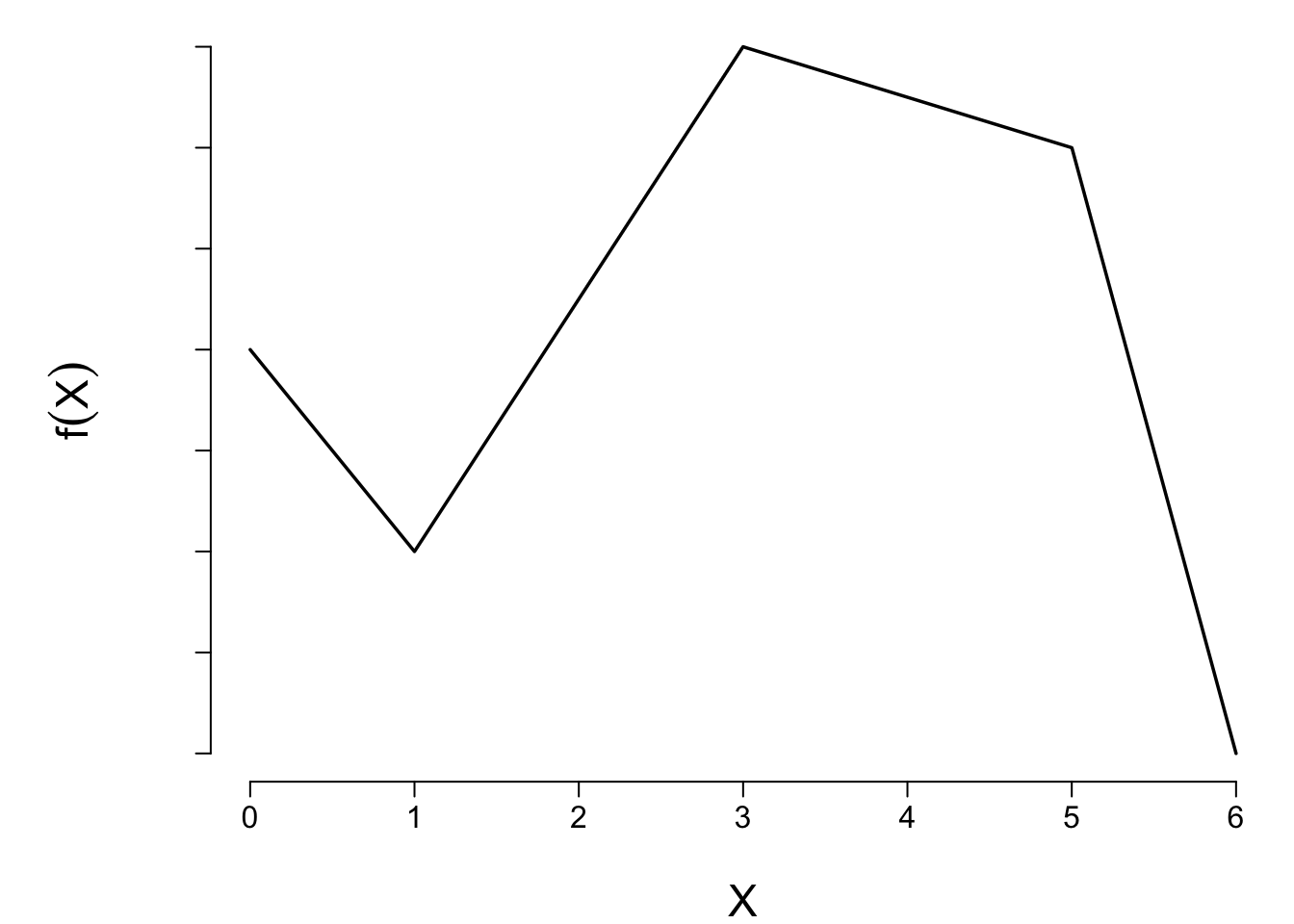
\[C(Y|X) = f(X) = X\beta,\] where \(X\beta = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3}X_{3}+\beta_{4} X_{4}\), and
\[\begin{array}{cc} X_{1}=X & X_{2} = (X-a)_{+}\nonumber\\ X_{3}=(X-b)_{+} & X_{4} = (X-c)_{+} . \end{array}\]Overall linearity in \(X\) can be tested by testing \(H_{0} : \beta_{2} = \beta_{3} = \beta_{4} = 0\).
Cubic splines are smooth at knots (function, first and second derivatives agree) — can’t see joins.
\(k\) knots \(\rightarrow k+3\) coefficients excluding intercept.
\(X^2\) and \(X^3\) terms must be included to allow nonlinearity when \(X < a\).
stats.stackexchange.com/questions/421964 has some useful descriptions of what happens at the knots, e.g.:
Knots are where different cubic polynomials are joined, and cubic splines force there to be three levels of continuity (the function, its slope, and its acceleration or second derivative (slope of the slope) do not change) at these points. At the knots the jolt (third derivative or rate of change of acceleration) is allowed to change suddenly, meaning the jolt is allowed to be discontinuous at the knots. Between knots, jolt is constant.
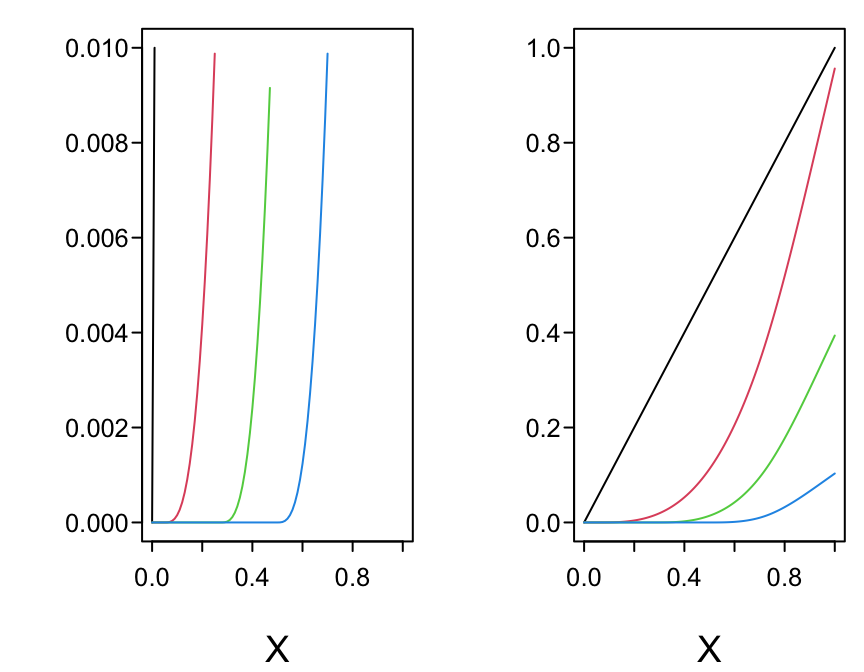
The following graphs show the function and its first three derivatives (all further derivatives are zero) for the function given by \(f(x) = x + x^{2} + 2x^{3} + 10(x - 0.25)^{3}_{+} - 50(x - 0.5)^{3}_{+} -100(x - 0.75)^{3}_{+}\) for \(x\) going from 0 to 1, where there are three knots, at \(x=0.25, 0.5, 0.75\).
spar(bty='l', mfrow=c(4,1), bot=-1.5)
x <- seq(0, 1, length=500)
x1 <- pmax(x - .25, 0)
x2 <- pmax(x - .50, 0)
x3 <- pmax(x - .75, 0)
b1 <- 1; b2 <- 1; b3 <- 2; b4 <- 10; b5 <- -50; b6 <- -100
y <- b1 * x + b2 * x^2 + b3 * x^3 + b4 * x1^3 + b5 * x2^3 + b6 * x3^3
y1 <- b1 + 2*b2*x + 3*b3*x^2 + 3*b4*x1^2 + 3*b5*x2^2 + 3*b6*x3^2
y2 <- 2*b2 + 6*b3*x + 6*b4*x1 + 6*b5*x2 + 6*b6*x3
y3 <- 6*b3 + 6*b4*(x1>0)+ 6*b5*(x2>0) + 6*b6*(x3>0)
g <- function() abline(v=(1:3)/4, col=gray(.85))
plot(x, y, type='l', ylab=''); g()
text(0, 1.5, 'Function', adj=0)
plot(x, y1, type='l', ylab=''); g()
text(0, -15, 'First Derivative: Slope\nRate of Change of Function',
adj=0)
plot(x, y2, type='l', ylab=''); g()
text(0, -125, 'Second Derivative: Acceleration\nRate of Change of Slope',
adj=0)
plot(x, y3, type='l', ylab=''); g()
text(0, -400, 'Third Derivative: Jolt\nRate of Change of Acceleration',
adj=0)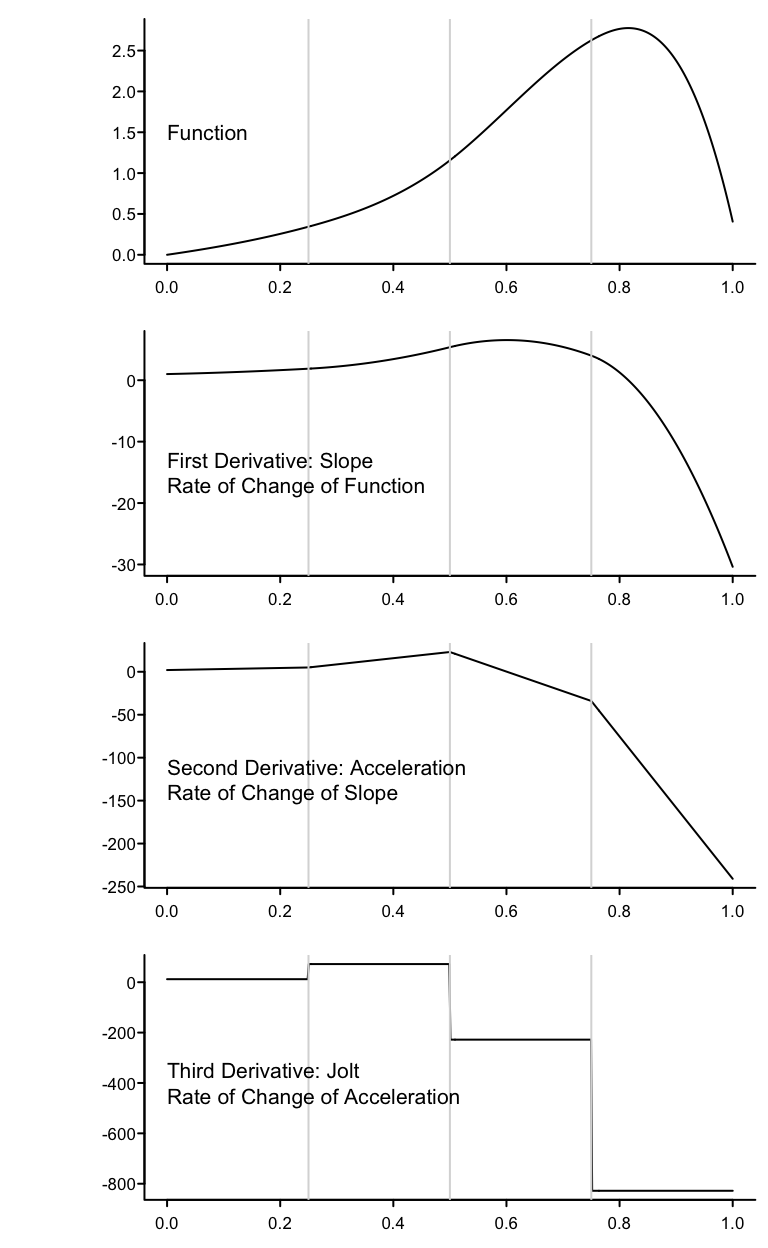
Stone & Koo (1985): cubic splines poorly behaved in tails. Constrain function to be linear in tails.
\(k+3 \rightarrow k-1\) parameters Devlin & Weeks (1986).
To force linearity when \(X < a\): \(X^2\) and \(X^3\) terms must be omitted
To force linearity when \(X\) is beyond the last knot: last two \(\beta\) s are redundant, i.e., are just combinations of the other \(\beta\) s.
The restricted spline function with \(k\) knots \(t_{1}, \ldots, t_{k}\) is given by Devlin & Weeks (1986) \[f(X) = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\ldots+\beta_{k-1} X_{k-1},\] where \(X_{1} = X\) and for \(j=1, \ldots, k-2\),
\[\begin{array}{ccc} X_{j+1} &= &(X-t_{j})_{+}^{3}-(X-t_{k-1})_{+}^{3} (t_{k}-t_{j})/(t_{k}-t_{k-1})\nonumber\\ &+&(X-t_{k})_{+}^{3} (t_{k-1}-t_{j})/(t_{k}-t_{k-1}). \end{array} \tag{2.1}\]
\(X_{j}\) is linear in \(X\) for \(X\geq t_{k}\).
For numerical behavior and to put all basis functions for \(X\) on the same scale, R Hmisc and rms package functions by default divide the terms above by \(\tau = (t_{k} - t_{1})^{2}\).
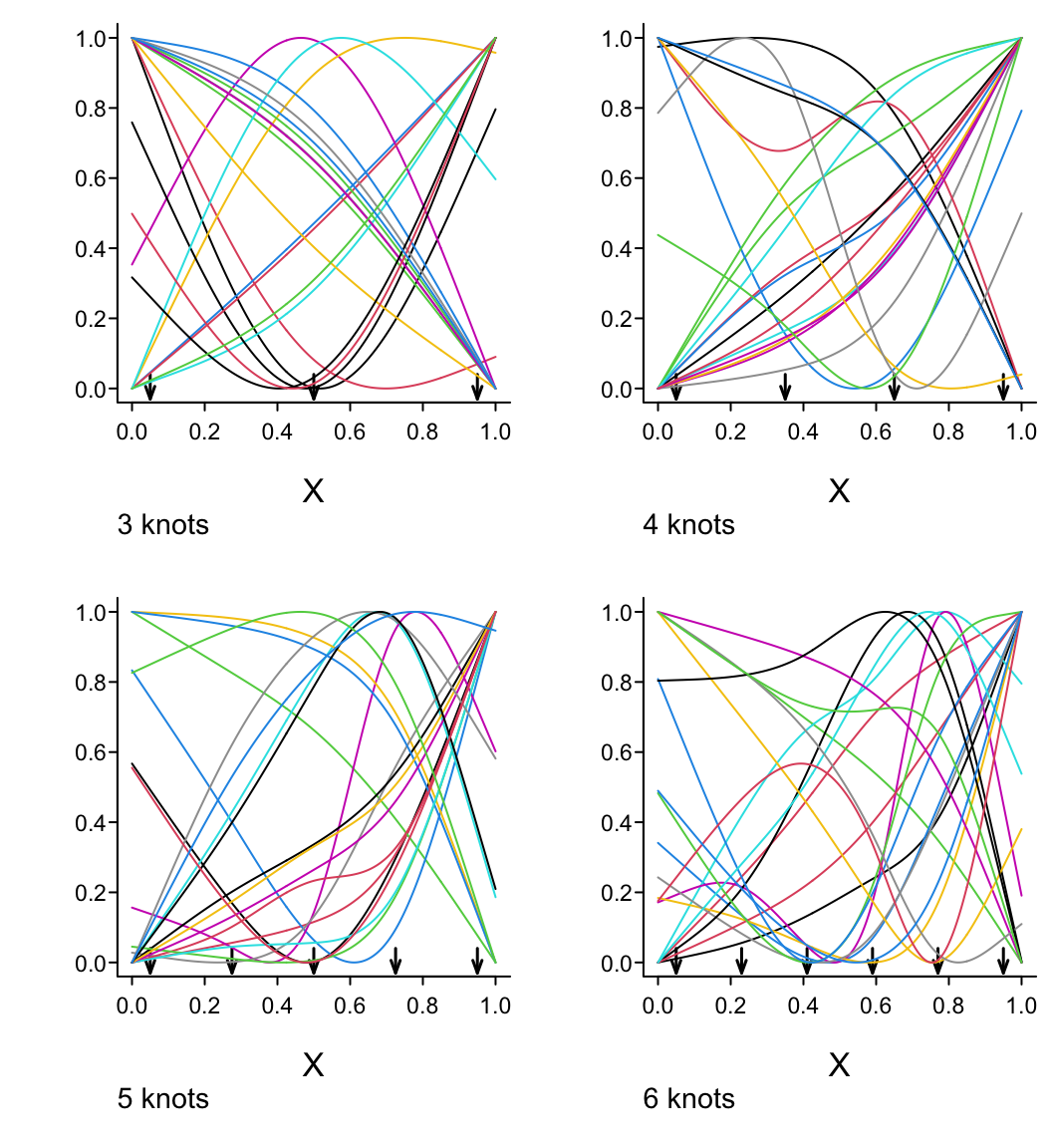
spar(left=-2, bot=2, mfrow=c(2,2), ps=13)
x <- seq(0, 1, length=300)
for(nk in 3:6) {
set.seed(nk)
knots <- seq(.05, .95, length=nk)
xx <- rcspline.eval(x, knots=knots, inclx=T)
for(i in 1 : (nk - 1))
xx[,i] <- (xx[,i] - min(xx[,i])) /
(max(xx[,i]) - min(xx[,i]))
for(i in 1 : 20) {
beta <- 2*runif(nk-1) - 1
xbeta <- xx %*% beta + 2 * runif(1) - 1
xbeta <- (xbeta - min(xbeta)) /
(max(xbeta) - min(xbeta))
if(i == 1) {
plot(x, xbeta, type="l", lty=1,
xlab=expression(X), ylab='', bty="l")
title(sub=paste(nk,"knots"), adj=0, cex=.75)
for(j in 1 : nk)
arrows(knots[j], .04, knots[j], -.03,
angle=20, length=.07, lwd=1.5)
}
else lines(x, xbeta, col=i)
}
}
Interactive demonstration of linear and cubic spline fitting, plus ordinary \(4^{th}\) order polynomial. This can be run with RStudio or in an ordinary R session.
Paul Lambert’s excellent self-contained interactive demonstrations of continuity restrictions, cubic polynomial, linear spline, cubic spline, and restricted cubic spline fitting is at pclambert.net/interactive_graphs. Jordan Gauthier has another nice interactive demonstration at drjgauthier.shinyapps.io/spliny.
Once \(\beta_{0}, \ldots, \beta_{k-1}\) are estimated, the restricted cubic spline can be restated in the form
\[\begin{array}{ccc} f(X) &=& \beta_{0}+\beta_{1}X+\beta_{2}(X-t_{1})_{+}^{3}+\beta_{3}(X-t_{2})_{+}^{3}\nonumber\\ && +\ldots+ \beta_{k+1}(X-t_{k})_{+}^{3} \end{array} \tag{2.2}\]
by dividing \(\beta_{2},\ldots,\beta_{k-1}\) by \(\tau\) and computing
\[\begin{array}{ccc} \beta_{k} &=& [\beta_{2}(t_{1}-t_{k})+\beta_{3}(t_{2}-t_{k})+\ldots\nonumber\\ && +\beta_{k-1}(t_{k-2}-t_{k})]/(t_{k}-t_{k-1})\nonumber\\ \beta_{k+1} &= & [\beta_{2}(t_{1}-t_{k-1})+\beta_{3}(t_{2}-t_{k-1})+\ldots\\ && + \beta_{k-1}(t_{k-2}-t_{k-1})]/(t_{k-1}-t_{k})\nonumber . \end{array}\]A test of linearity in X can be obtained by testing
\[H_{0} : \beta_{2} = \beta_{3} = \ldots = \beta_{k-1} = 0.\]
Example: Selvin et al. (2010)
k
|
Quantiles
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 3 | .10 | .5 | .90 | |||||
| 4 | .05 | .35 | .65 | .95 | ||||
| 5 | .05 | .275 | .5 | .725 | .95 | |||
| 6 | .05 | .23 | .41 | .59 | .77 | .95 | ||
| 7 | .025 | .1833 | .3417 | .5 | .6583 | .8167 | .975 | |
\(n<100\) – replace outer quantiles with 5th smallest and 5th largest \(X\) (Stone & Koo (1985)).
Choice of \(k\):
See Govindarajulu et al. (2007) for a comparison of restricted cubic splines, fractional polynomials, and penalized splines.
| \(X\): | 1 | 2 | 3 | 5 | 8 |
|---|---|---|---|---|---|
| \(Y\): | 2.1 | 3.8 | 5.7 | 11.1 | 17.2 |
5 Weight here means something different than regression coefficient. It means how much a point is emphasized in developing the regression coefficients.
6 These place knots at all the observed data points but penalize coefficient estimates towards smoothness.
Regression splines have several advantages (Harrell et al. (1988)):
Breiman et al. (1984): CART (Classification and Regression Trees) — essentially model-free
Method:
Advantages/disadvantages of recursive partitioning:
See Austin et al. (2010).
The approaches recommended in this course are
The data reduction approach can yield very interpretable, stable models, but there are many decisions to be made when using a two-stage (reduction/model fitting) approach, Newer approaches are evolving, including the following. These new approach handle continuous predictors well, unlike recursive partitioning.
One problem prevents most of these methods from being ready for everyday use: they require scaling predictors before fitting the model. When a predictor is represented by nonlinear basis functions, the scaling recommendations in the literature are not sensible. There are also computational issues and difficulties obtaining hypothesis tests and confidence intervals.
When data reduction is not required, generalized additive models Hastie & Tibshirani (1990), Wood (2006) should also be considered.
Considerations in Choosing One Approach over Another
A statistical model may be the better choice if
Machine learning may be the better choice if
But see this for navigating resources exposing problems in ML applications such as the following:
\[C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{2}^{2} ,\] \(H_{0}: \beta_{2}=\beta_{3}=0\) with 2 d.f. to assess association between \(X_{2}\) and outcome.
In the 5-knot restricted cubic spline model \[C(Y|X) = \beta_{0}+\beta_{1}X+\beta_{2}X'+\beta_{3}X''+\beta_{4}X''' ,\] \(H_{0}: \beta_{1}=\ldots=\beta_{4}=0\)
Grambsch & O’Brien (1991) elegantly described the hazards of pretesting
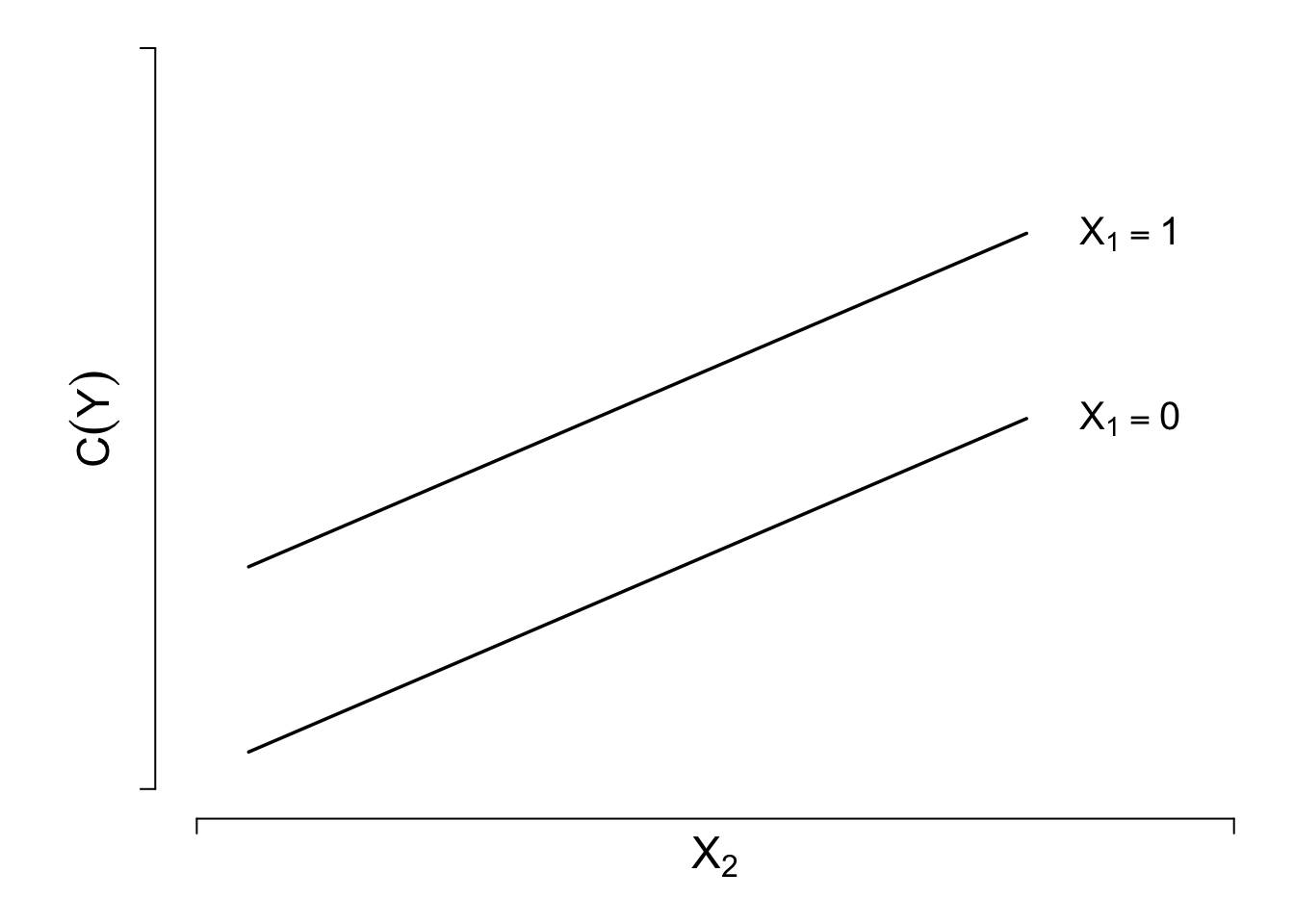
The general linear regression model is \[C(Y|X) = X\beta =\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{k}X_{k} .\] Verify linearity and additivity. Special case: \[C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2},\] where \(X_{1}\) is binary and \(X_{2}\) is continuous.
Methods for checking fit:
1. Fit simple linear additive model and check examine residual plots for patterns
qqnorm plots of overall and stratified residualsAdvantage: Simplicity
Disadvantages:
2. Scatterplot of \(Y\) vs. \(X_{2}\) using different symbols according to values of \(X_{1}\)
Advantages: Simplicity, can see interaction
Disadvantages:
3. Stratify the sample by \(X_{1}\) and quantile groups (e.g. deciles) of \(X_{2}\); estimate \(C(Y|X_{1},X_{2})\) for each stratum
Advantages: Simplicity, can see interactions, handles censored \(Y\) (if you are careful)
Disadvantages:
4. Separately for levels of \(X_{1}\) fit a nonparametric smoother relating \(X_{2}\) to \(Y\)
Advantages: All regression aspects of the model can be summarized efficiently with minimal assumptions
Disadvantages:
5. Fit flexible nonlinear parametric model
Advantages:
Disadvantages:
Confidence limits, formal inference can be problematic for methods 1-4.
Restricted cubic spline works well for method 5.
\[\begin{array}{ccc} \hat{C}(Y|X) &=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+\hat{\beta}_{2}X_{2}+\hat{\beta}_{3}X_{2}'+\hat{\beta}_{4}X_{2}'' \nonumber\\ &=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+\hat{f}(X_{2}) , \end{array}\]where \[\hat{f}(X_{2}) = \hat{\beta}_{2}X_{2}+\hat{\beta}_{3}X_{2}'+\hat{\beta}_{4}X_{2}'' ,\] \(\hat{f}(X_{2})\) spline-estimated transformation of \(X_{2}\).
Overall test of linearity \(H_{0}: \beta_{3}=\beta_{4}=\beta_{6}=\beta_{7}=0\), with 4 d.f.
Note: Interactions will be misleading if main effects are not properly modeled (M. Zhang et al. (2020)).
Suppose \(X_1\) binary or linear, \(X_2\) continuous:
Simultaneous test of linearity and additivity: \(H_{0}: \beta_{3} = \ldots = \beta_{7} = 0\).
\[\begin{array}{ccc} C(Y|X) & = & \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{1}'+\beta_{3}X_{1}'' \nonumber\\ &+& \beta_{4}X_{2}+\beta_{5}X_{2}'+\beta_{6}X_{2}'' \nonumber\\ &+& \beta_{7}X_{1}X_{2}+\beta_{8}X_{1}X_{2}'+\beta_{9}X_{1}X_{2}'' \\ &+& \beta_{10}X_{2}X_{1}'+\beta_{11}X_{2}X_{1}'' \nonumber \end{array} \tag{2.3}\]
General spline surface:
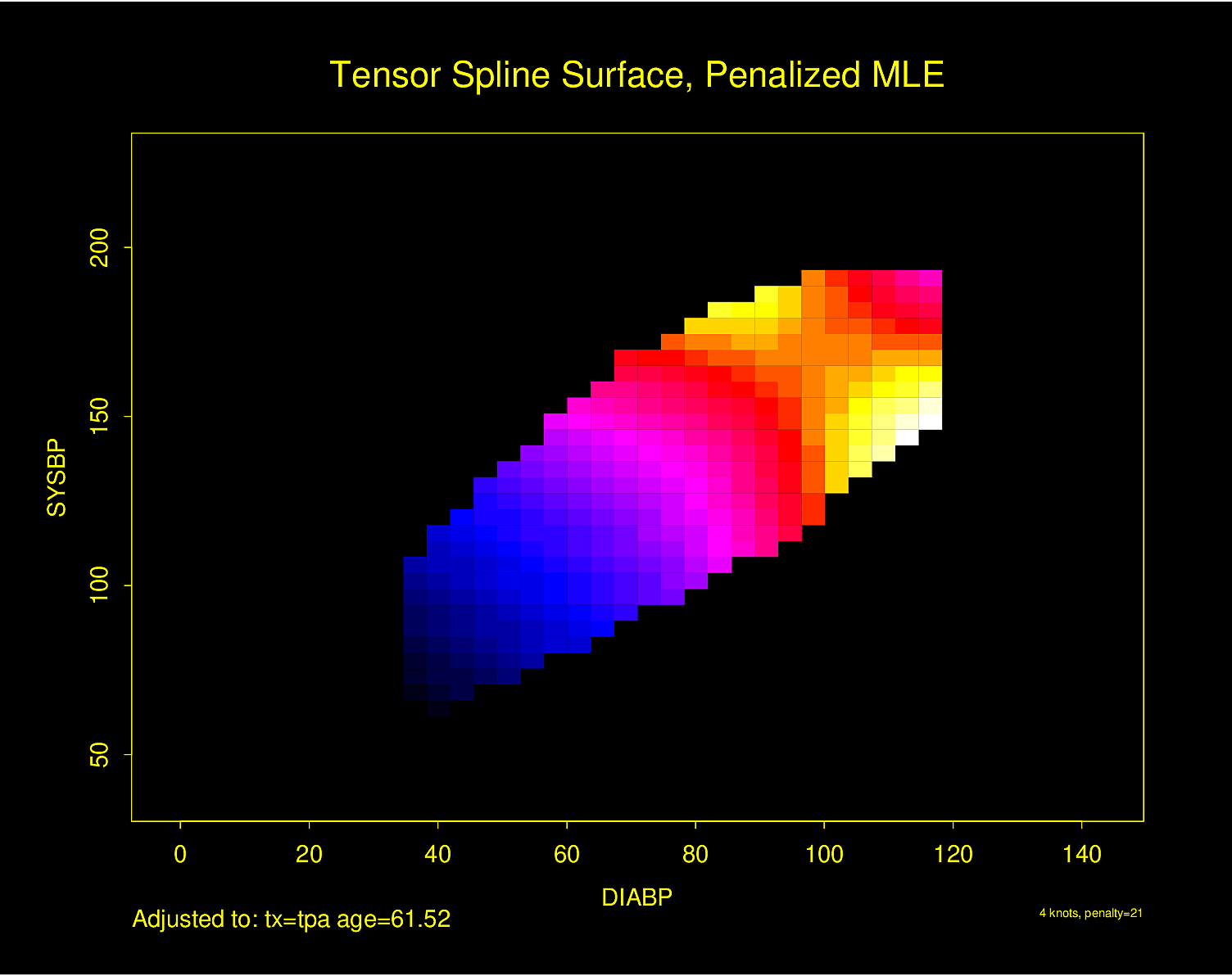
Figure 2.6 is particularly interesting because the literature had suggested (based on approximately 24 strokes) that pulse pressure was the main cause of hemorrhagic stroke whereas this flexible modeling approach (based on approximately 230 strokes) suggests that mean arterial blood pressure (roughly a \(45^\circ\) line) is what is most important over a broad range of blood pressures. At the far right one can see that pulse pressure (axis perpendicular to \(45^\circ\) line) may have an impact although a non-monotonic one.
Other issues:
Some types of interactions to pre-specify in clinical studies:
The last example is worth expanding as an example in model formulation. Consider the following study.
B7age and sexR rms package to fit a Cox proportional hazards modelsampleAge tests the adequacy of assuming a plain logarithmic trend in sample age7 For continuous \(Y\) one might need to model the residual variance of \(Y\) as increasing with sample age, in addition to modeling the mean function.
The B \(\times\) sampleAge interaction effects have 6 d.f. and tests whether the sample deterioration affects the effect of B. By not assuming that B has the same effect for old samples as for young samples, the investigator will be able to estimate the effect of B on outcome when the blood analysis is ideal by inserting sampleAge = 1 day when requesting predicted values as a function of B.
R ordSmooth package) or Bayesian shrinkage (R brms package).rms package gTrans function documented at hbiostat.org/R/rms/gtrans.htmlgTrans but harder to plot predicted values, get contrasts, and get chunk testsStart with a standard restricted cubic spline fit, 6 knots at default quantile locations. From the fitted Poisson model we estimate the number of cases per a constant population size of 100,000.
require(ggplot2)
g <- function(x) exp(x) * 100000
off <- list(stdpop=mean(d$stdpop)) # offset for prediction (383464.4)
w <- geom_point(aes(x=time, y=rate), data=d)
v <- geom_vline(aes(xintercept=37, col=I('red')))
yl <- ylab('Acute Coronary Cases Per 100,000')
f <- Glm(aces ~ offset(log(stdpop)) + rcs(time, 6),
data=d, family='poisson')
f$aic[1] 721.5237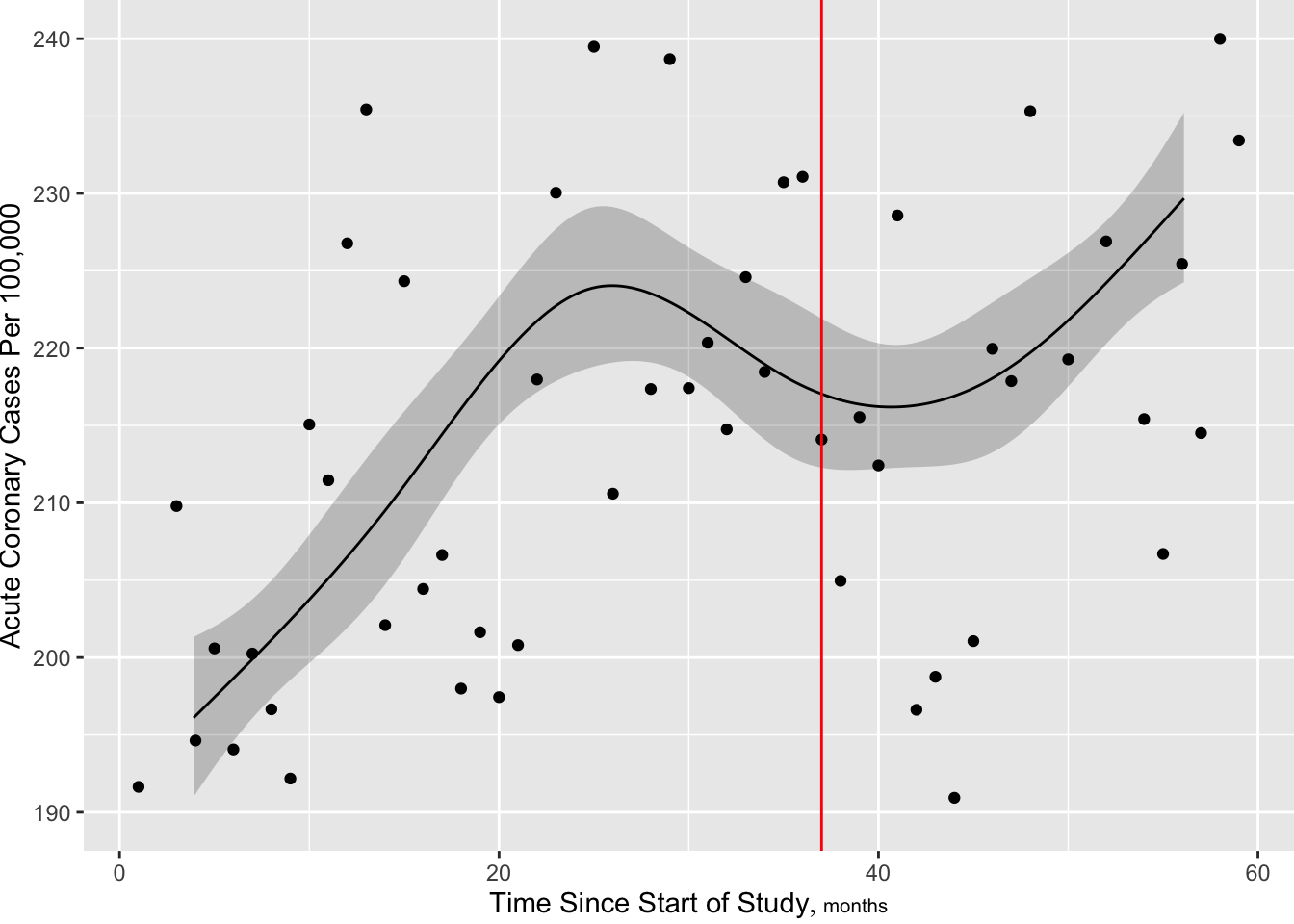
[1] 5.00 14.34 24.78 35.22 45.66 55.00[1] 674.112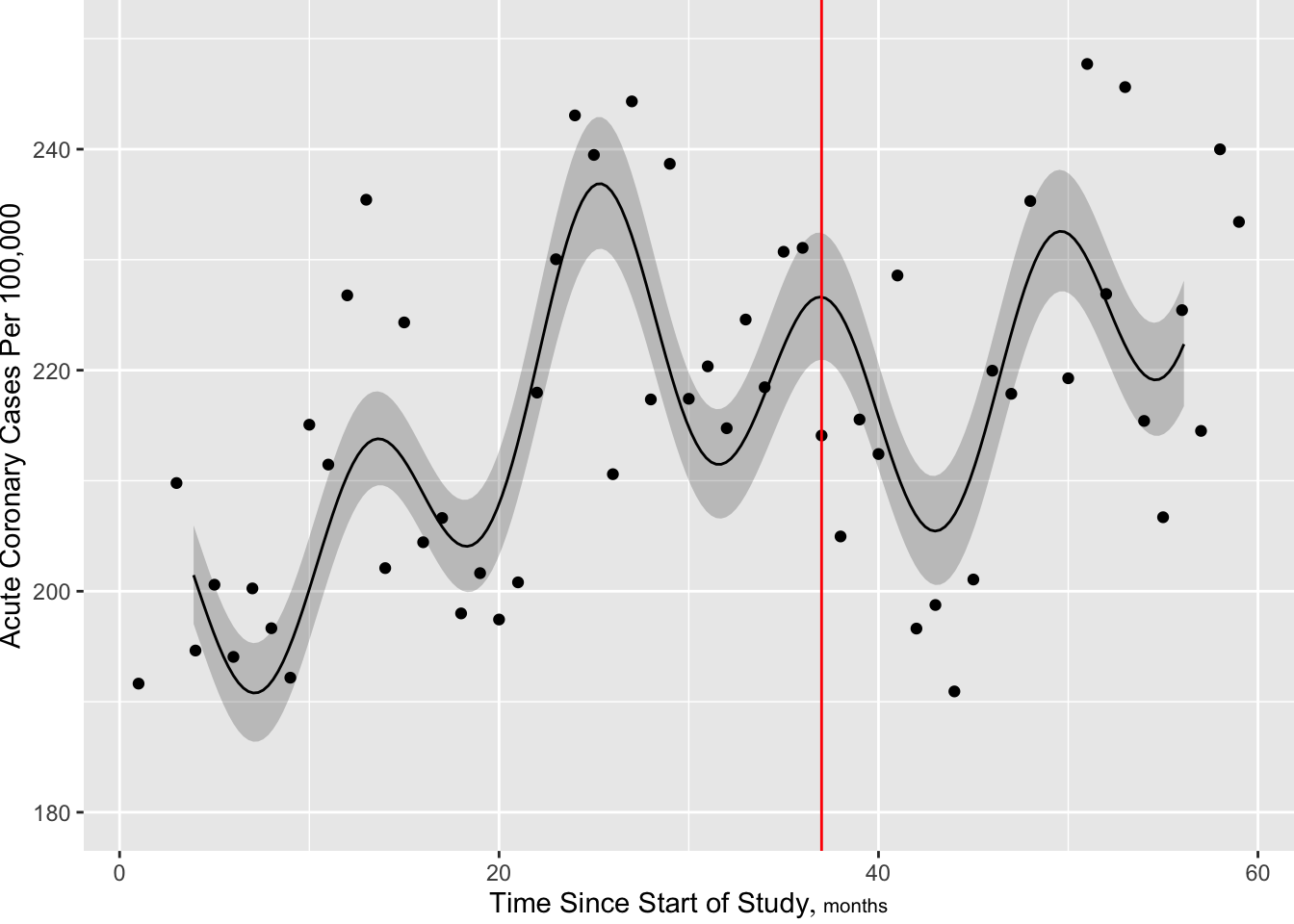
Next add more knots near intervention to allow for sudden change
[1] 661.7904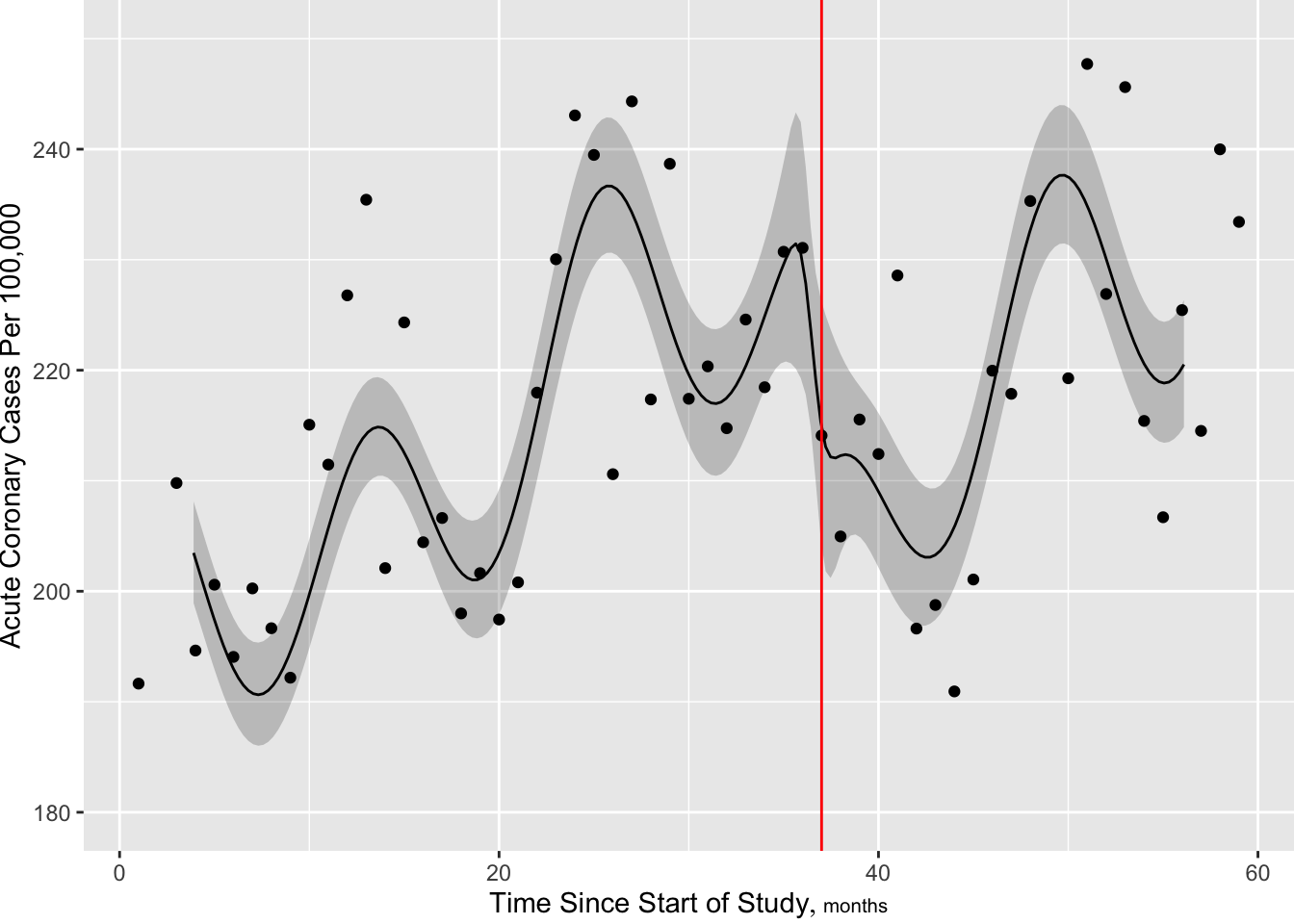
Now make the slow trend simpler (6 knots) but add a discontinuity at the intervention. More finely control times at which predictions are requested, to handle discontinuity.
[1] 659.6044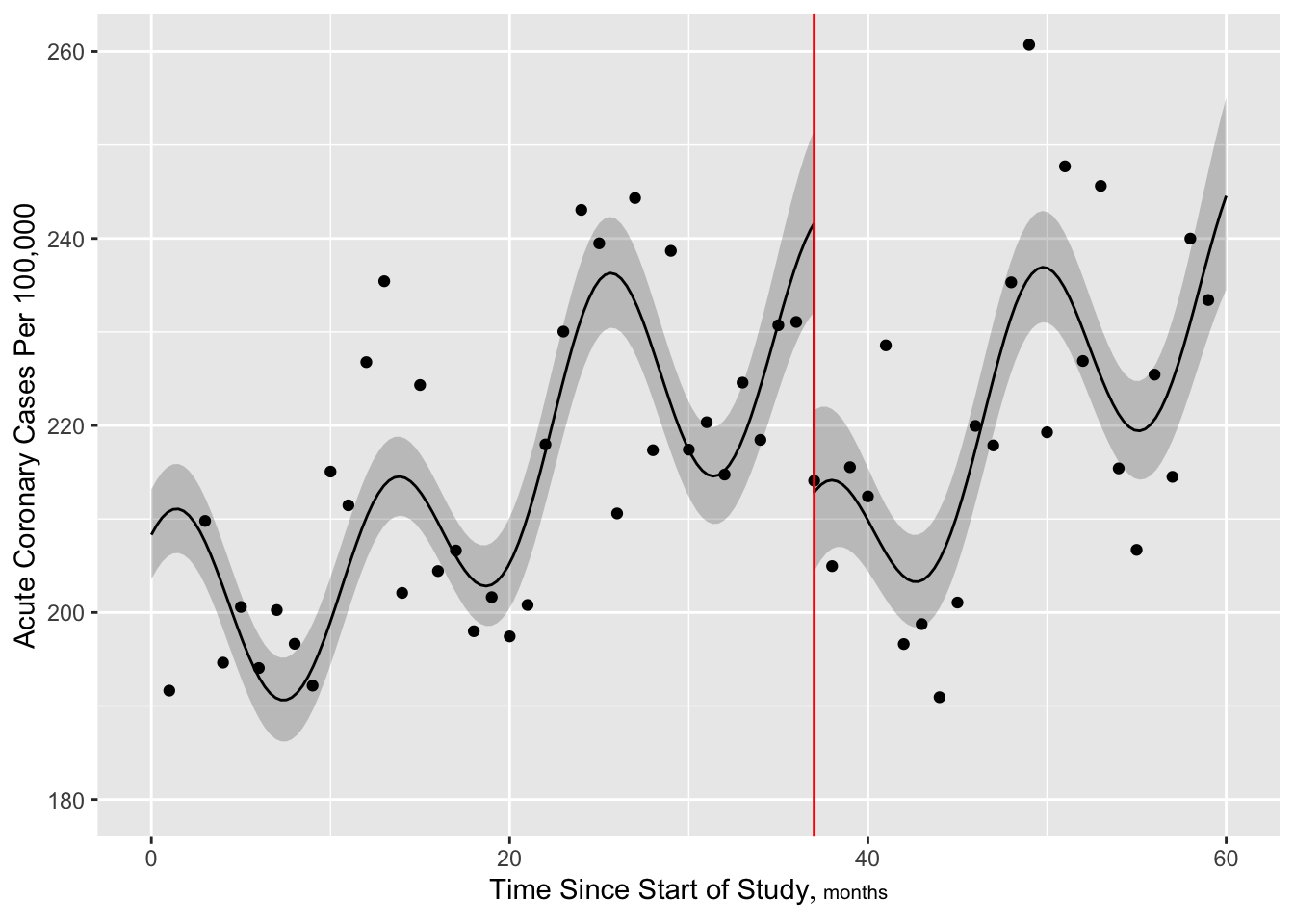
Look at fit statistics especially evidence for the jump
General Linear Model
Glm(formula = aces ~ offset(log(stdpop)) + gTrans(time, h), family = "poisson",
data = d, x = TRUE, y = TRUE)
| Model Likelihood Ratio Test |
|
|---|---|
| Obs 59 | LR χ2 169.64 |
| Residual d.f. 51 | d.f. 7 |
| g 0.080 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| Intercept | -6.2118 | 0.0095 | -656.01 | <0.0001 |
| time | 0.0635 | 0.0113 | 5.63 | <0.0001 |
| time' | -0.1912 | 0.0433 | -4.41 | <0.0001 |
| time'' | 0.2653 | 0.0760 | 3.49 | 0.0005 |
| time''' | -0.2409 | 0.0925 | -2.61 | 0.0092 |
| sin | 0.0343 | 0.0067 | 5.11 | <0.0001 |
| cos | 0.0380 | 0.0065 | 5.86 | <0.0001 |
| jump | -0.1268 | 0.0313 | -4.06 | <0.0001 |
Compute likelihood ratio \(\chi^2\) test statistics for this model
Likelihood Ratio Statistics for aces |
|||
| χ2 | d.f. | P | |
|---|---|---|---|
| time | 169.64 | 7 | <0.0001 |
| Nonlinear | 127.03 | 6 | <0.0001 |
| TOTAL | 169.64 | 7 | <0.0001 |
Get a joint LR test of seasonality and discontinuity by omitting 3 terms from the model
Contrasts allow one to estimate and test any kind of effects that are napped to the model’s regression parameters. Examples in Section 2.10.2 show how far you can take this idea, including double difference contrasts for estimating interaction effects or degree of nonlinearity. The rms package contrast.rms function makes it easy to estimate contrasts to get estimates such as the effect of age changing from 30 to 50 for males. Contrasts are just differences in predicted values, so all that’s needed is to specify the design matrices for one condition vs. another and to subtract these two matrices and multiply this difference by \(\hat{\beta}\). A standard formula is used to compute standard errors of such contrasts which leads to Wald confidence intervals.
Since Wald confidence intervals for contrasts are so easy to compute, it is tempting to always compute contrasts in an after-fitting step. This is optimal for bootstrapping, or for Bayesian models where the contrast is computed separately for each posterior draw, leading to posterior samples of the contrasts, which are summarized exactly as basic parameters are summarized (posterior median, highest posterior density uncertainty interval, etc.). But in a frequentist setting outside of a standard Gaussian linear model, Wald confidence intervals are not ideal. For example the sampling distribution of the contrast may be asymmetric, so symmetric confidence intervals may have poor coverage on at least one side. In addition, Wald confidence intervals may inconsistent with gold-standard likelihood ratio \(\chi^2\) tests, whereas profile likelihood confidence intervals are consistent with them.
To compute profile likelihood confidence intervals on a contrast, one must reparameterize the model with \(p\) parameters so that the contrast is represented by a single variable, with the model’s \(p-1\) parameters reparameterized so that the contrast and the \(p-1\) parameters span the same space as the original model. This allows profile likelihood algorithms to fix the contrast “parameter” at a given constant \(c\), compute maximum likelihood estimates of the remaining new parameters, and repeat this process many times to solve for the two values of \(c\) such that the interval between them is the set of values that if hyothesized to be true would not lead to rejection of the null using the likelihood ratio \(\chi^2\) test.
How does one derive the “contrast variable” and the remaining \(p-1\) variables? How can the contrast variable be constructed so that its estimated regression coefficient is exactly equal to the estimated contrast? This is a useful exercise in understanding regression model algebra even if not using profile likelihoods.
Consider a very simple case where the model is \(E(Y | X=x) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} = f(x_1, x_2)\), where the vector \(x\) is \([x_1, x_2]\). Suppose the contrast of interest is just \(\beta_1\), i.e., the contrast is \(f(1, a) - f(0, a)\). The setting for \(x_2\), \(a\), is irrelevant and will cancel out since \(x_1\) and \(x_2\) do not interact. Se we are not reparameterizing the model; the matrix multiplication that translates from the original \(x\) space to the new space involves a \(2\times 2\) identity matrix, and one fits the model with the original \(x\) values to get the contrast of interest as the \(\hat{\beta_1}\).
Next consider a more meaningful case there the contrast of interest is \(\beta_1 - \beta_2\). Intuition tells us that the rephrasing of parameters needed for the model’s second variable is \(\beta_1 + \beta_2\) which is orthogonal to the first combination. Let’s use a general procedure to derive this second parameter. If we augment the first new parameter with the identity matrix that represents the original model, a singular value decomposition will yield the second variable that will make the modified model span the same space as the original. The R code below demonstrates this.
[,1] [,2]
D 1 -1
1 0
0 1$d
[1] 1.732051 1.000000
$u
[,1] [,2]
[1,] -0.8164966 1.855775e-16
[2,] -0.4082483 -7.071068e-01
[3,] 0.4082483 -7.071068e-01
$v
[,1] [,2]
[1,] -0.7071068 -0.7071068
[2,] 0.7071068 -0.7071068 [,1]
[1,] -0.7071068
[2,] -0.7071068The coefficients of \(x_1\) and \(x_2\) in v are the same, so the second parameter is associated with the sum of \(x_1\) and \(x_2\), with an arbitrary scaling constant.
Now consider a more interested case. A model has a predictor \(x\) that is modeled with an ordinary cubic polynomial plus a discontinuity at \(x=3\) and includes another covariate \(z\):
\[ \begin{aligned} E(Y | x, z) = f(x, z) &= \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 \\ &+ \beta_4 [x > 3] + \beta_5 z \end{aligned} \]
Here \([s]\) is a 0/1 indicator variable for the truth of assertion \(s\). Our contrast of interest is \(f(3, a) - f(1, a)\) which is \(2\beta_1 + 8\beta_2 + 26\beta_3\). \(a\) cancels out and \(\beta_4\) is not involved either since \(x \leq 3\) for both contrast predictor settings. We need to create a new variable \(u\) that, when adjusted for the correct parameterization of the other variables, will result in a regression coefficient that is exactly \(2\beta_1 + 8\beta_2 + 26\beta_3\) in the original \(\beta\)s. Try \(u = (\frac{x}{2} + \frac{x^2}{8} + \frac{x^3}{26}) / 3\). Simulate some data and use the singular value decomposition to solve for the matrix to multiply the design matrix by to reparameterize the other parts of the model. Below xc (x contrast variable) is \(u\).
set.seed(1)
n <- 100; b0=3; b1=1; b2=.2; b3=.05; b4=1; b5=2
x <- 2 * rnorm(n)
z <- rnorm(n)
res <- 2 * rnorm(n)
d <- data.frame(x, z)
dd <- datadist(d); options(datadist='dd')
y <- b0 + b1*x + b2*x^2 + b3*x^3 + b4*(x > 3) + b5*z + res
# Form a general transformation function fo x
g <- function(x) cbind(x=x, x2=x^2, x3=x^3, x4=x > 3)
f <- orm(y ~ gTrans(x, g) + z, x=TRUE, y=TRUE)
fLogistic (Proportional Odds) Ordinal Regression Model
orm(formula = y ~ gTrans(x, g) + z, x = TRUE, y = TRUE)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 100 | LR χ2 149.06 | R2 0.775 | ρ 0.833 |
| ESS 100 | d.f. 5 | R25,100 0.763 | Dxy 0.651 |
| Distinct Y 100 | Pr(>χ2) <0.0001 | R25,100 0.763 | |
| Y0.5 3.747608 | Score χ2 245.33 | |Pr(Y ≥ median)-½| 0.333 | |
| max |∂log L/∂β| 9×10-13 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| x | 0.4238 | 0.2150 | 1.97 | 0.0487 |
| x2 | 0.2207 | 0.0800 | 2.76 | 0.0058 |
| x3 | 0.1179 | 0.0304 | 3.88 | 0.0001 |
| x4 | 1.6193 | 1.7626 | 0.92 | 0.3583 |
| z | 1.7016 | 0.2337 | 7.28 | <0.0001 |
gTrans(x, g)x gTrans(x, g)x2 gTrans(x, g)x3 gTrans(x, g)x4 z
1 1 1 1 0 3.141593
1 3 9 27 0 3.141593 gTrans(x, g)x gTrans(x, g)x2 gTrans(x, g)x3 gTrans(x, g)x4 z
1 2 8 26 0 0 [,1]
1 5.678912 gTrans(x, g)x gTrans(x, g)x2 gTrans(x, g)x3 gTrans(x, g)x4 z
1 2 8 26 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1$d
[1] 27.29469 1.00000 1.00000 1.00000 1.00000
$u
[,1] [,2] [,3] [,4] [,5]
[1,] 0.999328634 -3.097952e-18 0 0 -1.260631e-16
[2,] 0.002686367 6.195905e-18 0 0 9.973082e-01
[3,] 0.010745469 -9.557790e-01 0 0 -2.156342e-02
[4,] 0.034922775 2.940858e-01 0 0 -7.008112e-02
[5,] 0.000000000 0.000000e+00 -1 0 0.000000e+00
[6,] 0.000000000 0.000000e+00 0 -1 0.000000e+00
$v
[,1] [,2] [,3] [,4] [,5]
[1,] 0.07332356 0.0000000 0 0 0.99730821
[2,] 0.29329423 -0.9557790 0 0 -0.02156342
[3,] 0.95320625 0.2940858 0 0 -0.07008112
[4,] 0.00000000 0.0000000 -1 0 0.00000000
[5,] 0.00000000 0.0000000 0 -1 0.00000000 [,1] [,2] [,3] [,4] [,5]
[1,] 2 0.000000 0.00000 0.00000 27.2029410
[2,] 8 -26.070176 0.00000 0.00000 -0.5881717
[3,] 26 8.021592 0.00000 0.00000 -1.9115580
[4,] 0 0.000000 -27.27636 0.00000 0.0000000
[5,] 0 0.000000 0.00000 -27.27636 0.0000000 [,1] [,2] [,3] [,4] [,5]
[1,] 0.002688172 0.00000000 0.00000000 0.00000000 0.0365630928
[2,] 0.010752688 -0.03504056 0.00000000 0.00000000 -0.0007905534
[3,] 0.034946237 0.01078171 0.00000000 0.00000000 -0.0025692984
[4,] 0.000000000 0.00000000 -0.03666178 0.00000000 0.0000000000
[5,] 0.000000000 0.00000000 0.00000000 -0.03666178 0.0000000000Logistic (Proportional Odds) Ordinal Regression Model
orm(formula = y ~ Z)
| Model Likelihood Ratio Test |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 100 | LR χ2 149.06 | R2 0.775 | ρ 0.833 |
| ESS 100 | d.f. 5 | R25,100 0.763 | Dxy 0.651 |
| Distinct Y 100 | Pr(>χ2) <0.0001 | R25,100 0.763 | |
| Y0.5 3.747608 | Score χ2 245.33 | |Pr(Y ≥ median)-½| 0.333 | |
| max |∂log L/∂β| 4×10-13 | Pr(>χ2) <0.0001 |
| β | S.E. | Wald Z | Pr(>|Z|) | |
|---|---|---|---|---|
| Z[1] | 5.6789 | 1.0985 | 5.17 | <0.0001 |
| Z[2] | -4.8087 | 1.9667 | -2.45 | 0.0145 |
| Z[3] | -44.1680 | 48.0777 | -0.92 | 0.3583 |
| Z[4] | -46.4143 | 6.3740 | -7.28 | <0.0001 |
| Z[5] | 11.1745 | 5.8960 | 1.90 | 0.0581 |
Compute the contrast on the original variables and compare to the coefficient of xc.
z Contrast S.E. Lower Upper Z Pr(>|z|)
1 -0.1772172 5.678912 1.098531 3.525831 7.831994 5.17 0
Confidence intervals are 0.95 individual intervals[1] 5.678912Repeat using the more accurate profile likelihood method, which makes use of the singular value decomposition like the one above.
z Contrast Lower Upper Χ² Pr(>Χ²)
1 -0.1772172 5.678912 3.626648 7.9426 36.37 0
Confidence intervals are 0.95 profile likelihood intervalsNote that singular value decompositions have arbitrary signs. The contrast function does any needed sign reversal so that the contrast matches the original one.
There are many advantages to fitting models with a Bayesian approach when compared to the frequentist / maximum likelihood approach that receives more coverage in this text. These advantages include
As seen in example output form the blrm function below, one can automatically obtain highest posterior density uncertainty intervals for any parameter including overall model performance metrics. These are derived from the \(m\) posterior draws of the model’s parameters by computing the model performance metric for each draw. The uncertainties captured by this process relate to the ability to well-estimate model parameters, which relates also to within-training-sample model fit. So the uncertainties reflect a similar phenomenon to what \(R^{2}_\text{adj}\) measures. Adjusted \(R^2\) other than McFadden’s penalize for \(p\), the number of regression parameters estimated, other than the intercept. This is very similar to considering likelihood ratio \(\chi^2\) statistics minus the number of degrees of freedom involved in the LR test. On the other hand, AIC approximates out-of-sample model performance by using a penalty of twice the degrees of freedom (like the seldom-used McFadden \(R^{2}_\text{adj}\))
So uncertainties computed by the blrm function come solely from the spread of the posterior distributions, i.e., the inability of the analysis to precisely estimate the unknown parameters. They condition on the observed design matrix \(X\) and do not consider other samples as would be done with out-of-sample predictive accuracy assessment with AIC, the bootstrap, or cross-validation.
When \(p=1\) a rank measure of predictive discrimination such as \(D_{xy}\) will have no uncertainty unless the sign of the one regression coefficient often flips over posterior draws.
A major part of the arsenal of Bayesian modeling weapons is Stan based at Columbia University. Very general R statistical modeling packages such as brms and rstanarm are based on Stan.
RMS has several fully worked-out Bayesian modeling case studies. The purpose of the remainder of this chapter is to show the power of Bayes in general regression modeling.
With a Bayesian approach one can include a parameter for each aspect of the model you know exists but are unsure about. This leads to results that are not overly optimistic, because uncertainty intervals will be a little wider to acknowledge what you don’t know. A good example is the Bayesian \(t\)-test, which has a parameter for the amount of non-normality and a parameter for how unequal the variances may be in the two groups being compared. Prior distributions can favor normality and equal variance, and modeling becomes more flexible as \(n \uparrow\).
Other examples of borrowing information and adding flexibility:
Interactions bring special problems to estimation and inference. In the best of cases, an interaction requires \(4 \times\) larger sample size to estimate and may require \(16 \times\) the sample size to achieve the same power as a main effect test. We need a way to borrow information, essentially having an interaction term “half in” and “half out” of the model. This has been elegantly described by R. Simon & Freedman (1997) who show how to put priors on interaction terms. Using a Bayesian approach to have an interaction “half in” the model is a much more rational approach than prevailing approaches that
To gain the advantages of Bayesian modeling described above, doing away with binary decisions and allowing the use of outside information, one must specify prior distributions for parameters. It is often difficult to do this, especially when there are nonlinear effects (e.g., splines) and interactions in the model. We need a way to specify priors on the original \(X\) and \(Y\) scales. Fortunately Stan provides an elegant solution.
As discussed here Stan allows one to specify priors on transformations of model parameters, and these priors propagate back to the original parameters. It is easier to specify a prior for the effect of increasing age from 30 to 60 that it is to specify a prior for the age slope. It may be difficult to specify a prior for an age \(\times\) treatment interaction (especially when the age effect is nonlinear), but much easier to specify a prior for how different the treatment effect is for a 30 year old and a 60 year old. By specifying priors on one or more contrasts one can easily encode outside information / information borrowing / shrinkage.
The rms contrast function provides a general way to implement contrasts up to double differences, and more details about computations are provided in that link. The approach used for specifying priors for contrast in rmsb::blrm uses the same process but is even more general. Both contrast and blrm compute design matrices at user-specified predictor settings, and the contrast matrices (matrices multipled by \(\hat{\beta}\)) are simply differences in such design matrices. Thinking of contrasts as differences in predicted values frees the user from having to care about how parameters map to estimands, and allows an R predict(fit, type='x') function do the hard work. Examples of types of differences are below.
rmsb implements priors on contrasts starting with version 1.0-0.blrm for priors)For predictors modeled linearly, the slope is the regression coefficient. For nonlinear effects where \(x\) is transformed by \(f(x)\), the slope at \(x=\frac{a+b}{2}\) is proportionally approximated by \(f(b) - f(a)\), and the slope at \(x=\frac{b+c}{2}\) by \(f(c) - f(b)\). The amount of nonlinearity is reflected by the difference in the two slopes, or \(f(c) - f(b) -[f(b) - f(a)] = f(a) + f(c) - 2f(b)\). You’ll see this form specified in the contrast part of the pcontrast argument to blrm below.
Semiparametic models are introduced in Chapter 13 but we will use one of the models—the proportional odds (PO) ordinal logistic model—in showcasing the utility of specifying priors on contrasts in order to use external information or to place restrictions on model fits. The blrm function in the rmsb package implements this semiparametric model using Stan. Because it does not depend on knowing how to transform \(Y\), I almost always use the more robust ordinal models instead of linear models. The linear predictor \(X\beta\) is on the logit (log odds) scale for the PO model. This unitless scale typically ranges from -5 to 5, corresponding to a range of probabilities of 0.007 to 0.993. Default plotting uses the intercept corresponding to the marginal median of \(Y\), so the log odds of the probability that \(Y\) exceeds or equals this level, given \(X\), is plotted. Estimates can be converted to means, quantiles, or exceedance probabilities using the Mean, Quantile, and ExProb functions in the rms and rmsb packages.
Effects for the PO model are usually expressed as odds ratios (OR). For the case where the prior median for the OR is 1.0 (prior mean or median log(OR)=0.0) it is useful to solve for the prior SD \(\sigma\) so that \(\Pr(\text{OR} > r) = a = \Pr(\text{OR} < \frac{1}{r})\), leading to \(a = \frac{|\log(r)|}{\Phi^{-1}(1-a)}\), computed by the psigma function below. Another function . is defined as an abbreviation for list() for later usage.
psigma <- function(r, a, inline=FALSE, pr=! inline) {
sigma <- abs(log(r)) / qnorm(1 - a)
dir <- if(r > 1.) '>' else '<'
x <- if(inline) paste0('$\\Pr(\\text{OR}', dir, r, ') =', a,
' \\Rightarrow \\sigma=', round(sigma, 3), '$')
else paste0('Pr(OR ', dir, ' ', r, ') = ', a, ' ⇒ σ=', round(sigma, 3))
if(inline) return(x)
if(pr) {
cat('\n', x, '\n\n', sep='')
return(invisible(sigma))
}
sigma
}
. <- function(...) list(...)Start with a simple hypothetical example:
We wish to specify a prior on the treatment effect at age 50 so that there is only a 0.05 chance that the \(\text{OR} < 0.5\). \(\Pr(\text{OR}<0.5) =0.05 \Rightarrow \sigma=0.421\). The covariate settings specified in pcontrast below do not mention sex, so predictions are evaluated at the default sex (the mode). Since sex does not interact with anything, the treatment difference of interest makes the sex setting irrelevant anyway.
Note that the notation needed for pcontrast need not consider how age is modeled.
Consider a more complicated situation. Let’s simulate data for one continuous predictor where the true model is a sine wave. The response variable is a slightly rounded version of a conditionally normal \(Y\).
require(rmsb)
require(ggplot2)
options(mc.cores=4, # See https://hbiostat.org/r/examples/blrm/blrm
rmsb.backend='cmdstan', rmsbdir='~/.rmsb',
prType='html')
cmdstanr::set_cmdstan_path(cmdstan.loc)
# cmdstan.loc is defined in ~/.Rprofile
set.seed(3)
n <- 200
x <- rnorm(n)
y <- round(sin(2*x) + rnorm(n), 1)
dd <- datadist(x, q.display=c(.005, .995)); options(datadist='dd')
f <- blrm(y ~ rcs(x, 6))Running MCMC with 4 parallel chains...
Chain 1 finished in 1.1 seconds.
Chain 2 finished in 1.1 seconds.
Chain 3 finished in 1.1 seconds.
Chain 4 finished in 1.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.1 seconds.
Total execution time: 1.3 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.052 for Intercepts
blrm(formula = y ~ rcs(x, 6))
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 200 | LOO log L -784.58±14.27 | g 1.408 [1.122, 1.724] | C 0.699 [0.689, 0.704] |
| Draws 4000 | LOO IC 1569.17±28.54 | gp 0.294 [0.246, 0.337] | Dxy 0.397 [0.378, 0.408] |
| Chains 4 | Effective p 75.53±6.39 | EV 0.275 [0.19, 0.364] | |
| Time 1.9s | B 0.197 [0.193, 0.203] | v 1.562 [0.87, 2.195] | |
| p 5 | vp 0.068 [0.048, 0.091] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry | |
|---|---|---|---|---|---|---|---|---|
| x | -3.1231 | -3.0875 | -3.0993 | 0.7868 | -4.5816 | -1.5200 | 0.0003 | 1.04 |
| x' | 17.0447 | 16.7737 | 16.6810 | 7.9381 | 1.3943 | 31.8894 | 0.9838 | 1.01 |
| x'' | -20.1489 | -19.1846 | -19.3400 | 37.7108 | -93.7203 | 53.6645 | 0.3058 | 1.00 |
| x''' | -37.4113 | -38.2201 | -37.2322 | 58.6742 | -150.0190 | 77.9698 | 0.2575 | 0.98 |
| x'''' | 50.8032 | 50.3954 | 50.1420 | 50.6961 | -54.9690 | 147.2090 | 0.8440 | 1.02 |
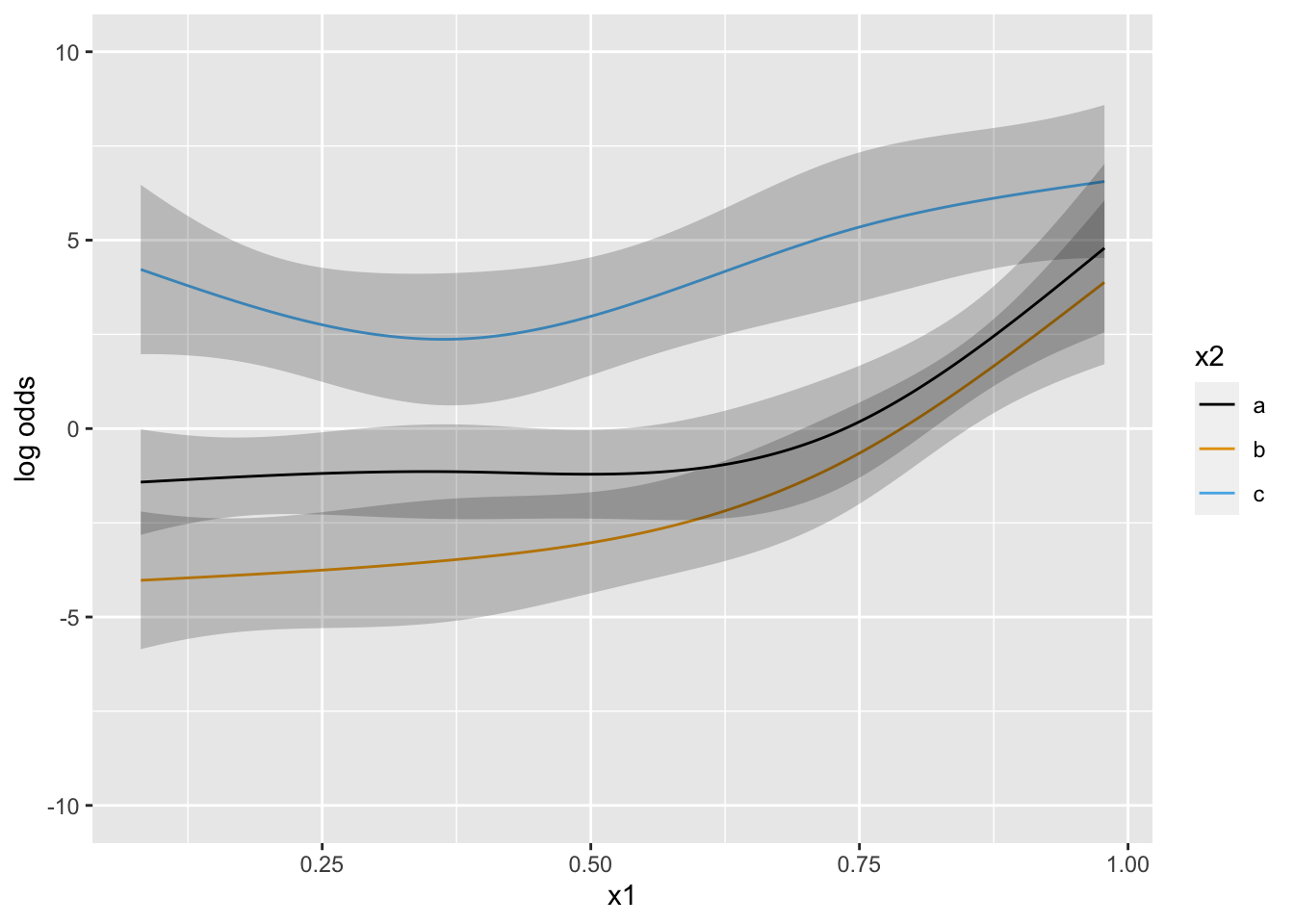
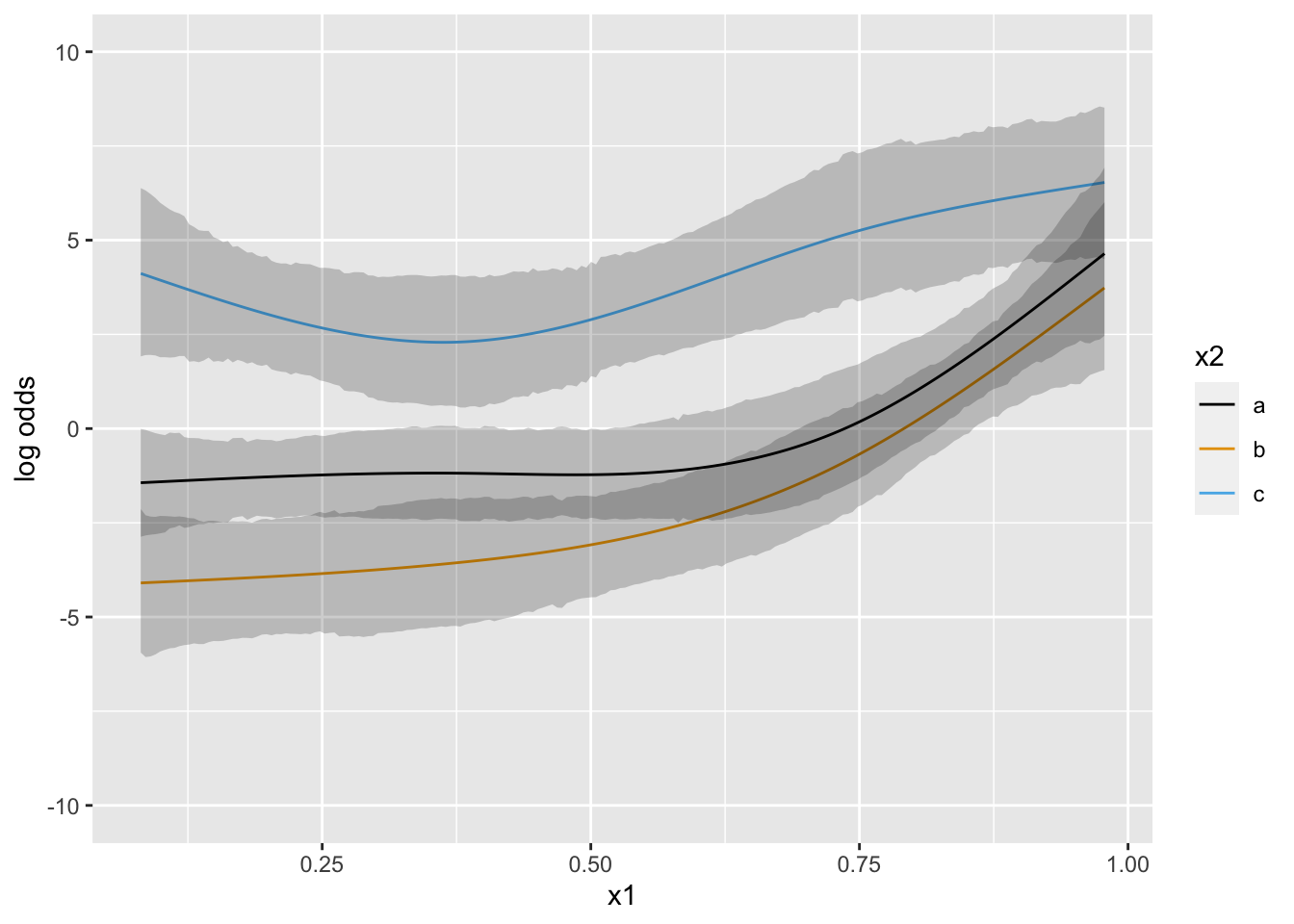
Now suppose that there is strong prior knowledge that the effect of x is linear when x is in the interval \([-1, 0]\). Let’s reflect that by putting a very sharp prior to tilt the difference in slopes within that interval towards 0.0. pcontrast= specifies two separate contrasts to pull towards zero to more finely detect nonlinearity.
Pr(OR > 1.05) = 0.01 ⇒ σ=0.021Running MCMC with 4 parallel chains...
Chain 1 finished in 2.0 seconds.
Chain 2 finished in 2.1 seconds.
Chain 3 finished in 2.1 seconds.
Chain 4 finished in 2.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 2.1 seconds.
Total execution time: 2.3 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.052 for Intercepts
blrm(formula = y ~ rcs(x, 6), pcontrast = con)
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 200 | LOO log L -800.86±15.15 | g 0.938 [0.612, 1.215] | C 0.658 [0.642, 0.676] |
| Draws 4000 | LOO IC 1601.72±30.3 | gp 0.208 [0.139, 0.257] | Dxy 0.316 [0.284, 0.353] |
| Chains 4 | Effective p 74.97±6.69 | EV 0.141 [0.068, 0.205] | |
| Time 2.8s | B 0.214 [0.209, 0.22] | v 0.74 [0.34, 1.187] | |
| p 5 | vp 0.035 [0.017, 0.051] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry | |
|---|---|---|---|---|---|---|---|---|
| x | 0.2739 | 0.2768 | 0.2711 | 0.3175 | -0.3268 | 0.8899 | 0.8040 | 1.05 |
| x' | 1.3743 | 1.3892 | 1.3892 | 0.9284 | -0.3219 | 3.3005 | 0.9312 | 1.03 |
| x'' | -6.0055 | -6.0936 | -6.1744 | 3.5463 | -13.0086 | 0.5510 | 0.0430 | 1.03 |
| x''' | 24.1393 | 24.4599 | 24.5244 | 10.8317 | 2.9317 | 45.3996 | 0.9875 | 1.00 |
| x'''' | -65.1711 | -66.0545 | -66.1233 | 22.2865 | -112.2708 | -24.1124 | 0.0015 | 0.99 |
Contrasts Given Priors
[1] "list(sd = c(0.0209728582358081, 0.0209728582358081), c1 = list("
[2] " x = -1), c2 = list(x = -0.75), c3 = list(x = -0.5), c4 = list("
[3] " x = -0.25), c5 = list(x = 0), contrast = expression(c1 + "
[4] " c3 - 2 * c2, c3 + c5 - 2 * c4))"
rcs(x, 6)x rcs(x, 6)x' rcs(x, 6)x'' rcs(x, 6)x''' rcs(x, 6)x''''
1 0 0.02911963 0.002442679 0.00000000 0
1 0 0.04851488 0.020842754 0.00300411 0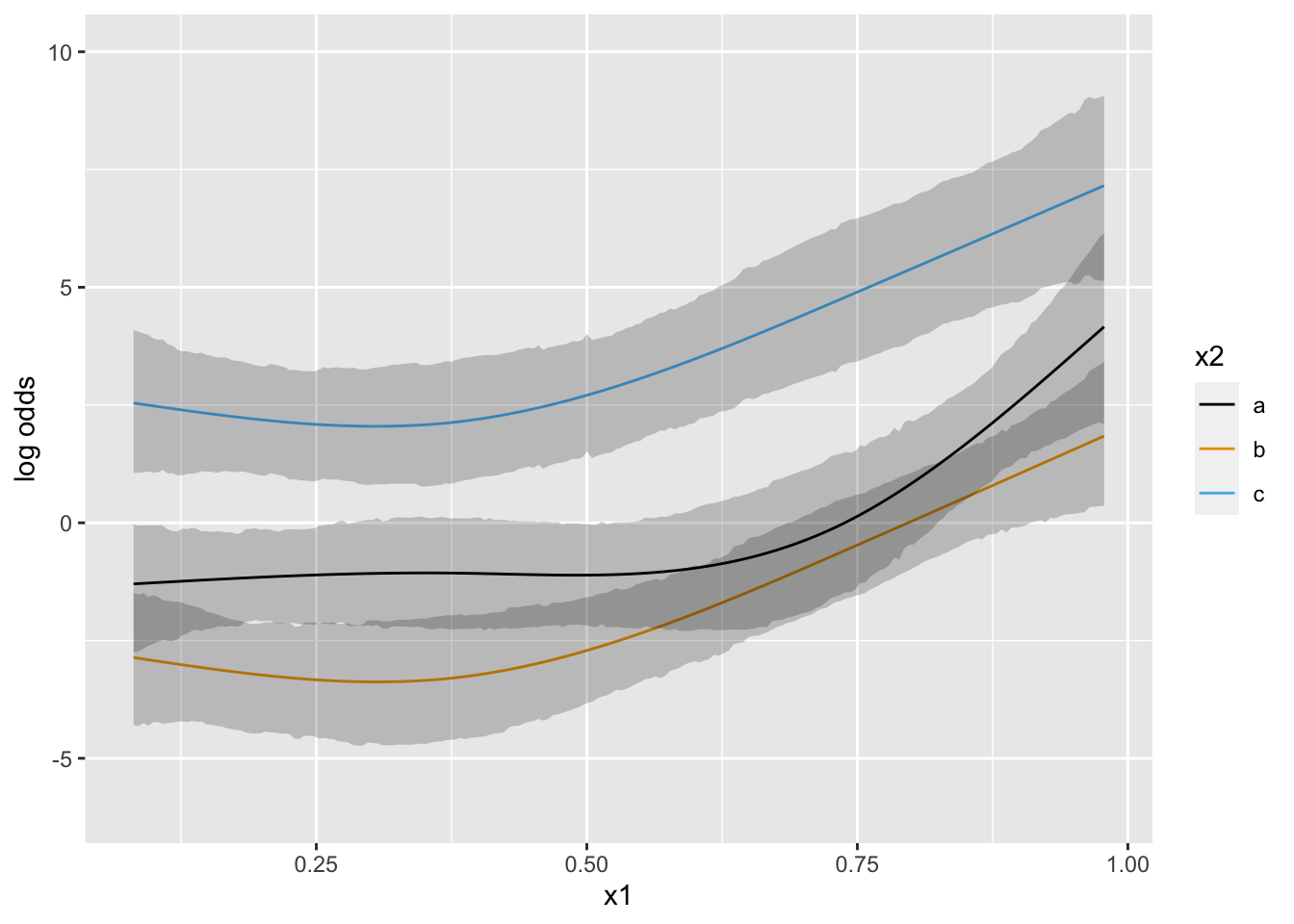
What happens if we moderately limit the acceleration (second derivative; slope of the slope) at 7 equally-spaced points?
con <- list(sd=rep(0.5, 7),
c1=.(x=-2), c2=.(x=-1.5), c3=.(x=-1), c4=.(x=-.5), c5=.(x=0),
c6=.(x=.5), c7=.(x=1), c8=.(x=1.5), c9=.(x=2),
contrast=expression(c1 + c3 - 2 * c2,
c2 + c4 - 2 * c3,
c3 + c5 - 2 * c4,
c4 + c6 - 2 * c5,
c5 + c7 - 2 * c6,
c6 + c8 - 2 * c7,
c7 + c9 - 2 * c8) )
f <- blrm(y ~ rcs(x, 6), pcontrast=con)Running MCMC with 4 parallel chains...
Chain 1 finished in 1.1 seconds.
Chain 2 finished in 1.1 seconds.
Chain 3 finished in 1.1 seconds.
Chain 4 finished in 1.1 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.1 seconds.
Total execution time: 1.3 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.052 for Intercepts
blrm(formula = y ~ rcs(x, 6), pcontrast = con)
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 200 | LOO log L -785.44±13.84 | g 1.055 [0.76, 1.306] | C 0.694 [0.683, 0.703] |
| Draws 4000 | LOO IC 1570.87±27.69 | gp 0.236 [0.179, 0.283] | Dxy 0.388 [0.365, 0.407] |
| Chains 4 | Effective p 73.42±6.32 | EV 0.178 [0.102, 0.252] | |
| Time 1.9s | B 0.198 [0.193, 0.205] | v 0.881 [0.453, 1.328] | |
| p 5 | vp 0.044 [0.025, 0.063] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry | |
|---|---|---|---|---|---|---|---|---|
| x | -2.0431 | -2.0064 | -2.0094 | 0.6091 | -3.2157 | -0.8830 | 0.0010 | 1.01 |
| x' | 12.6728 | 12.4200 | 12.4360 | 4.9966 | 3.0227 | 22.0824 | 0.9942 | 1.01 |
| x'' | -21.0720 | -20.1906 | -20.1671 | 21.8975 | -60.8610 | 23.0118 | 0.1822 | 0.98 |
| x''' | -9.4485 | -10.3232 | -10.2813 | 32.6311 | -75.4638 | 51.1679 | 0.3760 | 0.98 |
| x'''' | 14.4216 | 14.6361 | 14.8242 | 28.5483 | -39.8295 | 71.7553 | 0.6975 | 1.00 |
Contrasts Given Priors
[1] "list(sd = c(0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5), c1 = list(x = -2), "
[2] " c2 = list(x = -1.5), c3 = list(x = -1), c4 = list(x = -0.5), "
[3] " c5 = list(x = 0), c6 = list(x = 0.5), c7 = list(x = 1), c8 = list("
[4] " x = 1.5), c9 = list(x = 2), contrast = expression(c1 + "
[5] " c3 - 2 * c2, c2 + c4 - 2 * c3, c3 + c5 - 2 * c4, c4 + "
[6] " c6 - 2 * c5, c5 + c7 - 2 * c6, c6 + c8 - 2 * c7, c7 + "
[7] " c9 - 2 * c8))"
rcs(x, 6)x rcs(x, 6)x' rcs(x, 6)x'' rcs(x, 6)x''' rcs(x, 6)x''''
1 0 0.01298375 0.000000000 0.000000000 0.000000000
1 0 0.07768802 0.002453429 0.000000000 0.000000000
1 0 0.15526901 0.045575694 0.003046185 0.000000000
1 0 0.23285000 0.122161511 0.048638084 0.001537246
1 0 0.30602473 0.196347206 0.122778948 0.037926277
1 0 0.24969458 0.170741274 0.117781863 0.055476864
1 0 0.06289905 0.043179908 0.029952920 0.014391805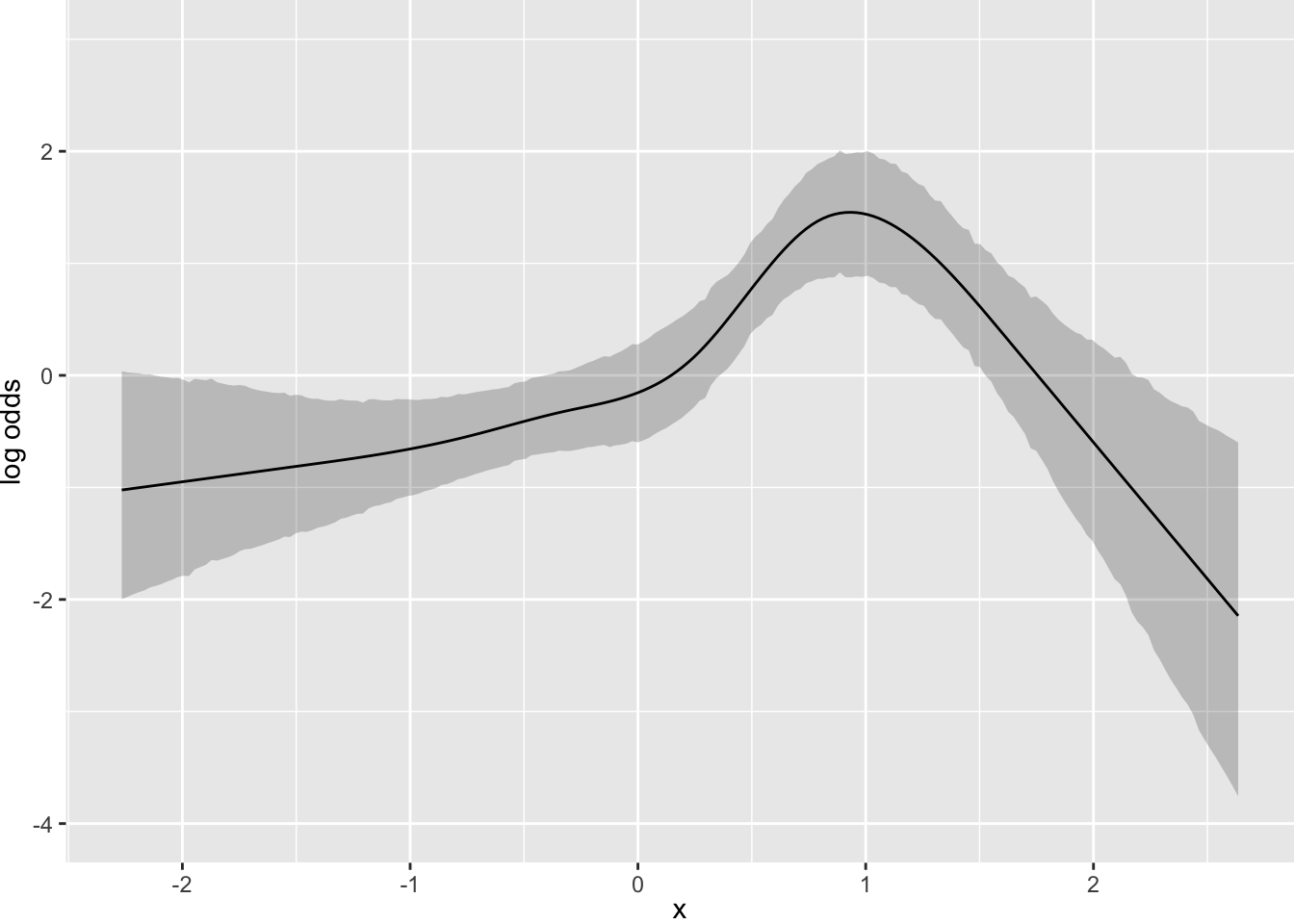
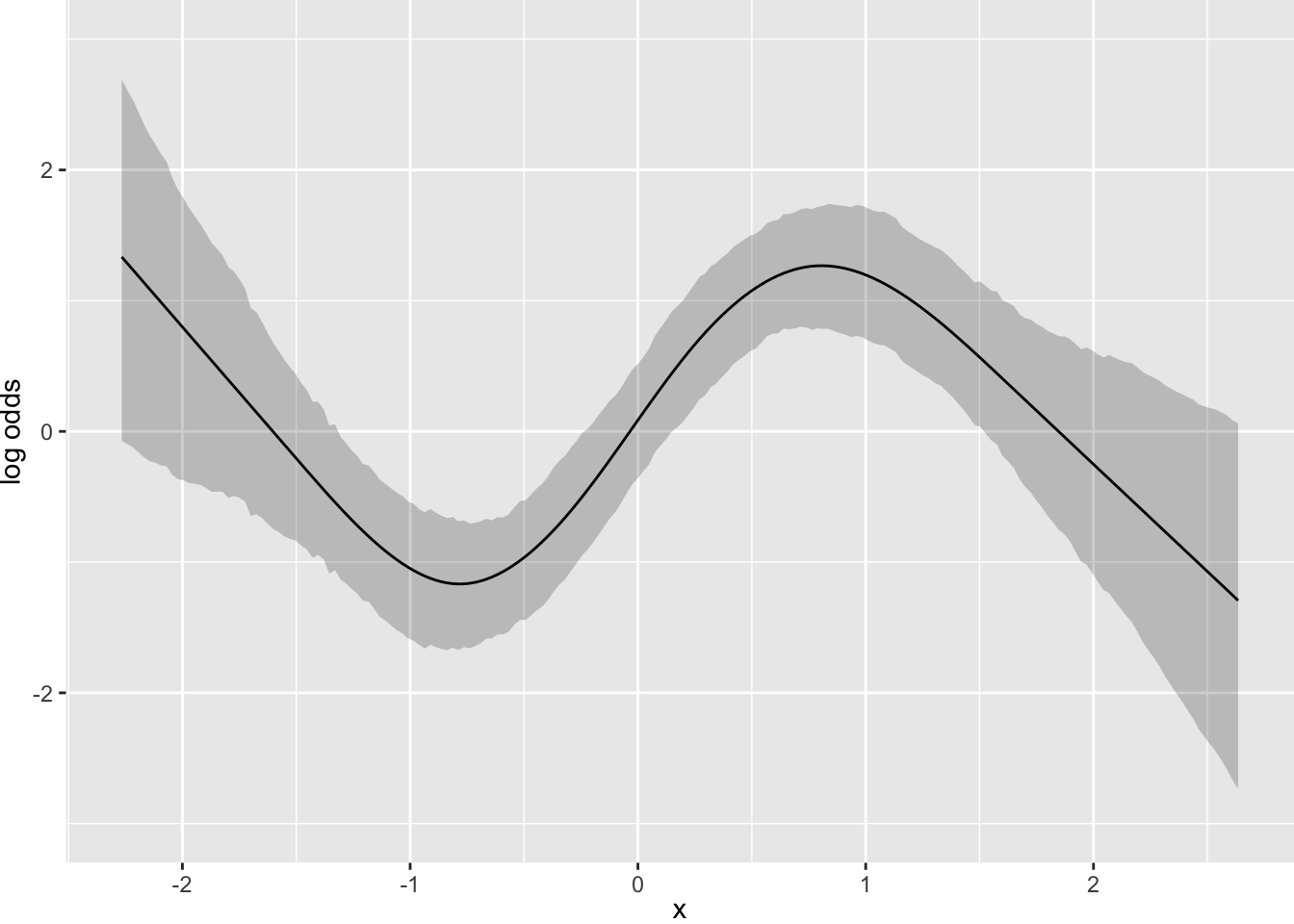
Next simulate data with one continuous predictor x1 and a 3-level grouping variable x2. Start with almost flat priors that allow arbitrary interaction patterns as long as x1 has a smooth effect.
Running MCMC with 4 parallel chains...
Chain 1 finished in 0.5 seconds.
Chain 2 finished in 0.5 seconds.
Chain 3 finished in 0.5 seconds.
Chain 4 finished in 0.5 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.5 seconds.
Total execution time: 0.7 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.105 for Intercepts
blrm(formula = y ~ rcs(x1, 4) * x2)
Frequencies of Responses
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1 1 4 1 2 1 8 5 5 5 4 3 8 3 7 8 3 4 3 3 2 2.1 2.2 2.3 2.7 4 4 1 1 1
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 90 | LOO log L -252.21±9.71 | g 3.805 [2.976, 4.622] | C 0.847 [0.831, 0.86] |
| Draws 4000 | LOO IC 504.42±19.42 | gp 0.439 [0.402, 0.475] | Dxy 0.694 [0.662, 0.721] |
| Chains 4 | Effective p 44.25±4.55 | EV 0.645 [0.52, 0.753] | |
| Time 1.1s | B 0.11 [0.099, 0.124] | v 11.178 [6.965, 16.474] | |
| p 11 | vp 0.159 [0.127, 0.191] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry | |
|---|---|---|---|---|---|---|---|---|
| x1 | 1.5717 | 1.4670 | 1.4227 | 4.8284 | -8.1477 | 10.4985 | 0.6212 | 1.00 |
| x1' | -5.8941 | -5.2274 | -5.2633 | 15.5814 | -36.2680 | 24.0004 | 0.3730 | 1.00 |
| x1'' | 44.1410 | 41.3931 | 41.0002 | 45.6162 | -43.0017 | 133.4448 | 0.8230 | 1.01 |
| x2=b | -2.5975 | -2.6462 | -2.6703 | 1.5552 | -5.6062 | 0.4052 | 0.0440 | 1.01 |
| x2=c | 6.5737 | 6.4544 | 6.4065 | 1.9340 | 2.4277 | 10.0272 | 0.9995 | 1.07 |
| x1 × x2=b | -0.1111 | -0.1173 | -0.0219 | 7.1208 | -14.8468 | 12.9927 | 0.4990 | 1.01 |
| x1' × x2=b | 9.7336 | 9.8530 | 9.7834 | 22.5358 | -35.5647 | 51.3511 | 0.6715 | 1.00 |
| x1'' × x2=b | -28.6458 | -28.8946 | -29.3462 | 64.3363 | -148.0488 | 99.5373 | 0.3252 | 1.00 |
| x1 × x2=c | -11.4703 | -11.1676 | -11.1761 | 8.3933 | -27.3397 | 5.4343 | 0.0922 | 0.98 |
| x1' × x2=c | 39.1979 | 38.0273 | 38.1629 | 25.6380 | -11.6184 | 86.9388 | 0.9265 | 1.00 |
| x1'' × x2=c | -119.1454 | -114.9953 | -115.1432 | 70.8035 | -248.7439 | 23.0708 | 0.0510 | 0.99 |

Put priors specifying that groups b and c have a similar x1-shape (no partial interaction between x1 and b vs. c). contrast below encodes parallelism with respect to b and c.
con <- list(sd=rep(psigma(1.5, 0.05), 4),
c1=.(x1=0, x2='b'), c2=.(x1=0, x2='c'),
c3=.(x1=.25, x2='b'), c4=.(x1=.25, x2='c'),
c5=.(x1=.5, x2='b'), c6=.(x1=.5, x2='c'),
c7=.(x1=.75, x2='b'), c8=.(x1=.75, x2='c'),
c9=.(x1=1, x2='b'), c10=.(x1=1, x2='c'),
contrast=expression(c1 - c2 - (c3 - c4), # gap between b and c curves at x1=0 vs. x1=.25
c1 - c2 - (c5 - c6),
c1 - c2 - (c7 - c8),
c1 - c2 - (c9 - c10) ))
Pr(OR > 1.5) = 0.05 ⇒ σ=0.247Running MCMC with 4 parallel chains...
Chain 1 finished in 1.4 seconds.
Chain 4 finished in 1.5 seconds.
Chain 2 finished in 1.7 seconds.
Chain 3 finished in 1.7 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.6 seconds.
Total execution time: 1.8 seconds.Bayesian Proportional Odds Ordinal Logistic Model
Dirichlet Priors With Concentration Parameter 0.105 for Intercepts
blrm(formula = y ~ rcs(x1, 4) * x2, pcontrast = con)
Frequencies of Responses
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1 1 4 1 2 1 8 5 5 5 4 3 8 3 7 8 3 4 3 3 2 2.1 2.2 2.3 2.7 4 4 1 1 1
| Mixed Calibration/ Discrimination Indexes |
Discrimination Indexes |
Rank Discrim. Indexes |
|
|---|---|---|---|
| Obs 90 | LOO log L -251.91±9.31 | g 3.495 [2.762, 4.204] | C 0.844 [0.831, 0.854] |
| Draws 4000 | LOO IC 503.81±18.62 | gp 0.421 [0.385, 0.459] | Dxy 0.688 [0.661, 0.708] |
| Chains 4 | Effective p 40.18±4.25 | EV 0.574 [0.466, 0.684] | |
| Time 2.3s | B 0.11 [0.098, 0.121] | v 9.59 [5.917, 13.783] | |
| p 11 | vp 0.142 [0.114, 0.172] |
| Mode β | Mean β | Median β | S.E. | Lower | Upper | Pr(β>0) | Symmetry | |
|---|---|---|---|---|---|---|---|---|
| x1 | 1.3876 | 1.2181 | 1.2145 | 4.5045 | -7.6280 | 9.9386 | 0.6070 | 0.99 |
| x1' | -5.3200 | -4.4410 | -4.7942 | 14.5520 | -33.2589 | 22.9488 | 0.3782 | 1.04 |
| x1'' | 39.7331 | 36.5587 | 36.1033 | 42.7940 | -47.5885 | 118.8234 | 0.8030 | 0.98 |
| x2=b | -1.1480 | -1.2230 | -1.2189 | 1.3346 | -3.8009 | 1.4470 | 0.1740 | 1.00 |
| x2=c | 4.2587 | 4.1642 | 4.1738 | 1.4324 | 1.4441 | 7.0167 | 0.9972 | 1.01 |
| x1 × x2=b | -4.8027 | -4.5741 | -4.6454 | 6.0367 | -16.3243 | 7.1596 | 0.2272 | 1.01 |
| x1' × x2=b | 23.4169 | 22.4062 | 22.1372 | 19.0136 | -13.6126 | 60.0876 | 0.8812 | 1.00 |
| x1'' × x2=b | -72.8580 | -69.4456 | -68.5429 | 54.4401 | -173.1625 | 40.4369 | 0.1017 | 1.00 |
| x1 × x2=c | -4.6840 | -4.4292 | -4.5171 | 6.0633 | -16.7221 | 6.9674 | 0.2340 | 0.99 |
| x1' × x2=c | 23.0110 | 21.8363 | 21.7288 | 19.1845 | -14.3978 | 59.0463 | 0.8700 | 1.01 |
| x1'' × x2=c | -72.2092 | -68.2441 | -67.9890 | 54.8744 | -174.4558 | 39.2613 | 0.1070 | 1.01 |
Contrasts Given Priors
[1] "list(sd = c(0.246505282576203, 0.246505282576203, 0.246505282576203, " [2] "0.246505282576203), c1 = list(x1 = 0, x2 = \"b\"), c2 = list(x1 = 0, " [3] " x2 = \"c\"), c3 = list(x1 = 0.25, x2 = \"b\"), c4 = list(x1 = 0.25, " [4] " x2 = \"c\"), c5 = list(x1 = 0.5, x2 = \"b\"), c6 = list(x1 = 0.5, " [5] " x2 = \"c\"), c7 = list(x1 = 0.75, x2 = \"b\"), c8 = list(x1 = 0.75, " [6] " x2 = \"c\"), c9 = list(x1 = 1, x2 = \"b\"), c10 = list(x1 = 1, " [7] " x2 = \"c\"), contrast = expression(c1 - c2 - (c3 - c4), c1 - " [8] " c2 - (c5 - c6), c1 - c2 - (c7 - c8), c1 - c2 - (c9 - c10)))"
rcs(x1, 4)x1 rcs(x1, 4)x1' rcs(x1, 4)x1'' x2b x2c rcs(x1, 4)x1:x2b
1 0 0 0 0 0 -0.25
1 0 0 0 0 0 -0.50
1 0 0 0 0 0 -0.75
1 0 0 0 0 0 -1.00
rcs(x1, 4)x1':x2b rcs(x1, 4)x1'':x2b rcs(x1, 4)x1:x2c rcs(x1, 4)x1':x2c
1 -0.006089308 0.000000000 0.25 0.006089308
1 -0.091848739 -0.002089092 0.50 0.091848739
1 -0.372867191 -0.062281932 0.75 0.372867191
1 -0.879577838 -0.236978793 1.00 0.879577838
rcs(x1, 4)x1'':x2c
1 0.000000000
1 0.002089092
1 0.062281932
1 0.236978793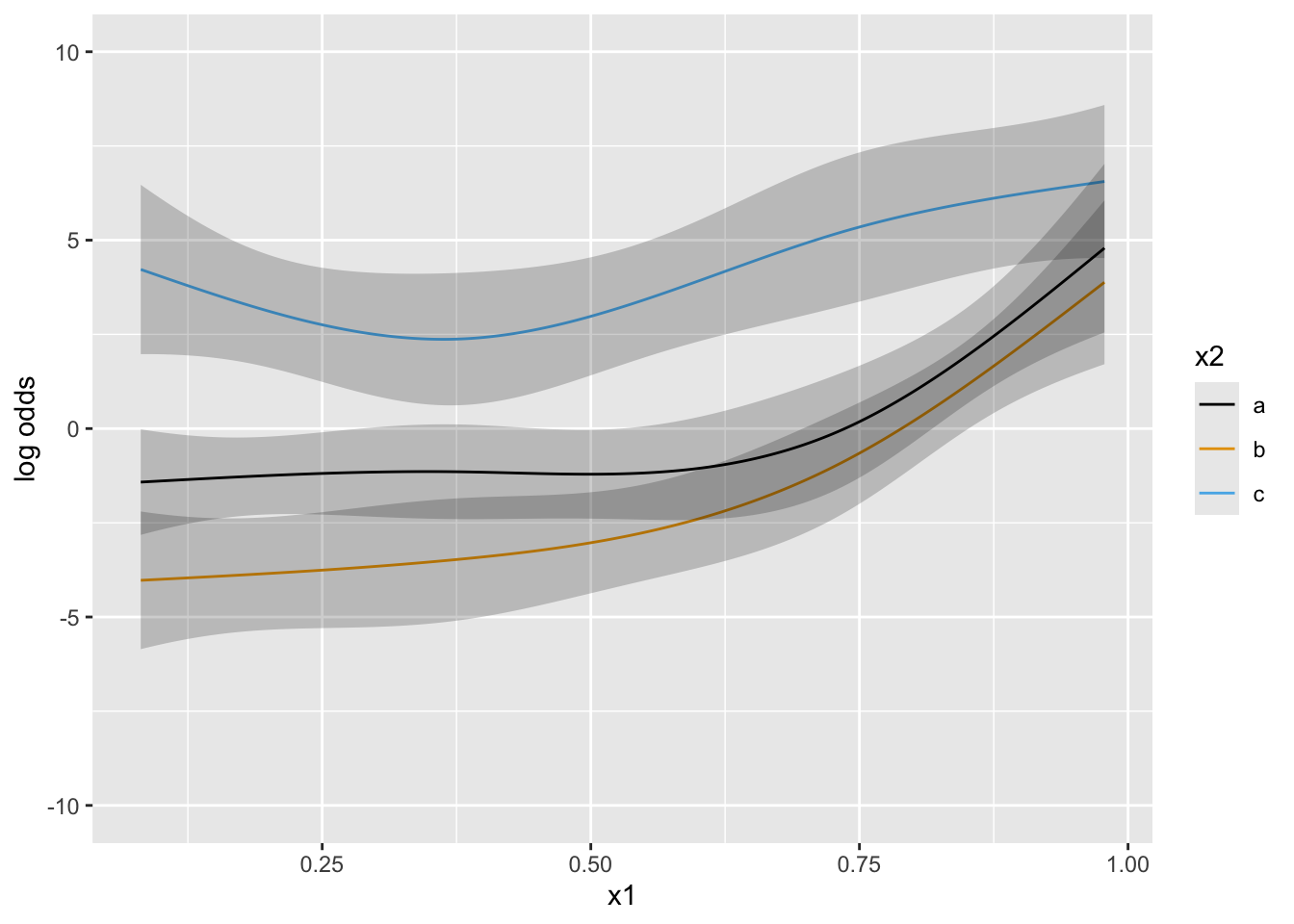
Section 2.1-2.2
Section 2.3
Section 2.4.1
Section 2.4.2
Section 2.5
Section 2.6
Section 2.7.2
```{r include=FALSE}
options(qproject='rms', prType='html')
require(Hmisc)
require(qreport)
getRs('qbookfun.r')
hookaddcap()
knitr::set_alias(w = 'fig.width', h = 'fig.height', cap = 'fig.cap', scap ='fig.scap')
```
# General Aspects of Fitting Regression Models
Regression modeling meets many analytic needs:
`r mrg(sound("genreg-0"))`
* Prediction, capitalizing on efficient estimation methods such as maximum likelihood and the predominant additivity in a variety of problems
+ E.g.: effects of age, smoking, and air quality add to predict lung capacity
+ When effects are predominantly additive, or when there aren't too many interactions and one knows the likely interacting variables in advance, regression can beat machine learning techniques that assume interaction effects are likely to be as strong as main effects
* Isolate effects of variables (especially exposure and treatment)
* Hypothesis testing
* Deep understanding of uncertainties associated with all model components
+ Simplest example: confidence interval for the slope of a predictor
+ Confidence intervals for predicted values; simultaneous confidence intervals for a series of predicted values
- E.g.: confidence band for $Y$ over a series of values of $X$
**Alternative: Stratification**
* Cross-classify subjects on the basis of the $X$s, estimate a property of $Y$ for each stratum
* Only handles a small number of $X$s
* Does not handle continuous $X$
**Alternative: Single Trees (recursive partitioning/CART)**
* Interpretable because they are over-simplified and usually wrong
* Cannot separate effects
* Finds spurious interactions
* Require huge sample size
* Do not handle continuous $X$ effectively; results in very heterogeneous nodes because of incomplete conditioning
* Tree structure is unstable so insights are fragile
**Alternative: Machine Learning**
* E.g. random forests, bagging, boosting, support vector
machines, neural networks, deep learning
* Allows for high-order interactions and does not require pre-specification of interaction terms
* Almost automatic; can save analyst time and do the analysis in one step (long computing time)
* Uninterpretable black box
* Effects of individual predictors are not separable
* Interaction effects (e.g., differential treatment effect = precision medicine = personalized medicine) not available
* Because of not using prior information about dominance of additivity, can require 200 events per candidate predictor when $Y$ is binary (@plo14mod)
+ Logistic regression may require 20 events per candidate predictor
+ Can create a demand for "big data" where additive statistical models can work on moderate-size data
+ See
[this article](https://hbr.org/2016/12/why-youre-not-getting-value-from-your-data-science) in _Harvard Business Review_ for more about
regression vs. complex methods
* Many claims about improved predictive discrimination from ML are exaggerated - see @kap23lea
::: {.column-screen-left}
<img src="images/kap23lea.jpg" width="100%">
:::
## Notation for Multivariable Regression Models
`r mrg(sound("genreg-1"))`
* Weighted sum of a set of independent or predictor variables `r ipacue()`
* Interpret parameters and state assumptions by linearizing
model with respect to regression coefficients
* Analysis of variance setups, interaction effects, nonlinear
effects
* Examining the 2 regression assumptions
| Symbol | Meaning |
|--------|---------|
| $Y$ | response (dependent) variable |
| $X$ | $X_{1},X_{2},\ldots,X_{p}$ -- list of predictors |
| $\beta$ | $\beta_{0},\beta_{1},\ldots,\beta_{p}$ -- regression coefficients |
| $\beta_0$ | intercept parameter(optional) |
| $\beta_{1},\ldots,\beta_{p}$ | weights or regression coefficients |
| $X\beta$ | $\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p}X_{p}, X_{0}=1$ |
Model: connection between $X$ and $Y$ `r ipacue()` <br>
$C(Y|X)$ : property of distribution of $Y$ given $X$, e.g. <br>
$C(Y|X) = {\rm E}(Y|X)$ or $\Pr(Y=1|X)$.
## Model Formulations {#sec-gen.regression.model}
General regression model
$$C(Y|X) = g(X) .$$
General linear regression model
$$C(Y|X) = g(X\beta) .$$
Examples
`r ipacue()`
\begin{array}{ccc}
C(Y|X) =& E(Y|X) =& X\beta, \\
Y|X &\sim N(X\beta,\sigma^{2}) & \\
C(Y|X) =& \Pr(Y=1|X) =& (1+\exp(-X\beta))^{-1} \\
\end{array}
Linearize: $h(C(Y|X))=X\beta,
h(u)=g^{-1}(u)$ <br>
Example: `r ipacue()`
\begin{array}{ccc}
C(Y|X)=\Pr(Y=1|X)&=&(1+\exp(-X\beta))^{-1} \\
h(u)=\mathrm{logit}(u)&=&\log(\frac{u}{1-u}) \\
h(C(Y|X)) &=& C'(Y|X)\ {\rm (link)}
\end{array}
General linear regression model: <br> $C'(Y|X)=X\beta$.
## Interpreting Model Parameters
Suppose that $X_{j}$ is linear and doesn't interact with other
$X$'s^[Note that it is not necessary to "hold constant" all other variables to be able to interpret the effect of one predictor. It is sufficient to hold constant the weighted sum of all the variables other than $X_{j}$. And in many cases it is not physically possible to hold other variables constant while varying one, e.g., when a model contains $X$ and $X^{2}$ (David Hoaglin, personal communication).].
`r ipacue()`
\begin{array}{ccc}
C'(Y|X) &=& X\beta = \beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{p}X_{p} \\
\beta_{j} &=& C'(Y|X_{1}, X_{2}, \ldots, X_{j}+1, \ldots, X_{p}) \\
&-& C'(Y|X_{1}, X_{2}, \ldots, X_{j}, \ldots, X_{p})
\end{array}
Drop $'$ from $C'$ and assume $C(Y|X)$ is property of $Y$ that is
linearly related to weighted sum of $X$'s.
### Nominal Predictors
Nominal (polytomous) factor with $k$ levels : $k-1$ indicator variables.
E.g. $T=J,K,L,M$:
`r ipacue()`
\begin{array}{ccc}
C(Y|T=J) &=& \beta_{0} \nonumber\\
C(Y|T=K) &=& \beta_{0}+\beta_{1}\\
C(Y|T=L) &=& \beta_{0}+\beta_{2}\nonumber\\
C(Y|T=M) &=& \beta_{0}+\beta_{3}\nonumber .
\end{array}
$$C(Y|T) = X\beta= \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3} X_{3},$$
where
\begin{array}{ccc}
X_{1} = 1 & {\rm if} \ \ T=K, & 0 \ \ {\rm otherwise} \nonumber\\
X_{2} = 1 & {\rm if} \ \ T=L, & 0 \ \ {\rm otherwise} \\
X_{3} = 1 & {\rm if} \ \ T=M, & 0 \ \ {\rm otherwise} \nonumber.
\end{array}
The test for any differences in the property $C(Y)$ between
treatments is $H_{0}:\beta_{1}=\beta_{2}=\beta_{3}=0$.
### Interactions
`r ipacue()`
$X_{1}$ and $X_{2}$, effect of $X_{1}$ on $Y$ depends on level of $X_{2}$.
_One_ way to describe interaction is to add $X_{3}=X_{1}X_{2}$ to model:
$$C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{1}X_{2} .$$
\begin{array}{ccc}
C(Y|X_{1}+1, X_{2})&-&C(Y|X_{1}, X_{2})\nonumber\\
&=&\beta_{0}+\beta_{1} (X_{1}+1)+\beta_{2}X_{2}\nonumber\\
&+&\beta_{3} (X_{1}+1)X_{2}\\
&-&[\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{1}X_{2}]\nonumber\\
&=&\beta_{1}+\beta_{3}X_{2} .\nonumber
\end{array}
One-unit increase in $X_{2}$ on $C(Y|X)$ :
$\beta_{2}+\beta_{3} X_{1}$.
Worse interactions:
If $X_{1}$ is binary, the interaction may take the form of a difference in shape (and/or distribution) of $X_{2}$ vs. $C(Y)$
depending on whether $X_{1}=0$ or $X_{1}=1$ (e.g. logarithm vs. square root).
[This paper](http://yiqingxu.org/papers/english/2018_HMX_interaction/main.pdf) describes how interaction effects can be misleading. See [Interaction effects need interaction controls](https://datacolada.org/80) by Uri Simonsohn for an explanation of the possible need for controlling for other interactions when the interest is on a specific interaction. <!-- NEW -->
### Example: Inference for a Simple Model
`r mrg(sound("genreg-2"))`
Postulate the model $C(Y|age,sex) = \beta_{0}+\beta_{1} age + \beta_{2}
[sex=f] + \beta_{3} age [sex=f]$ where $[sex=f]$ is an indicator indicator
variable for sex=female, i.e., the reference cell is
sex=male^[You can also think of the last part of the model as being $\beta_{3} X_{3}$, where $X_{3} = age \times [sex=f]$.].
Model assumes
1. age is linearly related to $C(Y)$ for males, `r ipacue()`
1. age is linearly related to $C(Y)$ for females, and
1. interaction between age and sex is simple
1. whatever distribution, variance, and independence assumptions are
appropriate for the model being considered.
Interpretations of parameters: `r ipacue()`
| Parameter | Meaning |
|-----|-----|
| $\beta_{0}$ | $C(Y | age=0, sex=m)$ |
| $\beta_{1}$ | $C(Y | age=x+1, sex=m) - C(Y | age=x, sex=m)$ |
| $\beta_{2}$ | $C(Y | age=0, sex=f) - C(Y | age=0, sex=m)$ |
| $\beta_{3}$ | $C(Y | age=x+1, sex=f) - C(Y | age=x, sex=f) -$ |
| | $[C(Y | age=x+1, sex=m) - C(Y | age=x, sex=m)]$ |
$\beta_{3}$ is the difference in slopes (female -- male).
When a high-order effect such as an interaction effect is in the
model, be sure to interpret low-order effects by finding out what
makes the interaction effect ignorable. In our example, the
interaction effect is zero when age=0 or sex is male.
Hypotheses that are usually inappropriate:
1. $H_{0}: \beta_{1}=0$: This tests whether age is associated with $Y$ for `r ipacue()`
males
1. $H_{0}: \beta_{2}=0$: This tests whether sex is associated with $Y$ for
zero year olds
More useful hypotheses follow. For any hypothesis need to
* Write what is being tested `r ipacue()`
* Translate to parameters tested
* List the alternative hypothesis
* Don't forget what the test is powered to detect
+ Test against nonzero slope has maximum power when linearity holds
+ If true relationship is monotonic, test for non-flatness will
have some but not optimal power
+ Test against a quadratic (parabolic) shape will have some
power to detect a logarithmic shape but not against a sine wave
over many cycles
* Useful to write e.g. "$H_{a}:$ age is associated with
$C(Y)$, powered to detect a _linear_ relationship"
**Most Useful Tests for Linear age $\times$ sex Model**
`r ipacue()`
| Null or Alternative Hypothesis | Mathematical Statement |
|-----|-----|
| Effect of age is independent of sex or<br>Effect of sex is independent of age or<br>age and sex are additive<br>age effects are parallel | $H_{0}: \beta_{3}=0$ |
| age interacts with sex<br>age modifies effect of sex<br>sex modifies effect of age<br>sex and age are non-additive (synergistic) | $H_{a}: \beta_{3} \neq 0$ |
| age is not associated with $Y$ | $H_{0}: \beta_{1}=\beta_{3}=0$ |
| age is associated with $Y$<br>age is associated with $Y$ for either females or males | $H_{a}: \beta_{1} \neq 0 \textrm{~or~} \beta_{3} \neq 0$ |
| sex is not associated with $Y$ | $H_{0}: \beta_{2}=\beta_{3}=0$ |
| sex is associated with $Y$<br>sex is associated with $Y$ for some value of age| $H_{a}: \beta_{2} \neq 0 \textrm{~or~} \beta_{3} \neq 0$ |
| Neither age nor sex is associated with $Y$ | $H_{0}: \beta_{1}=\beta_{2}=\beta_{3}=0$ |
| Either age or sex is associated with $Y$ | $H_{a}: \beta_{1} \neq 0 \textrm{~or~} \beta_{2} \neq 0 \textrm{~or~} \beta_{3} \neq 0$|
**Note**: The last test is called the global test of no
association. If an interaction effect is present, there is
both an age and a sex effect. There can also be age or sex
effects when the lines are parallel. The global test of
association (test of total association) has 3 d.f. instead of 2
(age + sex) because it allows for unequal slopes.
### Review of Composite (Chunk) Tests
* In the model `r ipacue()`
```{r eval=FALSE}
y ~ age + sex + weight + waist + tricep
```
we may want to jointly test the association between all body
measurements and response, holding `age` and `sex` constant.
* This 3 d.f. test may be obtained two ways:
+ Remove the 3 variables and compute the change in $SSR$ or $SSE$
+ Test $H_{0}:\beta_{3}=\beta_{4}=\beta_{5}=0$ using matrix
algebra (e.g., `anova(fit, weight, waist, tricep)` if `fit`
is a fit object created by the `R` `rms` package)
## Relaxing Linearity Assumption for Continuous Predictors {#sec-relax.linear}
### Avoiding Categorization
`r mrg(sound("genreg-3"))`
`r quoteit("Natura non facit saltus<br>(Nature does not make jumps)", "Gottfried Wilhelm Leibniz")`
<img src="images/lucy.png" width="45%"> Lucy D'Agostino McGowan
* Relationships seldom linear except when predicting one variable `r ipacue()`
from itself measured earlier
* Categorizing continuous predictors into intervals is a
disaster; see
@roy06dic, @alt91cat, @hil96pra, @lau96eva, @alt94dan,
@bel92con, @far96sim, @rag92dic, @sui95bin, @bue97pro,
@max93biv, @sch94out, @alt98sub, @hol04con, @mos04odd,
@wai06fin, @fed09con, @gia14opt, @col16qua, @ben12qua
and [Biostatistics for Biomedical Research](https://hbiostat.org/bbr), Chapter 18.
`r mrg(movie("https://youtu.be/-GEgR71KtwI"))`
* Some problems caused by this approach:
1. Estimated values have reduced
precision, and associated tests have reduced power
1. Categorization assumes relationship between predictor and
response is flat within intervals; far less reasonable than a
linearity assumption in most cases
1. To make a continuous predictor be more accurately modeled when
categorization is used, multiple intervals are required
1. Because of sample size limitations in the very low and very high
range of the variable, the outer intervals (e.g., outer quintiles)
will be wide, resulting in significant heterogeneity of subjects
within those intervals, and residual confounding
1. Categorization assumes that there is a discontinuity in response
as interval boundaries are crossed. Other than the effect of time
(e.g., an instant stock price drop after bad news), there are very
few examples in which such discontinuities have been shown to exist.
1. Categorization only appears to yield interpretable estimates.
E.g. odds ratio for stroke for persons with a systolic blood
pressure $> 160$ mmHg compared to persons with a blood pressure
$\leq 160$ mmHg $\rightarrow$ interpretation of OR depends on
distribution of blood pressures in the sample (the proportion of
subjects $> 170$, $> 180$, etc.). If blood pressure
is modeled as a continuous variable (e.g., using a regression
spline, quadratic, or linear effect) one can estimate the ratio of
odds for _exact_ settings of the predictor, e.g., the odds ratio for
200 mmHg compared to 120 mmHg.
1. Categorization does not condition on full information. When,
for example, the risk of stroke is being assessed for a new subject
with a known blood pressure (say 162~mmHg), the subject does not report
to her physician "my blood pressure exceeds 160" but rather reports
162 mmHg. The risk for this subject will be much lower than that of
a subject with a blood pressure of 200 mmHg.
1. If cutpoints are determined in a way that is not blinded to the
response variable, calculation of $P$-values and confidence
intervals requires special simulation techniques; ordinary
inferential methods are completely invalid. E.g.:
cutpoints chosen by trial and error utilizing $Y$, even informally
$\rightarrow$ $P$-values too small and CLs not accurate^[If a cutpoint is chosen that minimizes the $P$-value and the resulting $P$-value is 0.05, the true type I error can easily be above 0.5 @hol04con.].
1. Categorization not blinded to $Y$ $\rightarrow$ biased effect
estimates (@alt94dan, @sch94out)
1. "Optimal" cutpoints do not replicate over studies.
@hol04con state that "... the optimal
cutpoint approach has disadvantages. One of these is that in almost
every study where this method is applied, another cutpoint will
emerge. This makes comparisons across studies extremely difficult or
even impossible. Altman et al. point out this problem for studies
of the prognostic relevance of the S-phase fraction in breast cancer
published in the literature. They identified 19 different cutpoints
used in the literature; some of them were solely used because they
emerged as the 'optimal' cutpoint in a specific data set. In a
meta-analysis on the relationship between cathepsin-D content and
disease-free survival in node-negative breast cancer patients, 12
studies were in included with 12 different cutpoints \ldots
Interestingly, neither cathepsin-D nor the S-phase fraction are
recommended to be used as prognostic markers in breast cancer in the
recent update of the American Society of Clinical Oncology."
@gia14opt demonstrated that many claimed
"optimal cutpoints" are just the observed median values in the
sample, which happens to optimize statistical power for detecting a
separation in outcomes.
1. Disagreements in cutpoints (which are bound to happen whenever one
searches for things that do not exist) cause severe interpretation
problems. One study may provide an odds
ratio for comparing body mass index (BMI) $> 30$ with BMI $\leq 30$,
another for comparing BMI $> 28$ with BMI $\leq 28$. Neither of these has
a good definition and the two estimates are not comparable.
1. Cutpoints are arbitrary and manipulable; cutpoints can be
found that can result in both positive and negative
associations @wai06fin.
1. If a confounder is adjusted for by categorization, there will be
residual confounding that can be explained away by inclusion of the
continuous form of the predictor in the model in addition to the
categories.
* To summarize: The use of a (single) cutpoint $c$ makes many
assumptions, including: `r ipacue()`
1. Relationship between $X$ and $Y$ is discontinuous at $X=c$ and
only $X=c$
1. $c$ is correctly found as _the_ cutpoint
1. $X$ vs. $Y$ is flat to the left of $c$
1. $X$ vs. $Y$ is flat to the right of $c$
1. The choice of $c$ does not depend on the values of other predictors
Interactive demonstration of power loss of categorization vs.
straight line and quadratic fits in OLS, with varying degree of
nonlinearity and noise added to $X$ (must run in `RStudio`)
`r mrg(movie("https://youtu.be/Q6snkhhTPnQM"))`
[Interactive demonstration](https://apps.biostat.au.dk/stefan/splines/) of lack of fit after categorization of a continuous predictor, and comparison with spline fits, by Stefan Hansen
```{r eval=FALSE}
require(Hmisc)
# Install the manipulate package to make catgNoise work
getRs('catgNoise.r')
```
Example^[From NHANES III; Diabetes Care 32:1327-34; 2009 adapted from Diabetes Care 20:1183-1197; 1997.] of misleading results from creating intervals (here, deciles) of a continuous predictor. Final interval is extremely heterogeneous and is greatly influenced by very large glycohemoglobin values, creating the false impression of an inflection point at 5.9.
<img src="images/nhanesIIIretinopathy.png" width="90%">
See [this](https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-12-21) for excellent graphical examples of the harm of categorizing predictors, especially when using quantile groups.
### Simple Nonlinear Terms
`r mrg(sound("genreg-4"))`
$$C(Y|X_{1}) = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{1}^{2} .$$
* $H_{0}:$ model is linear in $X_{1}$ vs. $H_{a}:$ model is `r ipacue()`
quadratic in $X_{1} \equiv H_{0}: \beta_{2}=0$.
* Test of linearity may be powerful if true model is not extremely
non-parabolic
* Predictions not accurate in general as many phenomena are
non-quadratic
* Can get more flexible fits by adding powers higher than 2
* But polynomials do not adequately fit logarithmic functions or
"threshold" effects, and have unwanted peaks and valleys.
### Splines for Estimating Shape of Regression Function and Determining Predictor Transformations
* <b>Draftsman's _spline_</b>: flexible strip of metal or rubber used to `r ipacue()`
trace curves.
* **_Spline Function_**: piecewise polynomial[See [this](https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-019-0666-3) for a nice review and information about resources in R.]{.aside}
* **_Linear Spline Function_**: piecewise linear function
+ Bi-linear regression: model is $\beta_{0}+\beta_{1}X$ if $X \leq a$, $\beta_{2}+\beta_{3}X$ if $X > a$.
+ Problem with this notation: two lines not constrained to join
+ To force simple continuity: $\beta_{0} + \beta_{1}X +
\beta_{2}(X-a)\times [X>a] = \beta_{0} + \beta_{1}X_{1} +
\beta_{2}X_{2}$,<br>where $X_{2} = (X_{1}-a) \times [X_{1} > a]$.
+ Slope is $\beta_{1}, X \leq a$, $\beta_{1}+\beta_{2}, X > a$.
+ $\beta_{2}$ is the slope increment as you pass $a$
More generally: $x$-axis divided into intervals with endpoints $a,b,c$
(knots).
\begin{array}{ccc}
f(X) &=& \beta_{0}+\beta_{1}X+\beta_{2}(X-a)_{+}+\beta_{3}(X-b)_{+} \nonumber\\
&+& \beta_{4}(X-c)_{+} ,
\end{array}
where
\begin{array}{ccc}
(u)_{+}=&u,&u>0 ,\nonumber\\
&0,&u\leq0 .
\end{array}
`r ipacue()`
\begin{array}{ccc}
f(X) & = \beta_{0}+\beta_{1}X, & X\leq a \nonumber \\
& = \beta_{0}+\beta_{1}X+\beta_{2}(X-a) & a<X\leq b \\
& = \beta_{0}+\beta_{1}X+\beta_{2}(X-a)+\beta_{3}(X-b) & b<X\leq c \nonumber\\
& = \beta_{0}+\beta_{1}X+\beta_{2}(X-a) & \nonumber\\
& + \beta_{3}(X-b)+\beta_{4}(X-c) & c<X. \nonumber
\end{array}
```{r lspline2,echo=FALSE,cap='A linear spline function with knots at $a = 1, b = 3, c = 5$.'}
#| label: fig-gen-lspline
spar(bty='l')
x <- c(0,1,3,5,6)
y <- c(4,3,5.5,5,2)
plot(x, y, type="l", xlab=expression(X), ylab=expression(f(X)), axes=FALSE)
axis(1)
axis(2, labels=FALSE)
```
$$C(Y|X) = f(X) = X\beta,$$
where $X\beta = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3}X_{3}+\beta_{4} X_{4}$, and
\begin{array}{cc}
X_{1}=X & X_{2} = (X-a)_{+}\nonumber\\
X_{3}=(X-b)_{+} & X_{4} = (X-c)_{+} .
\end{array}
Overall linearity in $X$ can
be tested by testing $H_{0} : \beta_{2} = \beta_{3} = \beta_{4} = 0$.
### Cubic Spline Functions
Cubic splines are smooth at knots (function, first and second derivatives
agree) --- can't see joins.
`r ipacue()`
\begin{array}{ccc}
f(X) &=& \beta_{0}+\beta_{1}X+\beta_{2}X^{2}+\beta_{3}X^{3}\nonumber\\
&+&\beta_{4}(X-a)_{+}^{3}+ \beta_{5}(X-b)_{+}^{3}+\beta_{6}(X-c)_{+}^{3}\\
&=& X\beta\nonumber
\end{array}
\begin{array}{cc}
X_{1}=X & X_{2}=X^{2}\nonumber\\
X_{3}=X^{3} & X_{4}=(X-a)_{+}^{3}\\
X_{5}=(X-b)_{+}^{3} & X_{6}=(X-c)_{+}^{3}\nonumber .
\end{array}
$k$ knots $\rightarrow k+3$ coefficients excluding intercept.
$X^2$ and $X^3$ terms must be included to allow nonlinearity when $X < a$.
[stats.stackexchange.com/questions/421964](https://stats.stackexchange.com/questions/421964)
has some useful descriptions of what happens at the knots, e.g.:
Knots are where different cubic polynomials are joined, and
cubic splines force there to be three levels of continuity (the
function, its slope, and its acceleration or second derivative
(slope of the slope) do not change) at these points. At the knots
the jolt (third derivative or rate of change of acceleration) is
allowed to change suddenly, meaning the jolt is allowed to be
discontinuous at the knots. Between knots, jolt is constant.
The following graphs show the function and its first three derivatives
(all further derivatives are zero) for the function given by
$f(x) = x + x^{2} + 2x^{3} + 10(x - 0.25)^{3}_{+} - 50(x - 0.5)^{3}_{+} -100(x - 0.75)^{3}_{+}$ for $x$ going from 0 to 1, where there are three knots, at $x=0.25, 0.5, 0.75$.
```{r splinederivs,h=6.5,w=4,cap="A regular cubic spline function with three levels of continuity that prevent the human eye from detecting the knots. Also shown is the function's first three derivatives. Knots are located at $x=0.25, 0.5, 0.75$. For $x$ beyond the outer knots, the function is not restricted to be linear. Linearity would imply an acceleration of zero. Vertical lines are drawn at the knots.",scap="Cubic spline function and its derivatives"}
#| label: fig-gen-splinederivs
spar(bty='l', mfrow=c(4,1), bot=-1.5)
x <- seq(0, 1, length=500)
x1 <- pmax(x - .25, 0)
x2 <- pmax(x - .50, 0)
x3 <- pmax(x - .75, 0)
b1 <- 1; b2 <- 1; b3 <- 2; b4 <- 10; b5 <- -50; b6 <- -100
y <- b1 * x + b2 * x^2 + b3 * x^3 + b4 * x1^3 + b5 * x2^3 + b6 * x3^3
y1 <- b1 + 2*b2*x + 3*b3*x^2 + 3*b4*x1^2 + 3*b5*x2^2 + 3*b6*x3^2
y2 <- 2*b2 + 6*b3*x + 6*b4*x1 + 6*b5*x2 + 6*b6*x3
y3 <- 6*b3 + 6*b4*(x1>0)+ 6*b5*(x2>0) + 6*b6*(x3>0)
g <- function() abline(v=(1:3)/4, col=gray(.85))
plot(x, y, type='l', ylab=''); g()
text(0, 1.5, 'Function', adj=0)
plot(x, y1, type='l', ylab=''); g()
text(0, -15, 'First Derivative: Slope\nRate of Change of Function',
adj=0)
plot(x, y2, type='l', ylab=''); g()
text(0, -125, 'Second Derivative: Acceleration\nRate of Change of Slope',
adj=0)
plot(x, y3, type='l', ylab=''); g()
text(0, -400, 'Third Derivative: Jolt\nRate of Change of Acceleration',
adj=0)
```
### Restricted Cubic Splines {#sec-rcspline}
`r mrg(sound("genreg-5"))`
`r ipacue()`
@sto85add: cubic splines poorly behaved in tails.
Constrain function to be linear in tails. <br>
$k+3 \rightarrow k-1$ parameters @dev86spl.
To force linearity when $X < a$: $X^2$ and $X^3$ terms must be omitted
<br>
To force linearity when $X$ is beyond the last knot: last two $\beta$ s are
redundant, i.e., are just combinations of the other $\beta$ s.
The restricted spline function with $k$ knots $t_{1}, \ldots, t_{k}$
is given by @dev86spl
$$f(X) = \beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\ldots+\beta_{k-1} X_{k-1},$$
where $X_{1} = X$ and for $j=1, \ldots, k-2$,
`r ipacue()`
$$\begin{array}{ccc}
X_{j+1} &= &(X-t_{j})_{+}^{3}-(X-t_{k-1})_{+}^{3} (t_{k}-t_{j})/(t_{k}-t_{k-1})\nonumber\\
&+&(X-t_{k})_{+}^{3} (t_{k-1}-t_{j})/(t_{k}-t_{k-1}).
\end{array}$$ {#eq-rcspline-eq}
$X_{j}$ is linear in $X$ for $X\geq t_{k}$.
For numerical behavior and to put all basis functions for $X$ on the
same scale, `R` `Hmisc` and `rms` package functions by default
divide the terms above by $\tau = (t_{k} - t_{1})^{2}$.
```{r rcscomp,h=3.5,w=4.5,cap='Restricted cubic spline component variables for $k = 5$ and knots at $X = .05, .275, .5, .725$, and $.95$. Nonlinear basis functions are scaled by $\\tau$. The left panel is a $y$--magnification of the right panel. Fitted functions such as those in @fig-gen-rcsex will be linear combinations of these basis functions as long as knots are at the same locations used here.',scap='Restricted cubic spline component variables for 5 knots'}
#| label: fig-gen-rcscomp
require(Hmisc)
spar(mfrow=c(1,2), left=-2)
x <- rcspline.eval(seq(0,1,.01),
knots=seq(.05,.95,length=5), inclx=T)
xm <- x
xm[xm > .0106] <- NA
matplot(x[,1], xm, type="l", ylim=c(0,.01),
xlab=expression(X), ylab='', lty=1)
matplot(x[,1], x, type="l",
xlab=expression(X), ylab='', lty=1)
```
```{r rcsex,h=6,w=5.5,cap='Some typical restricted cubic spline functions for $k = 3, 4, 5, 6$. The $y$--axis is $X\\beta$. Arrows indicate knots. These curves were derived by randomly choosing values of $\\beta$ subject to standard deviations of fitted functions being normalized.',scap='Some typical restricted cubic spline functions'}
#| label: fig-gen-rcsex
spar(left=-2, bot=2, mfrow=c(2,2), ps=13)
x <- seq(0, 1, length=300)
for(nk in 3:6) {
set.seed(nk)
knots <- seq(.05, .95, length=nk)
xx <- rcspline.eval(x, knots=knots, inclx=T)
for(i in 1 : (nk - 1))
xx[,i] <- (xx[,i] - min(xx[,i])) /
(max(xx[,i]) - min(xx[,i]))
for(i in 1 : 20) {
beta <- 2*runif(nk-1) - 1
xbeta <- xx %*% beta + 2 * runif(1) - 1
xbeta <- (xbeta - min(xbeta)) /
(max(xbeta) - min(xbeta))
if(i == 1) {
plot(x, xbeta, type="l", lty=1,
xlab=expression(X), ylab='', bty="l")
title(sub=paste(nk,"knots"), adj=0, cex=.75)
for(j in 1 : nk)
arrows(knots[j], .04, knots[j], -.03,
angle=20, length=.07, lwd=1.5)
}
else lines(x, xbeta, col=i)
}
}
```
Interactive demonstration of linear and cubic spline fitting, plus
ordinary $4^{th}$ order polynomial. This can be run with
`RStudio` or in an ordinary `R` session.
`r mrg(movie("https://youtu.be/o_d4hmKhmsQ"))`
```{r eval=FALSE}
require(Hmisc)
getRs('demoSpline.r', put='rstudio') # to see code in RStudio window
getRs('demoSpline.r') # to just run the code
```
Paul Lambert's excellent self-contained interactive demonstrations of
continuity restrictions, cubic polynomial, linear spline, cubic
spline, and restricted cubic spline fitting is at
[pclambert.net/interactive_graphs](https://pclambert.net/interactive_graphs.html).
Jordan Gauthier
has another nice interactive demonstration at [drjgauthier.shinyapps.io/spliny](https://drjgauthier.shinyapps.io/spliny). [See also the excellent resources from Michael Clark [here](https://m-clark.github.io/workshops/stars/building-up-to-gams.html) and [here](https://m-clark.github.io/workshops/stars/technical-details.html#technical-details).]{.aside}
Once $\beta_{0}, \ldots, \beta_{k-1}$ are estimated, the restricted
cubic spline can be restated in the form
`r ipacue()`
$$\begin{array}{ccc}
f(X) &=& \beta_{0}+\beta_{1}X+\beta_{2}(X-t_{1})_{+}^{3}+\beta_{3}(X-t_{2})_{+}^{3}\nonumber\\
&& +\ldots+ \beta_{k+1}(X-t_{k})_{+}^{3}
\end{array}$$ {#eq-rcspline-restate}
by dividing $\beta_{2},\ldots,\beta_{k-1}$ by $\tau$ and computing
\begin{array}{ccc}
\beta_{k} &=&
[\beta_{2}(t_{1}-t_{k})+\beta_{3}(t_{2}-t_{k})+\ldots\nonumber\\
&& +\beta_{k-1}(t_{k-2}-t_{k})]/(t_{k}-t_{k-1})\nonumber\\
\beta_{k+1} &= &
[\beta_{2}(t_{1}-t_{k-1})+\beta_{3}(t_{2}-t_{k-1})+\ldots\\
&& + \beta_{k-1}(t_{k-2}-t_{k-1})]/(t_{k-1}-t_{k})\nonumber .
\end{array}
A test of linearity in X can be obtained by testing
$$H_{0} : \beta_{2} = \beta_{3} = \ldots = \beta_{k-1} = 0.$$
Example: @sel10gly
<img src="images/sel10gly.png" width="100%">
### Choosing Number and Position of Knots {#sec-knots}
`r mrg(sound("genreg-6"))`
* Knots are specified in advance in regression splines `r ipacue()`
* Locations not important in most situations---
@sto86com, @dur89fle
* Place knots where
data exist --- fixed quantiles of predictor's marginal distribution
* Fit depends more on choice of $k$
```{r echo=FALSE}
require(kableExtra)
w <- data.frame(
k=3:7,
skip=' ',
a=c( '', '', '', '.05', '.025'),
b=c( '', '', '.05', '.23', '.1833'),
c=c('.10', '.05','.275','.41','.3417'),
d=c( '.5', '.35', '.5','.59', '.5'),
e=c('.90', '.65','.725','.77','.6583'),
f=c( '', '.95', '.95','.95','.8167'),
g=c( '', '', '', '', '.975'))
kable(w, booktabs=TRUE, col.names=NULL) %>%
add_header_above(c('k'=1, ' '=1, 'Quantiles'=7)) %>%
kable_paper(full_width=FALSE)
```
<!--
| k | \multicolumn{7}{|c}{Quantiles} |
|-----|-----|
| 3 ||| .10 | .5 | .90 || |
| 4 | | | .05 | .35 | .65 | .95 | |
| 5 | | .05 | .275 | .5 | .725 | .95 | |
| 6 | .05 | .23 | .41 | .59 | .77 | .95 | |
| 7 | .025 | .1833 | .3417 | .5 | .6583 | .8167 | .975 |
-->
$n<100$ -- replace outer quantiles with 5th smallest and 5th largest $X$
(@sto85add).
Choice of $k$:
* Flexibility of fit vs. $n$ and variance `r ipacue()`
* Usually $k=3,4,5$. Often $k=4$
* Large $n$ (e.g. $n\geq 100$) -- $k=5$
* Small $n$ ($<30$, say) -- $k=3$
* Can use Akaike's information criterion (AIC) (@atk80not, @hou90pre) to choose $k$
* This chooses $k$ to maximize model likelihood ratio $\chi^{2} - 2k$.
See @gov07com for a comparison of restricted cubic splines,
fractional polynomials, and penalized splines.
### Nonparametric Regression {#sec-nonpar.reg}
`r mrg(sound("genreg-7"))`
* Estimate tendency (mean or median) of $Y$ as a function of $X$ `r ipacue()`
* Few assumptions
* Especially handy when there is a single $X$
* Plotted trend line may be the final result of the analysis
* Simplest smoother: moving average <br>
| $X$: | 1 | 2 | 3 | 5 | 8 |
|-----|-----|-----|-----|-----|-----|
| $Y$: | 2.1 | 3.8 | 5.7 | 11.1 | 17.2 |
\begin{array}{ccc}
\hat{E}(Y | X=2) &=& \frac{2.1+3.8+5.7}{3} \\
\hat{E}(Y | X=\frac{2+3+5}{3}) &=& \frac{3.8+5.7+11.1}{3}
\end{array}
* overlap OK
* problem in estimating $E(Y)$ at outer $X$-values
* estimates very sensitive to bin width
* Moving linear regression far superior to moving avg. (moving
flat line) `r ipacue()`
* @cle79rob moving linear regression smoother _loess_ (locally weighted least squares) is the most popular
smoother. To estimate central tendency of $Y$ at $X=x$:
+ take all the data having $X$ values within a suitable interval
about $x$ (default is $\frac{2}{3}$ of the data)
+ fit weighted least squares linear regression within this
neighborhood
+ points near $x$ given the most weight^[Weight here means something different than regression coefficient. It means how much a point is emphasized in developing the regression coefficients.]
+ points near extremes of interval receive almost no weight
+ loess works much better at extremes of $X$ than moving avg.
+ provides an estimate at each observed $X$; other estimates
obtained by linear interpolation
+ outlier rejection algorithm built-in
* loess works for binary $Y$ --- just turn off outlier detection `r ipacue()`
* Other popular smoother: Friedman's "super smoother"
* For loess or supsmu amount of smoothing can be controlled by analyst
* Another alternative: smoothing splines^[These place knots at all the observed data points but penalize coefficient estimates towards smoothness.]
* Smoothers are very useful for estimating trends in residual
plots
### Advantages of Regression Splines over Other Methods
`r mrg(sound("genreg-8"))`
Regression splines have several advantages (@har88reg):
* Parametric splines can be fitted using any existing `r ipacue()`
regression program
* Regression coefficients estimated using standard
techniques (ML or least squares), formal tests of no overall association, linearity, and additivity, confidence limits for the estimated regression
function are derived by standard theory.
* The fitted function directly estimates transformation predictor
should receive to yield linearity in $C(Y|X)$.
* Even when a simple transformation is obvious, spline function
can be used to represent the predictor in the final model (and the
d.f. will be correct). Nonparametric methods do not yield a
prediction equation.
* Extension to non-additive models. <br> Multi-dimensional
nonparametric estimators often require burdensome computations.
## Recursive Partitioning: Tree-Based Models {#sec-tree.models}
@bre84cla: CART (Classification and Regression Trees) --- essentially model-free
Method:
* Find predictor so that best possible binary split has maximum `r ipacue()`
value of some statistic for comparing 2 groups
* Within previously formed subsets, find best predictor and split
maximizing criterion in the subset
* Proceed in like fashion until $<k$ obs. remain to split
* Summarize $Y$ for the terminal node (e.g., mean, modal category)
* Prune tree backward until it cross-validates as well as its
"apparent" accuracy, or use shrinkage
Advantages/disadvantages of recursive partitioning:
* Does not require functional form for predictors `r ipacue()`
* Does not assume additivity --- can identify complex interactions
* Can deal with missing data flexibly
* Interactions detected are frequently spurious
* Does not use continuous predictors effectively
* Penalty for overfitting in 3 directions
* Often tree doesn't cross-validate optimally unless pruned
back very conservatively
* Very useful in messy situations or those in which overfitting
is not as problematic (confounder adjustment using propensity
scores @coo88asy; missing value imputation)
See @aus10log.
### New Directions in Predictive Modeling
`r mrg(sound("genreg-9"))`
The approaches recommended in this course are
* fitting fully pre-specified models without deletion of `r ipacue()`
"insignificant" predictors
* using data reduction methods (masked to $Y$) to reduce the
dimensionality of the predictors and then fitting the number of
parameters the data's information content can support
* use shrinkage (penalized estimation) to fit a large model
without worrying about the sample size.
The data reduction approach can yield very interpretable, stable
models, but there are many decisions to be made when using a two-stage
(reduction/model fitting) approach, Newer approaches are evolving,
including the following. These new approach handle continuous
predictors well, unlike recursive partitioning.
* lasso (shrinkage using L1 norm favoring zero regression `r ipacue()`
coefficients) - @tib96reg, @ste00pro
* elastic net (combination of L1 and L2 norms that handles the
$p > n$ case better than the lasso) @zou05reg
* adaptive lasso @zha07ada, @wan07uni
* more flexible lasso to differentially penalize for variable
selection and for regression coefficient estimation (@rad08var)
* group lasso to force selection of all or none of a group of
related variables (e.g., indicator variables representing a polytomous
predictor)
* group lasso-like procedures that also allow for variables within a
group to be removed (@wan09hie)
* sparse-group lasso using L1 and L2 norms to achieve spareness on
groups and within groups of variables (@sim13spa)
* adaptive group lasso (Wang \& Leng)
* Breiman's nonnegative garrote (@xio10not)
* "preconditioning", i.e., model simplification after developing
a "black box" predictive model - @pau08pre,@not10bay
* sparse principal components analysis to achieve
parsimony in data reduction @wit08tes,@zho06spa,@len09gen,@lee10spa
* bagging, boosting, and random forests @has08ele
One problem prevents most of these methods from being ready for everyday use: `r ipacue()`
they require scaling predictors before fitting the model. When a
predictor is represented by nonlinear basis functions, the scaling
recommendations in the literature are not sensible. There are also
computational issues and difficulties obtaining hypothesis tests and
confidence intervals.
When data reduction is not required, generalized additive
models @has90gen, @woo06gen should also be considered.
### Choosing Between Machine Learning and Statistical Modeling
* Statistical models allow for complexity (nonlinearity, interaction)
* Easy to allow every predictor to have nonlinear effect
* Easy to handle unlimited numbers of candidate predictors if
assume additivity (e.g., using ridge regression, lasso, elastic net)
* Interactions should be pre-specified
* Machine learning is gaining attention but is oversold in some settings
`r mrg(blog("medml"))`
* Researchers are under the mistaken impression that machine
learning can be used on small samples
`r mrg(blog("ml-sample-size"))`
* See [A brief tour of deep learning from a statistical perspective](https://www.annualreviews.org/content/journals/10.1146/annurev-statistics-032921-013738) by E Nalisnick, P Smyth, D Tran, 2023.
**Considerations in Choosing One Approach over Another**
A statistical model may be the better choice if
* Uncertainty is inherent and the signal:noise ratio is not large;
even with identical twins, one twin may
get colon cancer and the other not; model tendencies instead of
doing classification
* One could never have perfect training data, e.g., cannot
repeatedly test one subject and have outcomes assessed without error
* One wants to isolate effects of a small number of variables
* Uncertainty in an overall prediction or the effect of a
predictor is sought
* Additivity is the dominant way that predictors affect the
outcome, or interactions are relatively small in number and can be
pre-specified
* The sample size isn't huge
* One wants to isolate (with a predominantly additive effect) the
effects of "special" variables such as treatment or a risk factor
* One wants the entire model to be interpretable
Machine learning may be the better choice if
* The signal:noise ratio is large and the outcome being predicted
doesn't have a strong component of
randomness; e.g., in visual pattern recognition an object must be an "E"
or not an "E"
* The learning algorithm can be trained on an unlimited number of
exact replications (e.g., 1000 repetitions of each letter in the
alphabet or of a certain word to be translated to German)
* Overall prediction is the goal, without being able to succinctly
describe the impact of any one variable (e.g., treatment)
* One is not very interested in estimating uncertainty in
forecasts or in effects of select predictors
* Non-additivity is expected to be strong and can't be isolated to
a few pre-specified variables (e.g., in visual pattern recognition
the letter "L" must have both a dominating vertical component and
a dominating horizontal component)
* The sample size is huge (@plo14mod)
* One does not need to isolate the effect of a special variable
such as treatment
* One does not care that the model is a "black box"
But see [this](https://bsky.app/profile/gscollins.bsky.social/post/3laufggkuxc2u) for navigating resources exposing problems in ML applications such as the following:
* Weak design and methods
* Poor reporting
* High risk of bias
* Spin
* Non-open science
## Multiple Degree of Freedom Tests of Association {#sec-multiple.df}
`r mrg(sound("genreg-10"))`
`r ipacue()`
$$C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{2}^{2} ,$$
$H_{0}: \beta_{2}=\beta_{3}=0$ with 2 d.f. to assess association
between $X_{2}$ and outcome.
In the 5-knot restricted cubic spline model
$$C(Y|X) = \beta_{0}+\beta_{1}X+\beta_{2}X'+\beta_{3}X''+\beta_{4}X''' ,$$
$H_{0}: \beta_{1}=\ldots=\beta_{4}=0$
* Test of association: 4 d.f. `r ipacue()`
* Insignificant $\rightarrow$ dangerous to interpret plot
* What to do if 4 d.f. test insignificant, 3 d.f. test for
linearity insig., 1 d.f. test sig. after delete nonlinear
terms?
@gra91eff elegantly described the hazards of
pretesting
* Studied quadratic regression `r ipacue()`
* Showed 2 d.f. test of association is nearly optimal even when
regression is linear if nonlinearity **entertained**
* Considered ordinary regression model <br>
$E(Y|X) =\beta_{0}+\beta_{1}X+\beta_{2}X^{2}$
* Two ways to test association between $X$ and $Y$
* Fit quadratic model and test for linearity ($H_{0}:
\beta_{2}=0$)
* $F$-test for linearity significant at $\alpha=0.05$ level
$\rightarrow$ report as the
final test of association the 2 d.f. $F$ test of $H_{0}:
\beta_{1}=\beta_{2}=0$
* If the test of linearity insignificant, refit without the
quadratic term and final test of association is 1 d.f. test,
$H_{0}:\beta_{1}=0 | \beta_{2}=0$
* Showed that type I error $> \alpha$
* Fairly accurate $P$-value obtained by instead testing against
$F$ with 2 d.f. even at second stage
* Cause: are retaining the most significant part of $F$
* **BUT** if test against 2 d.f. can only lose power when
compared with original $F$ for testing both $\beta$s
* $SSR$ from quadratic model $> SSR$ from linear model
## Assessment of Model Fit
`r mrg(sound("genreg-11"))`
### Regression Assumptions
The general linear regression model is `r ipacue()`
$$C(Y|X) = X\beta =\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{k}X_{k} .$$
Verify linearity and additivity. Special case:
$$C(Y|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2},$$
where $X_{1}$ is binary and $X_{2}$ is continuous.
```{r regass,echo=FALSE,cap='Regression assumptions for one binary and one continuous predictor'}
#| label: fig-gen-regass
spar(axes=FALSE)
plot(0:1, 0:1, xlab=expression(X[2]), ylab=expression(C(Y)),
axes=FALSE, type='n')
axis(1, at=0:1, labels=rep('',2))
axis(2, at=0:1, labels=rep('',2))
lines(c(.05, .8), c(.05, .5))
lines(c(.05, .8), c(.30, .75))
text(.9, .5, expression(X[1]==0), adj=.5)
text(.9, .75,expression(X[1]==1), adj=.5)
```
Methods for checking fit:
**1. Fit simple linear additive model and check examine residual plots for patterns**
`r ipacue()`
* For OLS: box plots of $e$ stratified by $X_{1}$,
scatterplots of $e$ vs. $X_{2}$ and $\hat{Y}$, with trend
curves (want flat central tendency, constant variability)
* For normality, `qqnorm` plots of overall and stratified
residuals
**Advantage**: Simplicity
**Disadvantages**:
* Can only compute standard residuals for uncensored continuous
response
* Subjective judgment of non-randomness
* Hard to handle interaction
* Hard to see patterns with large $n$ (trend lines help)
* Seeing patterns does not lead to corrective action
**2. Scatterplot of $Y$ vs. $X_{2}$ using different symbols according to values of $X_{1}$**
`r ipacue()`
**Advantages**: Simplicity, can see interaction
**Disadvantages**:
* Scatterplots cannot be drawn for binary, categorical, or
censored $Y$
* Patterns difficult to see if relationships are weak or $n$
large
**3. Stratify the sample by $X_{1}$ and quantile groups (e.g. deciles) of $X_{2}$; estimate $C(Y|X_{1},X_{2})$ for each stratum**
**Advantages**: Simplicity, can see interactions, handles censored $Y$ (if you are careful)
**Disadvantages**:
* Requires large $n$
* Does not use continuous var. effectively (no interpolation)
* Subgroup estimates have low precision
* Dependent on binning method
**4. Separately for levels of $X_{1}$ fit a nonparametric smoother relating $X_{2}$ to $Y$**
`r ipacue()`
**Advantages**: All regression aspects of the model can be summarized efficiently with minimal assumptions
**Disadvantages**:
* Does not apply to censored $Y$
* Hard to deal with multiple predictors
**5. Fit flexible nonlinear parametric model**
**Advantages**:
* One framework for examining the model assumptions, fitting the
model, drawing formal inference
* d.f. defined and all aspects of statistical
inference "work as advertised"
**Disadvantages**:
* Complexity
* Generally difficult to allow for interactions when assessing
patterns of effects
Confidence limits, formal inference can be problematic for methods 1-4. `r ipacue()`
Restricted cubic spline works well for method 5.
\begin{array}{ccc}
\hat{C}(Y|X) &=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+\hat{\beta}_{2}X_{2}+\hat{\beta}_{3}X_{2}'+\hat{\beta}_{4}X_{2}'' \nonumber\\
&=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+\hat{f}(X_{2}) ,
\end{array}
where
$$\hat{f}(X_{2}) = \hat{\beta}_{2}X_{2}+\hat{\beta}_{3}X_{2}'+\hat{\beta}_{4}X_{2}'' ,$$
$\hat{f}(X_{2})$ spline-estimated transformation of $X_{2}$.
* Plot $\hat{f}(X_{2})$ vs. $X_{2}$ `r ipacue()`
* $n$ large $\rightarrow$ can fit separate functions by $X_{1}$
* Test of linearity: $H_{0}:\beta_{3}=\beta_{4}=0$
* Few good reasons to do the test other than to demonstrate that
linearity is not a good default assumption
* Nonlinear $\rightarrow$ use transformation suggested by spline fit
or keep spline terms
* Tentative transformation $g(X_{2})$ $\rightarrow$ check adequacy
by expanding $g(X_{2})$ in spline function and testing linearity
* Can find transformations by plotting $g(X_{2})$ vs. $\hat{f}(X_{2})$ for
variety of $g$
* Multiple continuous predictors $\rightarrow$ expand each using spline
* Example: assess linearity of $X_{2}, X_{3}$
`r ipacue()`
\begin{array}{ccc}
C(Y|X) &=& \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{2}'+\beta_{4}X_{2}'' \nonumber\\
&+& \beta_{5}X_{3}+\beta_{6}X_{3}'+\beta_{7}X_{3}'' ,
\end{array}
Overall test of linearity $H_{0}: \beta_{3}=\beta_{4}=\beta_{6}=\beta_{7}=0$, with 4 d.f.
### Modeling and Testing Complex Interactions {#sec-interaction.surface}
`r mrg(sound("genreg-12"))`
**Note**: Interactions will be misleading if main effects are not properly modeled (@zha20int).
Suppose $X_1$ binary or linear, $X_2$ continuous:
`r ipacue()`
\begin{array}{ccc}
C(Y|X) & = & \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{2}'+\beta_{4}X_{2}'' \\ \nonumber
&&+\beta_{5}X_{1}X_{2}+\beta_{6}X_{1}X_{2}'+\beta_{7}X_{1}X_{2}''
\end{array}
Simultaneous test of linearity and additivity:
$H_{0}: \beta_{3} = \ldots = \beta_{7} = 0$.
* 2 continuous variables: could transform separately and form `r ipacue()`
simple product
* **But** transformations depend on whether interaction terms
adjusted for, so it is usually not possible to estimate
transformations and interaction effects other than simultaneously
* Compromise: Fit interactions of the form $X_{1} f(X_{2})$ and
$X_{2} g(X_{1})$:
`r ipacue()`
$$\begin{array}{ccc}
C(Y|X) & = & \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{1}'+\beta_{3}X_{1}'' \nonumber\\
&+& \beta_{4}X_{2}+\beta_{5}X_{2}'+\beta_{6}X_{2}'' \nonumber\\
&+& \beta_{7}X_{1}X_{2}+\beta_{8}X_{1}X_{2}'+\beta_{9}X_{1}X_{2}'' \\
&+& \beta_{10}X_{2}X_{1}'+\beta_{11}X_{2}X_{1}'' \nonumber
\end{array}$$ {#eq-restricted-ia}
* Test of additivity is $H_{0}: \beta_{7} = \beta_{8} = \ldots = \beta_{11} = 0$ with 5 d.f. `r ipacue()`
* Test of lack of fit for the simple product interaction with
$X_{2}$ is $H_{0}: \beta_{8} = \beta_{9} = 0$
* Test of lack of fit for the simple product interaction with
$X_{1}$ is $H_{0}: \beta_{10} = \beta_{11} = 0$
General spline surface:
* Cover $X_{1} \times X_{2}$ plane with grid and `r ipacue()`
fit patch-wise cubic polynomial in two variables
* Restrict to be of form $aX_{1}+bX_{2}+cX_{1}X_{2}$ in corners
* Uses all $(k-1)^{2}$ cross-products of restricted cubic
spline terms
* See @gra92fle, @gra94spl for penalized splines
allowing control of effective degrees of freedom. See
@ber08usi for a good discussion of tensor splines.
```{r echo=FALSE}
#| label: fig-gen-image-stroke
#| fig-cap: "Logistic regression estimate of probability of a hemorrhagic stroke for patients in the GUSTO-I trial given $t$-PA, using a tensor spline of two restricted cubic splines and penalization (shrinkage). Dark (cold color) regions are low risk, and bright (hot) regions are higher risk."
#| fig-scap: "Probability of hemorrhagic stroke vs. blood pressures"
knitr::include_graphics('images/image-stroke.png')
```
@fig-gen-image-stroke is particularly interesting
because the literature had suggested (based on approximately 24
strokes) that pulse pressure was the main
cause of hemorrhagic stroke whereas this flexible modeling approach
(based on approximately 230 strokes)
suggests that mean arterial blood pressure (roughly a $45^\circ$ line)
is what is most important
over a broad range of blood pressures. At the far right one can see
that pulse pressure (axis perpendicular to $45^\circ$ line) may have
an impact although a non-monotonic one.
Other issues:
* $Y$ non-censored (especially continuous) $\rightarrow$ multi-dimensional `r ipacue()`
scatterplot smoother (@Swhite)
* Interactions of order $>2$: more trouble
* 2-way interactions among $p$ predictors: pooled tests
* $p$ tests each with $p-1$ d.f.
Some types of interactions to pre-specify in clinical studies:
* Treatment $\times$ severity of disease being treated `r ipacue()`
* Age $\times$ risk factors
* Age $\times$ type of disease
* Measurement $\times$ state of a subject during measurement
* Race $\times$ disease
* Calendar time $\times$ treatment
* Quality $\times$ quantity of a symptom
* Measurement $\times$ amount of deterioration of the measurement
<!-- \nosound -->
The last example is worth expanding as an example in model formulation. Consider the following study.
* A sample of patients seen over several years have a blood sample taken at time of hospitalization `r ipacue()`
* Blood samples are frozen
* Long after the last patient was sampled, the blood samples are thawed all in the same week and a blood analysis is done
* It is known that the quality of the blood analysis deteriorates roughly logarithmically by the age of the sample; blood measurements made on old samples are assumed to be less predictive of outcome
* This is reflected in an interaction between a function of sample age and the blood measurement `B`^[For continuous $Y$ one might need to model the residual variance of $Y$ as increasing with sample age, in addition to modeling the mean function.]
* Patients were followed for an event, and the outcome variable of interest is the time from hospitalization to that event
* To not assume a perfect logarithmic relationship for sample age on the effect of the blood measurement, a restricted cubic spline model with 3 default knots will be fitted for log sample age
* Sample age is assumed to not modify the effects of non-blood predictors patient `age` and `sex`
* Model may be specified the following way using the `R` `rms` package to fit a Cox proportional hazards model
* Test for nonlinearity of `sampleAge` tests the adequacy of assuming a plain logarithmic trend in sample age
```{r detmodel,eval=FALSE}
f <- cph(Surv(etime, event) ~ rcs(log(sampleAge), 3) * rcs(B, 4) +
rcs(age, 5) * sex, data=mydata)
```
The `B` $\times$ `sampleAge` interaction effects have 6 d.f. and tests whether the sample deterioration affects the effect of `B`. By not assuming that `B` has the same effect for old samples as for young samples, the investigator will be able to estimate the effect of `B` on outcome when the blood analysis is ideal by inserting `sampleAge` = 1 day when requesting predicted values as a function of `B`.
<!-- \enosound -->
### Fitting Ordinal Predictors
* Small no. categories (3-4) $\rightarrow$ polytomous factor, indicator variables `r ipacue()`
* Design matrix for easy test of adequacy of initial codes $\rightarrow$
$k$ original codes + $k-2$ indicators
* More categories $\rightarrow$ score using data-driven trend. Later
tests use $k-1$ d.f. instead of 1 d.f.
* E.g., compute logit(mortality) vs. category
* Much better: used penalized maximum likelihood estimation (`R`
`ordSmooth` package) or Bayesian shrinkage (`R` `brms` package).
### Distributional Assumptions
* Some models (e.g., logistic): all assumptions in $C(Y|X)=X\beta$ `r ipacue()`
(implicitly assuming no omitted variables!)
* Parametric models make an absolute distributional assumption
+ E.g. linear regression: $Y \sim X\beta + \epsilon, \epsilon \sim n(0,\sigma^{2})$
+ Examine distribution of residuals
* Some models (Weibull, @cox72reg): <br>
$C(Y|X) = C(Y=y|X) = d(y) + X\beta$ <br>
$C =$ log hazard
* Check form of $d(y)$ for parametric models such as Weibull
* For semiparametric models (Cox and ordinal regression) $d(y)$ does not need to be specified
+ $d(y)$ is estimated by a step function (is link function of empirical CDF when $\beta=0$)
* Show $d(y)$ does not interact with $X$ (parallelism assumption)
## Complex Curve Fitting Example {#sec-genreg-gtrans}
* Restricted cubic spline `r ipacue()`
* Discontinuity (interrupted time series analysis)
* Cyclic trend (seasonality)
* Data from [academic.oup.com/ije/article/46/1/348/2622842](https://academic.oup.com/ije/article/46/1/348/2622842) by @ber17int
* Rates of hospital admissions for acute coronary events in Sicily before and after a smoking ban on 2005-01
* Poisson regression on case counts, adjusted for population size
as an offset variable (analyzes event rate) (see [stats.stackexchange.com/questions/11182](https://stats.stackexchange.com/questions/11182))
* Classic interrupted time series puts a discontinuity at the intervention point and assesses statistical evidence for a nonzero jump height
* We will do that and also fit a continuous cubic spline but with multiple knots near the intervention point
* All in context of long-term and seasonal trends
* Uses the `rms` package `gTrans` function documented at [hbiostat.org/R/rms/gtrans.html](https://hbiostat.org/R/rms/gtrans.html)
* Can do this without `gTrans` but harder to plot predicted values, get contrasts, and get chunk tests
* Time variable is months after 2001-12-01
```{r sicily}
require(rms) # engages rms which also engages Hmisc which provides getHdata
options(prType='html') # applies to printing model fits
getHdata(sicily) # fetch dataset from hbiostat.org/data
d <- sicily
dd <- datadist(d); options(datadist='dd')
```
Start with a standard restricted cubic spline fit, 6 knots at default quantile locations. From the fitted Poisson model we estimate the number of cases per a constant population size of 100,000.
```{r sic}
require(ggplot2)
g <- function(x) exp(x) * 100000
off <- list(stdpop=mean(d$stdpop)) # offset for prediction (383464.4)
w <- geom_point(aes(x=time, y=rate), data=d)
v <- geom_vline(aes(xintercept=37, col=I('red')))
yl <- ylab('Acute Coronary Cases Per 100,000')
f <- Glm(aces ~ offset(log(stdpop)) + rcs(time, 6),
data=d, family='poisson')
f$aic
ggplot(Predict(f, fun=g, offset=off)) + w + v + yl
```
* To add seasonality to the model can add sine and/or cosine terms `r ipacue()`
* See [pmean.com/07/CyclicalTrends.html](http://www.pmean.com/07/CyclicalTrends.html) by Steve Simon
* If you knew the month at which incidence is a minimum, could just add a sine term to the model
* Adding both sine and cosine terms effectively allows for a model parameter that estimates the time origin
* Assume the period (cycle length) is 12m
```{r sic2}
# Save knot locations
k <- attr(rcs(d$time, 6), 'parms')
k
kn <- k
# rcspline.eval is the rcs workhorse
h <- function(x) cbind(rcspline.eval(x, kn),
sin=sin(2*pi*x/12), cos=cos(2*pi*x/12))
f <- Glm(aces ~ offset(log(stdpop)) + gTrans(time, h),
data=d, family='poisson')
f$aic
ggplot(Predict(f, fun=g, offset=off)) + w + v + yl
```
Next add more knots near intervention to allow for sudden change
```{r sic3}
kn <- sort(c(k, c(36, 37, 38)))
f <- Glm(aces ~ offset(log(stdpop)) + gTrans(time, h),
data=d, family='poisson')
f$aic
ggplot(Predict(f, fun=g, offset=off)) + w + v + yl
```
Now make the slow trend simpler (6 knots) but add a discontinuity at the intervention. More finely control times at which predictions are requested, to handle discontinuity.
```{r sic4}
h <- function(x) {
z <- cbind(rcspline.eval(x, k),
sin=sin(2*pi*x/12), cos=cos(2*pi*x/12),
jump=x >= 37)
attr(z, 'nonlinear') <- 2 : ncol(z)
z
}
f <- Glm(aces ~ offset(log(stdpop)) + gTrans(time, h),
data=d, family='poisson', x=TRUE, y=TRUE) # x, y for LRTs
f$aic
times <- sort(c(seq(0, 60, length=200), 36.999, 37, 37.001))
ggplot(Predict(f, time=times, fun=g, offset=off)) + w + v + yl
```
Look at fit statistics especially evidence for the jump
<small>
```{r sic5}
f
```
</small>
* Evidence for an intervention effect (jump) `r ipacue()`
* Evidence for seasonality
* Could have analyzed rates using a semiparametric model
Compute likelihood ratio $\chi^2$ test statistics for this model
```{r}
anova(f, test='LR')
```
Get a joint LR test of seasonality and discontinuity by omitting 3 terms from the model
```{r}
g <- Glm(aces ~ offset(log(stdpop)) + rcs(time, k),
data=d, family='poisson')
lrtest(f, g)
```
<!-- NEW -->
## Contrasts and Model Reparameterization {#sec-genreg-repar}
Contrasts allow one to estimate and test any kind of effects that are napped to the model's regression parameters. Examples in @sec-genreg-prior show how far you can take this idea, including double difference contrasts for estimating interaction effects or degree of nonlinearity. The `rms` package `contrast.rms` function makes it easy to estimate contrasts to get estimates such as the effect of age changing from 30 to 50 for males. Contrasts are just differences in predicted values, so all that's needed is to specify the design matrices for one condition vs. another and to subtract these two matrices and multiply this difference by $\hat{\beta}$. A standard formula is used to compute standard errors of such contrasts which leads to Wald confidence intervals.
Since Wald confidence intervals for contrasts are so easy to compute, it is tempting to always compute contrasts in an after-fitting step. This is optimal for bootstrapping, or for Bayesian models where the contrast is computed separately for each posterior draw, leading to posterior samples of the contrasts, which are summarized exactly as basic parameters are summarized (posterior median, highest posterior density uncertainty interval, etc.). But in a frequentist setting outside of a standard Gaussian linear model, Wald confidence intervals are not ideal. For example the sampling distribution of the contrast may be asymmetric, so symmetric confidence intervals may have poor coverage on at least one side. In addition, Wald confidence intervals may inconsistent with gold-standard likelihood ratio $\chi^2$ tests, whereas profile likelihood confidence intervals are consistent with them.
To compute profile likelihood confidence intervals on a contrast, one must reparameterize the model with $p$ parameters so that the contrast is represented by a single variable, with the model's $p-1$ parameters reparameterized so that the contrast and the $p-1$ parameters span the same space as the original model. This allows profile likelihood algorithms to fix the contrast "parameter" at a given constant $c$, compute maximum likelihood estimates of the remaining new parameters, and repeat this process many times to solve for the two values of $c$ such that the interval between them is the set of values that if hyothesized to be true would not lead to rejection of the null using the likelihood ratio $\chi^2$ test.
How does one derive the "contrast variable" and the remaining $p-1$ variables? How can the contrast variable be constructed so that its estimated regression coefficient is exactly equal to the estimated contrast? This is a useful exercise in understanding regression model algebra even if not using profile likelihoods.
Consider a very simple case where the model is $E(Y | X=x) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} = f(x_1, x_2)$, where the vector $x$ is $[x_1, x_2]$. Suppose the contrast of interest is just $\beta_1$, i.e., the contrast is $f(1, a) - f(0, a)$. The setting for $x_2$, $a$, is irrelevant and will cancel out since $x_1$ and $x_2$ do not interact. Se we are not reparameterizing the model; the matrix multiplication that translates from the original $x$ space to the new space involves a $2\times 2$ identity matrix, and one fits the model with the original $x$ values to get the contrast of interest as the $\hat{\beta_1}$.
Next consider a more meaningful case there the contrast of interest is $\beta_1 - \beta_2$. Intuition tells us that the rephrasing of parameters needed for the model's second variable is $\beta_1 + \beta_2$ which is orthogonal to the first combination. Let's use a general procedure to derive this second parameter. If we augment the first new parameter with the identity matrix that represents the original model, a singular value decomposition will yield the second variable that will make the modified model span the same space as the original. The R code below demonstrates this.
```{r}
p <- 2 # number of non-intercept parameters
D <- c(1, -1) # contrast of interest
C <- rbind(D, diag(p)) # diag(p) is 2x2 identity matrix
C
s <- svd(C)
s
v <- s$v[, 2 : p, drop=FALSE]
v
```
The coefficients of $x_1$ and $x_2$ in `v` are the same, so the second parameter is associated with the sum of $x_1$ and $x_2$, with an arbitrary scaling constant.
Now consider a more interested case. A model has a predictor $x$ that is modeled with an ordinary cubic polynomial plus a discontinuity at $x=3$ and includes another covariate $z$:
$$
\begin{aligned}
E(Y | x, z) = f(x, z) &= \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 \\
&+ \beta_4 [x > 3] + \beta_5 z
\end{aligned}
$$
Here $[s]$ is a 0/1 indicator variable for the truth of assertion $s$. Our contrast of interest is $f(3, a) - f(1, a)$ which is $2\beta_1 + 8\beta_2 + 26\beta_3$. $a$ cancels out and $\beta_4$ is not involved either since $x \leq 3$ for both contrast predictor settings. We need to create a new variable $u$ that, when adjusted for the correct parameterization of the other variables, will result in a regression coefficient that is exactly $2\beta_1 + 8\beta_2 + 26\beta_3$ in the original $\beta$s. Try $u = (\frac{x}{2} + \frac{x^2}{8} + \frac{x^3}{26}) / 3$. Simulate some data and use the singular value decomposition to solve for the matrix to multiply the design matrix by to reparameterize the other parts of the model. Below `xc` (`x` contrast variable) is $u$.
```{r}
set.seed(1)
n <- 100; b0=3; b1=1; b2=.2; b3=.05; b4=1; b5=2
x <- 2 * rnorm(n)
z <- rnorm(n)
res <- 2 * rnorm(n)
d <- data.frame(x, z)
dd <- datadist(d); options(datadist='dd')
y <- b0 + b1*x + b2*x^2 + b3*x^3 + b4*(x > 3) + b5*z + res
# Form a general transformation function fo x
g <- function(x) cbind(x=x, x2=x^2, x3=x^3, x4=x > 3)
f <- orm(y ~ gTrans(x, g) + z, x=TRUE, y=TRUE)
f
# For the contrast matrix setting z arbitrarily to pi
X1 <- predict(f, data.frame(x=1, z=pi), type='x')
X2 <- predict(f, data.frame(x=3, z=pi), type='x')
rbind(X1, X2)
D <- X2 - X1
D
D %*% coef(f)[- (1 : num.intercepts(f))]
p <- ncol(D)
C <- rbind(D, diag(p)); C
s <- svd(C); s
# Need to account for a scaling constant used in SVD
v <- s$v * sqrt(sum(D ^ 2))
v
v <- s$v / sqrt(sum(D ^ 2)) # do the reverse when solving for x
v
# Get original design matrix and rotate it
# Contrast of interest is in the 1st column, all other columns
# are orthogonal to that
X <- f$x
Z <- X %*% v
orm(y ~ Z)
```
<!--
# Put single d.f. contrast in first column
# For each nonzero element of D add the original X column divided by that D element
xc <- rep(0, n)
for(i in 1 : length(D))
if(D[i] != 0) xc <- xc + X[, i] / D[i]
# Divide by number of non-zero D's so that when adding all these xc components we get 0-1 scale for
# contrast of interest
xc <- xc / sum(D != 0)
other <- X %*% v
g <- ols(y ~ xc + other)
g
-->
Compute the contrast on the original variables and compare to the coefficient of `xc`.
```{r}
k <- contrast(f, list(x=3), list(x=1))
k
p <- Predict(f, x=c(1,3))
diff(p$yhat)
```
Repeat using the more accurate profile likelihood method, which makes use of the singular value decomposition like the one above.
```{r}
contrast(f, list(x=3), list(x=1), conf.type='profile')
```
Note that singular value decompositions have arbitrary signs. The `contrast` function does any needed sign reversal so that the contrast matches the original one.
## Bayesian Modeling {#sec-genreg-bayes}
There are many advantages to fitting models with a Bayesian approach when compared to the frequentist / maximum likelihood approach that receives more coverage in this text. These advantages include
* the ability to use outside information, e.g. the direction or magnitude of an effect, magnitude of interaction effect, degree of nonlinearity
* getting exact inference (to within simulation error) regarding model parameters without using any Gaussian approximations as used so heavily in frequentist inference[Bayesian approaches do not tempt analysts to [mistakenly assume that the central limit theorem protects them](https://hbiostat.org/bbr/htest.html?q=CLT#central-limit-theorem).]{.aside}
* getting exact inference about derived parameters that are nonlinear transformations of the original model parameters, without using the $\delta$-method approximation so often required in frequentist procedures[The $\delta$-method fails when the sampling distribution of the parameter is not symmetric.]{.aside}
* devoting less than one degree of freedom to a parameter by borrowing information
* getting exact inference using ordinary Bayesian procedures when penalization/shrinkage/regularization is used to limit overfitting
* allowing one to fit [distributional models](http://paul-buerkner.github.io/brms/articles/brms_distreg.html), e.g., using a regression model for the log standard deviation in addition to one for the mean, and getting exact inference for the joint models
* obtaining automatic inference about any interval of possible parameter values instead of just using $p$-values to bring evidence against a null value[It is just as easy to compute the Bayesian probability that an odds ratio exceeds 2.0 as it is to calculate the probability that the odds ratio exceeds 1.0.]{.aside}
* obtaining exact inference about unions and intersections of various assertions about parameters, e.g., the probability that a treatment reduces mortality by any amount or reduces blood pressure by $\geq5$ mmHg
* getting exact uncertainty intervals for complex derived parameters such as the $c$-index or Somers' $D_{xy}$ that quantify the model's predictive discrimination
::: {.callout-note collapse="true"}
### Uncertainies in Model Performance Metrics
As seen in example output form the `blrm` function below, one can automatically obtain highest posterior density uncertainty intervals for any parameter including overall model performance metrics. These are derived from the $m$ posterior draws of the model's parameters by computing the model performance metric for each draw. The uncertainties captured by this process relate to the ability to well-estimate model parameters, which relates also to within-training-sample model fit. So the uncertainties reflect a similar phenomenon to what $R^{2}_\text{adj}$ measures. [Adjusted $R^2$](https://hbiostat.org/bib/r2) other than McFadden's penalize for $p$, the number of regression parameters estimated, other than the intercept. This is very similar to considering likelihood ratio $\chi^2$ statistics minus the number of degrees of freedom involved in the LR test. On the other hand, AIC approximates out-of-sample model performance by using a penalty of twice the degrees of freedom (like the seldom-used McFadden $R^{2}_\text{adj}$)
So uncertainties computed by the `blrm` function come solely from the spread of the posterior distributions, i.e., the inability of the analysis to precisely estimate the unknown parameters. They condition on the observed design matrix $X$ and do not consider other samples as would be done with out-of-sample predictive accuracy assessment with AIC, the bootstrap, or cross-validation.
When $p=1$ a rank measure of predictive discrimination such as $D_{xy}$ will have no uncertainty unless the sign of the one regression coefficient often flips over posterior draws.
:::
A major part of the arsenal of Bayesian modeling weapons is [`Stan`](https://mc-stan.org) based at Columbia University. Very general R statistical modeling packages such as `brms` and `rstanarm` are based on `Stan`.
RMS has several fully worked-out Bayesian modeling case studies. The purpose of the remainder of this chapter is to show the power of Bayes in general regression modeling.
### A General Model Specification Approach
With a Bayesian approach one can include a parameter for each aspect of the model you know exists but are unsure about. This leads to results that are not overly optimistic, because uncertainty intervals will be a little wider to acknowledge what you don't know. A good example is the [Bayesian $t$-test](https://hbiostat.org/bbr/htest#bayesian-t-test), which has a parameter for the amount of non-normality and a parameter for how unequal the variances may be in the two groups being compared. Prior distributions can favor normality and equal variance, and modeling becomes more flexible as $n \uparrow$.
Other examples of borrowing information and adding flexibility:
* include a parameter for time-varying treatment effect to not assume proportional hazards
* include a parameter for a $Y$-varying effect to not assume proportional odds
* include an interaction effect for a treatment $\times$ sex interaction and use a prior that favors the treatment effect for females being simlar to the treatment effect for males but that allows the effects to become arbitrarily different as $n \uparrow$.
Interactions bring special problems to estimation and inference. In the best of cases, an interaction requires $4 \times$ larger sample size to estimate and may require $16 \times$ the sample size to achieve the same power as a main effect test. We need a way to borrow information, essentially having an interaction term "half in" and "half out" of the model. This has been elegantly described by @sim97bay who show how to put priors on interaction terms. Using a Bayesian approach to have an interaction "half in" the model is a much more rational approach than prevailing approaches that
* use a sample that was sized for estimating main effects and not interaction effects
* use a (low power) test for interaction to decide how to analyze the treatment effect, and ignore such pre-testing when doing a statistical test (that will not preserve $\alpha$) or computing a confidence interval (that will not have the nominal $1 - \alpha$ coverage)
* use the pre-specified model with interaction, resulting in low precision because of having no way to borrow information across levels of the interacting factor
### Help in Specifying Priors {#sec-genreg-prior}
To gain the advantages of Bayesian modeling described above, doing away with binary decisions and allowing the use of outside information, one must specify prior distributions for parameters.
It is often difficult to do this, especially when there are nonlinear effects (e.g., splines) and interactions in the model. We need a way to specify priors on the original $X$ and $Y$ scales. Fortunately `Stan` provides an elegant solution.
As discussed [here](https://discourse.mc-stan.org/t/putting-priors-on-transformed-parameters) `Stan` allows one to specify priors on transformations of model parameters, and these priors propagate back to the original parameters. It is easier to specify a prior for the effect of increasing age from 30 to 60 that it is to specify a prior for the age slope. It may be difficult to specify a prior for an age $\times$ treatment interaction (especially when the age effect is nonlinear), but much easier to specify a prior for how different the treatment effect is for a 30 year old and a 60 year old. By specifying priors on one or more contrasts one can easily encode outside information / information borrowing / shrinkage.
The `rms` [`contrast` function](https://www.rdocumentation.org/packages/rms/versions/6.7-0/topics/contrast.rms) provides a general way to implement contrasts up to double differences, and more details about computations are provided in that link. The approach used for specifying priors for contrast in `rmsb::blrm` uses the same process but is even more general. Both `contrast` and `blrm` compute design matrices at user-specified predictor settings, and the contrast matrices (matrices multipled by $\hat{\beta}$) are simply differences in such design matrices. Thinking of contrasts as differences in predicted values frees the user from having to care about how parameters map to estimands, and allows an R `predict(fit, type='x')` function do the hard work. Examples of types of differences are below. [`rmsb` implements priors on contrasts starting with version 1.0-0.]{.aside}
* no difference: compute an absolute predicted value (not implemented in `blrm` for priors)
* single difference
+ treatment main effect
+ continuous predictor effects computed by subtracting predictions at two values of the predictor
* double difference
+ amount of nonlinearity (differences in slopes over intervals of the predictor)
+ interaction effect (e.g., age slope for females minus age slope for males)
* triple difference
+ amount of nonlinearity in an interaction effect
For predictors modeled linearly, the slope is the regression coefficient. For nonlinear effects where $x$ is transformed by $f(x)$, the slope at $x=\frac{a+b}{2}$ is proportionally approximated by $f(b) - f(a)$, and the slope at $x=\frac{b+c}{2}$ by $f(c) - f(b)$. The amount of nonlinearity is reflected by the difference in the two slopes, or $f(c) - f(b) -[f(b) - f(a)] = f(a) + f(c) - 2f(b)$. [This is a numerical approximation to the second derivative (slope of the slope; acceleration). It would be easy to use more accurate Lagrange interpolation derivative approximators here.]{.aside} You'll see this form specified in the `contrast` part of the `pcontrast` argument to `blrm` below.
### Examples of Priors on Contrasts {#sec-genreg-pcontrast}
Semiparametic models are introduced in @sec-ordinal but we will use one of the models---the proportional odds (PO) ordinal logistic model---in showcasing the utility of specifying priors on contrasts in order to use external information or to place restrictions on model fits. The `blrm` function in the [`rmsb` package](https://hbiostat.org/R/rmsb) implements this semiparametric model using `Stan`. Because it does not depend on knowing how to transform $Y$, I almost always use the more robust ordinal models instead of linear models. The linear predictor $X\beta$ is on the logit (log odds) scale for the PO model. This unitless scale typically ranges from -5 to 5, corresponding to a range of probabilities of 0.007 to 0.993. Default plotting uses the intercept corresponding to the marginal median of $Y$, so the log odds of the probability that $Y$ exceeds or equals this level, given $X$, is plotted. Estimates can be converted to means, quantiles, or exceedance probabilities using the `Mean`, `Quantile`, and `ExProb` functions in the `rms` and `rmsb` packages. [Ordinal models in the cumulative probability class such as the PO model have $k$ intercepts for $k+1$ distinct values of $Y$. These intercepts encode the entire empirical distribution of $Y$ for one covariate setting, hence the term _semiparametric_ and freedom from having to choose a $Y$ distribution.]{.aside}
Effects for the PO model are usually expressed as odds ratios (OR). For the case where the prior median for the OR is 1.0 (prior mean or median log(OR)=0.0) it is useful to solve for the prior SD $\sigma$ so that $\Pr(\text{OR} > r) = a = \Pr(\text{OR} < \frac{1}{r})$, leading to $a = \frac{|\log(r)|}{\Phi^{-1}(1-a)}$, computed by the `psigma` function below. Another function `.` is defined as an abbreviation for `list()` for later usage.
```{r}
psigma <- function(r, a, inline=FALSE, pr=! inline) {
sigma <- abs(log(r)) / qnorm(1 - a)
dir <- if(r > 1.) '>' else '<'
x <- if(inline) paste0('$\\Pr(\\text{OR}', dir, r, ') =', a,
' \\Rightarrow \\sigma=', round(sigma, 3), '$')
else paste0('Pr(OR ', dir, ' ', r, ') = ', a, ' ⇒ σ=', round(sigma, 3))
if(inline) return(x)
if(pr) {
cat('\n', x, '\n\n', sep='')
return(invisible(sigma))
}
sigma
}
. <- function(...) list(...)
```
Start with a simple hypothetical example:
* model has a quadratic effect of age
* age interacts with treatment
* sex is also in the model, not interacting with anything
We wish to specify a prior on the treatment effect at age 50 so that there is only a 0.05 chance that the $\text{OR} < 0.5$. `r psigma(0.5, 0.05, inline=TRUE)`. The covariate settings specified in `pcontrast` below do not mention sex, so predictions are evaluated at the default sex (the mode). Since sex does not interact with anything, the treatment difference of interest makes the sex setting irrelevant anyway.
```{r eval=FALSE}
require(rmsb)
f <- blrm(y ~ treatment * pol(age, 2) + sex,
pcontrast=list(sd=psigma(0.5, 0.05),
c1=.(treatment='B', age=50), # .() = list()
c2=.(treatment='A', age=50),
contrast=expression(c1 - c2) ) )
```
Note that the notation needed for `pcontrast` need not consider how age is modeled.
Consider a more complicated situation. Let's simulate data for one continuous predictor where the true model is a sine wave. The response variable is a slightly rounded version of a conditionally normal $Y$. [The rounding is done just to lower the number of intercepts from 199 to 52 to speed up the Bayesian PO model fits.]{.aside}
```{r}
require(rmsb)
require(ggplot2)
options(mc.cores=4, # See https://hbiostat.org/r/examples/blrm/blrm
rmsb.backend='cmdstan', rmsbdir='~/.rmsb',
prType='html')
cmdstanr::set_cmdstan_path(cmdstan.loc)
# cmdstan.loc is defined in ~/.Rprofile
set.seed(3)
n <- 200
x <- rnorm(n)
y <- round(sin(2*x) + rnorm(n), 1)
dd <- datadist(x, q.display=c(.005, .995)); options(datadist='dd')
f <- blrm(y ~ rcs(x, 6))
f
ggplot(Predict(f))
# Plot predicted mean instead of log odds
M <- Mean(f)
ggplot(Predict(f, fun=M),
ylab=expression(hat(E)(Y*"|"*x))) +
geom_smooth(mapping=aes(x,y)) +
labs(caption='Black line: posterior mean of predicted means from PO model\nBlue line: loess nonparametric smoother')
```
Now suppose that there is strong prior knowledge that the effect of `x` is linear when `x` is in the interval $[-1, 0]$. Let's reflect that by putting a very sharp prior to tilt the difference in slopes within that interval towards 0.0. `pcontrast=` specifies two separate contrasts to pull towards zero to more finely detect nonlinearity. [The examples that follow use atypically small prior standard deviations so that constraints will be obvious.]{.aside}
```{r}
con <- list(sd=rep(psigma(1.05, 0.01), 2),
c1=.(x=-1), c2=.(x=-.75), c3=.(x=-.5),
c4=.(x=-.25), c5=.(x=0),
contrast=expression(c1 + c3 - 2 * c2, c3 + c5 - 2 * c4))
f <- blrm(y ~ rcs(x, 6), pcontrast=con)
f
f$Contrast # Print the design matrix corresponding to the two contrasts
ggplot(Predict(f))
```
What happens if we moderately limit the acceleration (second derivative; slope of the slope) at 7 equally-spaced points?
```{r}
con <- list(sd=rep(0.5, 7),
c1=.(x=-2), c2=.(x=-1.5), c3=.(x=-1), c4=.(x=-.5), c5=.(x=0),
c6=.(x=.5), c7=.(x=1), c8=.(x=1.5), c9=.(x=2),
contrast=expression(c1 + c3 - 2 * c2,
c2 + c4 - 2 * c3,
c3 + c5 - 2 * c4,
c4 + c6 - 2 * c5,
c5 + c7 - 2 * c6,
c6 + c8 - 2 * c7,
c7 + c9 - 2 * c8) )
f <- blrm(y ~ rcs(x, 6), pcontrast=con)
f
f$Contrast # Print the design matrix corresponding to the two contrasts
ggplot(Predict(f))
```
Next simulate data with one continuous predictor `x1` and a 3-level grouping variable `x2`. Start with almost flat priors that allow arbitrary interaction patterns as long as `x1` has a smooth effect.
```{r}
set.seed(6)
n <- 90
x1 <- runif(n)
x2 <- sample(c('a', 'b', 'c'), n, TRUE)
y <- round(x1 + (x1 - 0.5) ^ 2 -0.4 * (x2 == 'b') + .5 * (x2 == 'c') + runif(n), 1)
dd <- datadist(x1, x2)
f <- orm(y ~ rcs(x1, 4) * x2)
ggplot(Predict(f, x1, x2))
f <- blrm(y ~ rcs(x1, 4) * x2)
f
ggplot(Predict(f, x1, x2))
```
Put priors specifying that groups `b` and `c` have a similar `x1`-shape (no partial interaction between `x1` and `b` vs. `c`). `contrast` below encodes parallelism with respect to `b` and `c`.
```{r}
con <- list(sd=rep(psigma(1.5, 0.05), 4),
c1=.(x1=0, x2='b'), c2=.(x1=0, x2='c'),
c3=.(x1=.25, x2='b'), c4=.(x1=.25, x2='c'),
c5=.(x1=.5, x2='b'), c6=.(x1=.5, x2='c'),
c7=.(x1=.75, x2='b'), c8=.(x1=.75, x2='c'),
c9=.(x1=1, x2='b'), c10=.(x1=1, x2='c'),
contrast=expression(c1 - c2 - (c3 - c4), # gap between b and c curves at x1=0 vs. x1=.25
c1 - c2 - (c5 - c6),
c1 - c2 - (c7 - c8),
c1 - c2 - (c9 - c10) ))
f <- blrm(y ~ rcs(x1, 4) * x2, pcontrast=con)
f
f$Contrast
ggplot(Predict(f, x1, x2))
```
## Study Questions
1. Contrast statistical models vs. machine learning in a few ways
**Section 2.1-2.2**
1. What is always linear in the linear model?
**Section 2.3**
1. Define an interaction effect in words
1. In a model with main effects and two-way interactions, which regression parameter is the most "universal" by virtue of being most independent of coding?
1. When a predictor is involved in an interaction, which test of association involving that predictor is preferred?
1. What are two ways of doing chunk (composite) tests?
1. Analysts want to use least squares multiple regression to
predict follow-up blood pressure from baseline blood pressure, age,
and sex. They want to use this model for estimation, prediction,
and inference (statistical tests and confidence limits). List all
of the assumptions they make by fitting the model $Y = \beta_{0} +
\beta_{1} \text{bp} + \beta_{2} \text{age} + \beta_{3} [\text{sex=female}]$.
1. List as many methods as you can for checking the assumptions you listed.
**Section 2.4.1**
1. Provide an example where categorizing a continuous predictor is a good idea
1. If you dichotomize a continuous predictor that has a smooth relationship with Y, how can you arbitrarily change its estimated regression coefficients?
1. What is a general term used for the statistical problem caused by categorizing continuous variables?
1. What tends to happen when data are used to find cutpoints for relationships that are in fact smooth?
1. What other inferential distortion is caused by categorization?
1. Is there an amount of noise that could be added to a continuous X that makes a categorized analysis better than a continuous one?
**Section 2.4.2**
1. What is the biggest drawback to using regular polynomials to fit smooth nonlinear relationships?
1. Why does a spline function require one to use a truncated term?
1. What advantages does a linearly tail-restricted cubic spline have?
1. Why are its constructed variables X' X'' X''' etc. so complex?
1. What do you need to do to handle a sudden curvature change when fitting a nonlinear spline?
1. Barring a sudden curvature change, why are knot locations not so important in a restricted cubic spline (rcs)?
1. What is the statistical term for the delimma that occurs when choosing the number of knots?
1. What is a Bayesian way of handling this?
1. What is the core idea behind Cleveland's loess smoother?
1. Can fitted spline functions for some of the predictors be an end in themselves?
**Section 2.5**
1. What is the worst thing about recursive partitioning?
1. What is a major tradeoff between the modeling strategy we will largely use and ML?
1. What are some determinants of the best choice between SM and ML?
**Section 2.6**
1. What is the main message of the Grambsch and O'Brien paper?
1. What notational error do many analysts make that lead them to ignore model uncertainty?
**Section 2.7.2**
1. Why is it a good idea to pre-specify interactions, and how is this done?
1. Why do we not fiddle with transformations of a predictor before considering interactions?
1. What 3-dimensional restriction does the cross-products of two restricted cubic splines force?
1. What is an efficient and likely-to-fit approach to allowing for the effect of measurement degradement?
```{r echo=FALSE}
saveCap('02')
```