3 Missing Data

3.1 Types of Missing Data

Missing completely at random (MCAR) A
Missing at random (MAR)¹
Informative missing (non-ignorable non-response; missing not at random; MNAR)

¹ “Although missing at random (MAR) is a non-testable assumption, it has been pointed out in the literature that we can get very close to MAR if we include enough variables in the imputation models” Harel & Zhou (2007).

See Carpenter & Smuk (2021), Schafer & Graham (2002), Donders et al. (2006), Harel & Zhou (2007), Allison (2001), White et al. (2011), Stef Buuren (2012) for an introduction to missing data and imputation concepts. See Hazewinkel et al. (2023) for a way to indirectly detect MNAR by comparing variances of response variables between treatments.

3.2 Prelude to Modeling

Quantify extent of missing data B
Characterize types of subjects with missing data
Find sets of variables that are missing on same subjects

3.3 Missing Values for Different Types of Response Variables

Serial data with subjects dropping out (not covered in this C course²
$Y$=time to event, follow-up curtailed: covered under survival analysis³
Missing time-dependent covariates in longitudinal data: Mamouris et al. (2023)
Often discard observations with completely missing $Y$ but sometimes wasteful⁴
Characterize missings in $Y$ before dropping obs.

² Twisk et al. (2013) found instability in using multiple imputation of longitudinal data, and advantages of using instead full likelihood models.

³ White & Royston (2009) provide a method for multiply imputing missing covariate values using censored survival time data.

⁴ $Y$ is so valuable that if one is only missing a $Y$ value, imputation is not worthwhile, and imputation of $Y$ is not advised if MCAR or MAR.

3.4 Problems With Simple Alternatives to Imputation

Deletion of records—

Badly biases parameter estimates when the probability of a D case being incomplete is related to $Y$ and not just $X$ (Little & Rubin, 2002).
Deletion because of a subset of $X$ being missing always results in inefficient estimates
Deletion of records with missing $Y$ can result in biases (Crawford et al., 1995) but is the preferred approach under MCAR⁵
von Hippel (2007) found advantages to a “use all variables to impute all variables then drop observations with missing $Y$” approach (but see Sullivan et al. (2015))
Lee & Carlin (2012) suggest that observations missing on both $Y$ and on a predictor of major interest are not helpful
Only discard obs. when
- MCAR can be justified
- Rarely missing predictor of overriding importance that can’t be imputed from other data
- Fraction of obs. with missings small and $n$ is large
No advantage of deletion except savings of analyst time
Making up missing data better than throwing away real data
See Knol et al. (2010)

⁵ Multiple imputation of $Y$ in that case does not improve the analysis and assumes the imputation model is correct.

Adding extra categories of categorical predictors—

Including missing data but adding a category `missing’ causes E serious biases (Allison, 2001; Jones, 1996; Vach & Blettner, 1998)
Problem acute when values missing because subject too sick
Difficult to interpret
Fails even under MCAR (Allison, 2001; Donders et al., 2006; Jones, 1996; Knol et al., 2010; van der Heijden et al., 2006)
May be OK if values are “missing” because of “not applicable”⁶
May be OK for pure prediction where interpretation of coefficients is of no interest and patterns of missingness will be the same in future data as in the training data

⁶ E.g. you have a measure of marital happiness, dichotomized as high or low, but your sample contains some unmarried people. OK to have a 3-category variable with values high, low, and unmarried—Paul Allison, IMPUTE list, 4Jul09.

Likewise, serious problems are caused by setting missing continuous predictors to a constant (e.g., zero) and adding an indicator variable to try to estimate the effect of missing values.

Two examples from Donders et al. (2006) using binary logistic regression, $N=500$.

Results of 1000 Simulations With $\beta_{1}=1.0$ with MAR and Two Types of Imputation F

Imputation	$\hat{\beta}_{1}$	S.E.	Coverage of
Method			0.90 C.I.
Single	0.989	0.09	0.64
Multiple	0.989	0.14	0.90

Now consider a simulation with $\beta_{1}=1, \beta_{2}=0$, $X_{2}$ correlated with $X_{1} (r=0.75)$ but redundant in predicting $Y$, use missingness indicator when $X_{1}$ is MCAR in 0.4 of 500 subjects. This is also compared with grand mean fill-in imputation.

Results of 1000 Simulations Adding a Third Predictor Indicating Missing for $X_{1}$} G

Imputation	$\hat{\beta}_{1}$	$\hat{\beta}_{2}$
Method
Indicator	0.55	0.51
Overall mean	0.55

In the incomplete observations the constant $X_{1}$ is uncorrelated with $X_{2}$.

3.5 Strategies for Developing an Imputation Model

The goal of imputation is to preserve the information and meaning of the non-missing data.

There is a full Bayesian modeling alternative to all the methods presented below. The Bayesian approach requires more effort but has several advantages (Erler et al., 2016).

Exactly how are missing values estimated?

Predictive model for each target uses any outcomes, all predictors in the final model other than the target, plus auxiliary variables not in the outcome model
Could ignore all other information — random or grand mean H fill-in
Can use external info not used in response model (e.g., zip code for income)
Need to utilize reason for non-response if possible
Use statistical model with sometimes-missing $X$ as response variable
Model to estimate the missing values should include all variables that are either I

related to the missing data mechanism;
have distributions that differ between subjects that have the target variable missing and those that have it measured;
associated with the sometimes-missing variable when it is not missing; or
included in the final response model (Barzi & Woodward, 2004; Harel & Zhou, 2007)

Ignoring imputation results in biased $\hat{V}(\hat{\beta})$
transcan function in Hmisc library: “optimal” transformations of all variables to make residuals more stable and to allow non-monotonic transformations
aregImpute function in Hmisc: good approximation to full Bayesian multiple imputation procedure using the bootstrap
transcan and aregImpute use the following for fitting imputation models: J

initialize NAs to median (mode for categoricals)
expand all categorical predictors using dummy variables
expand all continuous predictors using restricted cubic splines
optionally optimally transform the variable being predicted by expanding it with restricted cubic splines and using the first canonical variate (multivariate regression) as the optimum transformation (maximizing $R^2$)
one-dimensional scoring of categorical variables being predicted using canonical variates on dummy variables representing the categories (Fisher’s optimum scoring algorithm); when imputing categories, solve for which category yields a score that is closest to the predicted score

aregImpute and transcan work with K fit.mult.impute to make final analysis of response variable relatively easy
Predictive mean matching
Recursive partitioning with surrogate splits — handles case where a predictor of a variable needing imputation is missing itself. But there are problems (Penning et al., 2018) even with completely random missingness.
White et al. (2011) discusses an alternative method based on choosing a donor observation at random from the $q$ closest matches ($q=3$, for example)

3.5.1 Interactions

When interactions are in the outcome model, oddly enough it may L be better to treat interaction terms as “just another variable” and do unconstrained imputation of them (Kim et al., 2015)

3.6 Single Conditional Mean Imputation

Can fill-in using unconditional mean or median if number of M missings low and $X$ is unrelated to other $X$s
Otherwise, first approximation to good imputation uses other $X$s to predict a missing $X$
This is a single “best guess” conditional mean
$\hat{X}_{j} = Z \hat{\theta}, Z = X_{\bar j}$ plus possibly auxiliary variables that precede $X_{j}$ in the causal chain that are not intended to be in the outcome model.
Cannot include $Y$ in $Z$ without adding random errors to imputed values as done with multiple imputation (would steal info from $Y$)
Recursive partitioning can sometimes be helpful for nonparametrically estimating conditional means

3.7 Predictive Mean Matching

Developed by Little & Rubin (2002)
Replace missing value with observed value of subject having closest predicted value to the predicted value of the subject with the NA. Key considerations are how to

model the target when it is not NA
match donors on predicted values
avoid overuse of “good” donors to disallow excessive ties in imputed data
account for all uncertainties

No distributional assumptions; nicely handles target variables with strange distributions (Vink et al., 2014)
Predicted values need only be monotonically related to real predictive values
- PMM can result in some donor observations being used repeatedly N
- Causes lumpy distribution of imputed values
- Address by sampling from multinomial distribution, probabilities = scaled distance of all predicted values to predicted value ($y^{*}$) of observation needing imputing
- Tukey’s tricube function is a good weighting function (used in loess): $w_{i} = (1 - \min(d_{i}/s, 1)^{3})^{3}$,
  $d_{i} = |\hat{y_{i}} - y^{*}|$
  $s = 0.2\times\text{mean} |\hat{y_{i}} - y^{*}|$ is a good default scale factor
  scale so that $\sum w_{i} = 1$

3.7.1 Predictive Mean Matching With Constraints

PMM is empirical so it is relatively easy to add constraints
- Need sample size to be large enough so that there are several donor observations meeting the constraints
Implemented in Hmisc 5.1-1
For each variable to be imputed the user can specify an R expression that is a logical TRUE/FALSE condition specifying which observations qualify
Constraint can involve relationships between potential donor observations (variables prefixed by d$) and the recipient (target) observation (variables prefixed by r$) having the missing value
PMM on the qualifying donor observations
Example
- time 0 corresponds to the day a patient is admitted to the hospital
- day of discharge is missing for some patients
- every patient had at least one follow-up visit
- constrain the day of discharge to be before the day of the first follow-up visit

Code

a <- aregImpute(~ age + day_dis + day_follow_up, data=d,
                constraint=list(day_dis=expression(d$day_dis < r$day_follow_up)))

3.8 Multiple Imputation

Single imputation could use a random draw from the conditional O distribution for an individual
$\hat{X}_{j} = Z \hat{\theta} + \hat{\epsilon}, Z = [X\bar{j}, Y]$ plus auxiliary variables
$\hat{\epsilon} = n(0, \hat{\sigma})$ or a random draw from the calculated residuals
- bootstrap
- approximate Bayesian bootstrap (Harel & Zhou, 2007; Rubin & Schenker, 1991): sample with replacement from sample with replacement of residuals
Multiple imputations ($M$) with random draws
- Draw sample of $M$ residuals for each missing value to be imputed
- Average $M$ $\hat{\beta}$
- In general can provide least biased estimates of $\beta$
- Simple formula for imputation-corrected var($\hat{\beta}$)
  Function of average “apparent” variances and between-imputation variances of $\hat{\beta}$
- Even when the $\chi^2$ distribution is a good approximation when data have no missing values, the $t$ or $F$ distributions are needed to have accurate $P$-values and confidence limits when there are missings (Lipsitz et al., 2002; Reiter, 2007)
- BUT full multiple imputation needs to account for uncertainty in the imputation models by refitting these models for each of the $M$ draws
- transcan does not do that; aregImpute does
Note that multiple imputation can and should use the response variable for imputing predictors (Moons et al., 2006)
aregImpute algorithm (Moons et al., 2006) P
- Takes all aspects of uncertainty into account using the bootstrap
- Different bootstrap resamples used for each imputation by fitting a flexible additive model on a sample with replacement from the original data
- This model is used to predict all of the original missing and non-missing values for the target variable for the current imputation
- Uses flexible parametric additive regression models to impute
- There is an option to allow target variables to be optimally transformed, even non-monotonically (but this can overfit)
- By default uses predictive mean matching for imputation; no residuals required (can also do more parametric regression imputation)
- By default uses weighted PMM; many other matching options
- Uses by default van~Buuren’s “Type 1” matching to capture the right amount of uncertainty by computing predicted values for missing values using a regression fit on the bootstrap sample, and finding donor observations by matching those predictions to predictions from potential donors using the regression fit from the original sample of complete observations
- Uses Rubin’s rule to estimate variances of $\hat{\beta}$, involving between- and within-imputation variance combination
- When a predictor of the target variable is missing, it is first imputed from its last imputation when it was a target variable
- First 3 iterations of process are ignored (“burn-in”)
- Compares favorably to R MICE approach
- Example:

Code

a <- aregImpute(~ age + sex + bp + death + heart.attack.before.death,
                data=mydata, n.impute=5)
f <- fit.mult.impute(death ~ rcs(age,3) + sex +
                     rcs(bp,5), lrm, a, data=mydata)

See Barzi & Woodward (2004) for a nice review of multiple imputation with detailed comparison of results (point estimates and confidence limits for the effect of the sometimes-missing predictor) for various imputation methods. Barnes et al. (2006) have a good overview of imputation methods and a comparison of bias and confidence interval coverage for the methods when applied to longitudinal data with a small number of subjects. Horton & Kleinman (2007) have a good review of several software packages for dealing with missing data, and a comparison of them with aregImpute. Harel & Zhou (2007) provide a nice overview of multiple imputation and discuss some of the available software. White & Carlin (2010) studied bias of multiple imputation vs. complete-case analysis. White et al. (2011) provide much practical guidance.

Caution: Methods can generate imputations having very reasonable distributions but still not having the property that final response model regression coefficients have nominal confidence interval coverage. It is worth checking that imputations generate the correct collinearities among covariates.

With MICE and aregImpute we are using the chained Q equation approach (White et al., 2011) R
Chained equations handles a wide variety of target variables to be imputed and allows for multiple variables to be missing on the same subject
Iterative process cycles through all target variables to impute all missing values (S. van Buuren et al., 2006)
Does not attempt to use the full Bayesian multivariate model for all target variables, making it more flexible and easy to use
Possible to create improper imputations, e.g., imputing conflicting values for different target variables
However, simulation studies (S. van Buuren et al., 2006) demonstrate very good performance of imputation based on chained equations

3.9 Likelihood Ratio Tests and Multiple Imputation

For frequentist-based analysis Wald tests are ultimately unsatisfying for reasons detailed in Section 9.4
- Also it was never clear that simple averaging of $\hat{\beta}$ over completed datasets is the best approach
Chan & Meng (2022) have developed a promising approach to obtaining approximate LRT (likelihood ratio tests) in the presence of missing data
- Web site
- arXiv paper
- R code
- See Wood et al. (2008) for related work
Instead of averaging $M$ $\hat{\beta}$ from multiple separate analyses of completed datasets, stacks all completed datasets into one large dataset and computes maximum likelihood estimates on the one large stacked dataset
Divide LR $\chi^2$ by $M$ to get a rough estimate of the more correct LR described below; need to multiply by a discounting factor to take imputation into account
Individual fit LRs are used to derive imputation correction factors and the fraction of missing information
Chan and Meng have a formula that provides more accuate $p$-values by solving for denominator degrees of freedom for an $F$ distribution
- The degrees of freedom must be computed separately for each hypothesis test
- Accounts for heavier tail problem mentioned earlier
- $F$ test denominator d.f. is $\frac{k (M - 1)}{\hat{f}^{2}}$ where $k$ is the numerator d.f. (number of parameters being tested simultaneously), the fraction of missing information $\hat{f} = \frac{\hat{r}}{1+\hat{r}}$, $\hat{r} = \max(0, \frac{M+1}{k(M-1)} (\bar{d} - \hat{d}))$, where $\bar{d}$ is the mean over imputed datasets of the individual LR statistics and $\hat{d}$ is LR on the stacked dataset, divided by $M$
- Use large $M$ to make the $\chi^2$ approximation better by making the denominator d.f. larger. E.g., if $k=1$ and $\hat{f}=0.5$, $M=26$ already yields more than 100 denominator d.f. for $F$, making it hard to distinguish from a $\chi_{1}^{2}$ distribution. If the test statistic is 4.0, the $p$-value $\chi_{1}^{2}$ is 0.0455 and is 0.048 from $F_{1, 100}$.
Hmisc fit.mult.impute function run with lrt=TRUE runs and saves all the needed LR tests to allow rms processMI to compute everything else
processMI computes $\hat{f}$, the $F$ test denominator d.f., and the $\chi^2$ discount factor and uses these to get the final imputation-adjusted LR tests
fit.mult.impute computes approximate Wald statistics by multiplying the variance-covariance matrix computed on the stacked data by $M$ if individual completed dataset analyses are not done (not recommended)
Chan and Meng approach uses $\hat{\beta}$ computed once on stacked data as the MLE in the multiple imputation context; fit.mult.impute computes the final $\hat{\beta}$ this way if stacking is done; however the variance-covariance matrix is estimated from Rubin’s rule as in the Wald approach first used in this chapter
Imputation-adjusted LRTs can be a large computational burden for large datasets—for $M$ imputations, $j$ effects being tested requires $(M+1) j$ model fits. For each imputation, the rms anova function has very litle overhead though, due to it only computing the design matrix once, and calling low-level fitting functions for all LRTs once the overall model is fitted with a high-level function.

Example

Code

require(rms)
set.seed(1)
n <- 500
x1 <- runif(n)
x2 <- runif(n)
L  <- x1 + 2*x2
y  <- rbinom(n, 1, plogis(L))
x2[1:300] <- NA   # make 300 observations have missing x2
d <- data.frame(x1, x2, y)
a <- aregImpute(~ y + x1 + x2, n.impute=10, data=d, pr=FALSE)
f <- fit.mult.impute(y ~ x1 + x2, lrm, a, data=d, pr=FALSE)
f

Logistic Regression Model

fit.mult.impute(formula = y ~ x1 + x2, fitter = lrm, xtrans = a, 
    data = d, pr = FALSE)

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 500	LR χ² 48.78	R² 0.150	C 0.725
0 93	d.f. 2	R²_2,500 0.089	D_xy 0.451
1 407	Pr(>χ²) <0.0001	R²_2,227.1 0.183	γ 0.451
max \|∂log L/∂β\| 3×10^-7		Brier 0.138	τ_a 0.137

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-0.2395	0.4788	-0.50	0.6169
x1	1.6851	0.4804	3.51	0.0005
x2	2.2036	0.8701	2.53	0.0113

In the above results, the LR $\chi^2$ did not account for imputation and is too high. So are the $R^2$ measures derived from it.

Compute Wald $\chi^2$ test statistics accounting for imputation

Code

anova(f)

Wald Statistics for `y`
	χ²	d.f.	P
x1	12.30	1	0.0005
x2	6.41	1	0.0113
TOTAL	15.96	2	0.0003

Now compute LR test statistics accounting for imputation

Code

# lrt=TRUE makes fit.mult.impute set up all the arguments needed for LR tests
h <- fit.mult.impute(y ~ x1 + x2, lrm, a, data=d, lrt=TRUE, pr=FALSE)
h

Logistic Regression Model

fit.mult.impute(formula = y ~ x1 + x2, fitter = lrm, xtrans = a, 
    data = d, lrt = TRUE, pr = FALSE)

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 500	LR χ² 45.74	R² 0.142	C 0.724
0 93	d.f. 2	R²_2,5000 0.087	D_xy 0.449
1 407	Pr(>χ²) <0.0001	R²_2,2271.1 0.182	γ 0.449
max \|∂log L/∂β\| 7×10^-14		Brier 0.139	τ_a 0.136

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-0.2047	0.4788	-0.43	0.6690
x1	1.6607	0.4804	3.46	0.0005
x2	2.1519	0.8701	2.47	0.0134

Code

as <- processMI(h, which='anova')  # LR tests accounting for imputation
as

Likelihood Ratio Statistics for `y`
	χ²	d.f.	P
x1	10.23	1	0.0014
x2	6.30	1	0.0121
TOTAL	16.01	2	0.0003

Code

prmiInfo(as)

Imputation penalties
Test	Missing Information Fraction	Denominator d.f.	χ² Discount
x1	0.336	79.5	0.664
x2	0.788	14.5	0.212
TOTAL	0.650	42.6	0.350

The Chan & Meng $F$ approximation (processMI uses the $\chi^2$ version of it) is needed for x2 as the denominator d.f. of 14.5 is too low for $p$-values from the $\chi^2$ distribution to well approximate those from the $F$ distribution. Increase the number of imputations to increase the denominator d.f.

Code

a <- aregImpute(~ y + x1 + x2, n.impute=50, data=d, pr=FALSE)
h <- fit.mult.impute(y ~ x1 + x2, lrm, a, data=d, lrt=TRUE, pr=FALSE)
h

Logistic Regression Model

fit.mult.impute(formula = y ~ x1 + x2, fitter = lrm, xtrans = a, 
    data = d, lrt = TRUE, pr = FALSE)

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 500	LR χ² 40.49	R² 0.126	C 0.712
0 93	d.f. 2	R²_2,25000 0.078	D_xy 0.425
1 407	Pr(>χ²) <0.0001	R²_2,11355.3 0.163	γ 0.425
max \|∂log L/∂β\| 2×10^-13		Brier 0.141	τ_a 0.129

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-0.0783	0.3986	-0.20	0.8443
x1	1.5982	0.4640	3.44	0.0006
x2	1.9308	0.7341	2.63	0.0085

Code

as <- processMI(h, which='anova')
as

Likelihood Ratio Statistics for `y`
	χ²	d.f.	P
x1	12.10	1	0.0005
x2	6.74	1	0.0094
TOTAL	17.51	2	0.0002

Code

prmiInfo(as)

Imputation penalties
Test	Missing Information Fraction	Denominator d.f.	χ² Discount
x1	0.153	2097.1	0.847
x2	0.724	93.4	0.276
TOTAL	0.568	304.2	0.432

What happens if we use an extremely high number of imputations?

Code

a <- aregImpute(~ y + x1 + x2, n.impute=500, data=d, pr=FALSE)
h <- fit.mult.impute(y ~ x1 + x2, lrm, a, data=d, lrt=TRUE, pr=FALSE)
h

Logistic Regression Model

fit.mult.impute(formula = y ~ x1 + x2, fitter = lrm, xtrans = a, 
    data = d, lrt = TRUE, pr = FALSE)

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 500	LR χ² 42.41	R² 0.132	C 0.717
0 93	d.f. 2	R²_2,250000 0.081	D_xy 0.433
1 407	Pr(>χ²) <0.0001	R²_2,113553 0.170	γ 0.433
max \|∂log L/∂β\| 5×10^-12		Brier 0.140	τ_a 0.131

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-0.1123	0.3900	-0.29	0.7734
x1	1.5950	0.4688	3.40	0.0007
x2	2.0122	0.7207	2.79	0.0052

Code

as <- processMI(h, which='anova')
as

Likelihood Ratio Statistics for `y`
	χ²	d.f.	P
x1	11.12	1	0.0009
x2	7.85	1	0.0051
TOTAL	19.45	2	<0.0001

Code

prmiInfo(as)

Imputation penalties
Test	Missing Information Fraction	Denominator d.f.	χ² Discount
x1	0.218	10542.2	0.782
x2	0.702	1011.3	0.298
TOTAL	0.541	3405.6	0.459

3.10 Diagnostics

MCAR can be partially assessed by comparing distribution of S non-missing $Y$ for those subjects with complete $X$ vs. those subjects having incomplete $X$ (Little & Rubin, 2002)
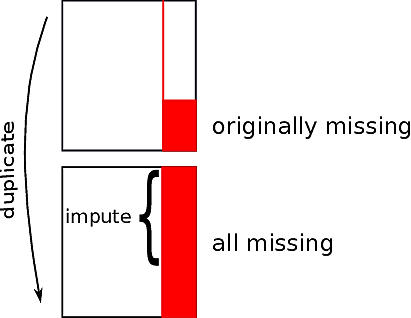
Yucel and Zaslavsky (Yucel & Zaslavsky, 2008; see also He & Zaslavsky, 2012)
Interested in reasonableness of imputed values for a sometimes-missing predictor $X_{j}$
Duplicate entire dataset
In the duplicated observations set all non-missing values of $X_{j}$ to missing; let $w$ denote this set of observations set to missing
Develop imputed values for the missing values of $X_{j}$
In the observations in $w$ compare the distribution of imputed $X_{j}$ to the original values of $X_{j}$
Bondarenko & Raghunathan (2016) present a variety of useful diagnostics on the reasonableness of imputed values.

3.11 Summary and Rough Guidelines

Table 3.1: Summary of methods for dealing with missing values

Method:	Deletion	Single	Multiple
Allows non-random missing		x	x
Reduces sample size	x
Apparent S.E. of $\hat{\beta}$ too low		x
Increases real S.E. of $\hat{\beta}$	x
$\hat{\beta}$ biased	if not MCAR	x

The following contains crude guidelines. Simulation studies are needed to refine the recommendations. Here $f$ refers to the proportion of observations having any variables missing.

$f < 0.03$: U It doesn’t matter very much how you impute missings or whether you adjust variance of regression coefficient estimates for having imputed data in this case. For continuous variables imputing missings with the median non-missing value is adequate; for categorical predictors the most frequent category can be used. Complete case analysis is also an option here. Multiple imputation may be needed to check that the simple approach “worked.”
$f \geq 0.03$: Use multiple imputation with number of imputations⁷ equal to $\max(5, 100f)$. Fewer imputations may be possible with very large sample sizes. See statisticalhorizons.com/how-many-imputations. Type 1 predictive mean matching is usually preferred, with weighted selection of donors. Account for imputation in estimating the covariance matrix for final parameter estimates. Use the $t$ distribution instead of the Gaussian distribution for tests and confidence intervals, if possible, using the estimated d.f. for the parameter estimates.
Multiple predictors frequently missing: V More imputations may be required. Perform a “sensitivity to order” analysis by creating multiple imputations using different orderings of sometimes missing variables. It may be beneficial to initially sort variables so that the one with the most NAs will be imputed first. aregImpute cycles in the order the analyst specifies variables in the formula.

⁷ White et al. (2011) recommend choosing $M$ so that the key inferential statistics are very reproducible should the imputation analysis be repeated. They suggest the use of $100f$ imputations. See also (Stef Buuren, 2012, sec. 2.7). von Hippel (2016) finds that the number of imputations should be quadratically increasing with the fraction of missing information.

Reason for missings more important than number of missing values.

Extreme amount of missing data does not prevent one from using multiple imputation, because alternatives are worse (Janssen et al., 2010; Madley-Dowd et al., 2019).

3.11.1 Effective Sample Size

It is useful to look at examples of effective sample sizes in the presence of missing data. If a sample of 1000 subjects contains various amounts and patterns of missings what size $n_c$ of a complete sample would have equivalent information for the intended purpose of the analysis?

A new marker was collected on a random sample of 200 of the subjects and one wants to estimate the added predictive value due to the marker: $n_{c}=200$ W
Height is missing on 100 subjects but we want to study association between BMI and outcome. Weight, sex, and waist circumference are available on all subjects: $n_{c}=980$
Each of 10 predictors is randomly missing on $\frac{1}{10}$ of subjects, and the predictors are uncorrelated with each other and are each weakly related to the outcome: $n_{c}=500$
Same as previous but the predictors can somewhat be predicted from non-missing predictors: $n_{c}=750$
The outcome variable was not assessed on a random $\frac{1}{5}$ of subjects: $n_{c}=800$
The outcome represents sensitive information, is missing on $\frac{1}{2}$ of subjects, and we don’t know what made subjects respond to the question: $n_{c}=0$ (serious selection bias)
One of the baseline variables was collected prospectively $\frac{1}{2}$ of the time and for the other subjects it was retrospectively estimated only for subjects ultimately suffering a stroke and we don’t know which subjects had a stroke: $n_{c}=0$ (study not worth doing)
The outcome variable was assessed by emailing the 1000 subjects, for which 800 responded, and we don’t know what made subjects respond: $n_{c}=0$ (model will possibly be very biased—at least the intercept)

3.12 Bayesian Methods for Missing Data

Multiple imputation developed as an approximation to a full X Bayesian model
Full Bayesian model treats missings as unknown parameters and provides exact inference and correct measures of uncertainty
See this case study for an example
The case study also shows how to do “posterior stacking” if you want to avoid having to specify a full model for missings, and instead use usual multiple imputations as described in this chapter. See Zhou & Reiter (2012).
- Run a multiple imputation algorithm
- For each completed dataset run the Bayesian analysis and draw thousands of samples from the posterior distribution of the parameters
- Pool all these posterior draws over all the multiple imputations and do posterior inference as usual with no special correction required
- Made easy by the Hmisc package aregImpute function and the rms stackMI function as demonstrated in the Titanic case study later in the notes.

3.13 Study Questions

Section 3.1

What is the problem with doing ordinary analysis of data from survey responders?

Section 3.4

What problem is always present when doing complete-case analysis when missing values exist in the data?
What problem is often present?
Why does imputation not help very much when a variable being imputed is a main variable of interest in the analysis?
What is a major reason that adding a new category for a predictor for missings doesn’t work?
Why does inserting a constant for missing values of a continuous predictor primarily fail?

Section 3.5

What is a more accurate statement than “imputation boosts the sample size”?
What does single-value fill-in of missings almost always damage?
What is a general way to describe why predictive mean matching (PMM) works?
What is a general advantage of PMM?

Section 3.6

Why does single conditional mean imputation result in biased regression coefficients?

Section 3.8

Why can multiple imputation use Y in predicting X?
What are the sources of uncertainty that a multiple imputation algorithm must take into account for final standard errors to not be underestimated?

Section 3.9

Explain the Yucel-Zaslavsky diagnosic and what it is checking for.

Section 3.10

What is the only reason not to always do 100 or more imputations?

Section 3.11

If using multiple imputation but within a Bayesian framework, what is a major advantage of posterior stacking over what we have been doing in the frequentist domain?

Allison, P. D. (2001). Missing Data. Sage.

Barnes, S. A., Lindborg, S. R., & Seaman, J. W. (2006). Multiple imputation techniques in small sample clinical trials. Stat Med, 25, 233–245.

bad performance of LOCF including high bias and poor confidence interval coverage;simulation setup;longitudinal data;serial data;RCT;dropout;assumed missing at random (MAR);approximate Bayesian bootstrap;Bayesian least squares;missing data;nice background summary;new completion score method based on fitting a Poisson model for the number of completed clinic visits and using donors and approximate Bayesian bootstrap

Barzi, F., & Woodward, M. (2004). Imputations of missing values in practice: Results from imputations of serum cholesterol in 28 cohort studies. Am J Epi, 160, 34–45.

excellent review article for multiple imputation;list of variables to include in imputation model;"Imputation models should ideally include all covariates that are related to the missing data mechanism, have distributions that differ between the respondents and nonrespondents, are associated with cholesterol, and will be included in the analyses of the final complete data sets";detailed comparison of results (cholesterol effect and confidence limits) for various imputation methods

Bondarenko, I., & Raghunathan, T. (2016). Graphical and numerical diagnostic tools to assess suitability of multiple imputations and imputation models. Stat Med, 35(17), 3007–3020. https://doi.org/10.1002/sim.6926

Buuren, Stef. (2012). Flexible imputation of missing data. Chapman & Hall/CRC. https://doi.org/10.1201/b11826

Carpenter, J. R., & Smuk, M. (2021). Missing data: A statistical framework for practice. Biometrical Journal, 63(5), 915–947. https://doi.org/10.1002/bimj.202000196

Chan, K. W., & Meng, X.-L. (2022). Multiple improvements of multiple imputation likelihood ratio tests. Statistica Sinica, 32, 1489–1514. https://doi.org/10.5705/ss.202019.0314

Crawford, S. L., Tennstedt, S. L., & McKinlay, J. B. (1995). A comparison of analytic methods for non-random missingness of outcome data. J Clin Epi, 48, 209–219.

Donders, van der Heijden, G. J. M. G., Stijnen, T., & Moons, K. G. M. (2006). Review: A gentle introduction to imputation of missing values. J Clin Epi, 59, 1087–1091.

simple demonstration of failure of the add new category method (indicator variable)

Erler, N. S., Rizopoulos, D., Rosmalen, J., Jaddoe, V. W. V., Franco, O. H., & Lesaffre, E. M. E. H. (2016). Dealing with missing covariates in epidemiologic studies: A comparison between multiple imputation and a full Bayesian approach. Stat Med, 35(17), 2955–2974. https://doi.org/10.1002/sim.6944

Harel, O., & Zhou, X.-H. (2007). Multiple imputation: Review of theory, implementation and software. Stat Med, 26, 3057–3077.

failed to review aregImpute;excellent overview;ugly S code;nice description of different statistical tests including combining likelihood ratio tests (which appears to be complex, requiring an out-of-sample log likelihood computation);congeniality of imputation and analysis models;Bayesian approximation or approximate Bayesian bootstrap overview;"Although missing at random (MAR) is a non-testable assumption, it has been pointed out in the literature that we can get very close to MAR if we include enough variables in the imputation models ... it would be preferred if the missing data modelling was done by the data constructors and not by the users... MI yields valid inferences not only in congenial settings, but also in certain uncongenial ones as well—where the imputer’s model (1) is more general (i.e. makes fewer assumptions) than the complete-data estimation method, or when the imputer’s model makes additional assumptions that are well-founded."

Hazewinkel, A., Tilling, K., Wade, K. H., & Palmer, T. (2023). Trial arm outcome variance difference after dropout as an indicator of missing‐not‐at‐random bias in randomized controlled trials. Biometrical J, 2200116. https://doi.org/10.1002/bimj.202200116

Indirect assessment of MNAR by comparing variances of continuous outcome variable. Not sure if authors discussed transformation assumptions about Y.

He, Y., & Zaslavsky, A. M. (2012). Diagnosing imputation models by applying target analyses to posterior replicates of completed data. Stat Med, 31(1), 1–18. https://doi.org/10.1002/sim.4413

Horton, N. J., & Kleinman, K. P. (2007). Much ado about nothing: A comparison of missing data methods and software to fit incomplete data regression models. Am Statistician, 61(1), 79–90.

Janssen, K. J., Donders, A. R., Harrell, F. E., Vergouwe, Y., Chen, Q., Grobbee, D. E., & Moons, K. G. (2010). Missing covariate data in medical research: To impute is better than to ignore. J Clin Epi, 63, 721–727.

Jones, M. P. (1996). Indicator and stratification methods for missing explanatory variables in multiple linear regression. J Am Stat Assoc, 91, 222–230.

Kim, S., Sugar, C. A., & Belin, T. R. (2015). Evaluating model-based imputation methods for missing covariates in regression models with interactions. Stat Med, 34(11), 1876–1888. https://doi.org/10.1002/sim.6435

Knol, M. J., Janssen, K. J. M., Donders, R. T., Egberts, A. C. G., Heerding, E. R., Grobbee, D. E., Moons, K. G. M., & Geerlings, M. I. (2010). Unpredictable bias when using the missing indicator method or complete case analysis for missing confounder values: An empirical example. J Clin Epi, 63, 728–736.

Lee, K. J., & Carlin, J. B. (2012). Recovery of information from multiple imputation: A simulation study. Emerg Themes Epi, 9(1), 3+. https://doi.org/10.1186/1742-7622-9-3

Not sure that the authors satisfactorily dealt with nonlinear predictor effectsin the absence of strong auxiliary information, there is little to gain from multiple imputation with missing data in the exposure-of-interest. In fact, the authors went further to say that multiple imputation can introduce bias not present in a complete case analysis if a poorly fitting imputation model is used [from Yong Hao Pua]

Lipsitz, S., Parzen, M., & Zhao, L. P. (2002). A Degrees-Of-Freedom approximation in Multiple imputation. J Stat Comp Sim, 72(4), 309–318. https://doi.org/10.1080/00949650212848

Little, R. J. A., & Rubin, D. B. (2002). Statistical Analysis with Missing Data (second). Wiley.

Madley-Dowd, P., Hughes, R., Tilling, K., & Heron, J. (2019). The proportion of missing data should not be used to guide decisions on multiple imputation. Journal of Clinical Epidemiology, 110, 63–73. https://doi.org/10.1016/j.jclinepi.2019.02.016

Mamouris, P., Nassiri, V., Verbeke, G., Janssens, A., Vaes, B., & Molenberghs, G. (2023). A longitudinal transition imputation model for categorical data applied to a large registry dataset. Statistics in Medicine, 42(29), 5405–5418. https://doi.org/10.1002/sim.9919

Moons, K. G. M., Donders, R. A. R. T., Stijnen, T., & Harrell, F. E. (2006). Using the outcome for imputation of missing predictor values was preferred. J Clin Epi, 59, 1092–1101. https://doi.org/10.1016/j.jclinepi.2006.01.009

use of outcome variable; excellent graphical summaries of simulations

Penning, de V. B. B. L., van, S. M., & Groenwold, R. H. H. (2018). Propensity Score Estimation Using Classification and Regression Trees in the Presence of Missing Covariate Data. Epidemiologic Methods, 7(1). https://doi.org/10.1515/em-2017-0020

Reiter, J. P. (2007). Small-sample degrees of freedom for multi-component significance tests with multiple imputation for missing data. Biometrika, 94(2), 502–508. https://doi.org/10.1093/biomet/asm028

Rubin, D., & Schenker, N. (1991). Multiple imputation in health-care data bases: An overview and some applications. Stat Med, 10, 585–598.

Schafer, J. L., & Graham, J. W. (2002). Missing data: Our view of the state of the art. Psych Meth, 7, 147–177.

excellent review and overview of missing data and imputation;problems with MICE;less technical description of 3 types of missing data

Sullivan, T. R., Salter, A. B., Ryan, P., & Lee, K. J. (2015). Bias and Precision of the “Multiple Imputation, Then Deletion” Method for Dealing With Missing Outcome Data. American Journal of Epidemiology, 182(6), 528–534. https://doi.org/10.1093/aje/kwv100

Disagrees with von Hippel approach of "impute then delete" for Y

Twisk, J., de Boer, M., de Vente, W., & Heymans, M. (2013). Multiple imputation of missing values was not necessary before performing a longitudinal mixed-model analysis. J Clin Epi, 66(9), 1022–1028. https://doi.org/10.1016/j.jclinepi.2013.03.017

Vach, W., & Blettner, M. (1998). Missing Data in Epidemiologic Studies. In Ency of Biostatistics (pp. 2641–2654). Wiley.

van Buuren, S., Brand, J. P. L., Groothuis-Oudshoorn, C. G. M., & Rubin, D. B. (2006). Fully conditional specification in multivariate imputation. J Stat Computation Sim, 76(12), 1049–1064.

justification for chained equations alternative to full multivariate modeling

van der Heijden, G. J. M. G., Donders, Stijnen, T., & Moons, K. G. M. (2006). Imputation of missing values is superior to complete case analysis and the missing-indicator method in multivariable diagnostic research: A clinical example. J Clin Epi, 59, 1102–1109. https://doi.org/10.1016/j.jclinepi.2006.01.015

Invalidity of adding a new category or an indicator variable for missing values even with MCAR

Vink, G., Frank, L. E., Pannekoek, J., & van Buuren, S. (2014). Predictive mean matching imputation of semicontinuous variables. Statistica Neerlandica, 68(1), 61–90. https://doi.org/10.1111/stan.12023

von Hippel, P. T. (2007). Regression with missing Ys: An improved strategy for analyzing multiple imputed data. Soc Meth, 37(1), 83–117.

von Hippel, P. T. (2016). The number of imputations should increase quadratically with the fraction of missing information. http://arxiv.org/abs/1608.05406

White, I. R., & Carlin, J. B. (2010). Bias and efficiency of multiple imputation compared with complete-case analysis for missing covariate values. Stat Med, 29, 2920–2931.

White, I. R., & Royston, P. (2009). Imputing missing covariate values for the Cox model. Stat Med, 28, 1982–1998.

approach to using event time and censoring indicator as predictors in the imputation model for missing baseline covariates;recommended an approximation using the event indicator and the cumulative hazard transformation of time, without their interaction

White, I. R., Royston, P., & Wood, A. M. (2011). Multiple imputation using chained equations: Issues and guidance for practice. Stat Med, 30(4), 377–399.

practical guidance for the use of multiple imputation using chained equations;MICE;imputation models for different types of target variables;PMM choosing at random from among a few closest matches;choosing number of multiple imputations by a reproducibility argument, suggesting 100f imputations when f is the fraction of cases that are incomplete

Wood, A. M., White, I. R., & Royston, P. (2008). How should variable selection be performed with multiply imputed data? Statistics in Medicine, 27(17), 3227–3246. https://doi.org/10.1002/sim.3177

Yucel, R. M., & Zaslavsky, A. M. (2008). Using calibration to improve rounding in imputation. Am Statistician, 62(2), 125–129.

using rounding to impute binary variables using techniques for continuous data;uses the method to solve for the cutpoint for a continuous estimate to be converted into a binary value;method should be useful in more general situations;idea is to duplicate the entire dataset and in the second half of the new datasets to set all non-missing values of the target variable to missing;multiply impute these now-missing values and compare them to the actual values

Zhou, X., & Reiter, J. P. (2012). A Note on Bayesian Inference After Multiple Imputation. The American Statistician, 64(2), 159–163. https://doi.org/10.1198/tast.2010.09109