10 Binary Logistic Regression

\(Y=0, 1\)
Time of event not important
In \(C(Y|X)\) \(C\) is \(\Pr(Y=1)\)
\(g(u)\) is \(\frac{1}{1+e^{-u}} = \text{expit}(u)\)

10.1 Model

\[ \Pr(Y=1|X) = [1+\exp(-X\beta)]^{-1} \]

\[ P = [1+\exp(-x)]^{-1} = \text{expit}(x) \]

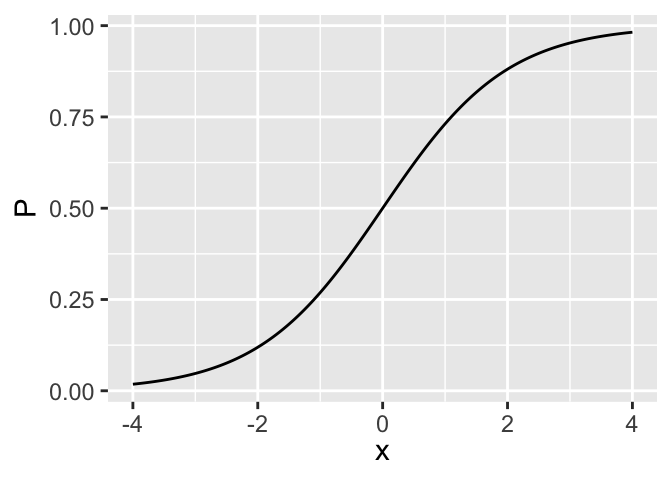
\(O = \frac{P}{1-P}\)
\(P = \frac{O}{1+O}\)
\(X\beta = \log\frac{P}{1-P} = \text{logit}(P)\)
\(e^{X\beta} = O\)

10.1.1 Model Assumptions and Interpretation of Parameters

\[\begin{array}{ccc} \text{logit}(Y=1|X) &=& \text{logit}(P) = \log\frac{P}{1-P} \nonumber \\ &=& X\beta , \end{array}\]

Increase \(X_{j}\) by \(d\) \(\rightarrow\) increase odds \(Y=1\) by \(\exp(\beta_{j}d)\), increase log odds by \(\beta_{j}d\).
If there is only one predictor \(X\) and that predictor is binary, the model can be written

\[\begin{array}{ccc} \text{logit}(Y=1|X=0) &=& \beta_{0} \nonumber \\ \text{logit}(Y=1|X=1) &=& \beta_{0}+\beta_{1} . \end{array}\]

One continuous predictor: \[ \text{logit}(Y=1|X) = \beta_{0}+\beta_{1} X, \]
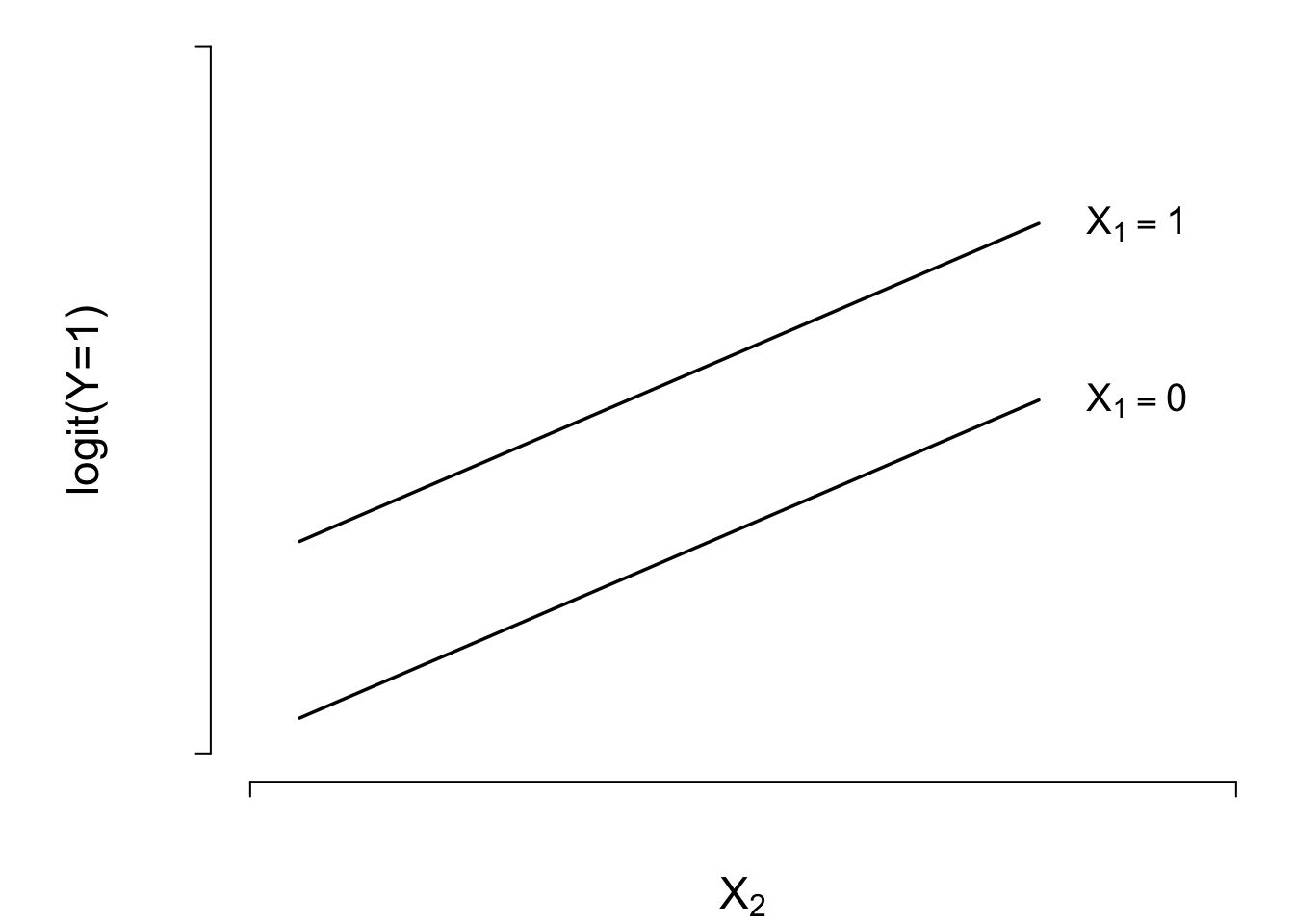
Two treatments (indicated by \(X_{1}=0\) or \(1\)) and one continuous covariable (\(X_{2}\)). \[ \text{logit}(Y=1|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2} , \]

\[\begin{array}{ccc} \text{logit}(Y=1|X_{1}=0, X_{2}) &=& \beta_{0}+\beta_{2}X_{2} \nonumber \\ \text{logit}(Y=1|X_{1}=1, X_{2}) &=& \beta_{0}+\beta_{1}+\beta_{2}X_{2} . \end{array}\]

10.1.2 Odds Ratio, Risk Ratio, and Risk Difference

Odds ratio capable of being constant
Ex: risk factor doubles odds of disease

Without Risk Factor		With Risk Factor
Probability	Odds	Odds	Probability
0.20	0.25	0.5	0.333
0.50	1.00	2.0	0.667
0.80	4.00	8.0	0.889
0.90	9.00	18.0	0.947
0.98	49.00	98.0	0.990

Code

spar(bty='l')
plot(0, 0, type="n", xlab="Risk for Subject Without Risk Factor",
     ylab="Increase in Risk",
     xlim=c(0,1), ylim=c(0,.6))
i <- 0
or <- c(1.1,1.25,1.5,1.75,2,3,4,5,10)
for(h in or) {
  i <- i + 1
  p <- seq(.0001, .9999, length=200)
  logit <- log(p/(1 - p))  # same as qlogis(p)
  logit <- logit + log(h)  # modify by odds ratio
  p2 <- 1/(1 + exp(-logit))# same as plogis(logit)
  d <- p2 - p
  lines(p, d, lty=i)
  maxd <- max(d)
  smax <- p[d==maxd]
  text(smax, maxd + .02, format(h), cex=.6)
}

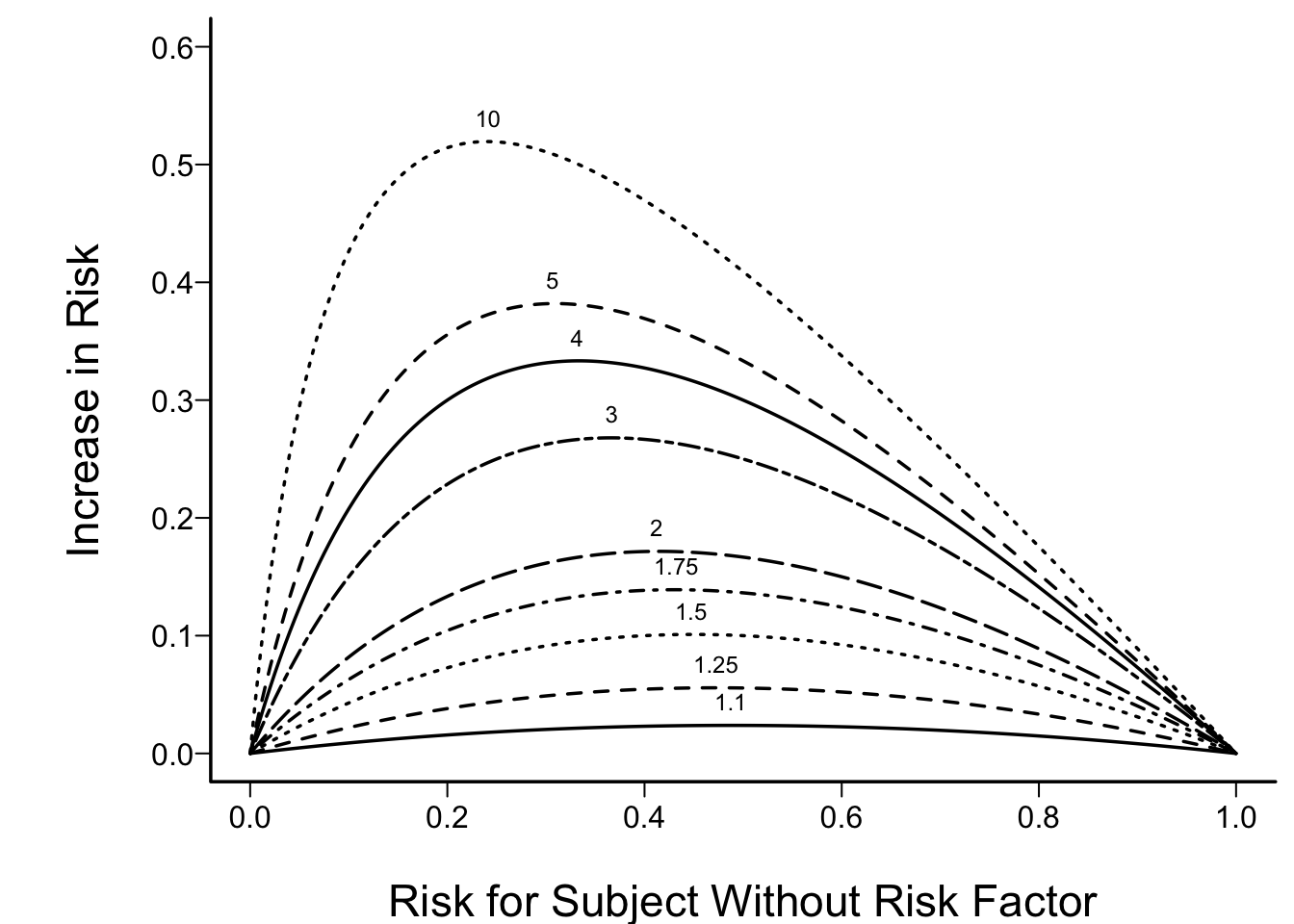
Figure 10.2: Absolute benefit as a function of risk of the event in a control subject and the relative effect (odds ratio) of the risk factor. The odds ratios are given for each curve.

Let \(X_{1}\) be a binary risk factor and let
\(A=\{X_{2},\ldots,X_{p}\}\) be the other factors. Then the estimate of \(\Pr(Y=1|X_{1}=1, A) -\) \(\Pr(Y=1|X_{1}=0, A)\) is

\[\begin{array}{c} \frac{1}{1+\exp-[\hat{\beta_{0}}+\hat{\beta_{1}}+\hat{\beta_{2}}X_{2}+\ldots+\hat{\beta_{p}}X_{p}]} \nonumber \\ - \frac{1}{1+\exp-[\hat{\beta_{0}}+\hat{\beta_{2}}X_{2}+\ldots +\hat{\beta_{p}}X_{p}]} \\ = \frac{1}{1+(\frac{1-\hat{R}}{\hat{R}}) \exp(-\hat{\beta}_{1})} - \hat{R}, \nonumber \end{array}\]

where \(R=\Pr(Y=1|X_{1}=0, A)\).

Risk ratio is \(\frac{1+e^{-X_{2}\beta}}{1+e^{-X_{1}\beta}}\)
Does not simplify like odds ratio, which is \(\frac{e^{X_{1}\beta}}{e^{X_{2}\beta}} = e^{(X_{1}-X_{2})\beta}\)

10.1.3 Detailed Example

Age: Females	37	39	39	42	47	48	48	52	53	55	56	57	58	58	60	64	65	68	68	70
Response:	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	1	1	1	1
Age: Males	34	38	40	40	41	43	43	43	44	46	47	48	48	50	50	52	55	60	61	61
Response:	1	1	0	0	0	1	1	1	0	0	1	1	1	0	1	1	1	1	1	1

Code

require(rms)
options(prType='html')     # output format for certain rms functions
getHdata(sex.age.response)
d <- as.data.table(sex.age.response)  # so can do easy aggregation
dd <- datadist(d); options(datadist='dd')
f <- lrm(response ~ sex + age, data=d)
fasr <- f   # Save for later
p <- Predict(f, age=seq(34, 70, length=200), sex, fun=plogis)
# Function to bin a variable and represent bin by mean x within bin
mb <- function(x, ...) as.numeric(as.character(cut2(x, ..., levels.mean=TRUE)))
d[, ageg := mb(age, cuts=c(45, 55))]
props <- d[, .(prop = mean(response)), by=.(ageg, sex)]
ggplot(p, ylab='Pr(response)') +
  geom_point(data=d, aes(x=age, y=response, color=sex)) +
  geom_point(data=props, aes(x=ageg, y=prop, color=sex, shape=I(2)))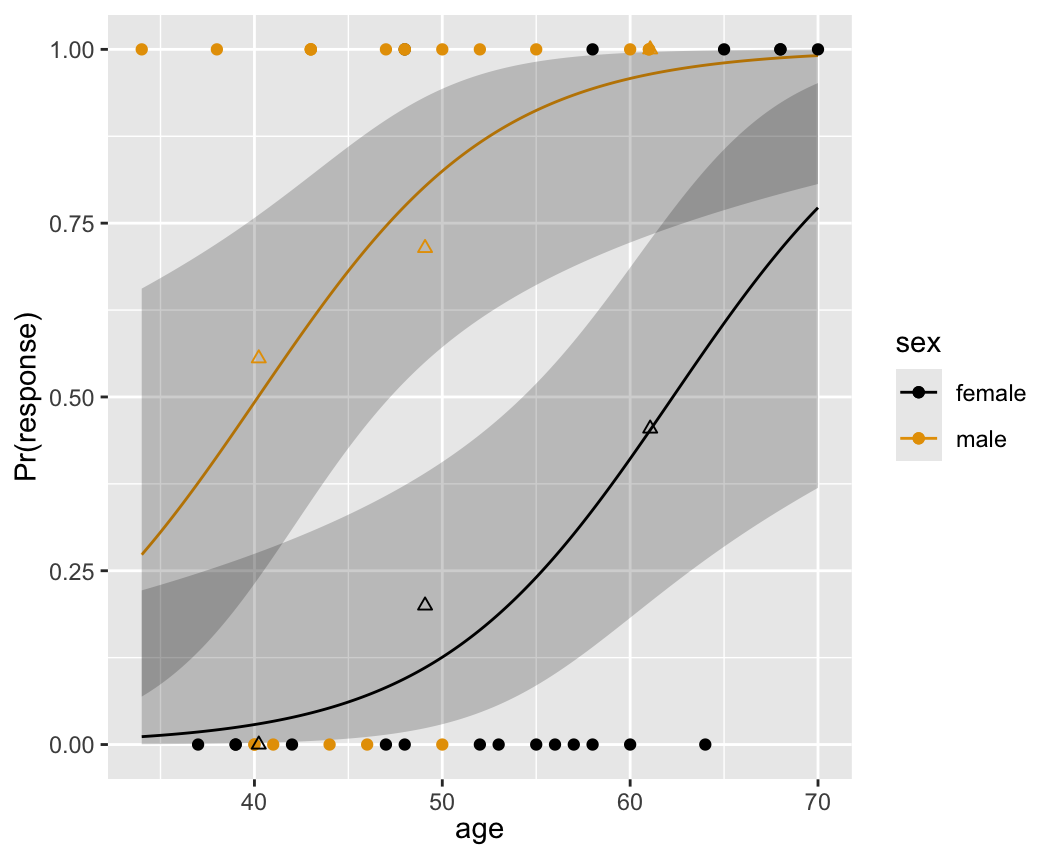

Figure 10.3: Data, subgroup proportions (triangles), and fitted logistic model, with 0.95 pointwise confidence bands

Code

ltx <- function(fit) {
  w <- latex(fit, inline=TRUE, columns=54,
             after='', digits=3,
             before='$$X\\hat{\\beta}=$$')
    rendHTML(w, html=FALSE)
  }
ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -9.84\\ +3.49[\mathrm{male}] +0.158\:\mathrm{age} \end{array}\]


                 sex        response
                 Frequency
                 Row Pct      0        1    Total     Odds/Log

                 F           14        6       20    6/14=.429
                          70.00    30.00                 -.847

                 M            6       14       20    14/6=2.33
                          30.00    70.00                  .847

                 Total       20       20       40

                M:F odds ratio = (14/6)/(6/14) = 5.44, log=1.695

sex \(\times\) response
Statistic	DF	Value	Prob
Wald \(\chi^2\)	1	6.400	0.011
Likelihood Ratio \(\chi^2\)	1	6.583	0.010

Parameter	Estimate	Std Err	Wald \(\chi^{2}\)	P
\(\beta_{0}\)	-0.847	0.488	3.015
\(\beta_{1}\)	1.695	0.690	6.030	0.014

Log likelihood (\(\beta_{1}=0\))	-27.727
Log likelihood (max)	-24.435
LR \(\chi^{2} (H_{0}:\beta_{1}=0)\) -2(-27.727- -24.435) = 6.584

Next, consider the relationship between age and response, ignoring sex.

                 age        response
                 Frequency
                 Row Pct      0        1    Total     Odds/Log

                 <45          8        5       13     5/8=.625
                           61.5     38.4                  -.47

                 45-54        6        6       12        6/6=1
                           50.0     50.0                     0

                 55+          6        9       15      9/6=1.5
                           40.0     60.0                  .405

                 Total       20       20       40

                55+ : <45 odds ratio = (9/6)/(5/8) = 2.4, log=.875

Parameter	Estimate	Std Err	Wald \(\chi^{2}\)	P
\(\beta_{0}\)	-2.734	1.838	2.213
\(\beta_{1}\)	0.054	0.036	2.276	0.131

The estimate of \(\beta_{1}\) is in rough agreement with that obtained from the frequency table. The 55+:<45 log odds ratio is .875, and since the respective mean ages in the 55+ and <45 age groups are 61.1 and 40.2, an estimate of the log odds ratio increase per year is .875/(61.1 - 40.2)=.875/20.9=.042.

The likelihood ratio test for \(H_{0}\): no association between age and response is obtained as follows:

Log likelihood (\(\beta_{1}=0\))	-27.727
Log likelihood (max)	-26.511
LR \(\chi^{2} (H_{0}:\beta_{1}=0)\)	-2(-27.727- -26.511) = 2.432

(Compare 2.432 with the Wald statistic 2.28.)

Next we consider the simultaneous association of age and sex with response.


                                 sex=F

                 age        response
                 Frequency
                 Row Pct      0        1    Total

                 <45          4        0        4
                          100.0      0.0

                 45-54        4        1        5
                           80.0     20.0

                 55+          6        5       11
                           54.6     45.4

                 Total       14        6       20


                                 sex=M

                 age        response
                 Frequency
                 Row Pct      0        1    Total

                 <45          4        5        9
                           44.4     55.6

                 45-54        2        5        7
                           28.6     71.4

                 55+          0        4        4
                            0.0    100.0

                 Total        6       14       20

A logistic model for relating sex and age simultaneously to response is given below.

Parameter	Estimate	Std Err	Wald \(\chi^{2}\)	P
\(\beta_{0}\)	-9.843	3.676	7.171
\(\beta_{1}\) (sex)	3.490	1.199	8.469	0.004
\(\beta_{2}\) (age)	0.158	0.062	6.576	0.010

Likelihood ratio tests are obtained from the information below.

Log likelihood (\(\beta_{1}=0,\beta_{2}=0\))	-27.727
Log likelihood (max)	-19.458
Log likelihood (\(\beta_{1}=0\))	-26.511
Log likelihood (\(\beta_{2}=0\))	-24.435
LR \(\chi^{2}\) (\(H_{0}:\beta_{1}=\beta_{2}=0\))	-2(-27.727- -19.458)= 16.538
LR \(\chi^{2}\) (\(H_{0}:\beta_{1}=0\)) sex\(\|\)age	-2(-26.511- -19.458) = 14.106
LR \(\chi^{2}\) (\(H_{0}:\beta_{2}=0\)) age\(\|\)sex	-2(-24.435- -19.458) = 9.954

The 14.1 should be compared with the Wald statistic of 8.47, and 9.954 should be compared with 6.58. Likelihood ratio tests may be obtained automatically starting in rms version 6.7-0, as follows.

Code

f <- update(f, x=TRUE, y=TRUE)   # LR tests require raw data in fits
anova(f, test='LR')

Likelihood Ratio Statistics for `response`
	χ²	d.f.	P
sex	14.11	1	0.0002
age	9.95	1	0.0016
TOTAL	16.54	2	0.0003

The fitted logistic model is plotted separately for females and males in Figure 10.3 .

The fitted model is

\[\Pr(\text{Response=1}|\text{sex,age}) = \text{expit}(-9.84+3.49\times \text{sex} +.158\times \text{age})\]

where as before sex=0 for females, 1 for males. For example, for a 40 year old female, the predicted logit is \(-9.84+.158(40) = -3.52\). The predicted probability of a response is \(\text{expit}(3.52)= .029\). For a 40 year old male, the predicted logit is \(-9.84 + 3.49+.158(40) = -.03\), with a probability of .492.

10.1.4 Design Formulations

Can do ANOVA using \(k-1\) dummies for a \(k\)-level predictor
Can get same \(\chi^2\) statistics as from a contingency table
Can go farther: covariable adjustment
Simultaneous comparison of multiple variables between two groups: Turn problem backwards to predict group from all the dependent variables
This is more robust than a parametric multivariate test
Propensity scores for adjusting for nonrandom treatment selection: Predict treatment from all baseline variables
Adjusting for the predicted probability of getting a treatment adjusts adequately for confounding from all of the variables
In a randomized study, using logistic model to adjust for covariables, even with perfect balance, will improve the treatment effect estimate

10.2 Estimation

10.2.1 Maximum Likelihood Estimates

Like binomial case but \(P\)s vary; \(\hat{\beta}\) computed by trial and error using an iterative maximization technique

10.2.2 Estimation of Odds Ratios and Probabilities

\[\hat{P}_{i} = \text{expit}(X_{i}\hat{\beta})\]

\[\text{expit}(X_{i}\hat{\beta}\pm zs)\]

10.2.3 Minimum Sample Size Requirement

Categorical Predictor Case

Simplest case: no covariates, only an intercept
Consider margin of error of 0.1 in estimating \(\theta = \Pr(Y=1)\) with 0.95 confidence
Worst case: \(\theta = \frac{1}{2}\)
Requires \(n=96\) observations¹
Single binary predictor with prevalence \(\frac{1}{2}\): need \(n=96\) for each value of \(X\)
For margin of error of \(\pm 0.05, n=384\) is required (if true probabilities near 0.5 are possible); \(n=246\) required if true probabilities are only known not to be in \([0.2, 0.8]\).

¹ The general formula for the sample size required to achieve a margin of error of \(\delta\) in estimating a true probability of \(\theta\) at the 0.95 confidence level is \(n = (\frac{1.96}{\delta})^{2} \times \theta(1 - \theta)\). Set \(\theta = \frac{1}{2}\) for the worst case.

Single Continuous Predictor

Predictor \(X\) has a normal distribution with mean zero and standard deviation \(\sigma\), with true \(P = \text{expit}(X)\) so that the expected number of events is \(\frac{n}{2}\). Compute mean and 0.9 quantile of \(\max_{X \in [-1.5,1.5]} |P - \hat{P}|\) over 1000 simulations for varying \(n\) and \(\sigma\)²

² An average absolute error of 0.05 corresponds roughly to a 0.95 confidence interval margin of error of 0.1.

See this for more about R coding for simulations of this type.

Code

require(rms)
require(ggplot2)

g <- function() {
set.seed(12)
sigmas  <- c(.5, .75, 1, 1.25, 1.5, 1.75, 2, 2.5, 3, 4)
ns      <- seq(25, 500, by=25)
nsim    <- 1000
xs      <- seq(-1.5, 1.5, length=200)
pactual <- plogis(xs)

dn     <- list(sigma=format(sigmas), n=format(ns), sim=NULL)
maxerr <- array(NA, c(length(sigmas), length(ns), nsim), dn)

i <- 0
for(s in sigmas) {
  i <- i + 1
  j <- 0
  for(n in ns) {
    j <- j + 1
    for(k in 1:nsim) {
      x <- rnorm(n, 0, s)
      P <- plogis(x)
      y <- ifelse(runif(n) <= P, 1, 0)
      beta <- lrm.fit(x, y)$coefficients
      phat <- plogis(beta[1] + beta[2] * xs)
      maxerr[i, j, k] <- max(abs(phat - pactual))
    }
  }
}
f  <- function(x) c(Mean=mean(x), Q90=unname(quantile(x, probs=0.9)))
apply(maxerr, 1:2, f)   # summarize over 3rd dimension (1000 simulations)
}

me    <- runifChanged(g)
# Function to create a variable holding value for ith dimension
slice <- function(a, i) {
  dn <- all.is.numeric(dimnames(a)[[i]], 'vector')   # all.is.numeric in Hmisc
  dn[as.vector(slice.index(a, i))]
}
u <- data.frame(maxerr = as.vector(me),
                stat   = slice(me, 1),
                sigma  = slice(me, 2),
                n      = slice(me, 3))
ggplot(u, aes(x=n, y=maxerr, color=factor(sigma))) + geom_line() +
  facet_wrap(~ stat) +
  ylab(expression(max(abs(hat(P) - P)))) +
  guides(color=guide_legend(title=expression(sigma))) +
  theme(legend.position='bottom')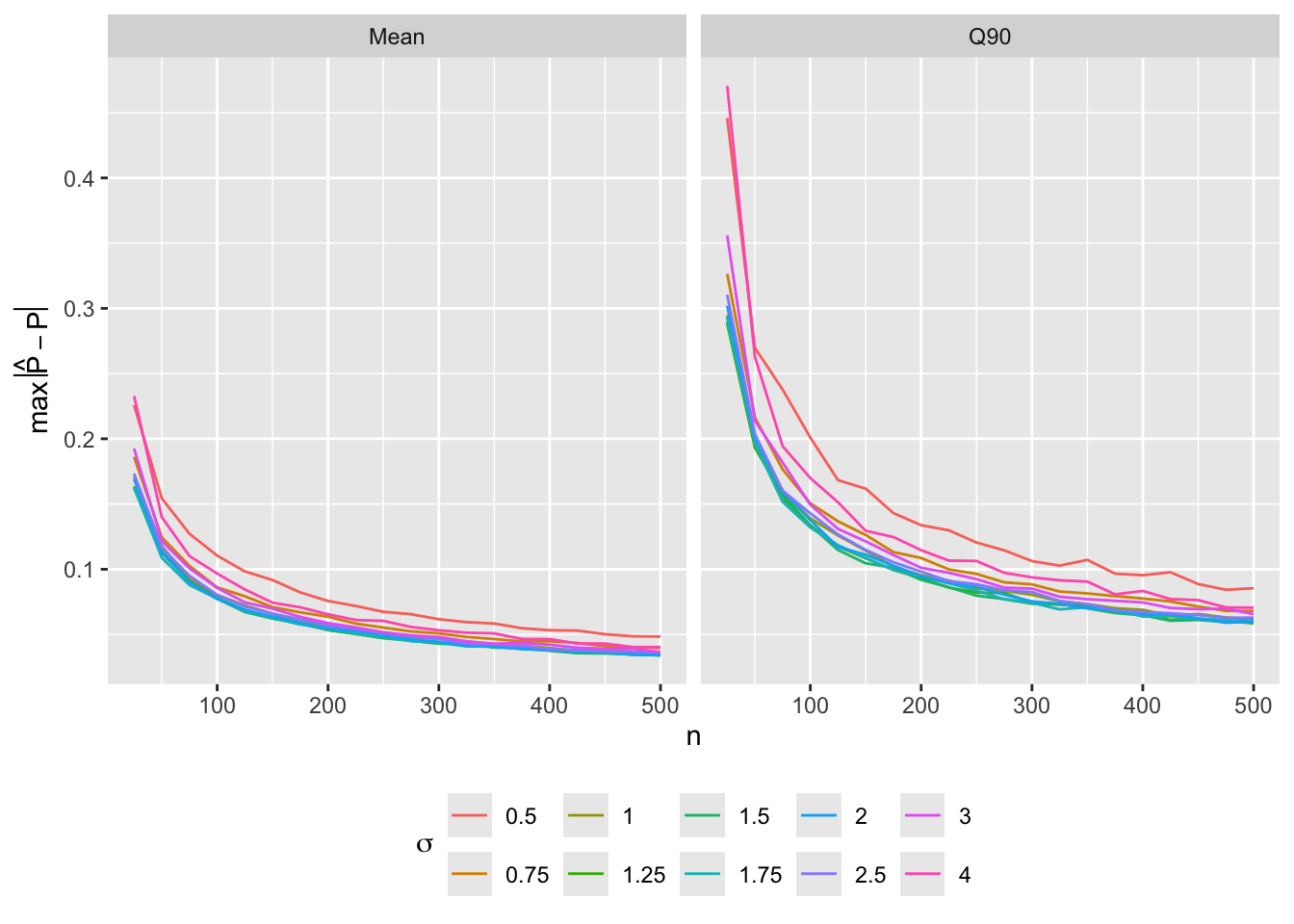

Figure 10.4: Simulated expected and 0.9 quantile of the maximum error in estimating probabilities for \(x \in [-1.5, 1.5]\) with a single normally distributed \(X\) with mean zero

10.3 Test Statistics

Likelihood ratio test best
Score test second best (score \(\chi^{2} \equiv\) Pearson \(\chi^2\))
Wald test may misbehave but is quick

10.4 Residuals

Partial residuals (to check predictor transformations)

\[r_{ij} = \hat{\beta}_{j}X_{ij} + \frac{Y_{i} - \hat{P}_{i}}{\hat{P}_{i}(1-\hat{P}_{i})}\]

10.5 Assessment of Model Fit

\[\text{logit}(Y=1|X) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}\]

Figure 10.5: Logistic regression assumptions for one binary and one continuous predictor

Code

getHdata(acath)
acath$sex <- factor(acath$sex, 0:1, c('male','female'))
dd <- datadist(acath); options(datadist='dd')
f <- lrm(sigdz ~ rcs(age, 4) * sex, data=acath)
kn <- specs(f)$how.modeled['age','Parameters']
kn <- setdiff(strsplit(kn, ' ')[[1]], '')
kn[length(kn)] <- paste('and', kn[length(kn)])
kn <- paste(kn, collapse=', ')

Code

d <- as.data.table(acath)
d[, ageg := mb(age, g=10)]   # bin into deciles of age
# Compute logit of proportion of disease in each decile and sex group
binned <- d[, .(logitprop = qlogis(mean(sigdz))), by=.(ageg, sex)]
# Estimate loess curves separately by sex
# Function to compute logit of loess nonparametric estimates for binary y
loel <- function(x, y, xlim) {
  j <- ! is.na(x + y)
  x <- x[j]; y <- y[j]
  z <- lowess(x, y, iter=0)
  i <- if(missing(xlim)) TRUE else z$x >= xlim[1] & z$x <= xlim[2]
  list(x=z$x[i], y=qlogis(z$y[i]))
}
loe <- d[, loel(age, sigdz, xlim=c(25, 78)), by=.(sex)]
ggplot(Predict(f, age, sex)) +
  geom_point(data=binned, aes(x=ageg, y=logitprop, color=sex, shape=I(2))) +
  geom_line(data=loe, aes(x=x, y=y, color=sex, linetype=I(2)))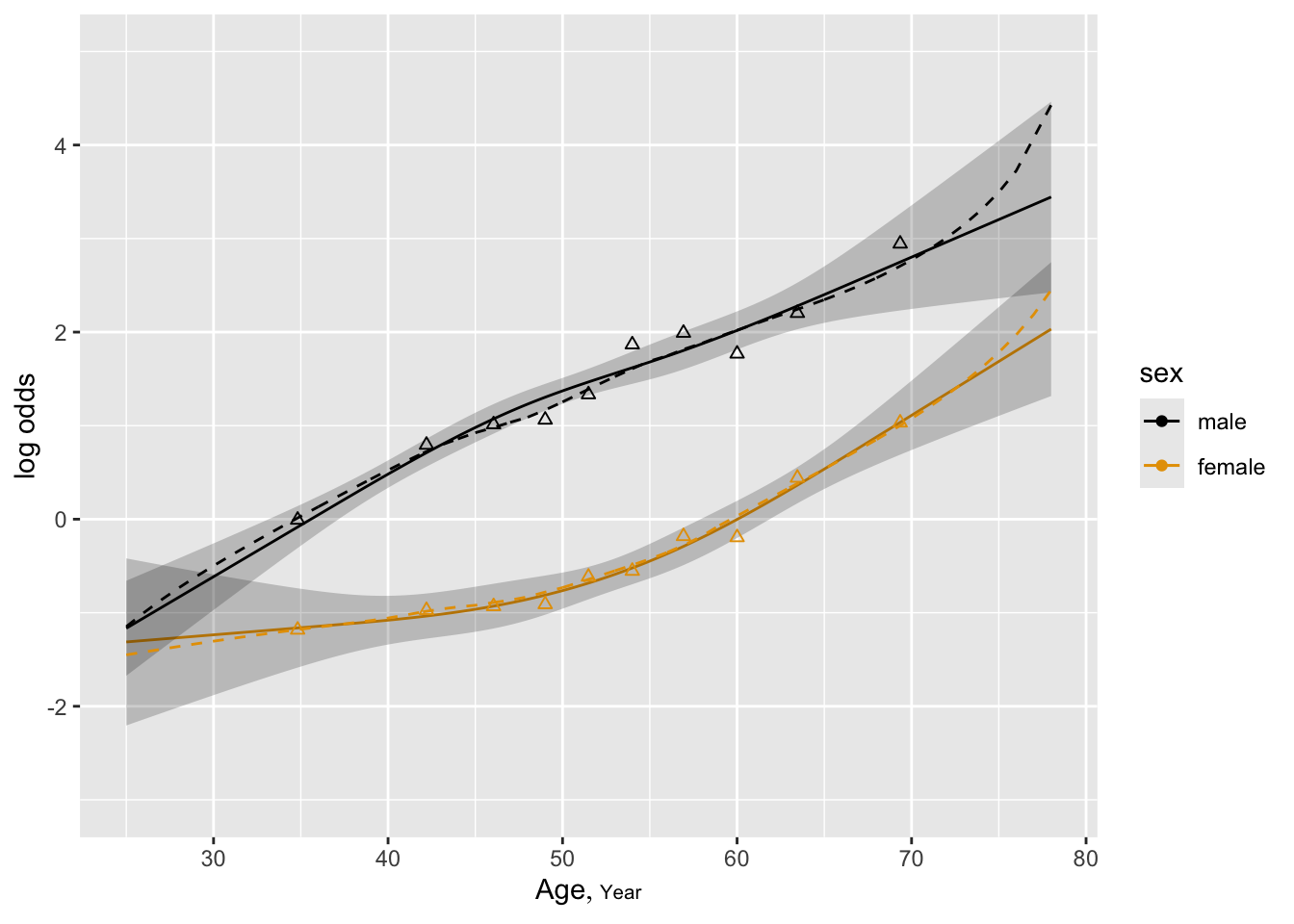

Figure 10.6: Logit proportions of significant coronary artery disease by sex and deciles of age for n=3504 patients, with spline fits (smooth curves). Spline fits are for \(k=4\) knots at age=36, 48, 56, and 68 years, and interaction between age and sex is allowed. Shaded bands are pointwise 0.95 confidence limits for predicted log odds. Smooth nonparametric estimates are shown as dashed lines. Data courtesy of the Duke Cardiovascular Disease Databank.

Can verify by plotting stratified proportions
\(\hat{P}\) = number of events divided by stratum size
\(\hat{O} = \frac{\hat{P}}{1-\hat{P}}\)
Plot \(\log \hat{O}\) (scale on which linearity is assumed)
Stratified estimates are noisy
1 or 2 \(X\)s \(\rightarrow\) nonparametric smoother
Use loess to compute logits of nonparametric estimates (fun=qlogis)
General: restricted cubic spline expansion of one or more predictors

\[\begin{array}{ccc} \text{logit}(Y=1|X) &=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+\hat{\beta}_{2}X_{2}+\hat{\beta}_{3}X_{2}'+\hat{\beta}_{4}X_{2}'' \nonumber \\ &=& \hat{\beta}_{0}+\hat{\beta}_{1}X_{1}+f(X_{2}) , \end{array}\] \[\begin{array}{ccc} \text{logit}(Y=1|X) &=& \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{2}'+\beta_{4}X_{2}'' \nonumber \\ && +\beta_{5}X_{1}X_{2}+\beta_{6}X_{1}X_{2}'+\beta_{7}X_{1}X_{2}'' \end{array}\]

Code

lr <- function(formula)
  {
    f <- lrm(formula, data=acath)
    stats <- f$stats[c('Model L.R.', 'd.f.')]
    cat('L.R. Chi-square:', round(stats[1],1),
        '  d.f.:', stats[2],'\n')
    f
  }
a <- lr(sigdz ~ sex + age)

L.R. Chi-square: 766   d.f.: 2

Code

b <- lr(sigdz ~ sex * age)

L.R. Chi-square: 768.2   d.f.: 3

Code

c <- lr(sigdz ~ sex + rcs(age,4))

L.R. Chi-square: 769.4   d.f.: 4

Code

d <- lr(sigdz ~ sex * rcs(age,4))

L.R. Chi-square: 782.5   d.f.: 7

Code

lrtest(a, b)


Model 1: sigdz ~ sex + age
Model 2: sigdz ~ sex * age

L.R. Chisq       d.f.          P 
 2.1964146  1.0000000  0.1383322

Code

lrtest(a, c)


Model 1: sigdz ~ sex + age
Model 2: sigdz ~ sex + rcs(age, 4)

L.R. Chisq       d.f.          P 
 3.4502500  2.0000000  0.1781508

Code

lrtest(a, d)


Model 1: sigdz ~ sex + age
Model 2: sigdz ~ sex * rcs(age, 4)

  L.R. Chisq         d.f.            P 
16.547036344  5.000000000  0.005444012

Code

lrtest(b, d)


Model 1: sigdz ~ sex * age
Model 2: sigdz ~ sex * rcs(age, 4)

  L.R. Chisq         d.f.            P 
14.350621767  4.000000000  0.006256138

Code

lrtest(c, d)


Model 1: sigdz ~ sex + rcs(age, 4)
Model 2: sigdz ~ sex * rcs(age, 4)

  L.R. Chisq         d.f.            P 
13.096786352  3.000000000  0.004431906

Model / Hypothesis	Likelihood Ratio \(\chi^2\)	d.f.	\(P\)	Formula
a: sex, age (linear, no interaction)	766.0	2
b: sex, age, age \(\times\) sex	768.2	3
c: sex, spline in age	769.4	4
d: sex, spline in age, interaction	782.5	7
\(H_{0}:\) no age \(\times\) sex interaction given linearity	2.2	1	.14	(\(b-a\))
\(H_{0}:\) age linear \(\|\) no interaction	3.4	2	.18	(\(c-a\))
\(H_{0}:\) age linear, no interaction	16.6	5	.005	(\(d-a\))
\(H_{0}:\) age linear, product form interaction	14.4	4	.006	(\(d-b\))
\(H_{0}:\) no interaction, allowing for nonlinearity in age	13.1	3	.004	(\(d-c\))

Obtain all the fully adjusted likelihood ratio \(\chi^2\) tests automatically.

Code

f <- lrm(sigdz ~ sex * rcs(age,4), data=acath, x=TRUE, y=TRUE)
anova(f, test='LR')

Likelihood Ratio Statistics for `sigdz`
	χ²	d.f.	P
sex (Factor+Higher Order Factors)	555.62	4	<0.0001
All Interactions	13.10	3	0.0044
age (Factor+Higher Order Factors)	358.90	6	<0.0001
All Interactions	13.10	3	0.0044
Nonlinear (Factor+Higher Order Factors)	14.35	4	0.0063
sex × age (Factor+Higher Order Factors)	13.10	3	0.0044
Nonlinear	9.67	2	0.0080
Nonlinear Interaction : f(A,B) vs. AB	9.67	2	0.0080
TOTAL NONLINEAR	14.35	4	0.0063
TOTAL NONLINEAR + INTERACTION	16.55	5	0.0054
TOTAL	782.54	7	<0.0001

Example of finding transform. of a single continuous predictor
Duration of symptoms vs. odds of severe coronary disease
Look at AIC to find best # knots for the money

k	Model \(\chi^{2}\)	AIC
0	99.23	97.23
3	112.69	108.69
4	121.30	115.30
5	123.51	115.51
6	124.41	114.41

Code

d  <- as.data.table(acath)[sigdz == 1]
dd <- datadist(d)
f <- lrm(tvdlm ~ rcs(cad.dur, 5), data=d)
d[, durg := mb(cad.dur, g=15)]   # bin into 15-tiles of age
# Compute logit of proportion of severe dz in each bin
binned <- d[, .(logitprop = qlogis(mean(tvdlm))), by=.(durg)]
loe <- d[, loel(cad.dur, tvdlm, xlim=c(0, 326))]
ggplot(Predict(f, cad.dur)) +
  geom_point(data=binned, aes(x=durg, y=logitprop, shape=I(2))) +
  geom_line(data=loe, aes(x=x, y=y, linetype=I(2)))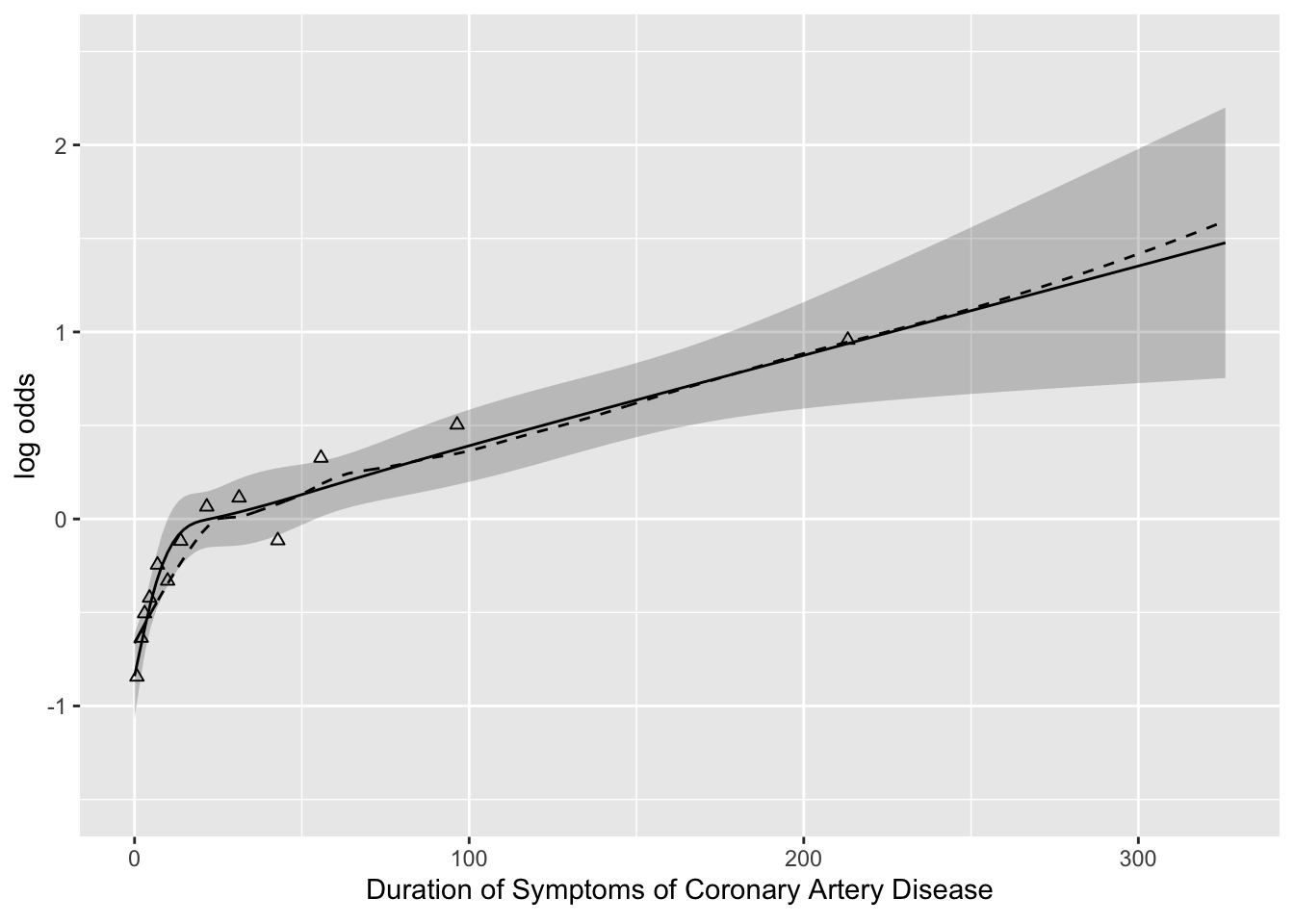

Figure 10.7: Estimated relationship between duration of symptoms and the log odds of severe coronary artery disease for \(k=5\). Knots are marked with arrows. Solid line is spline fit; dashed line is a nonparametric loess estimate. Triangles are logits of proportions after binning duration.

Code

f <- lrm(tvdlm ~ log10(cad.dur + 1), data=d)
binned <- d[, .(prop = mean(tvdlm)), by=.(durg)]
ggplot(Predict(f, cad.dur, fun=plogis), ylab='P') +
  geom_point(data=binned, aes(x=durg, y=prop, shape=I(2)))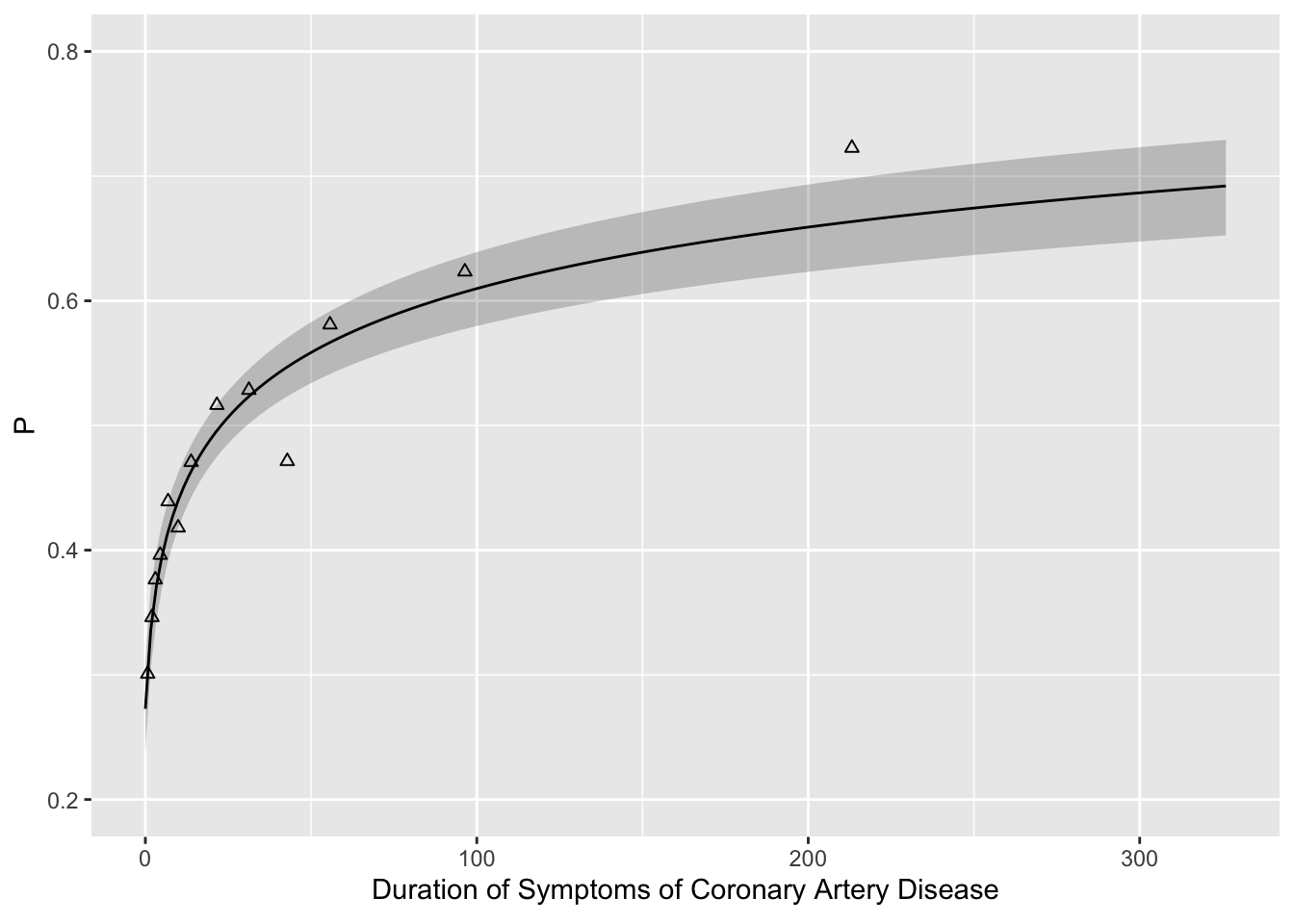

Figure 10.8: Fitted linear logistic model in \(\log_{10}(\text{duration + 1})\), with subgroup estimates using groups of 150 patients. Fitted equation is \(\Pr(\text{tvdlm})\) = \(\text{expit}(-.9809+.7122 \log_{10}(\text{months}+1))\).

Modeling Interaction Surfaces

Sample of 2258 pts³
Predict significant coronary disease
For now stratify age into tertiles to examine interactions simply
Model has 2 dummies for age, sex, age \(\times\) sex, 4-knot restricted cubic spline in cholesterol, age tertile \(\times\) cholesterol

³ Many patients had missing cholesterol.

Code

acath <- transform(acath,
                   cholesterol = choleste,
                   age.tertile = cut2(age, g=3),
                   sx = as.integer(acath$sex) - 1)
# sx for loess, need to code as numeric
dd <- datadist(acath); options(datadist='dd')

# First model stratifies age into tertiles to get more
# empirical estimates of age x cholesterol interaction

f <- lrm(sigdz ~ age.tertile*(sex + rcs(cholesterol,4)),
         data=acath)
f

Logistic Regression Model

lrm(formula = sigdz ~ age.tertile * (sex + rcs(cholesterol, 4)), 
    data = acath)

Frequencies of Missing Values Due to Each Variable

      sigdz age.tertile         sex cholesterol 
          0           0           0        1246

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 2258	LR χ² 533.52	R² 0.291	C 0.780
0 768	d.f. 14	R²_14,2258 0.206	D_xy 0.560
1 1490	Pr(>χ²) <0.0001	R²_14,1520.4 0.289	γ 0.560
max \|∂log L/∂β\| 2×10^-8		Brier 0.173	τ_a 0.251

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-0.4155	1.0987	-0.38	0.7053
age.tertile=[49,58)	0.8781	1.7337	0.51	0.6125
age.tertile=[58,82]	4.7861	1.8143	2.64	0.0083
sex=female	-1.6123	0.1751	-9.21	<0.0001
cholesterol	0.0029	0.0060	0.48	0.6347
cholesterol'	0.0384	0.0242	1.59	0.1126
cholesterol''	-0.1148	0.0768	-1.49	0.1350
age.tertile=[49,58) × sex=female	-0.7900	0.2537	-3.11	0.0018
age.tertile=[58,82] × sex=female	-0.4530	0.2978	-1.52	0.1283
age.tertile=[49,58) × cholesterol	0.0011	0.0095	0.11	0.9093
age.tertile=[58,82] × cholesterol	-0.0158	0.0099	-1.59	0.1111
age.tertile=[49,58) × cholesterol'	-0.0183	0.0365	-0.50	0.6162
age.tertile=[58,82] × cholesterol'	0.0127	0.0406	0.31	0.7550
age.tertile=[49,58) × cholesterol''	0.0582	0.1140	0.51	0.6095
age.tertile=[58,82] × cholesterol''	-0.0092	0.1301	-0.07	0.9436

Code

ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -0.415\\ +0.878[\mathrm{age.tertile} \in [49,58)]+4.79 [\mathrm{age.tertile} \in [58,82]]\\ -1.61[\mathrm{female}]\\+ 0.00287 \mathrm{cholesterol}+1.52\!\times\!10^{-6 }(\mathrm{cholesterol}-160)_{+}^{3} \\ -4.53\!\times\!10^{-6}(\mathrm{cholesterol}-208)_{+}^{3}+3.44\!\times\!10^{-6 }(\mathrm{cholesterol}-243)_{+}^{3} \\ -4.28\!\times\!10^{-7}(\mathrm{cholesterol}-319)_{+}^{3} \\+[\mathrm{female}][-0.79 \:[\mathrm{age.tertile} \in [49,58)]\\ -0.453\:[\mathrm{age.tertile} \in [58,82]] ]\\ +[\mathrm{age.tertile} \in [49,58)][0.00108 \mathrm{cholesterol} \\ -7.23\!\times\!10^{-7}(\mathrm{cholesterol}-160)_{+}^{3}+2.3\!\times\!10^{-6 }(\mathrm{cholesterol}-208)_{+}^{3} \\ -1.84\!\times\!10^{-6}(\mathrm{cholesterol}-243)_{+}^{3}+2.69\!\times\!10^{-7 }(\mathrm{cholesterol}-319)_{+}^{3} ]\\ +[\mathrm{age.tertile} \in [58,82]][-0.0158 \mathrm{cholesterol} \\ +5\!\times\!10^{-7 }(\mathrm{cholesterol}-160)_{+}^{3}-3.64\!\times\!10^{-7}(\mathrm{cholesterol}-208)_{+}^{3} \\ -5.15\!\times\!10^{-7}(\mathrm{cholesterol}-243)_{+}^{3}+3.78\!\times\!10^{-7 }(\mathrm{cholesterol}-319)_{+}^{3} ] \end{array}\]

Code

print(anova(f), caption='Crudely categorizing age into tertiles')

Crudely categorizing age into tertiles
	χ²	d.f.	P
age.tertile (Factor+Higher Order Factors)	120.74	10	<0.0001
All Interactions	21.87	8	0.0052
sex (Factor+Higher Order Factors)	329.54	3	<0.0001
All Interactions	9.78	2	0.0075
cholesterol (Factor+Higher Order Factors)	93.75	9	<0.0001
All Interactions	10.03	6	0.1235
Nonlinear (Factor+Higher Order Factors)	9.96	6	0.1263
age.tertile × sex (Factor+Higher Order Factors)	9.78	2	0.0075
age.tertile × cholesterol (Factor+Higher Order Factors)	10.03	6	0.1235
Nonlinear	2.62	4	0.6237
Nonlinear Interaction : f(A,B) vs. AB	2.62	4	0.6237
TOTAL NONLINEAR	9.96	6	0.1263
TOTAL INTERACTION	21.87	8	0.0052
TOTAL NONLINEAR + INTERACTION	29.67	10	0.0010
TOTAL	410.75	14	<0.0001

Code

yl <- c(-1,5)
ggplot(Predict(f, cholesterol, age.tertile),
       adj.subtitle=FALSE, ylim=yl)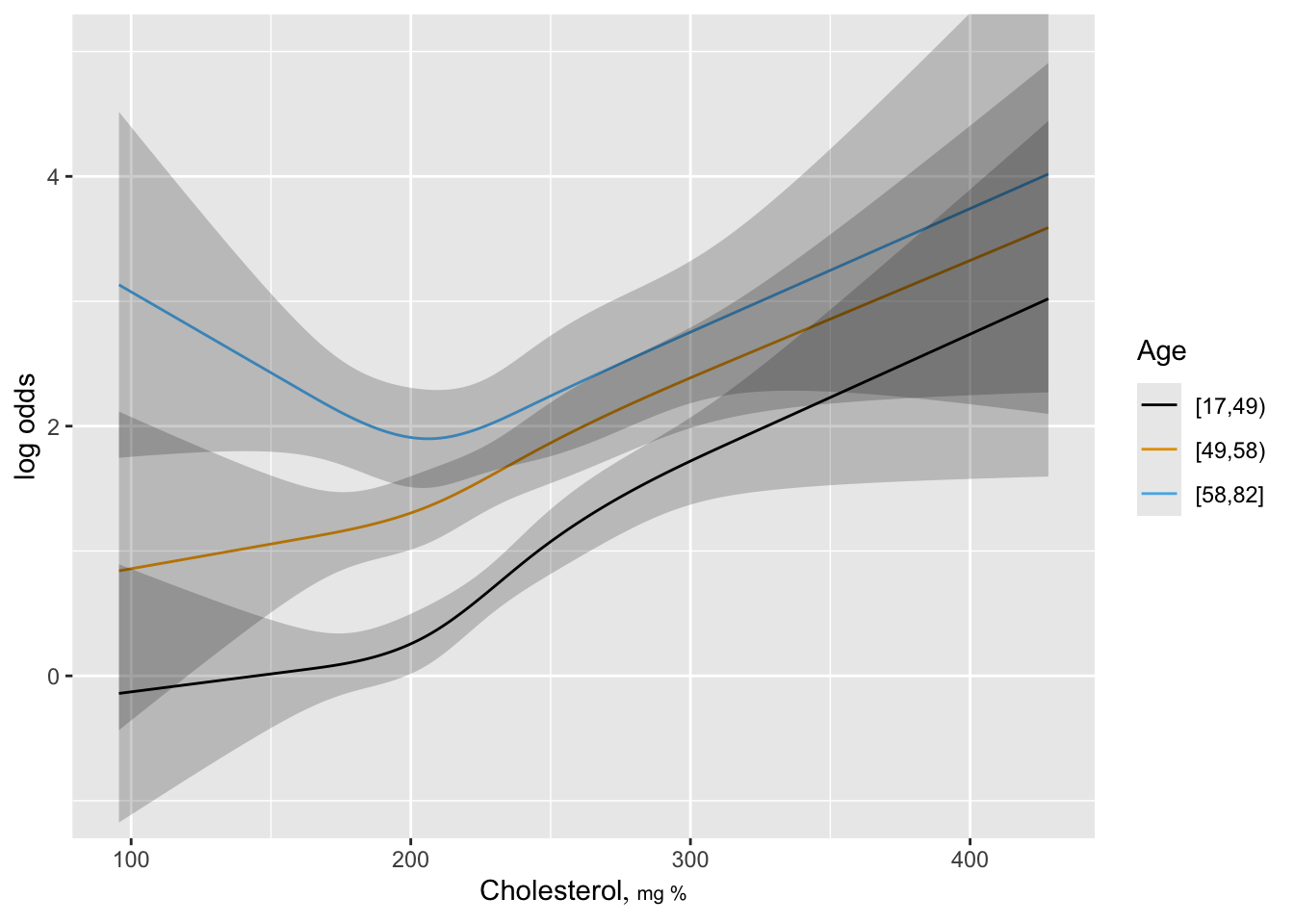

Figure 10.9: Log odds of significant coronary artery disease modeling age with two dummy variables

Now model age as continuous predictor
Start with nonparametric surface using \(Y=0/1\)

Code

# Re-do model with continuous age
require(lattice)   # provides wireframe
f <- loess(sigdz ~ age * (sx + cholesterol), data=acath,
           parametric="sx", drop.square="sx")
ages  <- seq(25,   75, length=40)
chols <- seq(100, 400, length=40)
g <- expand.grid(cholesterol=chols, age=ages, sx=0)
# drop sex dimension of grid since held to 1 value
p <- drop(predict(f, g))
p[p < 0.001] <- 0.001
p[p > 0.999] <- 0.999
zl <- c(-3, 6)
wireframe(qlogis(p) ~ cholesterol*age,
          xlab=list(rot=30), ylab=list(rot=-40),
          zlab=list(label='log odds', rot=90), zlim=zl,
          scales = list(arrows = FALSE), data=g)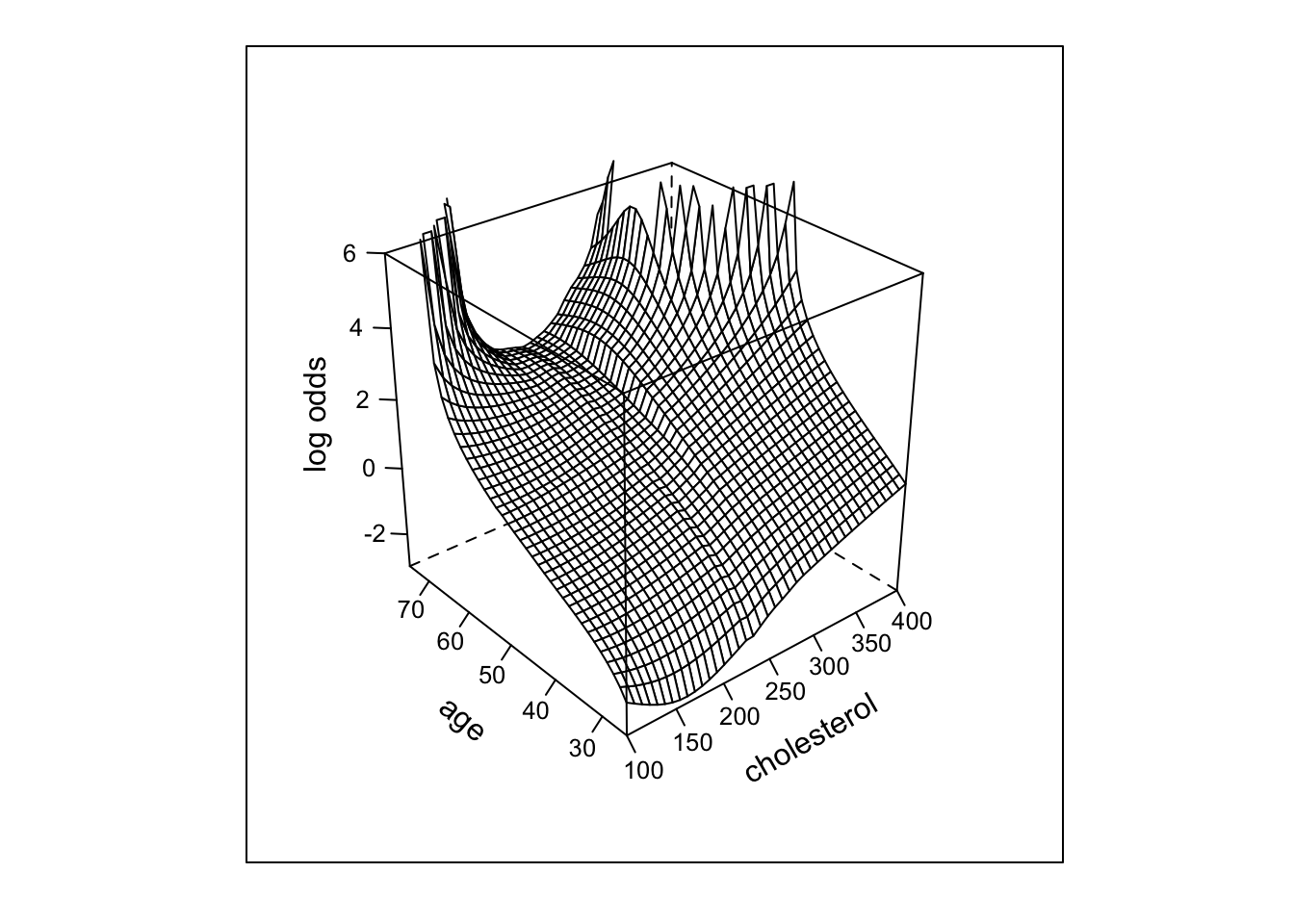

Figure 10.10: Local regression fit for the logit of the probability of significant coronary disease vs. age and cholesterol for males, based on the `loess` function.

Next try parametric fit using linear spline in age, chol. (3 knots each), all product terms. For all the remaining 3-d plots we limit plotting to points that are supported by at least 5 subjects beyond those cholesterol/age combinations

Code

f <- lrm(sigdz ~ lsp(age,c(46,52,59)) *
         (sex + lsp(cholesterol,c(196,224,259))),
         data=acath)
ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -1.83\\ +0.0232 \:\mathrm{age}+0.0759 (\mathrm{age}-46)_{+}-0.0025(\mathrm{age}-52)_{+}+2.27 (\mathrm{age}-59)_{+}\\ +3.02[\mathrm{female}]\\ -0.0177\:\mathrm{cholesterol}+0.114 (\mathrm{cholesterol}-196)_{+}\\ -0.131 (\mathrm{cholesterol}-224)_{+}+0.0651 (\mathrm{cholesterol}-259)_{+}\\+[\mathrm{female}][-0.112 \:\mathrm{age}+0.0852 \:(\mathrm{age}-46)_{+}-0.0302\:(\mathrm{age}-52)_{+}\\ +0.176 \:(\mathrm{age}-59)_{+} ]\\+\mathrm{age}[0.000577 \:\mathrm{cholesterol}-0.00286 \:(\mathrm{cholesterol}-196)_{+}\\+0.00382 \:(\mathrm{cholesterol}-224)_{+}-0.00205 \:(\mathrm{cholesterol}-259)_{+} ]\\+(\mathrm{age}-46)_{+}[-0.000936\:\mathrm{cholesterol}+0.00643 \:(\mathrm{cholesterol}-196)_{+}\\-0.0115 \:(\mathrm{cholesterol}-224)_{+}+0.00756 \:(\mathrm{cholesterol}-259)_{+} ]\\+(\mathrm{age}-52)_{+}[0.000433 \:\mathrm{cholesterol}-0.0037 \:(\mathrm{cholesterol}-196)_{+}\\+0.00815 \:(\mathrm{cholesterol}-224)_{+}-0.00715 \:(\mathrm{cholesterol}-259)_{+} ]\\+(\mathrm{age}-59)_{+}[-0.0124 \:\mathrm{cholesterol}+0.015 \:(\mathrm{cholesterol}-196)_{+}\\ -0.0067 \:(\mathrm{cholesterol}-224)_{+}+0.00752 \:(\mathrm{cholesterol}-259)_{+} ] \end{array}\]

Code

print(anova(f), caption='Linear spline surface')

Linear spline surface
	χ²	d.f.	P
age (Factor+Higher Order Factors)	164.17	24	<0.0001
All Interactions	42.28	20	0.0025
Nonlinear (Factor+Higher Order Factors)	25.21	18	0.1192
sex (Factor+Higher Order Factors)	343.80	5	<0.0001
All Interactions	23.90	4	<0.0001
cholesterol (Factor+Higher Order Factors)	100.13	20	<0.0001
All Interactions	16.27	16	0.4341
Nonlinear (Factor+Higher Order Factors)	16.35	15	0.3595
age × sex (Factor+Higher Order Factors)	23.90	4	<0.0001
Nonlinear	12.97	3	0.0047
Nonlinear Interaction : f(A,B) vs. AB	12.97	3	0.0047
age × cholesterol (Factor+Higher Order Factors)	16.27	16	0.4341
Nonlinear	11.45	15	0.7204
Nonlinear Interaction : f(A,B) vs. AB	11.45	15	0.7204
f(A,B) vs. Af(B) + Bg(A)	9.38	9	0.4033
Nonlinear Interaction in age vs. Af(B)	9.99	12	0.6167
Nonlinear Interaction in cholesterol vs. Bg(A)	10.75	12	0.5503
TOTAL NONLINEAR	33.22	24	0.0995
TOTAL INTERACTION	42.28	20	0.0025
TOTAL NONLINEAR + INTERACTION	49.03	26	0.0041
TOTAL	449.26	29	<0.0001

Code

perim <- with(acath,
              perimeter(cholesterol, age, xinc=20, n=5))
zl <- c(-2, 4)
bplot(Predict(f, cholesterol, age, np=40), perim=perim,
      lfun=wireframe, zlim=zl, adj.subtitle=FALSE)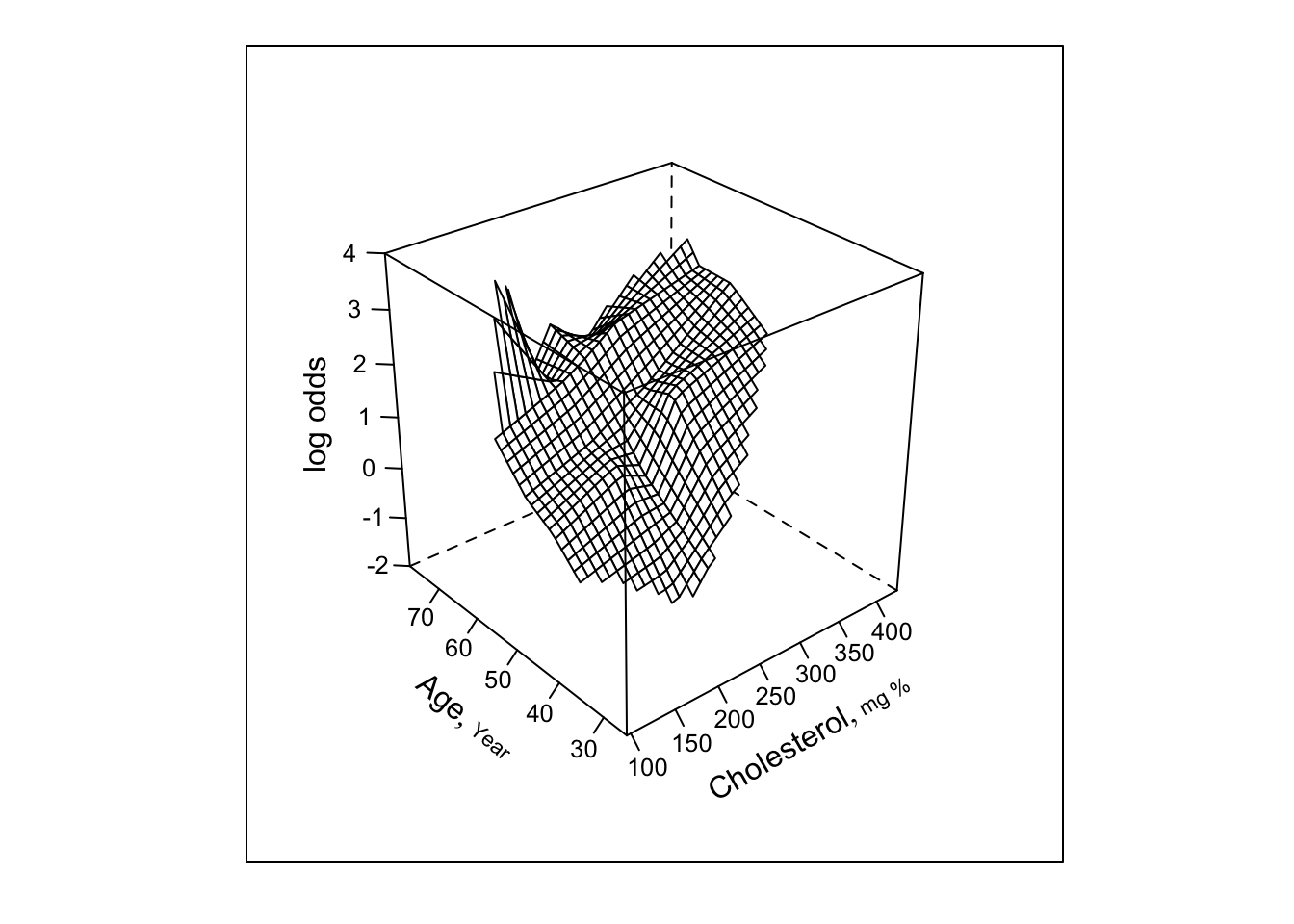

Figure 10.11: Linear spline surface for males, with knots for age at 46, 52, 59 and knots for cholesterol at 196, 224, and 259 (quartiles).

Next try smooth spline surface, include all cross-products

Code

f <- lrm(sigdz ~ rcs(age,4)*(sex + rcs(cholesterol,4)),
         data=acath, tol=1e-11)
ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -6.41\\+ 0.166 \mathrm{age}-0.00067(\mathrm{age}-36)_{+}^{3}+0.00543 (\mathrm{age}-48)_{+}^{3} \\ -0.00727(\mathrm{age}-56)_{+}^{3}+0.00251 (\mathrm{age}-68)_{+}^{3} \\ +2.87[\mathrm{female}]\\+ 0.00979 \mathrm{cholesterol}+1.96\!\times\!10^{-6 }(\mathrm{cholesterol}-160)_{+}^{3} \\ -7.16\!\times\!10^{-6}(\mathrm{cholesterol}-208)_{+}^{3}+6.35\!\times\!10^{-6 }(\mathrm{cholesterol}-243)_{+}^{3} \\ -1.16\!\times\!10^{-6}(\mathrm{cholesterol}-319)_{+}^{3} \\ +[\mathrm{female}][-0.109 \mathrm{age}+7.52\!\times\!10^{-5}(\mathrm{age}-36)_{+}^{3}+0.00015 (\mathrm{age}-48)_{+}^{3} \\ -0.00045(\mathrm{age}-56)_{+}^{3}+0.000225(\mathrm{age}-68)_{+}^{3} ]\\ +\mathrm{age}[-0.00028 \mathrm{cholesterol}+2.68\!\times\!10^{-9 }(\mathrm{cholesterol}-160)_{+}^{3} \\ +3.03\!\times\!10^{-8 }(\mathrm{cholesterol}-208)_{+}^{3}-4.99\!\times\!10^{-8}(\mathrm{cholesterol}-243)_{+}^{3} \\ +1.69\!\times\!10^{-8 }(\mathrm{cholesterol}-319)_{+}^{3} ]\\ +\mathrm{age}'[0.00341 \mathrm{cholesterol}-4.02\!\times\!10^{-7}(\mathrm{cholesterol}-160)_{+}^{3} \\ +9.71\!\times\!10^{-7 }(\mathrm{cholesterol}-208)_{+}^{3}-5.79\!\times\!10^{-7}(\mathrm{cholesterol}-243)_{+}^{3} \\ +8.79\!\times\!10^{-9 }(\mathrm{cholesterol}-319)_{+}^{3} ]\\ +\mathrm{age}''[-0.029 \mathrm{cholesterol}+3.04\!\times\!10^{-6 }(\mathrm{cholesterol}-160)_{+}^{3} \\ -7.34\!\times\!10^{-6}(\mathrm{cholesterol}-208)_{+}^{3}+4.36\!\times\!10^{-6 }(\mathrm{cholesterol}-243)_{+}^{3} \\ -5.82\!\times\!10^{-8}(\mathrm{cholesterol}-319)_{+}^{3} ] \end{array}\]

Code

print(anova(f), caption='Cubic spline surface')

Cubic spline surface
	χ²	d.f.	P
age (Factor+Higher Order Factors)	165.23	15	<0.0001
All Interactions	37.32	12	0.0002
Nonlinear (Factor+Higher Order Factors)	21.01	10	0.0210
sex (Factor+Higher Order Factors)	343.67	4	<0.0001
All Interactions	23.31	3	<0.0001
cholesterol (Factor+Higher Order Factors)	97.50	12	<0.0001
All Interactions	12.95	9	0.1649
Nonlinear (Factor+Higher Order Factors)	13.62	8	0.0923
age × sex (Factor+Higher Order Factors)	23.31	3	<0.0001
Nonlinear	13.37	2	0.0013
Nonlinear Interaction : f(A,B) vs. AB	13.37	2	0.0013
age × cholesterol (Factor+Higher Order Factors)	12.95	9	0.1649
Nonlinear	7.27	8	0.5078
Nonlinear Interaction : f(A,B) vs. AB	7.27	8	0.5078
f(A,B) vs. Af(B) + Bg(A)	5.41	4	0.2480
Nonlinear Interaction in age vs. Af(B)	6.44	6	0.3753
Nonlinear Interaction in cholesterol vs. Bg(A)	6.27	6	0.3931
TOTAL NONLINEAR	29.22	14	0.0097
TOTAL INTERACTION	37.32	12	0.0002
TOTAL NONLINEAR + INTERACTION	45.41	16	0.0001
TOTAL	450.88	19	<0.0001

Code

bplot(Predict(f, cholesterol, age, np=40), perim=perim,
      lfun=wireframe, zlim=zl, adj.subtitle=FALSE)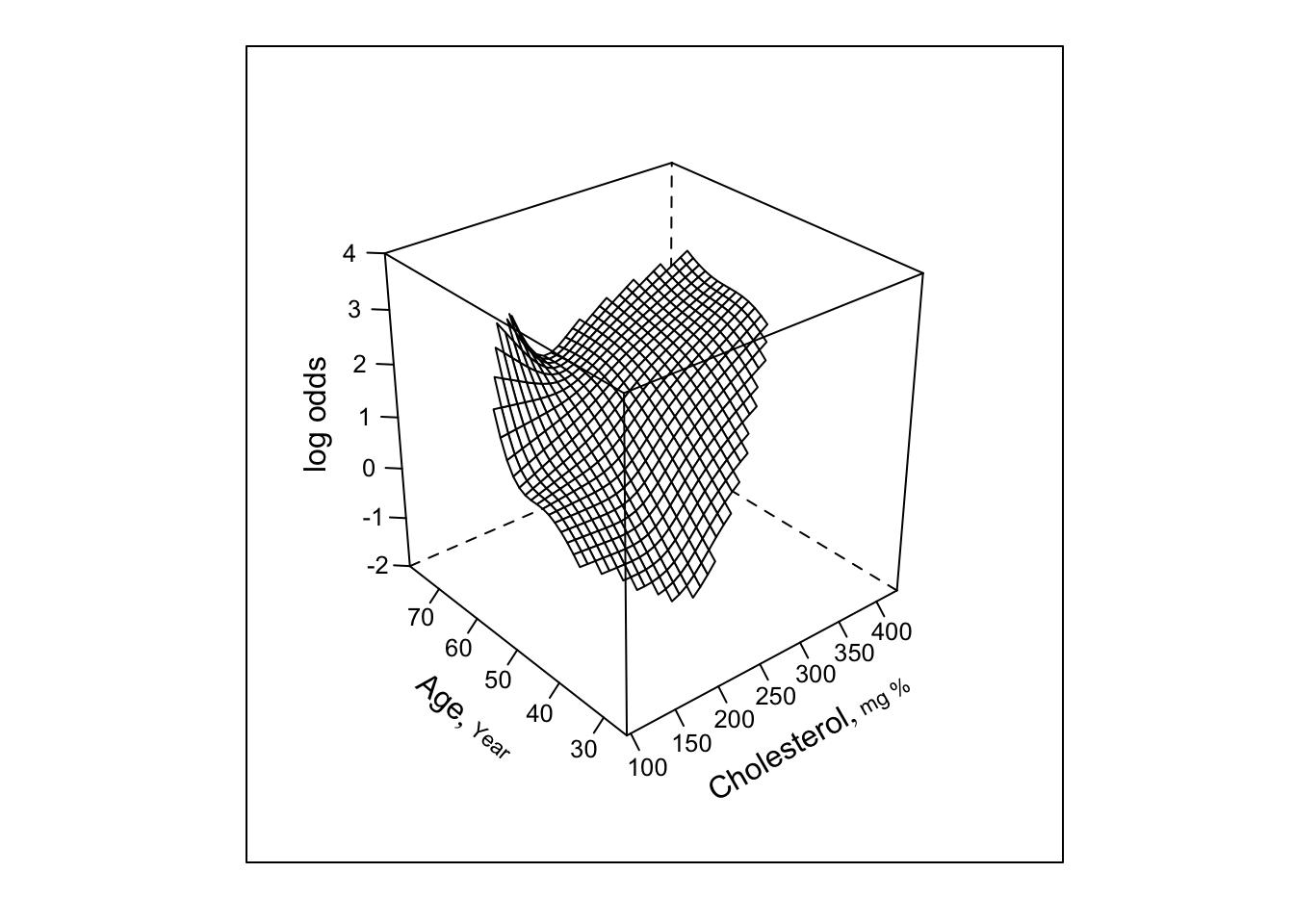

Figure 10.12: Restricted cubic spline surface in two variables, each with \(k=4\) knots

Now restrict surface by excluding doubly nonlinear terms

Code

f <- lrm(sigdz ~ sex*rcs(age,4) + rcs(cholesterol,4) +
         rcs(age,4) %ia% rcs(cholesterol,4), data=acath)
ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -7.2\\ +2.96[\mathrm{female}]\\+ 0.164 \mathrm{age}+7.23\!\times\!10^{-5 }(\mathrm{age}-36)_{+}^{3}-0.000106(\mathrm{age}-48)_{+}^{3} \\ -1.63\!\times\!10^{-5}(\mathrm{age}-56)_{+}^{3}+4.99\!\times\!10^{-5 }(\mathrm{age}-68)_{+}^{3} \\+ 0.0148 \mathrm{cholesterol}+1.21\!\times\!10^{-6 }(\mathrm{cholesterol}-160)_{+}^{3} \\ -5.5\!\times\!10^{-6 }(\mathrm{cholesterol}-208)_{+}^{3}+5.5\!\times\!10^{-6 }(\mathrm{cholesterol}-243)_{+}^{3} \\ -1.21\!\times\!10^{-6}(\mathrm{cholesterol}-319)_{+}^{3} \\ +\mathrm{age}[-0.00029 \mathrm{cholesterol}+9.28\!\times\!10^{-9 }(\mathrm{cholesterol}-160)_{+}^{3} \\ +1.7\!\times\!10^{-8 }(\mathrm{cholesterol}-208)_{+}^{3}-4.43\!\times\!10^{-8}(\mathrm{cholesterol}-243)_{+}^{3} \\ +1.79\!\times\!10^{-8 }(\mathrm{cholesterol}-319)_{+}^{3} ]\\ +\mathrm{cholesterol}[2.3\!\times\!10^{-7 }(\mathrm{age}-36)_{+}^{3}+4.21\!\times\!10^{-7 }(\mathrm{age}-48)_{+}^{3} \\ -1.31\!\times\!10^{-6}(\mathrm{age}-56)_{+}^{3}+6.64\!\times\!10^{-7 }(\mathrm{age}-68)_{+}^{3} ]\\ +[\mathrm{female}][-0.111 \mathrm{age}+8.03\!\times\!10^{-5}(\mathrm{age}-36)_{+}^{3}+0.000135(\mathrm{age}-48)_{+}^{3} \\ -0.00044(\mathrm{age}-56)_{+}^{3}+0.000224(\mathrm{age}-68)_{+}^{3} ] \end{array}\]

Code

print(anova(f),
      caption='Singly nonlinear cubic spline surface')

Singly nonlinear cubic spline surface
	χ²	d.f.	P
sex (Factor+Higher Order Factors)	343.42	4	<0.0001
All Interactions	24.05	3	<0.0001
age (Factor+Higher Order Factors)	169.35	11	<0.0001
All Interactions	34.80	8	<0.0001
Nonlinear (Factor+Higher Order Factors)	16.55	6	0.0111
cholesterol (Factor+Higher Order Factors)	93.62	8	<0.0001
All Interactions	10.83	5	0.0548
Nonlinear (Factor+Higher Order Factors)	10.87	4	0.0281
age × cholesterol (Factor+Higher Order Factors)	10.83	5	0.0548
Nonlinear	3.12	4	0.5372
Nonlinear Interaction : f(A,B) vs. AB	3.12	4	0.5372
Nonlinear Interaction in age vs. Af(B)	1.60	2	0.4496
Nonlinear Interaction in cholesterol vs. Bg(A)	1.64	2	0.4400
sex × age (Factor+Higher Order Factors)	24.05	3	<0.0001
Nonlinear	13.58	2	0.0011
Nonlinear Interaction : f(A,B) vs. AB	13.58	2	0.0011
TOTAL NONLINEAR	27.89	10	0.0019
TOTAL INTERACTION	34.80	8	<0.0001
TOTAL NONLINEAR + INTERACTION	45.45	12	<0.0001
TOTAL	453.10	15	<0.0001

Code

bplot(Predict(f, cholesterol, age, np=40), perim=perim,
      lfun=wireframe, zlim=zl, adj.subtitle=FALSE)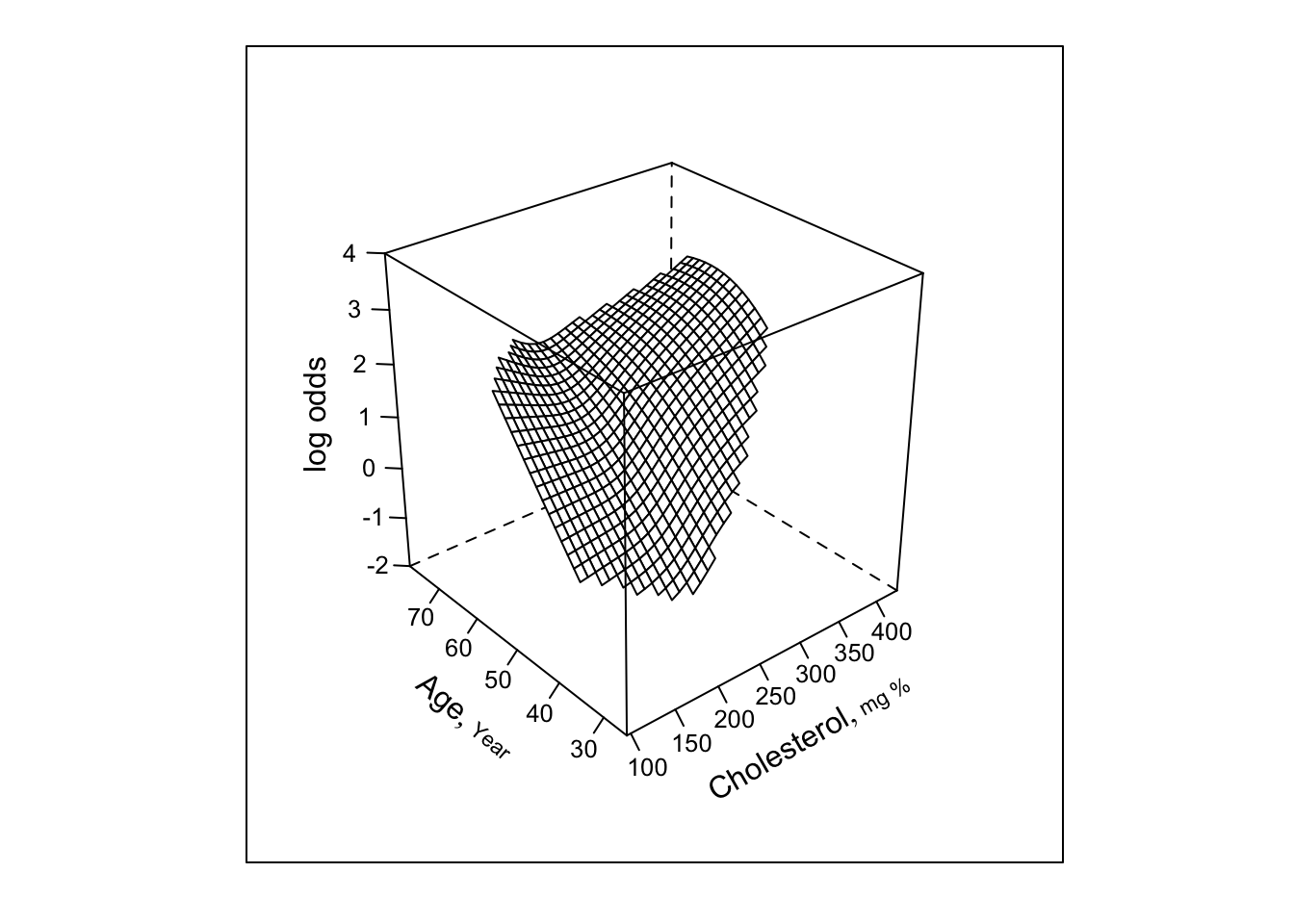

Figure 10.13: Restricted cubic spline fit with age \(\times\) spline(cholesterol) and cholesterol \(\times\) spline(age)

Finally restrict the interaction to be a simple product

Code

f <- lrm(sigdz ~ rcs(age,4)*sex + rcs(cholesterol,4) +
         age %ia% cholesterol, data=acath)
ltx(f)

\[X\hat{\beta}=\]

\[\begin{array}{l} -7.36\\+ 0.182 \mathrm{age}-5.18\!\times\!10^{-5}(\mathrm{age}-36)_{+}^{3}+8.45\!\times\!10^{-5 }(\mathrm{age}-48)_{+}^{3} \\ -2.91\!\times\!10^{-6}(\mathrm{age}-56)_{+}^{3}-2.99\!\times\!10^{-5}(\mathrm{age}-68)_{+}^{3} \\ +2.8[\mathrm{female}]\\+ 0.0139 \mathrm{cholesterol}+1.76\!\times\!10^{-6 }(\mathrm{cholesterol}-160)_{+}^{3} \\ -4.88\!\times\!10^{-6}(\mathrm{cholesterol}-208)_{+}^{3}+3.45\!\times\!10^{-6 }(\mathrm{cholesterol}-243)_{+}^{3} \\ -3.26\!\times\!10^{-7}(\mathrm{cholesterol}-319)_{+}^{3} \\ -0.00034\:\mathrm{age}\:\times\:\mathrm{cholesterol}\\ +[\mathrm{female}][-0.107 \mathrm{age}+7.71\!\times\!10^{-5 }(\mathrm{age}-36)_{+}^{3}+0.000115 (\mathrm{age}-48)_{+}^{3} \\ -0.000398(\mathrm{age}-56)_{+}^{3}+0.000205 (\mathrm{age}-68)_{+}^{3} ] \end{array}\]

Code

print(anova(f), caption='Linear interaction surface')

Linear interaction surface
	χ²	d.f.	P
age (Factor+Higher Order Factors)	167.83	7	<0.0001
All Interactions	31.03	4	<0.0001
Nonlinear (Factor+Higher Order Factors)	14.58	4	0.0057
sex (Factor+Higher Order Factors)	345.88	4	<0.0001
All Interactions	22.30	3	<0.0001
cholesterol (Factor+Higher Order Factors)	89.37	4	<0.0001
All Interactions	7.99	1	0.0047
Nonlinear	10.65	2	0.0049
age × cholesterol (Factor+Higher Order Factors)	7.99	1	0.0047
age × sex (Factor+Higher Order Factors)	22.30	3	<0.0001
Nonlinear	12.06	2	0.0024
Nonlinear Interaction : f(A,B) vs. AB	12.06	2	0.0024
TOTAL NONLINEAR	25.72	6	0.0003
TOTAL INTERACTION	31.03	4	<0.0001
TOTAL NONLINEAR + INTERACTION	43.59	8	<0.0001
TOTAL	452.75	11	<0.0001

Code

bplot(Predict(f, cholesterol, age, np=40), perim=perim,
      lfun=wireframe, zlim=zl, adj.subtitle=FALSE)
f.linia <- f  # save linear interaction fit for later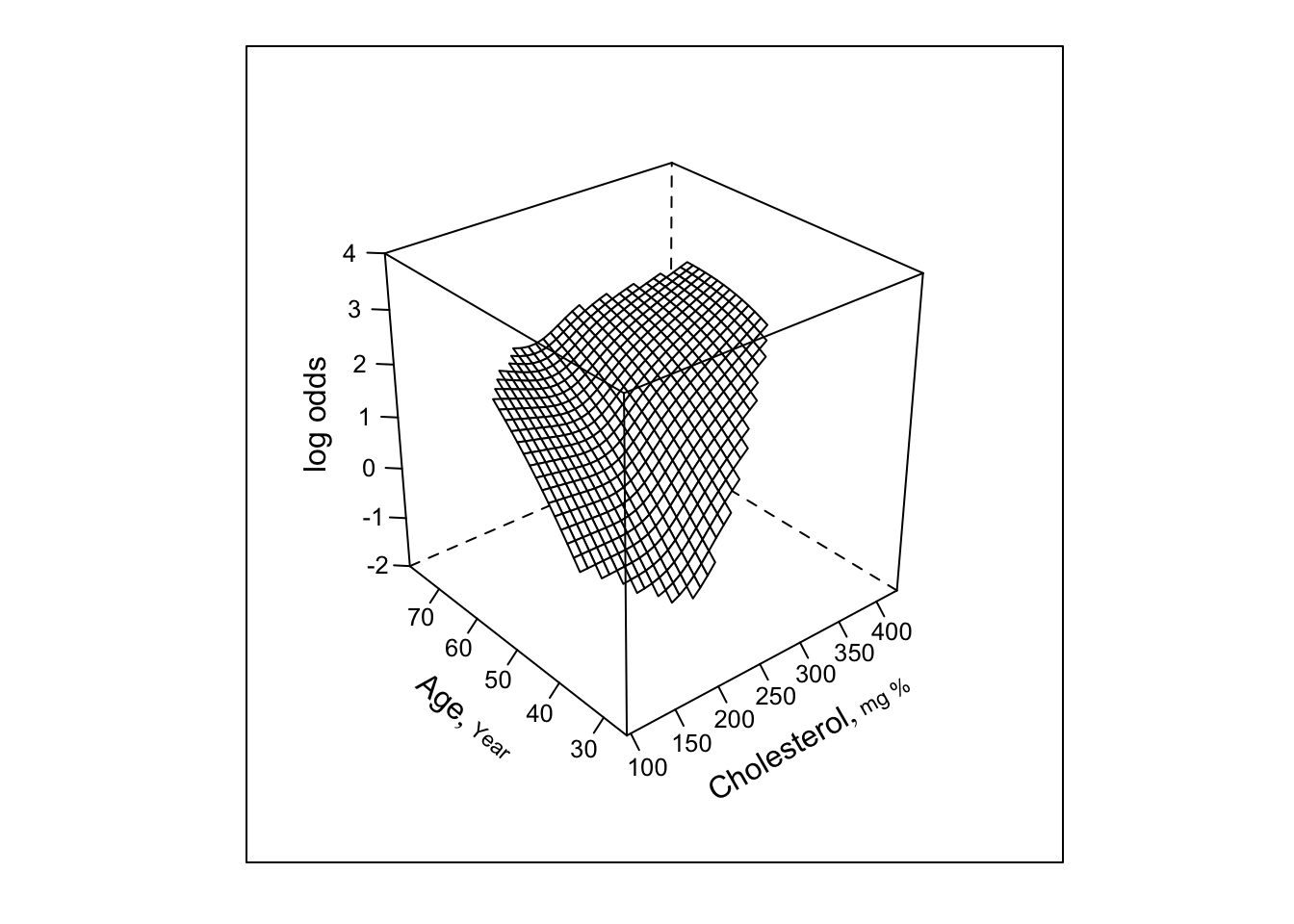

Figure 10.14: Spline fit with nonlinear effects of cholesterol and age and a simple product interaction

The Wald test for age \(\times\) cholesterol interaction yields \(\chi^{2}=7.99\) with 1 d.f., p=.005. * See how well this simple interaction model compares with initial model using 2 dummies for age * Request predictions to be made at mean age within tertiles

Code

# Make estimates of cholesterol effects for mean age in
# tertiles corresponding to initial analysis
mean.age <-
  with(acath,
       as.vector(tapply(age, age.tertile, mean, na.rm=TRUE)))
mean.age <- unique(mb(acath$age, g=3))
ggplot(Predict(f, cholesterol, age=round(mean.age, 2),
             sex="male"),
     adj.subtitle=FALSE, ylim=yl) #3 curves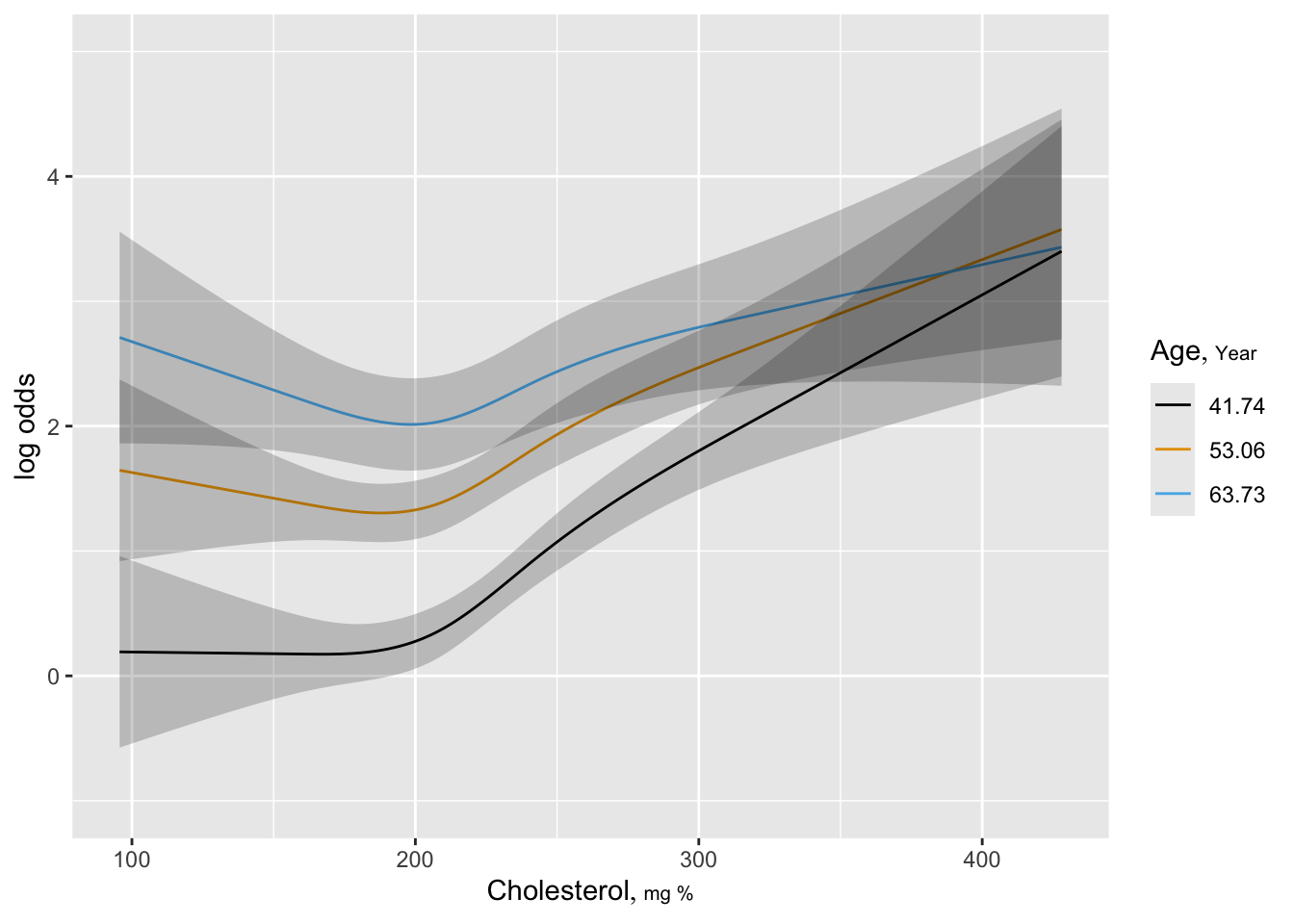

Figure 10.15: Predictions from linear interaction model with mean age in tertiles indicated.

Using residuals for “duration of symptoms” example

Code

spar(mfrow=c(1,2), ps=10)
f <- lrm(tvdlm ~ cad.dur, data=d, x=TRUE, y=TRUE)
resid(f, "partial", pl="loess", xlim=c(0,250), ylim=c(-3,3))
scat1d(d$cad.dur)
log.cad.dur <- log10(d$cad.dur + 1)
f <- lrm(tvdlm ~ log.cad.dur, data=d, x=TRUE, y=TRUE)
resid(f, "partial", pl="loess", ylim=c(-3,3))
scat1d(log.cad.dur)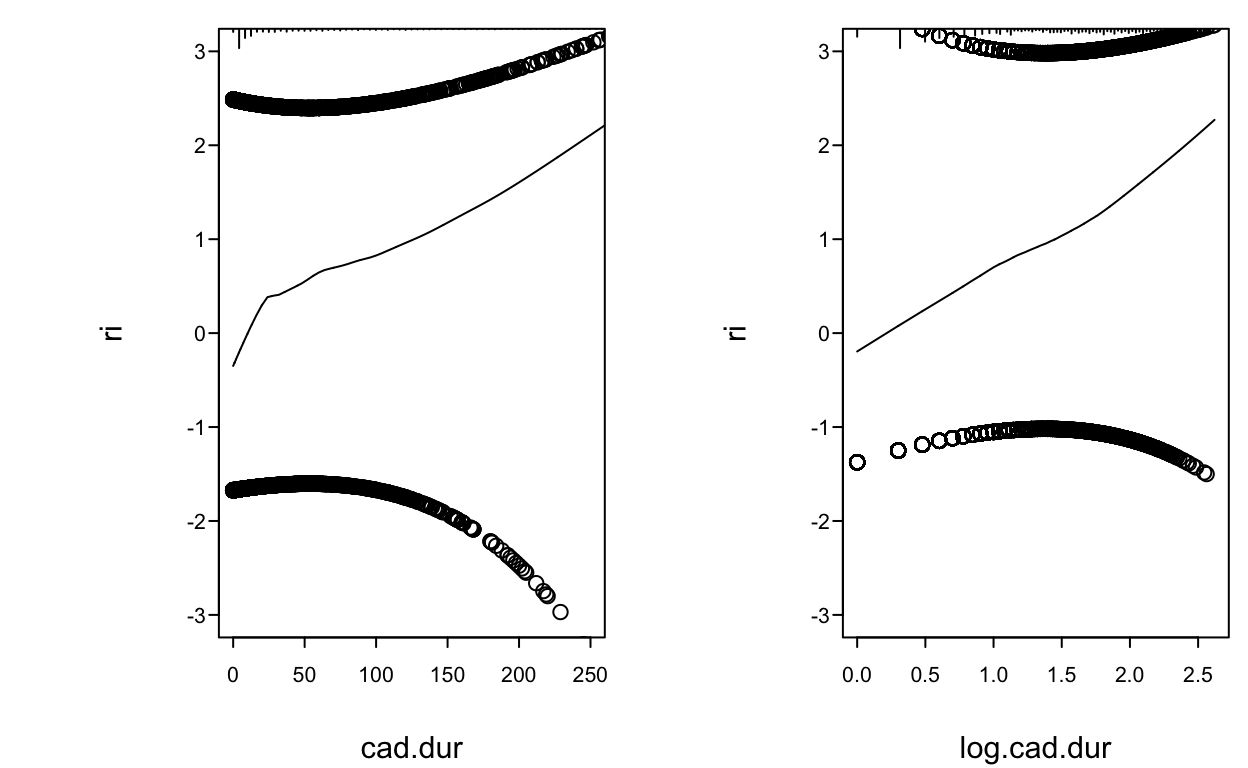

Figure 10.16: Partial residuals for duration and \(\log_{10}\)(duration+1). Data density shown at top of each plot.

Relative merits of strat., nonparametric, splines for checking fit

Method	Choice Required	Assumes Additivity	Uses Ordering of \(X\)	Low Variance	Good Resolution on \(X\)
Stratification	Intervals
Smoother on \(X_{1}\) stratifying on \(X_{2}\)	Bandwidth		× (not on \(X_2\))	× (if min. strat.)	× (\(X_1\))
Smooth partial residual plot	Bandwidth	×	×	×	×
Spline model for all \(X\)x	Knots	×	×	×	×

Hosmer-Lemeshow test is a commonly used test of goodness-of-fit of a binary logistic model
Compares proportion of events with mean predicted probability within deciles of \(\hat{P}\)
- Arbitrary (number of groups, how to form groups)
- Low power (too many d.f.)
- Does not reveal the culprits
A new omnibus test based of SSE has more power and requires no grouping; still does not lead to corrective action.
Any omnibus test lacks power against specific alternatives such as nonlinearity or interaction

10.6 Collinearity

10.7 Overly Influential Observations

10.8 Quantifying Predictive Ability

Generalized Nagelkerke \(R^2\): equals ordinary \(R^2\) in normal case: \[ R^{2}_{\rm N} = \frac{1 - \exp(-{\rm LR}/n)}{1 - \exp(-L^{0}/n)}, \]
4 versions of Maddala-Cox-Snell \(R^2\): hbiostat.org/bib/r2.html
- Perhaps best: \(R^{2}_{p,m} = 1 - \exp(-({\rm LR} - p) / m)\)
- \(m\) is the effective sample size based on approximate variance of a log odds ratio in a proportional odds ordinal logistic model
- If \(Y\) has \(k\) distinct values with proportions \(p_{1}, p_{2}, \ldots, p_{k}\),
  \(m=n \times (1 - \sum_{i=1}^{k}p_{i}^{3})\)
- For binary \(Y\) with proportion \(Y=1\) of \(p\),
  \(m=n\times 3p(1-p)\)
With perfect prediction in the case where there are 50 \(X=0\) and 50 \(X=1\) with \(Y=X\), \(R^{2}_{N}=1, R^{2}_{n,0}=0.75, R^{2}_{m,0}=0.84\)
Brier score (calibration + discrimination): \[ B = \frac{1}{n} \sum_{i=1}^{n} (\hat{P}_{i} - Y_{i})^{2}, \]
\(c\) = “concordance probability” = ROC area
- Related to Wilcoxon-Mann-Whitney stat and Somers’ \(D_{xy}\) \[ D_{xy} = 2 (c-.5) . \]
- Good pure index of predictive discrimination for a single model
- Not useful for comparing two models (Cook, 2007; Pencina et al., 2008)⁴
“Coefficient of discrimination” (Tjur, 2009): average \(\hat{P}\) when \(Y=1\) minus average \(\hat{P}\) when \(Y=0\)
- Has many advantages. Tjur shows how it ties in with sum of squares–based \(R^{2}\) measures.
“Percent classified correctly” has lots of problems
- improper scoring rule; optimizing it will lead to incorrect model
- arbitrary, insensitive, uses a strange loss (utility function)

⁴ But see Pencina et al. (2012).

10.9 Validating the Fitted Model

Possible indexes (Austin & Steyerberg, 2019)
- Accuracy of \(\hat{P}\): calibration
  Plot \(\text{expit}(X_{new}\hat{\beta}_{old})\) against estimated \(\Pr(Y=1)\) on new data
- Discrimination: \(C\) or \(D_{xy}\)
- \(R^2\) or \(B\)
Use bootstrap to estimate calibration equation \[ P_{c} = \Pr(Y=1 | X\hat{\beta}) = \text{expit}(\gamma_{0} + \gamma_{1} X\hat{\beta}) \] \[ E_{max}(a,b) = \max_{a \leq \hat{P} \leq b} |\hat{P} - \hat{P}_{c}| , \]
Bootstrap validation of age-sex-response data, 150 samples
2 predictors forced into every model

Code

d  <- sex.age.response
dd <- datadist(d); options(datadist='dd')
f  <- lrm(response ~ sex + age, data=d, x=TRUE, y=TRUE)
set.seed(3)  # for reproducibility
v1  <- validate(f, B=150)
ap1 <- round(v1[,'index.orig'], 2)
bc1 <- round(v1[,'index.corrected'], 2)
print(v1,
      caption='Bootstrap Validation, 2 Predictors Without Stepdown',
      digits=2)

Bootstrap Validation, 2 Predictors Without Stepdown
Index	Original Sample	Training Sample	Test Sample	Optimism	Corrected Index	Successful Resamples
D_xy	0.7	0.7	0.67	0.03	0.66	150
R²	0.45	0.48	0.43	0.05	0.4	150
Intercept	0	0	0.04	-0.04	0.04	150
Slope	1	1	0.92	0.08	0.92	150
E_max	0	0	0.03	0.03	0.03	150
D	0.39	0.43	0.36	0.07	0.32	150
U	-0.05	-0.05	0.02	-0.07	0.02	150
Q	0.44	0.48	0.34	0.14	0.3	150
B	0.16	0.15	0.18	-0.03	0.19	150
g	2.1	2.38	1.97	0.41	1.7	150
g_p	0.35	0.35	0.34	0.01	0.34	150

Allow for step-down at each re-sample
Use individual tests at \(\alpha=0.10\)
Both age and sex selected in 137 of 150, neither in 3 samples

Code

v2 <- validate(f, B=150, bw=TRUE,
               rule='p', sls=.1, type='individual')


        Backwards Step-down - Original Model

No Factors Deleted

Factors in Final Model

[1] sex age

Code

ap2 <- round(v2[,'index.orig'], 2)
bc2 <- round(v2[,'index.corrected'], 2)
print(v2,
      caption='Bootstrap Validation, 2 Predictors with Stepdown',
      digits=2, B=15)

Bootstrap Validation, 2 Predictors with Stepdown
Index	Original Sample	Training Sample	Test Sample	Optimism	Corrected Index	Successful Resamples
D_xy	0.7	0.71	0.65	0.07	0.63	150
R²	0.45	0.5	0.41	0.09	0.36	150
Intercept	0	0	0.01	-0.01	0.01	150
Slope	1	1	0.83	0.17	0.83	150
E_max	0	0	0.04	0.04	0.04	150
D	0.39	0.46	0.35	0.11	0.28	150
U	-0.05	-0.05	0.05	-0.1	0.05	150
Q	0.44	0.51	0.29	0.21	0.22	150
B	0.16	0.14	0.18	-0.04	0.2	150
g	2.1	2.6	1.9	0.7	1.4	150
g_p	0.35	0.35	0.33	0.02	0.33	150

Factors Retained in Backwards Elimination First 15 Resamples
sex	age
⚬	⚬
⚬	⚬
⚬	⚬
⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬

Frequencies of Numbers of Factors Retained
0	1	2
1	11	138

Try adding 5 noise candidate variables

Code

set.seed(133)
n  <- nrow(d)
x1 <- runif(n)
x2 <- runif(n)
x3 <- runif(n)
x4 <- runif(n)
x5 <- runif(n)
f  <- lrm(response ~ age + sex + x1 + x2 + x3 + x4 + x5,
          data=d, x=TRUE, y=TRUE)
v3 <- validate(f, B=150, bw=TRUE,
               rule='p', sls=.1, type='individual')


        Backwards Step-down - Original Model

 Deleted Chi-Sq d.f. P      Residual d.f. P      AIC  
 x1      0.01   1    0.9261 0.01     1    0.9261 -1.99
 x5      0.53   1    0.4650 0.54     2    0.7624 -3.46
 x4      0.74   1    0.3902 1.28     3    0.7337 -4.72
 x2      1.03   1    0.3113 2.31     4    0.6796 -5.69
 x3      0.94   1    0.3333 3.24     5    0.6627 -6.76

Approximate Estimates after Deleting Factors

             Coef    S.E. Wald Z        P
Intercept -8.8187 3.76406 -2.343 0.019136
age        0.1415 0.06469  2.188 0.028698
sex=male   3.1059 1.18103  2.630 0.008544

Factors in Final Model

[1] age sex

Divergence or singularity in 14 samples

Code

ap3 <- round(v3[,'index.orig'], 2)
bc3 <- round(v3[,'index.corrected'], 2)
k <- attr(v3, 'kept')
# Compute number of x1-x5 selected
nx <- apply(k[,3:7], 1, sum)
# Get selections of age and sex
v <- colnames(k)
as <- apply(k[,1:2], 1,
            function(x) paste(v[1:2][x], collapse=', '))

Code

kabl(table(paste(as, ' ', nx, 'Xs')))

0 Xs	1 Xs	age, sex 0 Xs	age, sex 1 Xs	age, sex 2 Xs	age, sex 3 Xs	sex 0 Xs	sex 1 Xs	sex 2 Xs
50	4	30	26	8	5	9	3	1

Code

print(v3,
      caption='Bootstrap Validation with 5 Noise Variables and Stepdown',
      digits=2, B=15)

Bootstrap Validation with 5 Noise Variables and Stepdown
Index	Original Sample	Training Sample	Test Sample	Optimism	Corrected Index	Successful Resamples
D_xy	0.7	0.47	0.38	0.09	0.61	136
R²	0.45	0.34	0.23	0.11	0.34	136
Intercept	0	0	0.04	-0.04	0.04	136
Slope	1	1	0.77	0.23	0.77	136
E_max	0	0	0.07	0.07	0.07	136
D	0.39	0.31	0.18	0.13	0.26	136
U	-0.05	-0.05	0.06	-0.11	0.06	136
Q	0.44	0.36	0.12	0.24	0.2	136
B	0.16	0.18	0.21	-0.04	0.2	136
g	2.1	1.81	1.06	0.75	1.35	136
g_p	0.35	0.24	0.19	0.04	0.31	136

Factors Retained in Backwards Elimination First 15 Resamples
age	sex	x1	x2	x3	x4	x5
⚬	⚬
⚬	⚬

	⚬
⚬	⚬				⚬	⚬
⚬	⚬		⚬
⚬	⚬
⚬	⚬	⚬			⚬	⚬
	⚬
⚬	⚬	⚬


⚬	⚬		⚬

Frequencies of Numbers of Factors Retained
0	1	2	3	4	5
50	13	33	27	8	5

Repeat but force age and sex to be in all models

Code

v4 <- validate(f, B=150, bw=TRUE, rule='p', sls=.1,
               type='individual', force=1:2)


        Backwards Step-down - Original Model

Parameters forced into all models:
 age, sex=male 

 Deleted Chi-Sq d.f. P      Residual d.f. P      AIC  
 x1      0.01   1    0.9261 0.01     1    0.9261 -1.99
 x5      0.53   1    0.4650 0.54     2    0.7624 -3.46
 x4      0.74   1    0.3902 1.28     3    0.7337 -4.72
 x2      1.03   1    0.3113 2.31     4    0.6796 -5.69
 x3      0.94   1    0.3333 3.24     5    0.6627 -6.76

Approximate Estimates after Deleting Factors

             Coef    S.E. Wald Z        P
Intercept -8.8187 3.76406 -2.343 0.019136
age        0.1415 0.06469  2.188 0.028698
sex=male   3.1059 1.18103  2.630 0.008544

Factors in Final Model

[1] age sex

Divergence or singularity in 20 samples

Code

ap4 <- round(v4[,'index.orig'], 2)
bc4 <- round(v4[,'index.corrected'], 2)

Code

print(v4,
      caption='Bootstrap Validation with 5 Noise Variables and Stepdown, Forced Inclusion of age and sex',
      digits=2, B=15)

Bootstrap Validation with 5 Noise Variables and Stepdown, Forced Inclusion of age and sex
Index	Original Sample	Training Sample	Test Sample	Optimism	Corrected Index	Successful Resamples
D_xy	0.7	0.76	0.66	0.1	0.6	130
R²	0.45	0.54	0.41	0.12	0.33	130
Intercept	0	0	0.06	-0.06	0.06	130
Slope	1	1	0.76	0.24	0.76	130
E_max	0	0	0.07	0.07	0.07	130
D	0.39	0.5	0.35	0.15	0.24	130
U	-0.05	-0.05	0.08	-0.13	0.08	130
Q	0.44	0.55	0.27	0.28	0.16	130
B	0.16	0.14	0.18	-0.04	0.21	130
g	2.1	2.75	1.89	0.86	1.25	130
g_p	0.35	0.37	0.33	0.04	0.31	130

Factors Retained in Backwards Elimination First 15 Resamples
age	sex	x1	x2	x3	x4	x5
⚬	⚬
⚬	⚬
⚬	⚬			⚬
⚬	⚬
⚬	⚬		⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬
⚬	⚬					⚬
⚬	⚬		⚬
⚬	⚬

Frequencies of Numbers of Factors Retained
2	3	4	5	6
88	29	10	1	2

10.10 Describing the Fitted Model

Code

s <- summary(f.linia)
s

Effects Response: `sigdz`
	Low	High	Δ	Effect	S.E.	Lower 0.95	Upper 0.95
age	46	59	13	0.90630	0.1838	0.54600	1.2670
Odds Ratio	46	59	13	2.47500		1.72600	3.5490
cholesterol	196	259	63	0.75480	0.1364	0.48740	1.0220
Odds Ratio	196	259	63	2.12700		1.62800	2.7790
sex --- female:male	1	2		-2.43000	0.1484	-2.72100	-2.1390
Odds Ratio	1	2		0.08806		0.06584	0.1178

Code

plot(s)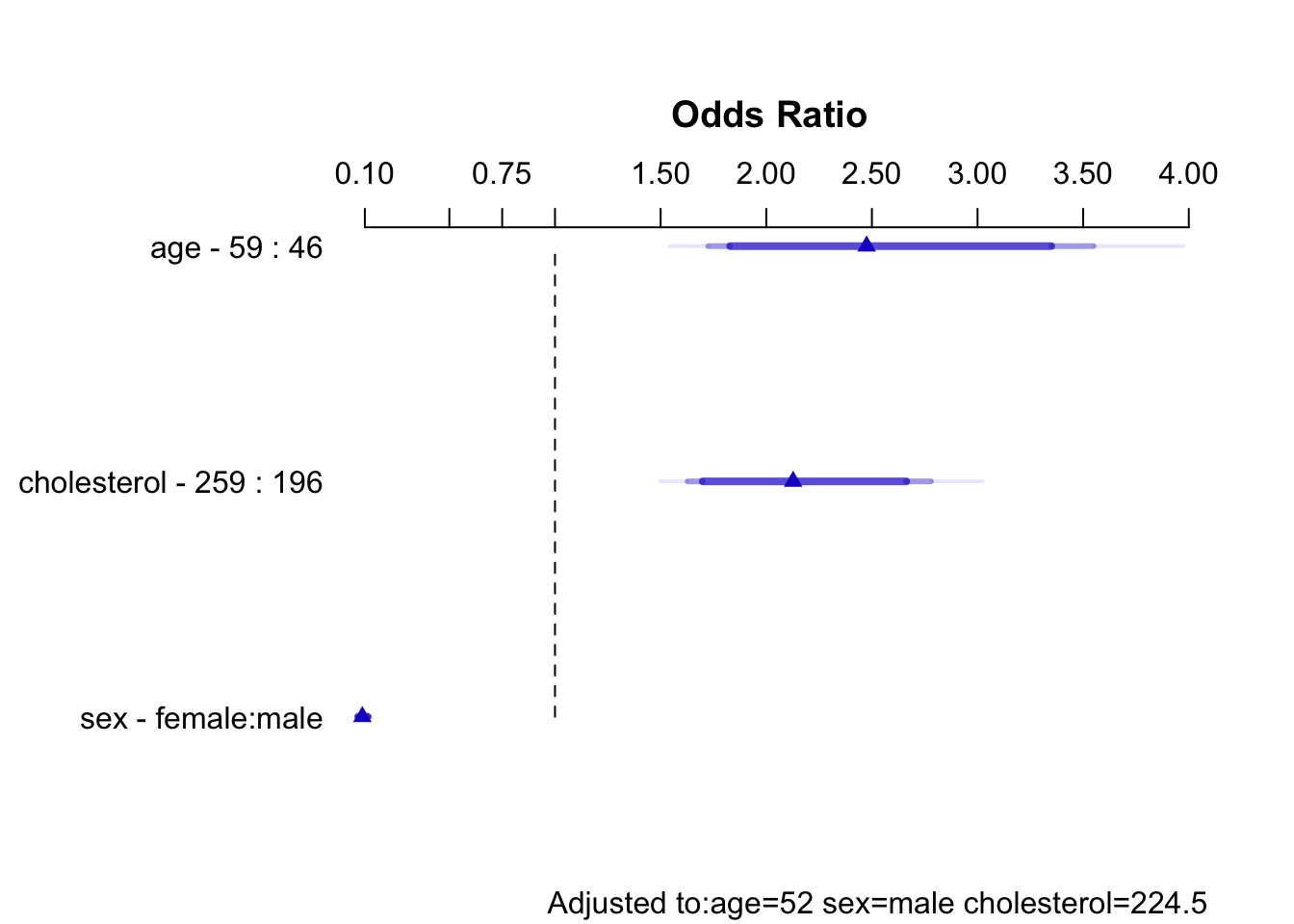

Figure 10.17: Odds ratios and confidence bars, using quartiles of age and cholesterol for assessing their effects on the odds of coronary disease.

Figure 10.18: Linear spline fit for probability of bacterial vs. viral meningitis as a function of age at onset (Spanos et al., 1989). Points are simple proportions by age quantile groups.

Figure 10.19: (A) Relationship between myocardium at risk and ventricular fibrillation, based on the individual best fit equations for animals anesthetized with pentobarbital and \(\alpha\)-chloralose. The amount of myocardium at risk at which 0.5 of the animals are expected to fibrillate \((\text{MAR}_{50})\) is shown for each anesthetic group. (B) Relationship between myocardium at risk and ventricular fibrillation, based on equations derived from the single slope estimate. Note that the \(\text{MAR}_{50}\) describes the overall relationship between myocardium at risk and outcome when either the individual best fit slope or the single slope estimate is used. The shift of the curve to the right during \(\alpha\)-chloralose anesthesia is well described by the shift in \(\text{MAR}_{50}\). Test for interaction had P=0.10 (Wenger et al., 1984). Reprinted by permission, NRC Research Press.

Figure 10.20: A nomogram for estimating the likelihood of significant coronary artery disease (CAD) in women. ECG = electrocardiographic; MI = myocardial infarction (Pryor et al., 1983). Reprinted from American Journal of Medicine, Vol 75, Pryor DB et al., “Estimating the likelihood of significant coronary artery disease”, p. 778, Copyright 1983, with permission from Excerpta Medica, Inc.

Figure 10.21: Nomogram for estimating probability of bacterial (ABM) vs. viral (AVM) meningitis. Step 1, place ruler on reading lines for patient’s age and month of presentation and mark intersection with line A; step 2, place ruler on values for glucose ratio and total polymorphonuclear leukocyte (PMN) count in cerebro-spinal fluid and mark intersection with line B; step 3, use ruler to join marks on lines A and B, then read off the probability of ABM vs. AVM (Spanos et al., 1989).

Code

#|label: fig-lrm-iacholxage-3-nomogram
# Draw a nomogram that shows examples of confidence intervals
nom <- nomogram(f.linia, cholesterol=seq(150, 400, by=50),
                interact=list(age=seq(30, 70, by=10)),
                lp.at=seq(-2, 3.5, by=.5),
                conf.int=TRUE, conf.lp="all",
                fun=function(x)1/(1+exp(-x)),  # or plogis
                funlabel="Probability of CAD",
                fun.at=c(seq(.1, .9, by=.1), .95, .99)
                )
plot(nom, col.grid = gray(c(0.8, 0.95)),
     varname.label=FALSE, ia.space=1, xfrac=.46, lmgp=.2)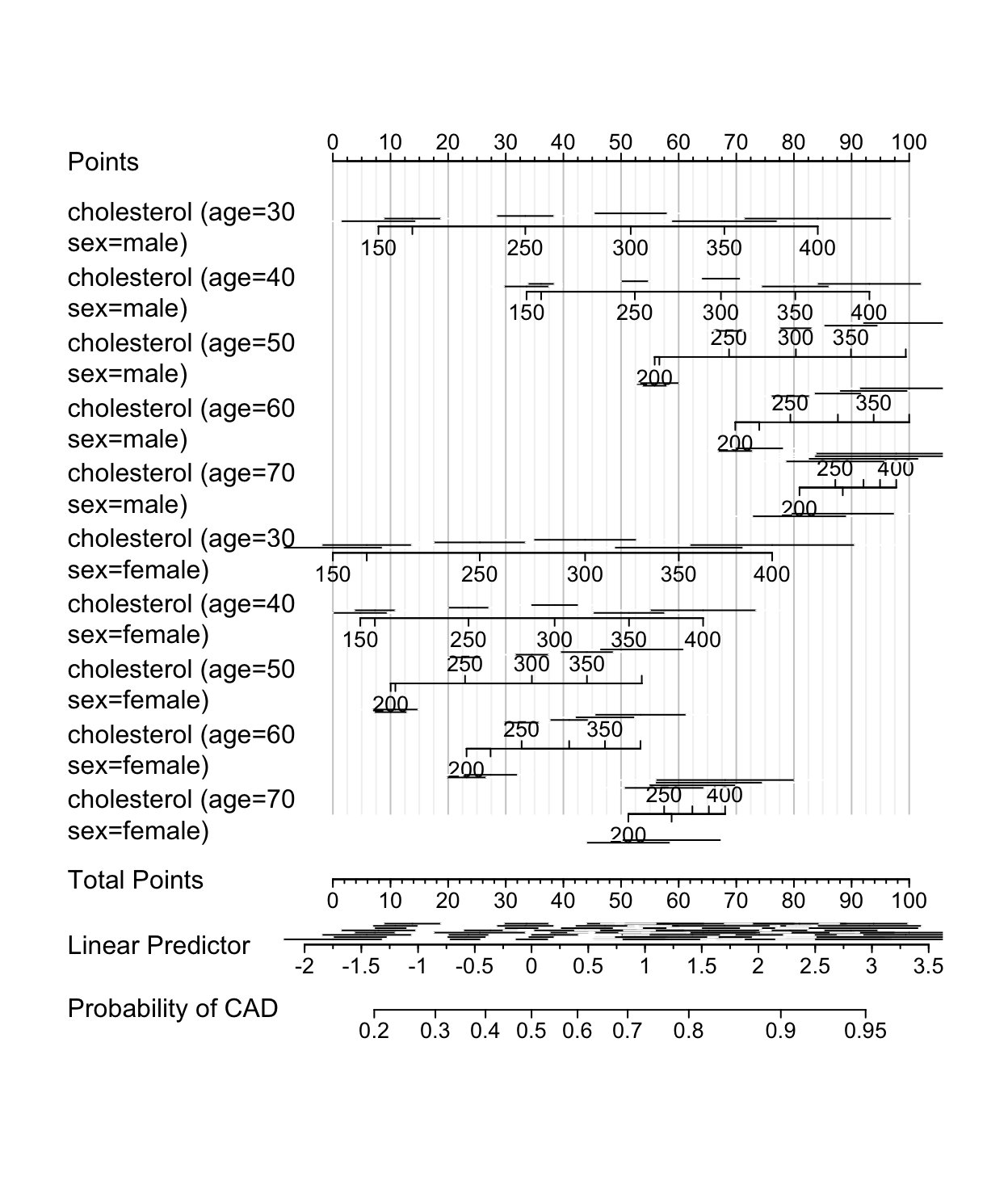

Nomogram relating age, sex, and cholesterol to the log odds and to the probability of significant coronary artery disease. Select one axis corresponding to sex and to age \(\in \{30,40,50,60,70\}\). There was linear interaction between age and sex and between age and cholesterol. 0.70 and 0.90 confidence intervals are shown (0.90 in gray). Note that for the `Linear Predictor` scale there are various lengths of confidence intervals near the same value of \(X\hat{\beta}\), demonstrating that the standard error of \(X\hat{\beta}\) depends on the individual \(X\) values. Also note that confidence intervals corresponding to smaller patient groups (e.g., females) are wider.

10.11 Bayesian Logistic Model Example

Re-analyze data in Section Section 10.1.3 using the R rmsb package. See hbiostat.org/doc/rms/lrm-brms.pdf for a parallel analysis using the brms package.

The rmsb package relies on the Stan Bayesian modeling system (Carpenter et al., 2017; Stan Development Team, 2020).

Code

dd <- datadist(sex.age.response)
options(datadist = 'dd')
require(rmsb)

# Frequentist model
flrm <- lrm(response ~ sex + age, data=sex.age.response)

# Bayesian model
# Distribute chains across all available cpu cores:
options(mc.cores=parallel::detectCores())

# Fit a model with all flat priors
set.seed(8)
ff <- blrm(response ~ sex + age, data=sex.age.response, iter=5000)
# Elapsed time 2.2s
kabl(round(rbind(MLE =coef(flrm), Mode  =coef(ff, 'mode'),
                 Mean=coef(ff),   Median=coef(ff, 'median')), 3))

	Intercept	sex=male	age
MLE	-9.843	3.490	0.158
Mode	-9.843	3.490	0.158
Mean	-11.393	3.979	0.183
Median	-11.071	3.883	0.179

The frequentist model was fitted using lrm and the Bayesian model is fitted using the rmsb blrm function. For the Bayesian model, the intercept prior is non-informative (iprior=1), and Gaussian priors with SD=100 are used for the two slopes. Posterior modes from this fit are in close agreement with the maximum likelihood estimates (MLE) from the frequentist model fit.

For blrm a complication arises in specifying non-default priors for regression coefficients. This is due to the QR decomposition being used on the design matrix to remove MCMC sampling problems with collinearities. By default, priors correspond to the re-mixed, scaled, and centered covariates. To keep predictors in raw form (and risk some posterior sampling problems), use the keepsep argument as done below on both predictors. Then Gaussian priors are used. The age and sex parameters were given mean zero priors with standard deviations computed to achieve specified tail prior probabilities. Four MCMC chains with 5000 iterations were used with a warm-up of 2500 iterations each, resulting in 10000 retained draws from the posterior distribution.

Code

# Set priors
# Solve for SD such that sex effect has only a 0.025 chance of
# being above 5 (or being below -5)

s1 <- 5 / qnorm(0.975)

# Solve for SD such that 10-year age effect has only 0.025 chance
# of being above 20

s2 <- (20 / qnorm(0.975)) / 10   # divide by 10 since ratio on 10b scale

# Full model
set.seed(11)
f <- blrm(response ~ sex + age, data=sex.age.response,
          priorsd=c(s1, s2), iprior=1, keepsep='age|sex', iter=5000)
# Elapsed time 1.7s
f

Bayesian Logistic Model

Non-informative Priors for Intercepts

blrm(formula = response ~ sex + age, keepsep = "age|sex", data = sex.age.response, 
    priorsdppo = c(s1, s2), iprior = 1, iter = 5000)

	Mixed Calibration/ Discrimination Indexes	Discrimination Indexes	Rank Discrim. Indexes
Obs 40	LOO log L -23.06±4.16	g 2.37 [0.892, 3.848]	C 0.837 [0.821, 0.851]
0 20	LOO IC 46.12±8.33	g_p 0.354 [0.248, 0.453]	D_xy 0.673 [0.643, 0.702]
1 20	Effective p 3.57±0.98	EV 0.39 [0.193, 0.63]
Draws 10000	B 0.175 [0.162, 0.195]	v 4.795 [0.508, 11.27]
Chains 4		vp 0.097 [0.042, 0.153]
Time 0.9s
p 2

	Mode β	Mean β	Median β	S.E.	Lower	Upper	Pr(β>0)	Symmetry
Intercept	-9.8429	-11.3259	-11.0030	3.9967	-19.0773	-3.8178	0.0001	0.79
sex=male	3.4898	3.9646	3.8516	1.3097	1.4903	6.5303	1.0000	1.26
age	0.1581	0.1821	0.1772	0.0668	0.0587	0.3146	0.9993	1.24

MCMC sampling diagnostics are below. No apparent problems.

Code

stanDx(f)

Iterations: 5000 on each of 4 chains, with 10000 posterior distribution samples saved

For each parameter, n_eff is a crude measure of effective sample size
and Rhat is the potential scale reduction factor on split chains
(at convergence, Rhat=1)

          n_eff Rhat
Intercept  6833    1
sex=male   5885    1
age        5673    1

Code

stanDxplot(f)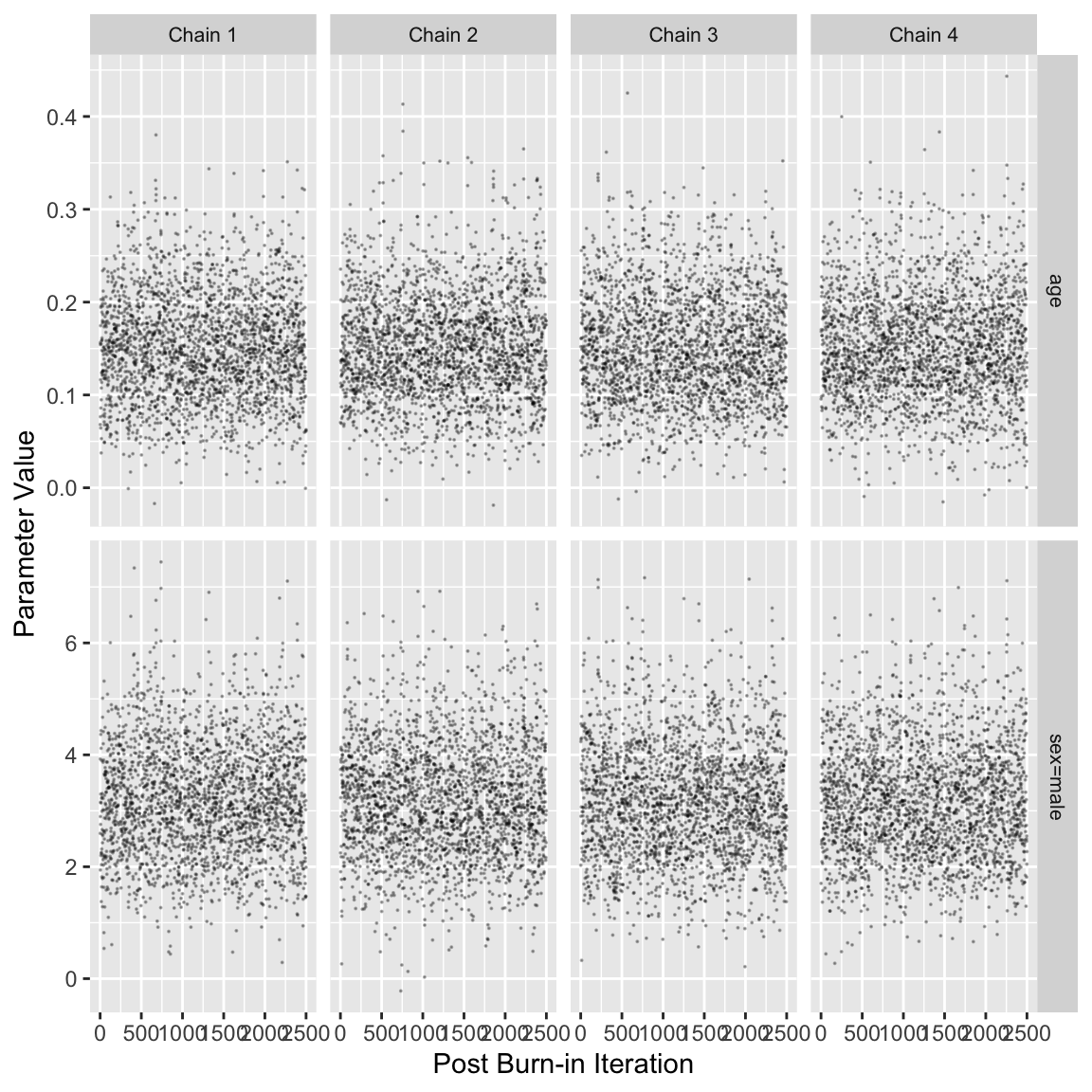

The model summaries for the frequentist and Bayesian models are shown below, with posterior means computed as Bayesian “point estimates.” The parameter estimates are similar for the two approaches. The frequentist 0.95 confidence interval for the age parameter is 0.037 - 0.279 while the Bayesian 0.95 credible interval is 0.047 - 0.263. Similarly, the 0.95 confidence interval for sex is 1.14 - 5.84 and the corresponding Bayesian 0.95 credible interval is 1.23 - 5.19. The results made sense in view of the use of skeptical priors when the sample size is small.

Code

# Frequentist model output
flrm

Logistic Regression Model

lrm(formula = response ~ sex + age, data = sex.age.response)

	Model Likelihood Ratio Test	Discrimination Indexes	Rank Discrim. Indexes
Obs 40	LR χ² 16.54	R² 0.451	C 0.849
0 20	d.f. 2	R²_2,40 0.305	D_xy 0.698
1 20	Pr(>χ²) 0.0003	R²_2,30 0.384	γ 0.703
max \|∂log L/∂β\| 7×10^-8		Brier 0.162	τ_a 0.358

	β	S.E.	Wald Z	Pr(>\|Z\|)
Intercept	-9.8429	3.6758	-2.68	0.0074
sex=male	3.4898	1.1992	2.91	0.0036
age	0.1581	0.0616	2.56	0.0103

Code

summary(flrm, age=20:21)

Effects Response: `response`
	Low	High	Δ	Effect	S.E.	Lower 0.95	Upper 0.95
age	20	21	1	0.1581	0.06164	0.03725	0.2789
Odds Ratio	20	21	1	1.1710		1.03800	1.3220
sex --- male:female	1	2		3.4900	1.19900	1.13900	5.8400
Odds Ratio	1	2		32.7800		3.12500	343.8000

Code

# Bayesian model output
summary(f, age=20:21)   # posterior means

Effects Response: `response`
	Low	High	Δ	Effect	S.E.	Lower 0.95	Upper 0.95
age	20	21	1	0.1821	0.0668	0.05875	0.3146
Odds Ratio	20	21	1	1.2000		1.06100	1.3700
sex --- male:female	1	2		3.9650	1.3100	1.49000	6.5300
Odds Ratio	1	2		52.7000		4.43800	685.6000

Code

summary(f, age=20:21, posterior.summary='median')   # post. medians

Effects Response: `response`
	Low	High	Δ	Effect	S.E.	Lower 0.95	Upper 0.95
age	20	21	1	0.1772	0.0668	0.05875	0.3146
Odds Ratio	20	21	1	1.1940		1.06100	1.3700
sex --- male:female	1	2		3.8520	1.3100	1.49000	6.5300
Odds Ratio	1	2		47.0700		4.43800	685.6000

Code

# Note that mean vs median doesn't affect HPD intervals, only pt estimates

The figure shows the posterior draws for the age and sex parameters as well as the trace of the 4 MCMC chains for each parameter and the bivariate posterior distribution. The posterior distributions of each parameter are roughly round shaped and the overlap between chains in the trace plots indicates good convergence. The bivariate density plot indicates moderate correlation between the age and sex parameters.

Create a 0.95 bivariate credible interval for the joint distribution of age and sex. Any number of intervals could be drawn, as any region that covers 0.95 of the posterior density could be accurately be called a 0.95 credible interval. Commonly used: maximum a-posteriori probability (MAP) interval, which seeks to find the region that holds 0.95 of the density, while also having the smallest area. In a 1-dimensional setting, this would translate into having the shortest interval length, and therefore the most precise estimate. The figure below shows the point estimate as well as the corresponding MAP interval.

Code

# display posterior densities for age and sex parameters
plot(f)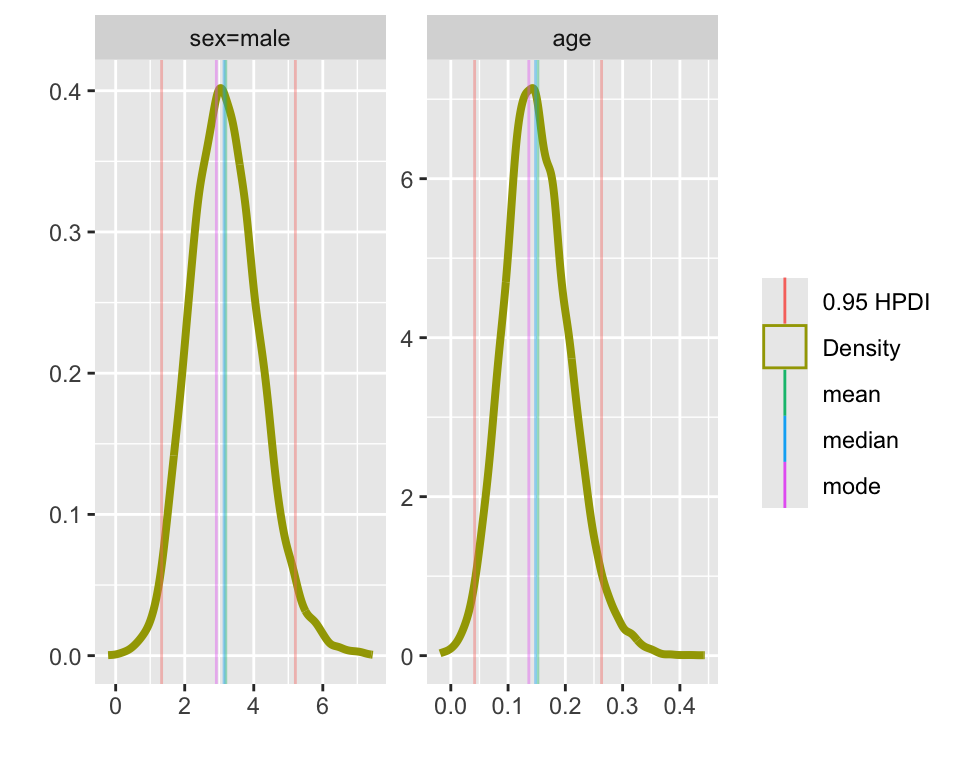

Code

plot(f, bivar=TRUE)   # MAP region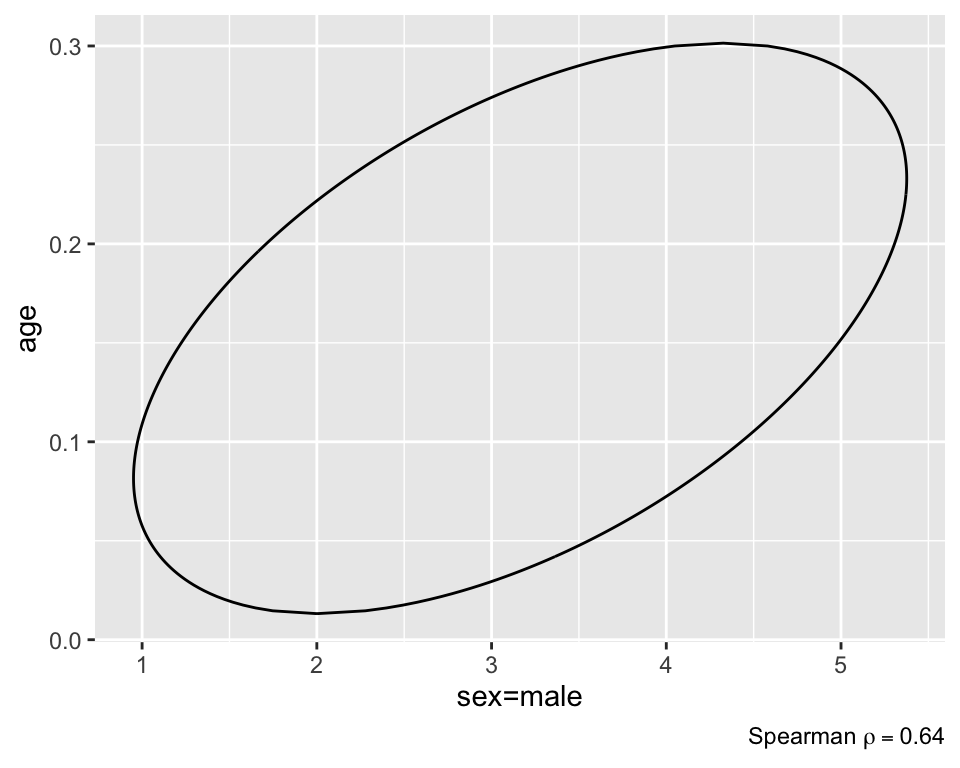

Code

plot(f, bivar=TRUE, bivarmethod='kernel')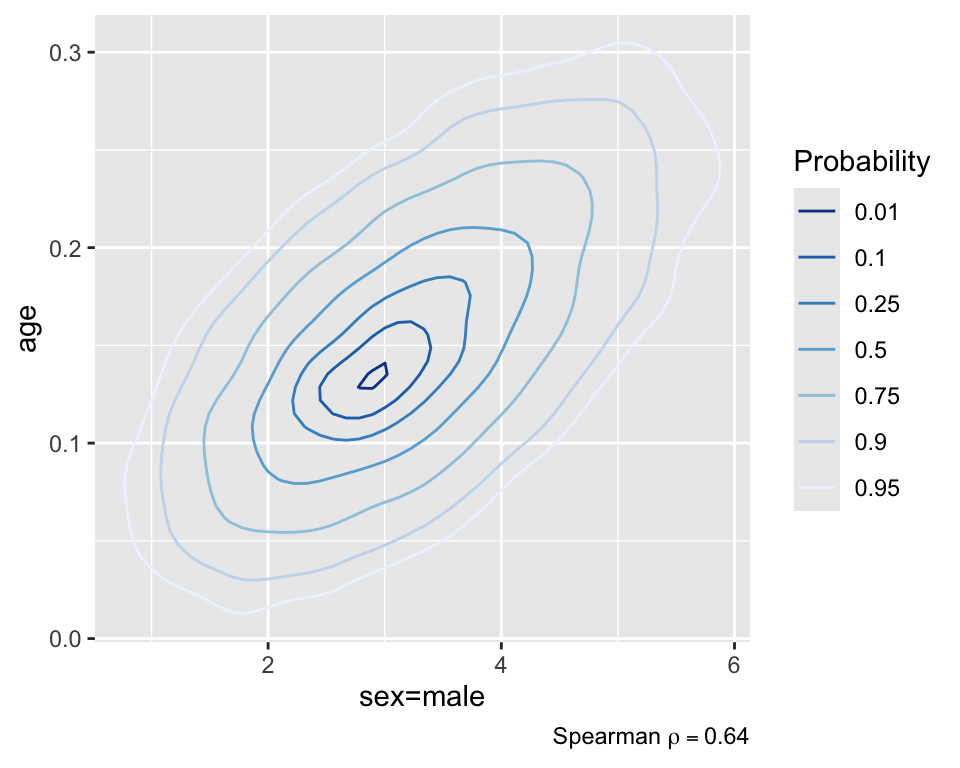

In the above figure, the point estimate does not appear quite at the point of highest density. This is because blrm estimates (by default) the posterior mean, rather than the posterior mode. You have the full posterior density, so you can calculate whatever you’d like if you don’t want the mean.

A plot of the partial effects on the probability scale from the Bayesian model reveals the same pattern as Figure 10.3 .

Code

# Partial effects plot
ggplot(Predict(f, age, sex, fun=plogis, funint=FALSE), ylab='P(Y=1)')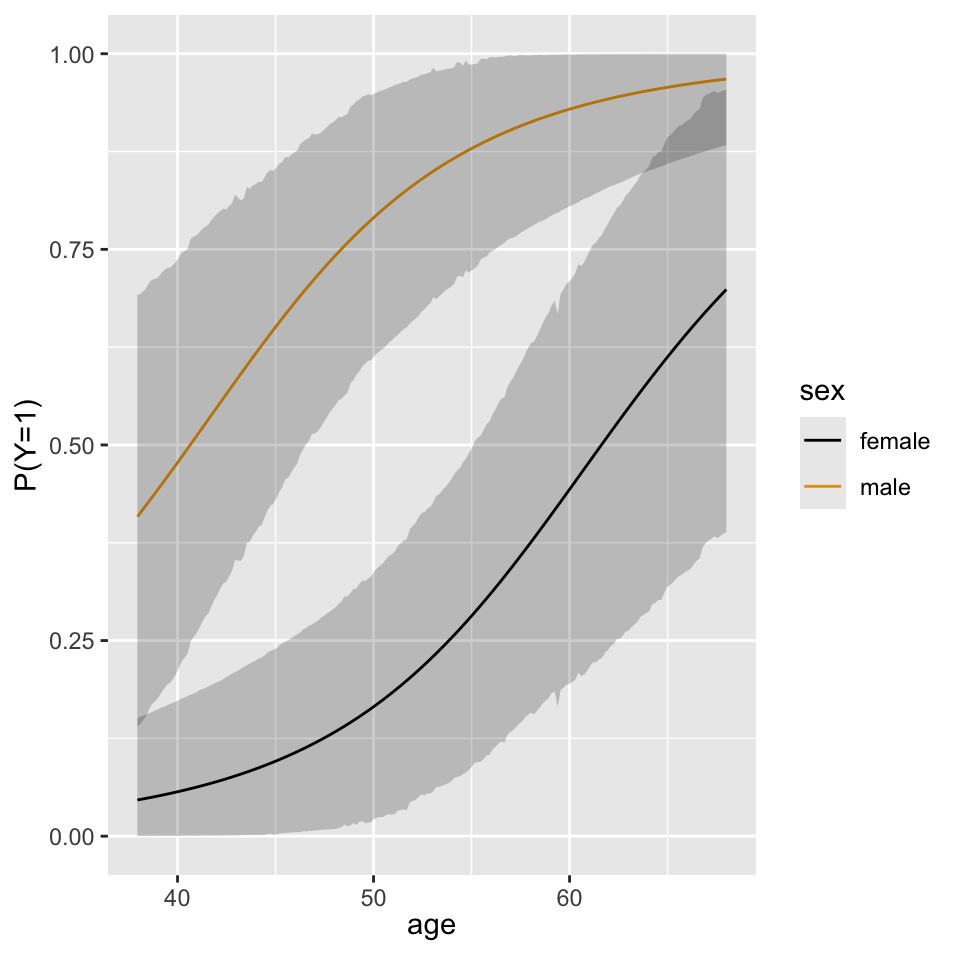

Code

# Frequentist
# variance-covariance for sex and age parameters
v <- vcov(flrm)[2:3,2:3]

# Sampling based parameter estimate correlation coefficient
f_cc <- v[1,2] / sqrt(v[1,1] * v[2,2])

# Bayesian
# Linear correlation between params from posterior 
draws <- f$draws[, c('sex=male', 'age')]
b_cc <- cor(draws)[1,2]

Using the code in the block above, we calculate the frequentist sampling-based parameter estimate correlation coefficient is 0.75 while the linear correlation between the posterior draws for the age and sex parameters is 0.77. Both models indicate a comparable amount of correlation between the parameters, though in difference senses (sampling data vs. sampling posterior distribution of parameters).

Code

P <- PostF(f, pr=TRUE)

 Original Name Short Name
 Intercept     a1        
 sex=male      b1        
 age           b2

Code

(p1 <- P(b1 > 0))   # post prob(sex has positive association with Y)

[1] 1

Code

(p2 <- P(b2 > 0))

[1] 0.9993

Code

(p3 <- P(b1 > 0 & b2 > 0))

[1] 0.9993

Code

(p4 <- P(b1 > 0 | b2 > 0))

[1] 1

The posterior probability that sex has a positive relationship with hospital death is estimated as \(\Pr(\beta_{sex} > 0)=1\) while the posterior probability that age has a positive relationship with hospital death is \(\Pr(\beta_{age} > 0)=0.9993\) and the probability of both events is \(\Pr(\beta_{sex} > 0 \cap \beta_{age} > 0) = 0.9993\). Even using somewhat skeptical priors centered around 0, male gender and increasing age are highly likely to be associated with the response.

As seen above, the MCMC algorithm used by blrm provides us with samples from the joint posterior distribution of \(\beta_{age}\) and \(\beta_{sex}\). Unlike frequentist intervals which require the log-likelihood to be approximately quadratic in form, there are no such restrictions placed on the posterior distribution, as it will always be proportional to the product of the likelihood density and the prior, regardless of the likelihood function that is used. In this specific example, we notice that the bivariate density is somewhat skewed — a characteristic that would likely lead to unequal tail coverage probabilities if a symmetric confidence interval is used.

Code

ggplot(as.data.frame(draws), aes(x=`sex=male`, y = age)) + 
  geom_hex() + 
  theme(legend.position="none")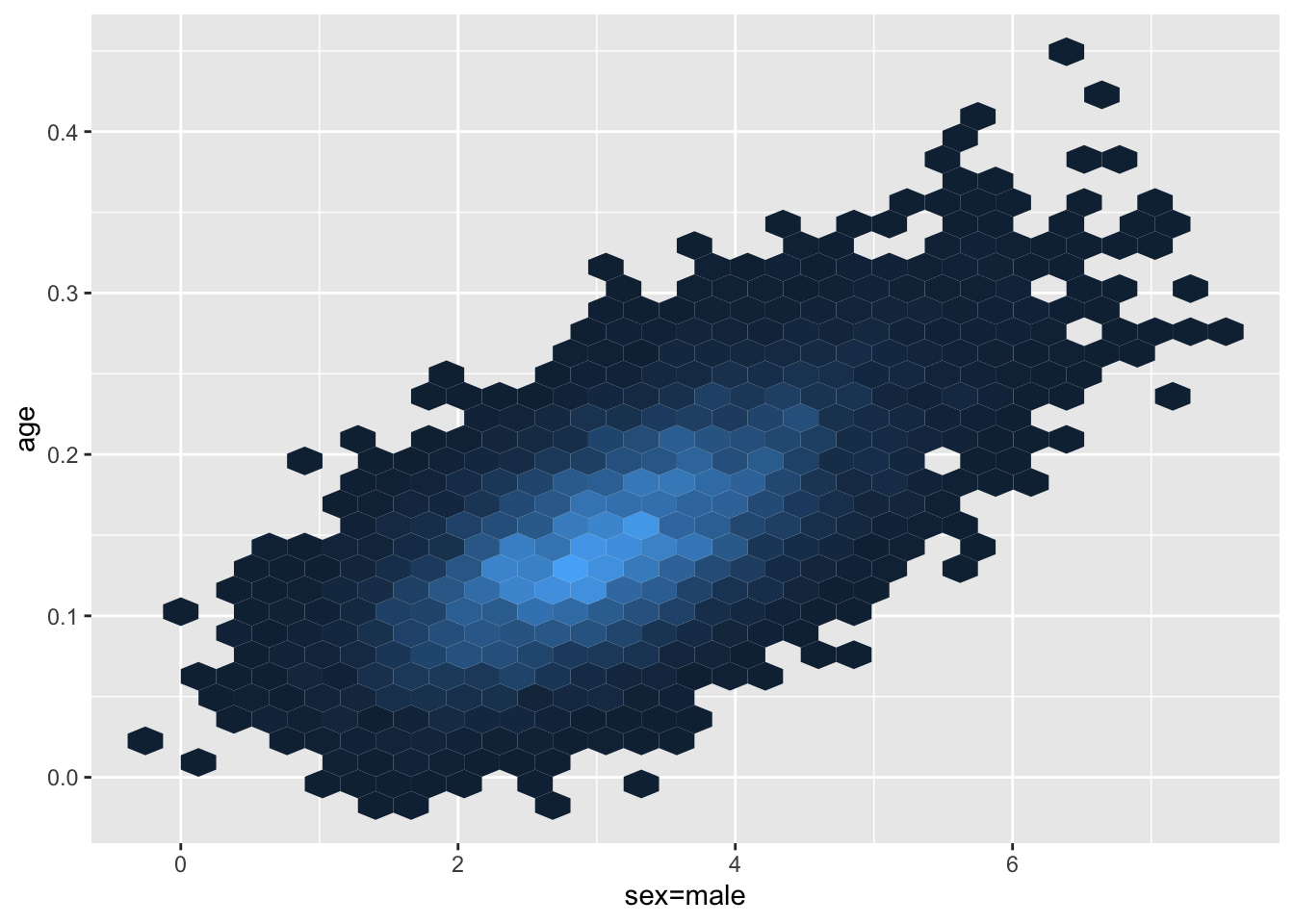

10.12 Study Questions

Section 10.1

Why can the relationship between X and the log odds possibly be linear?
Why can the relationship between X and the probability not possibly be linear over a wide range of X if X is powerful?
In the logistic model Prob\([Y=1 | X] = \frac{1}{1 + \exp(-X\beta)} = P\), what is the inverse transformation of \(P\) that “frees” \(X\beta\), both in mathematical form and interpreted using words?
A logistic model is used to relate treatment to the probability of patient response. X is coded 0 for treatment A, 1 for treatment B, and the model is Prob\([Y=1 |\) treatment\(]= \frac{1}{1+\exp[-(\beta_{0} + \beta_{1}X)]}\). What are the interpretations of \(\beta_{0}\) and \(\beta_{1}\) in this model? What is the interpretation of \(\exp(\beta_{1})\)?
What does the estimate of \(\beta\) optimize in the logistic model?
In OLS an \(F\) statistic involves the ratio between the explained sum of squares and an estimate of \(\sigma^2\). The numerator d.f. is the number of parameters being tested, and the denominator d.f. is the d.f. for error. Why do we always use \(\chi^2\) rather than \(F\) statistics with the logistic model? What denominator d.f. could you say a \(\chi^2\) statistic has?
Consider a logistic model logit\((Y=1 | X) = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2}\), where \(X_1\) is binary and \(X_2\) is continuous. List all of the assumptions made by this model.
A binary logistic model containing one variable (treatment, A vs. B) is fitted, resulting in \(\hat{\beta_{0}} = 0, \hat{\beta_{1}} = 1\), where the dummy variable in the model was I[treatment=B]. Compute the estimated B:A odds ratio, the odds of an event for patients on treatment B, and (to two decimal places) the probability of an event for patients on B.
What is the central appeal of the odds ratio?
Given the absence of interactions in a logistic model, which sort of subjects will show the maximum change in absolute risk when you vary any strong predictor?
Would binary logistic regression be a good method for estimating the probability than a response exceeds a certain threshold?

Section 10.2

What is the best basis for computing a confidence interval for a risk estimate?
If subect risks are not mostly between 0-0.2 and 0.8-1.0, what is the minimum sample size for fitting a binary logistic model?

Section 10.5

What is the best way to model non-additive effects of two continuous predictors?
The lowess nonparametric smoother, with outlier detection turned off, is an excellent way to depict how a continuous predictor \(X\) relates to a binary response \(Y\) (although splining the predictor in a binary logistic model may perform better). How would one modify the usual lowess plot to result in a graph that assesses the fit of a simple linear logistic model containing only this one predictor \(X\) as a linear effect?

Section 10.8

What are examples of high-information measures of predictive ability?
What is a measure of pure discrimination for the binary logistic model? What commonly used measure in medical diagnosis is this measure equivalent to?
Name something wrong with using the percent of correctly classified observations to quantify the accuracy of a logistic model.

Section 10.9

What is the best way to demonstrate the absolute predictive accuracy of a binary logistic model?

Austin, P. C., & Steyerberg, E. W. (2019). The Integrated Calibration Index (ICI) and related metrics for quantifying the calibration of logistic regression models. Statistics in Medicine, 38(21), 4051–4065. https://doi.org/10.1002/sim.8281

Carpenter, B., Gelman, A., Hoffman, M., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M., Guo, J., Li, P., & Riddell, A. (2017). Stan: A Probabilistic Programming Language. J Stat Software, 76(1), 1–32. https://doi.org/10.18637/jss.v076.i01

Cook, N. R. (2007). Use and misues of the receiver operating characteristic curve in risk prediction. Circ, 115, 928–935.

example of large change in predicted risk in cardiovascular disease with tiny change in ROC area;possible limits to c index when calibration is perfect;importance of calibration accuracy and changes in predicted risk when new variables are added

Pencina, M. J., D’Agostino, R. B., & Demler, O. V. (2012). Novel metrics for evaluating improvement in discrimination: Net reclassification and integrated discrimination improvement for normal variables and nested models. Stat Med, 31(2), 101–113. https://doi.org/10.1002/sim.4348

Pencina, M. J., D’Agostino Sr, R. B., D’Agostino Jr, R. B., & Vasan, R. S. (2008). Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Stat Med, 27, 157–172.

small differences in ROC area can still be very meaningful;example of insignificant test for difference in ROC areas with very significant results from new method;Yates’ discrimination slope;reclassification table;limiting version of this based on whether and amount by which probabilities rise for events and lower for non-events when compare new model to old;comparing two models;see letter to the editor by Van Calster and Van Huffel, Stat in Med 29:318-319, 2010 and by Cook and Paynter, Stat in Med 31:93-97, 2012

Pryor, D. B., Harrell, F. E., Lee, K. L., Califf, R. M., & Rosati, R. A. (1983). Estimating the likelihood of significant coronary artery disease. Am J Med, 75, 771–780.

Spanos, A., Harrell, F. E., & Durack, D. T. (1989). Differential diagnosis of acute meningitis: An analysis of the predictive value of initial observations. JAMA, 262, 2700–2707. https://doi.org/10.1001/jama.262.19.2700

Stan Development Team. (2020). Stan: A C++ Library for Probability and Sampling. https://cran.r-project.org/package=rstan

Tjur, T. (2009). Coefficients of determination in logistic regression models—A new proposal: The coefficient of discrimination. Am Statistician, 63(4), 366–372.

Wenger, T. L., Harrell, F. E., Brown, K. K., Lederman, S., & Strauss, H. C. (1984). Ventricular fibrillation following canine coronary reperfusion: Different outcomes with pentobarbital and α-chloralose. Can J Phys Pharm, 62, 224–228.